基于“计算思维+学单”的小学信息技术支架式教学
徐钢强
计算思维是信息技术学科核心素养的重要组成部分,其实质是个体运用计算机科学领域的思想方法,在形成问题解决方案的过程中所产生的一系列思维活动,这就表明计算思维的培养必须以具体教学为载体,渗透到学生的学习活动中。
小学信息技术教学中计算思维培养的现实矛盾
在重视计算思维培养的同时,但也存在计算思维“人人都喊,人人都做,人人低效”的困境。究其根本原因,是小学生认知水平的局限和计算思维高要求的脱节,使得计算思维培养缺乏深度,浮于形式。那应如何补齐小学生低认知水平和计算思维高要求之间的断层呢?笔者认为,问题的实质就是如何做到计算思维培养的“深入”和教学策略的“浅出”的统一。
现实矛盾呼唤支架式教学
1.支架式教学
支架式教学法是基于建构主义学习理论的一种以学习者为中心、以培养学生的问题解决能力和自主学习能力为目标的教学法。在教学中,一步步地为学生的学习提供适当的线索或提示,也就是支架,让学生通过这些支架一步步进行探究提升,逐渐解决学习中的问题,掌握所要学习的知识,提高问题解决能力。
2.基于学单的支架式教学的优势
学单指的是教师根据教学重难点和学生学情,针对某个环节或知识点设计的、用于引导学生逐步理解掌握该重难点的类似“脚手架”的表单。基于学单的支架式教学具有以下优势:形式灵活,可以针对某个知识点或思维点展开,让支架式教学更有针对性;促进学生自主学习建构,激发学习动力,引导学生思维的主动生发;形成思维梯度,化繁为简,对问题进行梯度分解,以“脚手架”方式为学生提供思维支撑。
基于“计算思维+学单”的小学信息技术支架式教学的探索
1.助力思维提升,实现计算思维的深度发生
小学生对课堂上的思维活动,往往参与的积极性很高,但是却缺乏必要的深度,只停留于浅层次的思维。这时,教师可针对某个思维点,设计由浅而深、具有梯度的学单作为支架,为学生的思维升发提供必要的支撑。
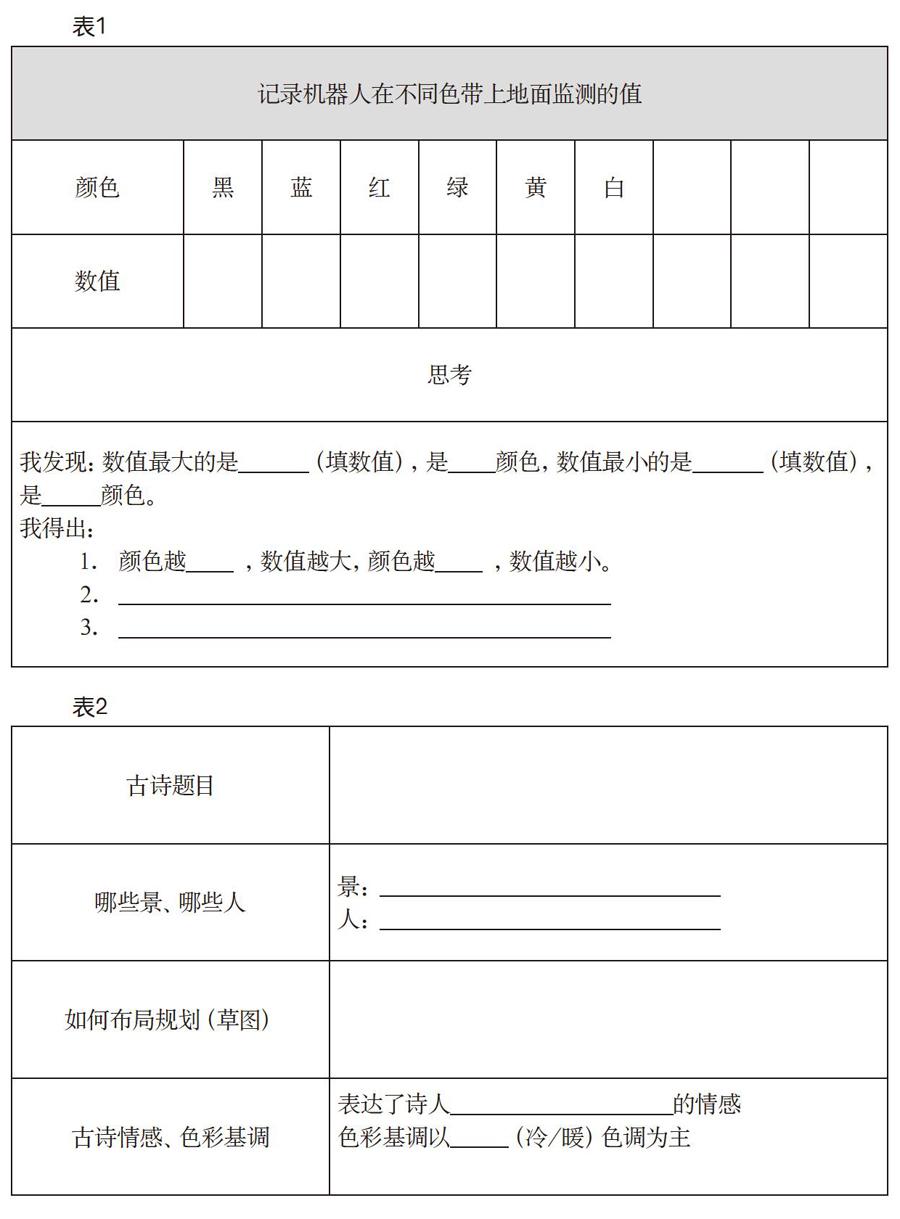
例如,在《机器人分辨颜色》一课中,让学生理解机器人分辨颜色的原理是难点。机器人为什么能够分辨不同的颜色是一个值得探究的问题,也是可以挖掘的一个思维点。为了引导学生实现计算思维的深度发生,笔者设计了如下页表1所示的学单。
学生以该学单为支架,通过实践得出各种颜色的灰度值,同时通过对这些数据的比较和分析,完成后续关于规律表单的填写,并最终得出对机器人分辨颜色的结论。
2.助力全局规划,实现计算思维链的完整重塑
对项目的分解规划,是计算思维的一个重要体现。但对全局的把握和规划意识是小学生的一个薄弱点,尤其是在面对一些需要全局把握的项目化任务时,这个矛盾尤为突出。
例如,《给古诗配画》是浙教版信息技术四年级上册画图与文字输入的综合任务。这节课的难度在于学生不仅要理解古诗的表层意思,而且要对整体的画面进行合理构思,更重要的是要理解古诗的深层意境,确定古诗配画的色彩基调。为了突破这个难点,笔者设计了如表2所示的学单,为学生思维提供支架。
在该学单中,笔者将学生的思维分解成一个思维链,一步步引导学生完成对全局的把控和规划,在这个过程中实现计算思维链的完整重塑。这在培养学生规划意识和全局意识的同时也培養了计算思维。
3.助力信息要素提炼,实现计算思维的结构化重组
计算思维从实质上讲是对原始问题进行分析、解构,最终建模实现自动化,但现实中的原始问题往往都是以非结构化表述呈现的劣构信息,这就要求要有更强的信息意识去提炼归纳其中的关键点,因此,从某种程度上讲,信息要素的提炼是计算思维的基础。但信息要素的提炼是小学生的弱项,所以基于信息提炼的学单就成为学生的学习支架。例如,在《表格的制作》一课中,笔者创设了为玉树贫困孩子挑选爱心书包的情境,呈现网上获取的劣构信息:a书包——红色面料图案超级飞侠、长30cm宽25cm高50cm、255元一个、外料PU皮里料尼龙、最大容量37.5L、双肩背带(带拉杆)、时尚可爱,省力;b书包——蓝色鲸鱼图案、192元一个、单肩背包45×20×45cm,容量40.5L、化纤材质、大方美观;c书包——98元一个、军绿色满天星图案、40×50×50cm,可装60L、尼龙材质、朴素耐用。同时提供如下页表3所示的学单。
在学单的支撑下,学生利用已有的材料,对其中的信息要素进行归纳,进而形成制作表格的各个要素,完成了数据的整理,为后续利用数据分析比较进而解决实际问题打下基础。
4.助力模式抽象,实现计算思维+算法的统一
算法是计算思维的重要体现。在实际教学中,尤其是编程教学中,困难的往往不是最终实现,而是对问题的分析建构和模式抽象。在图形化编程教学中,当涉及多角色多线程的程序设计时,学生往往无从下手,顾此失彼。
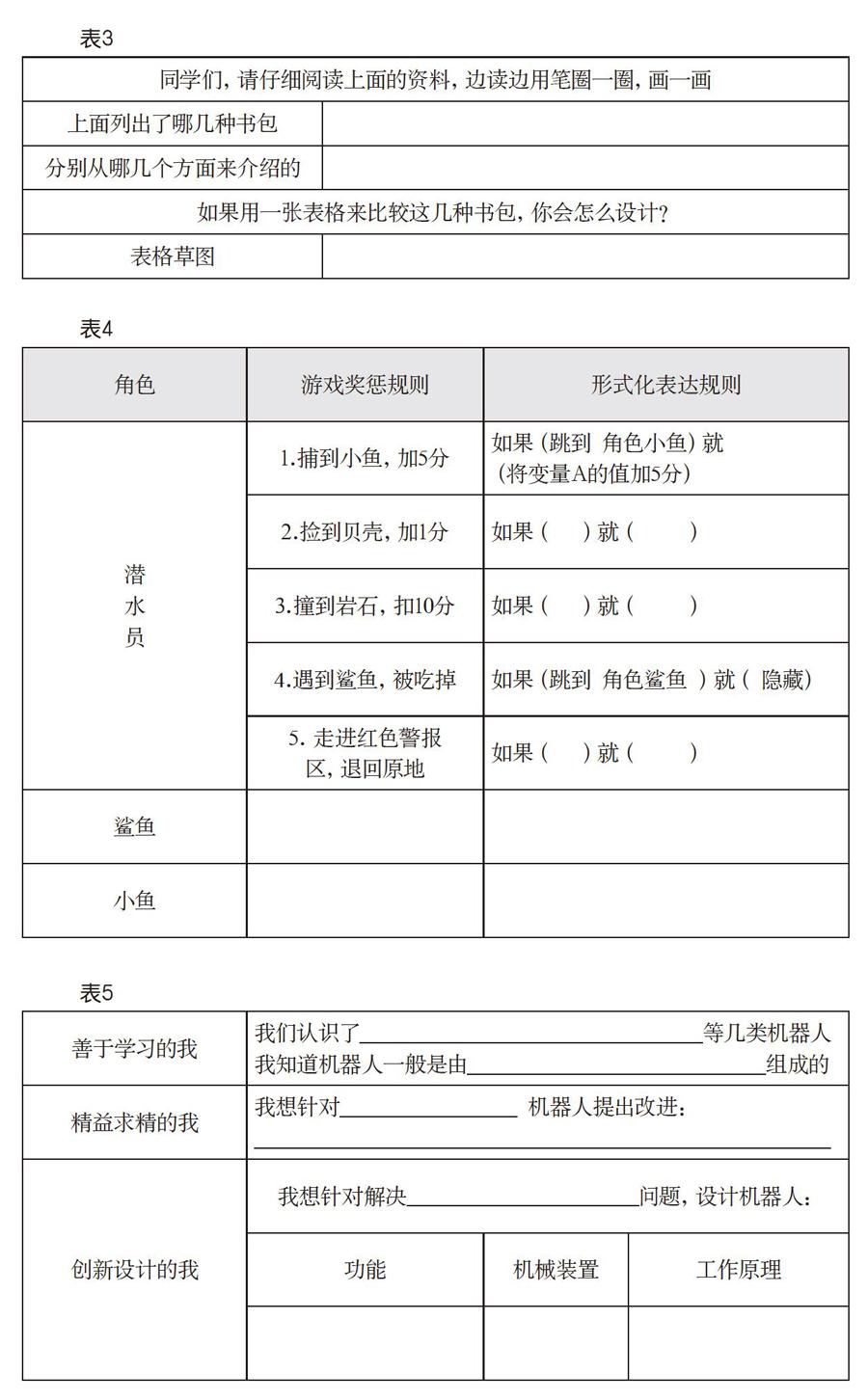
例如,浙教版信息技术六下《海底探险》一课,需要涉及潜水员、鲨鱼、贝壳、岩石等多个角色的互动,是完整运用算法思维解决实际问题的综合应用。难点是对各个角色的规则的结构化分解与抽象。为此,笔者设计了如表4所示的学单进行学习支撑。
结合学单,学生对游戏的各个角色进行规则提炼,进而形成形式表达,基本形成了整个游戏的算法设计,最终的程序实现也就水到渠成了。
5.助力课堂拓展,实现思维的广度发散
深度和广度是计算思维培养的两个维度。教学的目的,不仅仅是让学生学会知识和技能,更是要让学生学会学习,学会反思,学会举一反三,进而实现“不教而教”的目的。因此,学习的反思重构和发散拓展尤为重要。而思维的发散拓展是计算思维培养的创新维度,但却往往容易被忽视。
例如,在教学《我们身边的机器人》一课时,学生已经认识了许多机器人的功能、形态以及简单的原理,达成了本课的教学目标。但从培养思维广度方面看还不够,为此,笔者设计了如表5所示的学单。
在学单的支撑引导下,学生不仅对本课内容进行了重构,而且在不同思维层面上进行了发散拓展,以“在原来的基础上还能增加什么功能”为第一层面,以“请你根据实际需求设计一个机器人,并简单描述它的功能和工作原理”为第二层面,加深了对机器人原理的认识,激发了思维的创新。
学单是小学生认知水平短板和计算思维培养之间的纽带,它一方面是学生学习的支架,另一方面也是教师吃透教材,尊重学情、落实计算思维的手段。让学生在学单的支撑下,主动进行建构,收获成长的快乐,是支架式教学的精髓所在。

