基于灰色理论和时间序列模型预测棉花产量可行性研究

尹晓燕 王旭阳 史澳 何晓丰 王雪 刘云

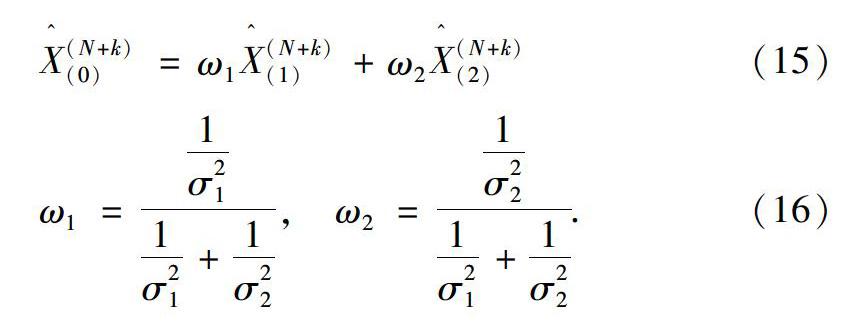
摘要：为了进一步提高新疆棉花产量的预测精度，运用GM模型与ARIMA模型对新疆棉花产量进行了预测，进而赋予合理权重建立了基于灰色理论和时间序列的组合预测模型对新疆棉花产量进行了预测。实证分析结果表明：组合模型的预测结果更加逼近于真实数据，预测精确度较单一预测模型的结果准确性更高、误差更小。因此， GM模型与ARIMA模型组合预测新疆棉花产量是可行的。

关键词：灰色理论;时间序列;组合模型;棉花产量;预测

中图分类号：S562

文献标识码：A

文章编号：2095-3143（2021）01-0015-07

DOI：10.3969/j.issn.2095-3143.2021.01.003

Abstract：In order to improve the forecast precision of Xinjiang cotton yield， the GM model and ARIMA model are used to predict Xinjiang cotton yield， the combination forecasting model based on grey theory and time series was established to predict the cotton yield in Xinjiang. The results of empirical analysis showed that the forecasting accuracy of the combined model is higher and the error is smaller than that of the single model. Therefore， it is feasible to combin the GM model and the ARIMA model to forecast cotton yield in Xinjiang.

Key words：Grey theory; Time series; Combination model; Cotton yield; Forest

新疆维吾尔自治区是我国主要的植棉区之一，同时也是我国最大的优质棉和唯一的长绒棉生产基地。在新疆农业中，棉花产业占居主导地位，其产量的变动对棉花行业相关从业者的经营和发展有重大的影响。棉花产业的健康发展对新疆农业及纺织工业的发展具有极其重要的意义[1]。相对于一熟旱地作物，棉花生长周期长，受自然环境的影响大。长期以来，棉花产量面临较大的风险，波动频繁，需要进行产量预测，以改变管理措施和调控市场。

近年来，基于不同的研究对象众多学者运用不同的方法对新疆棉花产量进行了预测。目前学者研究的热点是系统分析法，主要包括灰色理论预测法、人工神经网络预测法、时间序列预测法以及系统动力学法等。这些方法对平稳的时间序列取得较好的预测效果，得出了一系列重要的结论[2]。为了能够合理的利用各种预测模型的优点，Bates，等[3]将不同的预测模型进行适当的组合，于1969年提出了组合预测的方法，该方法能够综合利用各种预测模型提供的信息，尽可能地提高预测的精度。近年来已有许多对组合预测模型得到了推广。邢棉[4]提出了灰色神经网络组合模型，为较复杂的季节性预测问题，提供了一种新的有效的方法，并对电网供电量进行了预测。朱辉[5]运用了灰色预测模型，对新疆生产建设兵团棉花产量进行了预测，得到了精确度更高的预测值。陈黎明，等[6]运用灰色预测和回归模型建立组合预测模型对GDP统计数据质量进行了评估研究。单锐，等[7]为了更加精确的预测出人均GDP，采用了ARIMA模型与GM模型的组合模型，结果显示组合预测结果更加接近于真实值。佟长福，等[2]为了减少随机性，提出了基于小波分析理论的农业需水量组合预测模型。李晓彤，等[8]通过建立灰色模型和ARIMA-GARCH模型的组合模型对我国的股票市场进行了分析。张利平，等[3]通过建立六种时间序列组合模型并结合它们的优点，使其拟合及预测效果达到最优。为了对棉花的产量进行动态、科学、精准地预测，作者运用灰色理论与ARIMA模型对新疆棉花产量进行预测，运用相关统计软件分析得出单一灰色GM（1， 1）模型与ARIMA模型的预测结果，之后结合二者各自的优点赋予合理权重建立基于灰色理论和时间序列的组合预测模型，以期提高棉花产量预测的精度，为政府及棉花相关从业者制定合理的生产、销售、储存和加工等产销策略提供参考与借鉴。

1灰色时间序列组合预测模型

1.1 GM（1， 1）模型

灰色预测是一种对具有不确定因素的系统进行预测的方法，能有效解决数据少、序列的完整性及可靠性低的问题。GM（1， 1）模型是一种较为常用的灰色模型，GM（1， 1）预测模型的建立实质上就是对原始数据序列作一次累加生成，使生成数据序列呈显出一定规律，然后通过建立微分方程模型，求得拟合曲线，进而对系統进行预测。该模型构建思路如下。

1.2 ARMIA模型

ARIMA模型（自回归积分滑动平均模型）是一种根据系统观察得到的初始时间序列数据，通过曲线拟合和参数估计建立数学模型的理论和方法。ARIMA模型认为依照时间顺序进行排列的所有观测值之间都具有自相关性，这种自相关性延续了变量的发展趋势。若将这种自相关性用定量的方法描述，就可以依据时间序列的过去值预测其将来值。该模型构建思路如下。

（1）序列预处理：原始时间序列经过预处理，可以被识别为平稳非白噪声序列，就能够利用模型对该数据序列进行建模。

（2）模型识别：由给出的序列样本，根据样本自相关系数和偏自相关系数的性质，选择阶数适当的ARMA（p， q）模型进行拟合。

（3）参数估计：根据识别的模型及阶数，对模型进行参数估计和显著性检验。

（4）模型的构建：记原始时间序列数据为at（t=1，2，3，...，n），記at的秩为Rt=R（at），考虑变量对（t，Rt）（t=1，2，3，...，n）的Spearman的相关系数qs，则有（14）数据。

（5）平稳性检验：假设H0为平稳序列，H1为非平稳序列。对于显著水平a，由时间序列at计算（t，Rt）的Spearman秩相关系数qs，若T>ta2（n-2），则拒绝H0，认为序列非平稳。且当qs>0时，认为序列有下降趋势。又当T>ta2（n-2）时，接受H0，可以认为序列是平稳序列。

1.3组合预测模型

灰色模型是通过对原始数据加工处理来弱化随机性的，若数据存在较大的波动性，预测出来的结果可能会存在较大误差。ARIMA模型对于预测的模型比较理想，要求时序数据是稳定的，或者是进行差分后是稳定的，往往需要对数据进行预处理，导致预测的精度不够准确。单一的预测模型均存在一定的局限性，很难把握预测结果的准确性，从而使得误差较大。组合模型可以通过对各个预测模型加权平均，把单一预测模型的优点集合起来，形成预测精度更高的预测模型，可以大大减小误差，使得结果更加准确。

设原始序列的为X（0），预测序列为X^（0），观测样本数列为N，预测样本数为k，组合模型为（15），其中ω1，ω2的公式为（16）[4]。

式中：X^（N+k）（0）表示组合模型的k个预测值，X^（N+k）（1）表示灰色模型的k个预测值，X^（n+k）（2）表示ARIMA模型的k个预测值。ω1，ω2分别表示灰色模型、ARIMA预测模型的权重，σ1，σ2分别表示灰色模型、ARIMA预测模型的标准差。

检测结果表明，该组合预测方法优于单一预测方法，由此可得最优的组合预测模型。

2实证分析

选取2005～2019年的《新疆统计年鉴》中新疆维吾尔自治区棉花产量（单位为万吨）年度数据为研究对象，对棉花产量进行短期预测。

2.1 GM（1， 1）预测模型

按照GM（1， 1）的模型求解思路，建立传统GM（1， 1）模型，得到时间响应公式（17）。

利用Matlab软件求解GM（1， 1）模型，将新疆历年棉花产量作为训练数据，预测值与真实值的曲线拟合结果如图1所示。

一般情况，如果绝对误差百分比MAPE≤10%，同时远点误差小于2%时可以认定研究结果满足精度的要求。由模型拟合结果可得：MAPE=0.0764SymbolcB@

0.1认为模型精度误差满足要求。后验差比值C=0.2828<0.35，小误差概率p=1>0.95，认为精度检验合格。综上可知，本次GM（1， 1）灰色预测模型精度检验合格。模型精度等级为1级，模型拟合结果良好，建立的模型所得的预测值误差较小，其模型方程为（18）。将数据代入公式（18）中，可预测出棉花近几年的总产量，具体预测数据见表2。

2.2时间序列预测模型

ARIMA模型要求序列是平稳序列，因此要对数据进行平稳性分析。对样本数据进行ADF检验，发现原始序列是非平稳序列，经二阶差分后的P值<5%，在5%的显著性水平下是平稳序列。棉花产量序列经二阶差分后的自相关图ACF和偏自相关图PACF，如图1所示。

由图2也可以看出，二阶差分后，数据逐步趋于平稳，且满足置信区间，故差分次数d=2。差分后的序列可以通过自相关图和偏自相关图初步确定p和q的值，由图2可知，延迟5阶后，ACF和PACF均落在二倍标准差范围内，因此该数据序列满足ARIMA（5，2，1）模型。

2.3组合预测模型

对于上述两种单一预测模型的预测精度不高、数据波动较大等问题，若结合以上两种单一预测模型的特征，构建组合预测模型，经计算可得，GM（1，1）模型与ARIMA模型的组合权重系数分别为0.46497和0.53503。预测值与真实值的具体数据见表2。

基于灰色预测模型与ARIMA模型得组合预测模型，较好地结合了两种单一模型的优点，能够有效地拟合非线性波动及非线性增长趋势。从表2可以看出，组合预测模型的平均相对误差（MAPE）小于GM（1，1）模型与ARIMA模型这两种单一预测模型。说明组合预测模型有较高的预测精度，取得很好的预测效果，预测精度较两种单一预测模型有了很大的提高，实证分析结果表明该方法是有效和实用的，灰色预测模型与ARIMA模型的组合预测模型可以为相关从业者科学准确地预测新疆棉花产量提供依据和实践参考。

3结论

单独采用灰色理论预测模型和时间序列模型进行预测时，由于各个单一预测模型自身条件的限制，不能全面准确地掌握原始数据的信息，影响预测结果的准确性。而通过加权组合方式对两个单一预测模型进行组合，获到的组合预测模型弥补了两种单一预测模型自身的不足。本文基于灰色GM（1， 1）模型与时间序列ARIMA模型，通过加权组合方式将两种单一模型很好地融合在一起，并选取2005～2019年的新疆维吾尔自治区棉花产量年度数据为研究对象，对棉花产量进行了短期预测。实证分析结果表明组合模型预测的精度和稳定性高于单项预测模型。因此，这种组合预测模型用于棉花产量预测是有效可行的。这为复杂性时间序列的建模和预测提供了切实可行的方法。

参考文献

[1]李娟丽， 许英. 基于ARIMA模型的新疆棉花产量的预测分析[J]. 教育现代化，2018，5（17）：149-150.

[2]佟长福， 史海滨， 包小庆， 等. 基于小波分析理论组合模型的农业需水量预测[J]. 农业工程学报，2011，27（05）：93-98.

[3]张利平， 于贞杰， 张建华， 等. 六种时间序列组合建模方案在卫生费用趋势拟合中的应用研究[J]. 中国卫生经济， 2015，34（08）：56-58.

[4]邢棉. 季节性预测的组合灰色神经网络模型研究[J]. 系统工程理论与实践，2001， 21（01）：31-35.

[5]朱辉.GM（1， 1）模型在新疆生产建设兵团棉花总产量预测中的应用[J]. 安徽农业科学，2008（20）：8399-8400.

[6]陈黎明， 傅珊. 基于组合预测模型的GDP统计数据质量评估研究[J]. 统计与决策，2013（08）：8-11.

[7]单锐， 王淑花， 高东莲， 等. 基于时间序列模型与灰色模型的组合预测模型的研究[J]. 燕山大学学报，2012，36（01）：79-83.

[8]李晓彤. 基于小波分析的灰色模型与ARMA-GARCH模型的组合预测[D]. 济南： 山东大学，2018.

[9]杨中旭. 棉花产量的Fuzzy预测法[J]. 江西棉花，1995，17（01）：18-21.

[10]邓聚龙. 灰色系统理论教程[M]. 武汉： 华中理工大学出版社， 1990.