干式螺杆压缩机壳体水夹层换热性能分析
吴 强,袁玮玮,王存华,高培文,卢 笋,孙 远
(1.中国石油天然气集团有限公司独山子石化分公司,新疆独山子 833699;2.中国船舶集团有限公司第七一一研究所,上海 200072)
1 引言
在某些工况下,螺杆压缩机排气温度比较高,由于壳体内壁面为双孔结构且各处温度不同,整个表面的热膨胀量不均匀,由此导致转子与壳体内壁面之间的间隙发生变化,间隙变小的地方转子擦缸的风险增大,间隙变大的地方泄漏损失增大以致主机效率降低。针对此问题,常常采用水夹层壳体,即在气缸外表面还存在一层壳体,中间通入冷却水进行换热,从而降低气缸内壁面温度至设计范围。
针对带有水夹层壳体的干式螺杆压缩机,腔体内的温度控制是决定压缩机可靠性的关键要素,由于螺杆压缩机内部流动比较复杂,很难直接对螺杆压缩机水夹层壳体内壁面的冷却效果进行定量计算,因此,本文将此问题分解为2部分:(1)等熵压缩过程中壳体内壁面温度分布计算;(2)冷却水对壳体内壁面冷却效果计算。之后将2块内容结合,可近似地得到螺杆压缩机壳体内壁面在水夹层冷却作用下的温度分布。
2 等熵压缩过程中壳体内壁面温度分布计算
2.1 压力关系
假设螺杆压缩机中气体为理想气体,不考虑泄漏,压缩过程为等熵压缩。
根据工程热力学相关原理[1],压缩过程中任一时刻m满足
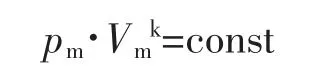
式中 pm——任一时刻m的压力
Vm——任一时刻m的齿间容积
k——气体的等熵指数
已知螺杆压缩机进气压力ps,吸气容积Vs,进气温度Ts,则
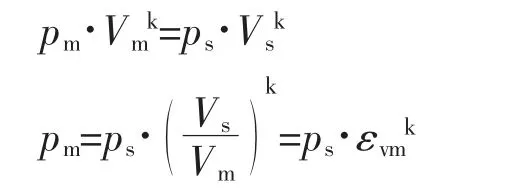
式中 εvm——任一时刻m的内容积比
2.2 温度关系
由理想气体状态方程
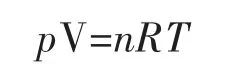
则有

式中 Tm——任一时刻m的温度
2.3 压缩过程中阴阳转子转角与内容积比的关系
参考螺杆压缩机相关教材[2],螺杆压缩机的压缩过程通常分为2个阶段:第一阶段从转子齿间容积开始减少,至阴阳转子的一对齿间容积间形成形状和长度不变的接触线时为止(只有当螺杆压缩机在压力比较小时,压缩过程终止于此阶段);第二阶段从第一阶段结束,到阳转子转过一个阳转子扭转角τ1z时为止。
对齿间容积的变化进行研究,如图1所示,当阴转子齿1′转到即将侵占阳转子齿1后的齿间面积A01位置时,即为压缩开始点,也是齿间容积减少的起点,相应的阳转子齿1的齿顶径线与O1O2连线的夹角为β。规定处于这一位置时的阳转子转角为零,即φ1=0。
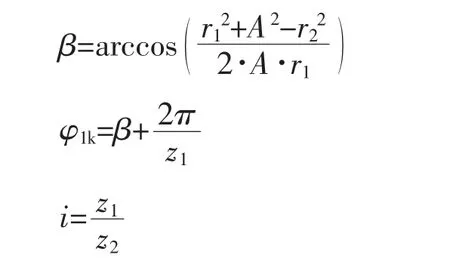
式中 r1——阳转子外圆半径
A——转子中心距
r2——阴转子外圆半径
φ1k——第一阶段结束时的阳转子转角
z1——阳转子齿数
i——齿数比
z2——阴转子齿数
则在第一阶段(0≤φ1≤φ1k),螺杆压缩机内容积比εv与阳转子转角φ1之间的关系为
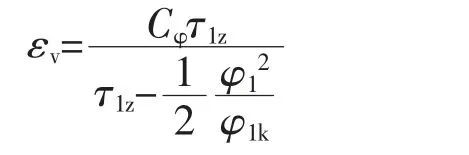
式中 Cφ——扭角系数
τ1z——阳转子扭转角
在第二阶段(φ1k≤φ1≤τ1z),内容积比εv与阳转子转角φ1之间的关系为
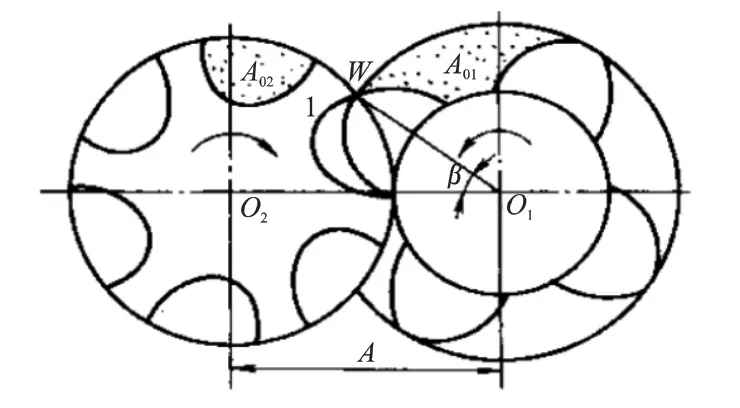
图1 基元容积开始减少时的转子位置
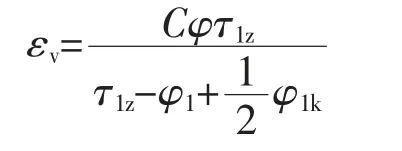
令阳转子转角φ1=0时,阴转子转角φ2=0,由阴阳转子啮合关系可得到内容积比εv与阴转子转角φ2之间的关系。
在第一阶段(0≤φ2≤iφ1k),内容积比εv与阴转子转角φ2之间的关系为
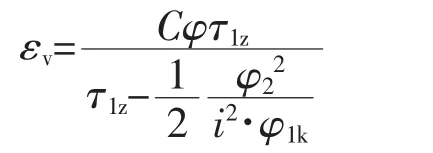
第二阶段(iφ1k≤φ2≤iτ1z),内容积比εv与阴转子转角φ2之间的关系为
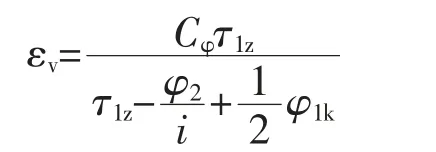
2.4 轴向吸气角
阳转子轴向吸气角α1s为
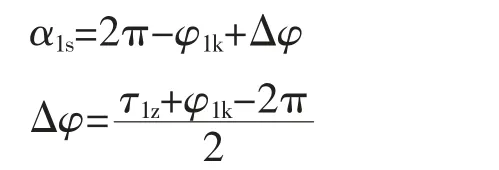
式中 Δφ——阳转子吸气角修正值
阴转子轴向吸气角α2s为
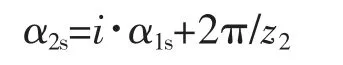
2.5 轴向排气角
阳转子轴向排气角α1d为
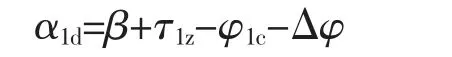
式中 φ1c——阳转子内压缩转角
阴转子的轴向排气角α2d为
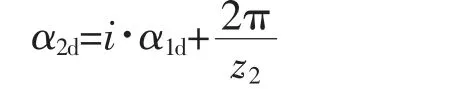
2.6 阴阳转子角度与温度的关系
由以上推导,可得到进气端面上阴阳转子角度与温度的关系。
进气端面上阳转子角度α1与温度T(α1)的关系为

进气端面上阴转子角度α2与温度T(α2)的关系为

2.7 壳体内壁面温度
根据转子螺旋特征,沿螺旋线温度值相同,从而可将三维问题转换为二维问题,根据进气端面上的温度分布即可得到壳体内壁面温度分布。
在转子旋转过程中,壳体上任一点的温度为周期性变化,由螺旋线方程计算得到该点在进气端面上对应的角度为θ。若该点在阳转子侧,则该点温度的变化区间为;若该点在阴转子侧,则该点的变化区间为。根据温度变化区间,即可得到壳体上任一点的温度瞬态变化曲线。例如,对排气端面上各点的温度值进行计算,得到各点的温度变化曲线如图2所示。
对温度变化曲线求平均值,即可得到稳态温度值。
阳转子侧壳体任一点的稳态温度值Tv1为
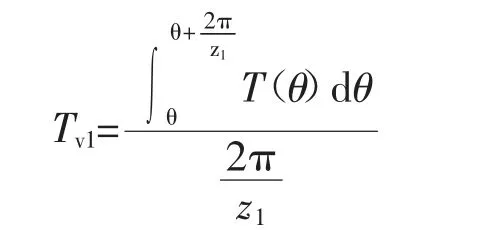
阴转子侧壳体任一点的稳态温度值Tv2为
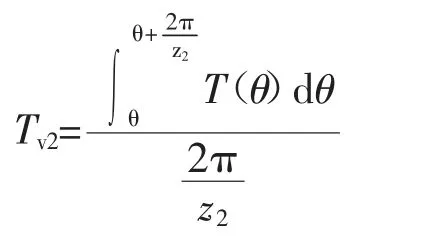
由此得到等熵压缩过程中壳体内壁面温度稳态分布如图3所示。
3 冷却水对壳体内壁面冷却效果计算
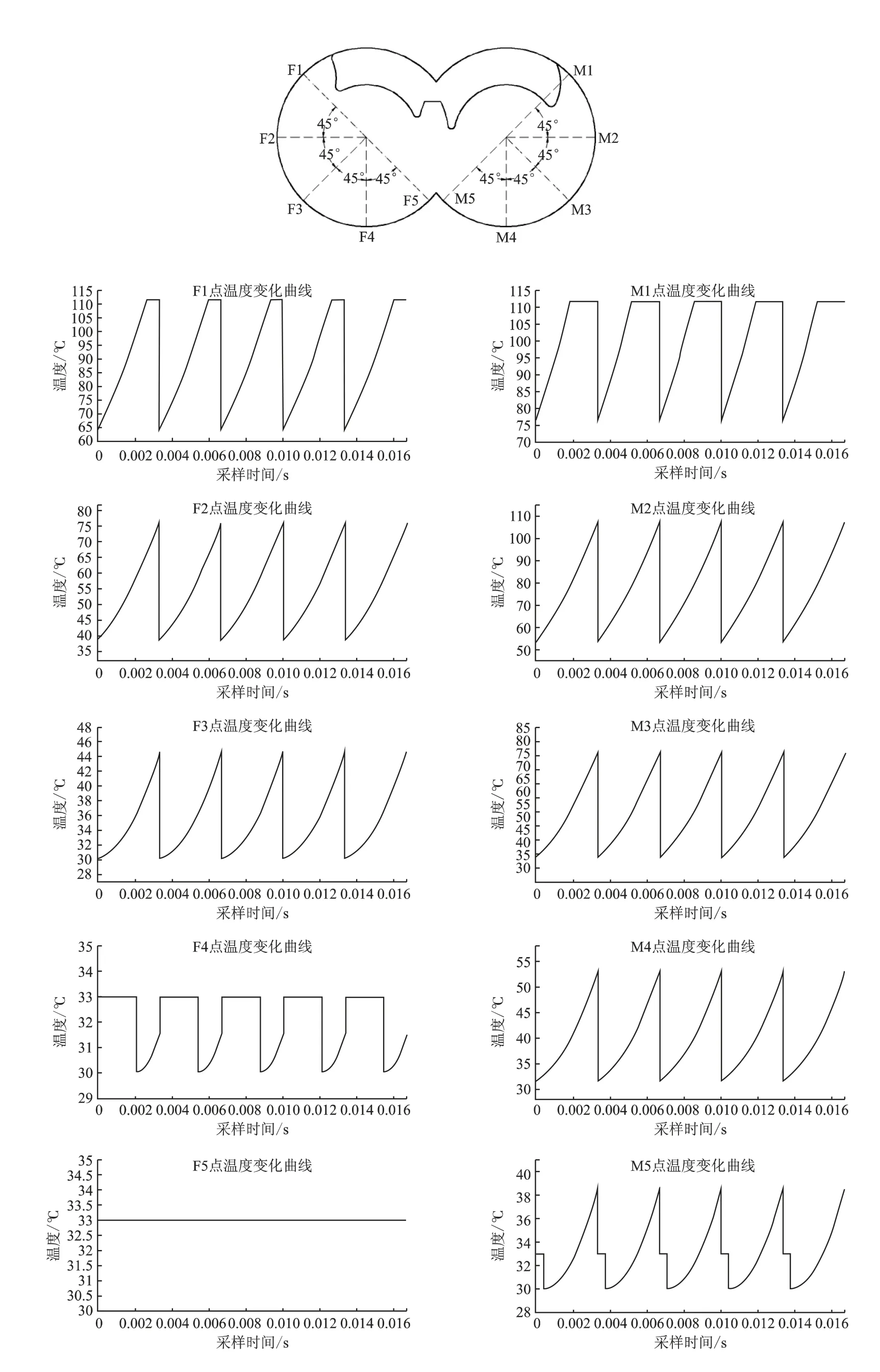
图2 排气端面各点温度瞬态变化曲线
由于螺杆压缩机壳体结构不规则,流体在压缩机中的流动情况亦较为复杂,很难对此传热学问题计算得到解析解。因此,本文对其进行简化,取角度为dγ、轴向长度为l的壳体微元,如图4阴影部分所示,由于角度很小,可将此微元近似为平板,假设流体流经平板时温度保持恒定,忽略边界层效应,不考虑热辐射。
根据传热学相关原理[3],流体外掠全板长等温平板层流换热的关联式为
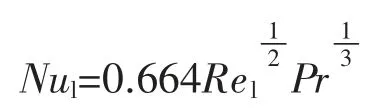
流体外掠全板长等温平板湍流换热的关联式为
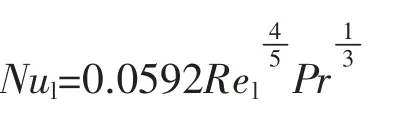
式中 Nul——努塞尔数
Rel——雷诺数
Pr——普朗特数
则平板的表面传热系数h及换热量φ为
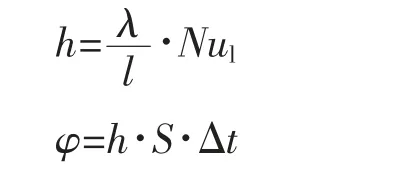
式中 λ——导热系数
l——平板长度
S——流体流通面积
Δt——换热温差
当稳态时,壳体的温度保持不变,即气体与壳体的换热量,等于水与壳体的换热量。
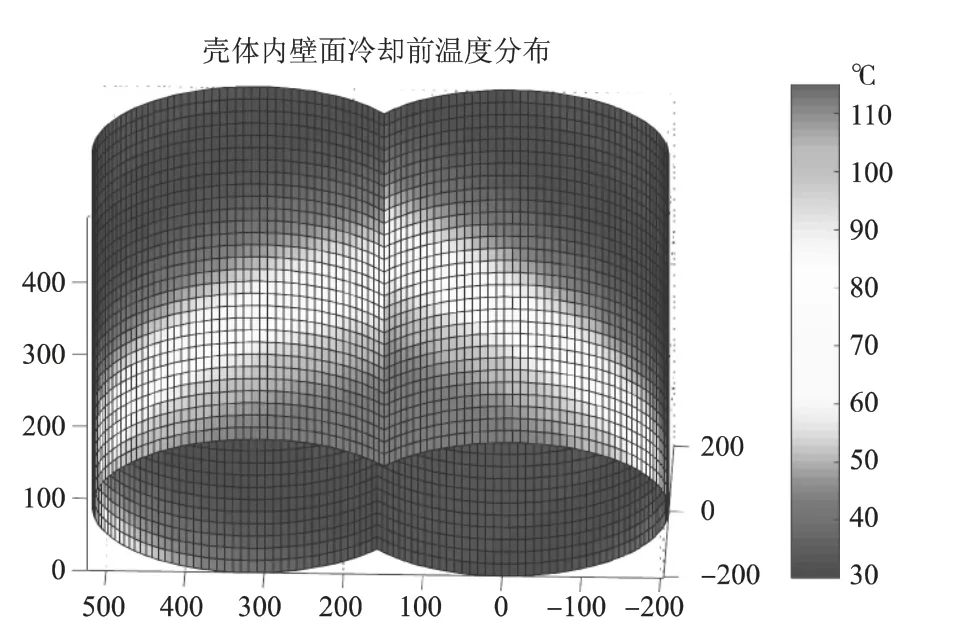
图3 壳体内壁面冷却前稳态温度分布
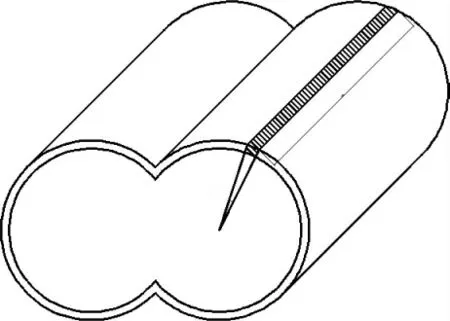
图4 壳体简化模型
若某项目给定输入参数如表1所示。
在冷却水条件恒定的情况下,改变介质气温度tg,调取NIST refprop介质气相关物性参数:密度ρ、运动粘度υ、普朗特数Pr、导热系数λ,计算稳态时壳体与介质气温差Δtg,得到tg与Δtg之间的关系曲线如图5所示。
将等熵压缩过程中壳体内壁面稳态温度分布减去水夹层换热后的冷却温差,即可得到壳体内壁面冷却后的温度分布,如图6所示。
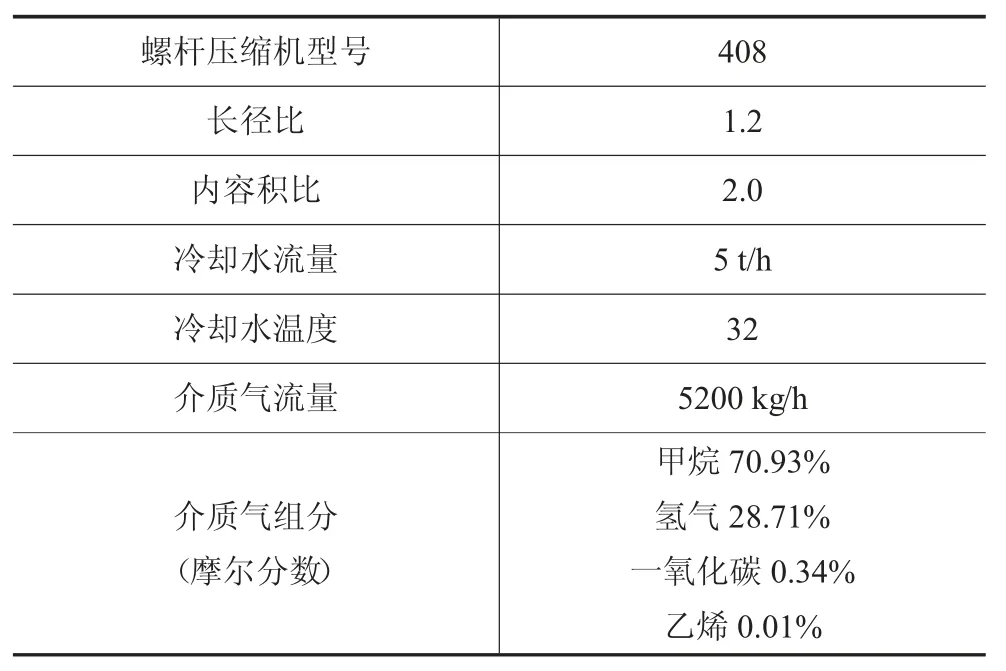
表1 输入参数
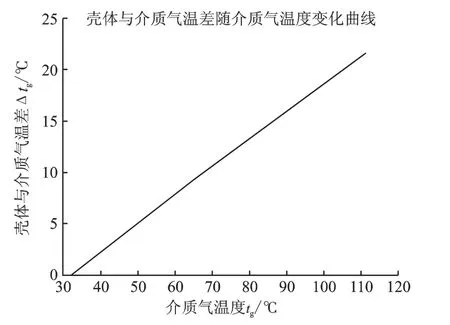
图5 壳体与介质气温差随介质气温度变化曲线
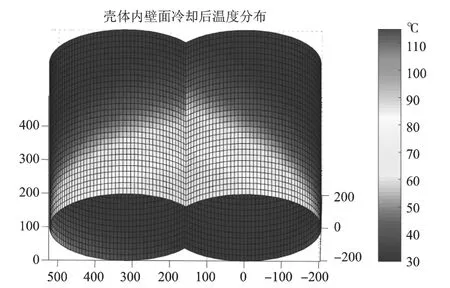
图6 壳体内壁面冷却后温度分布
由此,即得到螺杆压缩机壳体内壁面任一点在水夹层冷却前后的温度,例如对图7排气端面上各点沿轴线(由排气端面到进气端面)冷却前后的温度分布进行计算,计算结果如图7所示。
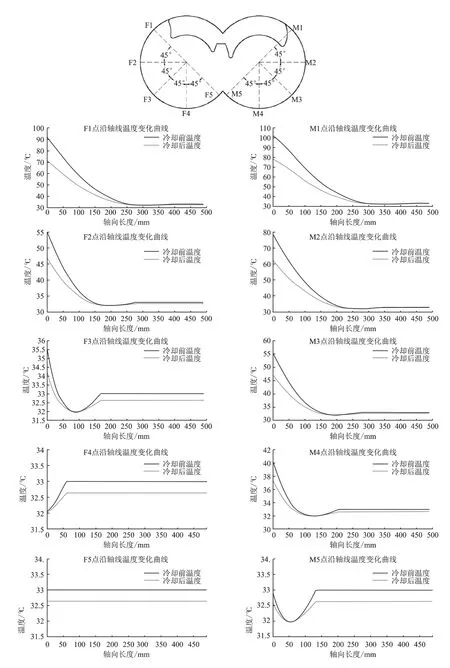
图7 排气端面上各点沿轴线温度分布
4 结论
针对螺杆压缩机水夹层对气缸内壁面冷却效果的定量计算问题,本文主要做了以下工作:
(1)推导了等熵压缩过程中壳体内壁面温度分布计算方法,得到壳体内壁面瞬态及稳态温度分布;
(2)建立了冷却水对壳体内壁面的换热计算模型,得到了在不同温度下水夹层冷却效果变化曲线;
(3)通过上述两部分内容结合,得到壳体内壁面在水夹层冷却作用下的温度分布,从而为水夹层设计、间隙设计提供参考。

