1979-2019年北半球极端高温的变化主导因子分析
王天奇,王鹏凯
(1.华风气象传媒集团有限责任公司,北京 100081;2.福山区气象局,山东 烟台 265500)
1 引言
在全世界范围内,无论是从强度、种类还是范围指标来看, 中国都是受到极端气候事件以及气象灾害影响最严重的国家之一。 1984-2013年,气象灾害平均每年给中国造成的直接经济损失高达1888 亿元[1],而高温就是这些气象灾害中常见的一种。 在人口密度增大、人口流动性大幅增加等因素的影响下,中国受极端天气事件的影响将会越来越大[2]。 因此,深入研究极端高温的变化特征及影响因子, 除可以了解相关气象要素的演变规律外, 还可以提升预测极端气候事件的准确性, 并且在国家防灾减灾体系建设及相关政策制定中发挥重要的作用, 有助于降低高温灾害带来的人员伤亡和财产损失。
本文在探究主导气候因子对关键区域高温频次影响的同时, 也定量分析出均值和标准差变化在这些影响中的贡献程度, 在1979-2019年北半球极端高温事件变化特征的归因分析上会有更加客观的判断。
2 资料与方法
2.1 气温统计参数与温度极值

正态分布曲线峰值即平均气温所在位置, 当气温平均值变化时,该曲线会发生左右平移,平均温度升高(降低),则曲线向右(左)平移。 σ 表示数据的离散度,当σ 变大时数据的离散度就越大,当σ 变小时数据的离散度也相应变小, 从正态分布曲线的形状上看,σ 越大,曲线越扁平,反之,σ 越小,曲线越瘦高。
多个研究在假设温度分布为高斯分布的前提下讨论均值变化和变率变化对EHTE 的影响。 Weaver等人提出全球和北美极端高温事件 (Extreme High Temperature Event,EHTE)的增长主要是由于平均温度的变化[3]。Su和 Dong 指出,中国 EHTE 未来变化是由平均温度变化决定的[4]。 相比之下,Schar 等人强调欧洲EHTE 的可变性变化的关键作用[5]。 Argueso 等人得出的结论是, 均值变化和变率变化的相对作用表现出区域特征, 并且均值变化控制着全球未来EHTE 变化的大部分[6]。
2.2 再分析资料ERA5
本文所用的资料主要是ERA5 再分析数据集中1979-2019年北半球2 m 温度数据和高度场数据,空间分辨率为 1.5°×1.5°, 文中所指北半球为赤道以北地区,夏季为6-8月。
2.3 海表温度资料
海表面温度资料是 Extended Reconstructed Sea Surface Temperature (ERSST) v5 的海表温度数据集,由美国国家海洋和大气管理局(NOAA)提供,本文所用的资料主要是1979-2019年夏季(6-8月)的海表温度,水平分辨率为 2°×2°。
2.4 经验正交函数(EOF)分解
EOF分析可以提取出矩阵数据的主要特征量,也可以分析其结构特征。
原理与算法:
1.选择要分析的数据并对数据进行预处理,通常为距平处理。 得到一个数据矩阵Xm×n
2. 计算数据矩阵和它转置矩阵的交叉积可以得到方阵

3. 计算方阵 C 的特征根 (λ1,...,λm)和特征向量Vm×m,二者满足

其中∧是m×m 维对角阵。
2.5 相关分析
相关系数可以表示两个数据的线性相关度。 在这里用 r 来表示相关系数。数据x和y 之间的相关系数r 为:

r 的值在-1-1 之间。 r 值离 0 越近,代表两个数据的相关关系越弱。 当r>0 代表两者有正相关关系,反之有负相关关系。 r 的显著性水平检验可用 t 检验法。
2.6 高温的定义
本文中高温为绝对阈值定义, 即绝对阈值高温为日最高气温≥35 ℃。
3 绝对阈值高温日数的时空特征
为分析北半球1979-2019年夏季高温日数变化的时空分布特征,对高温日数进行EOF分解。 从35℃高温看,第一模态方差贡献率为29.7 %,可以反映高温日数变化的主要特征。 北美中南部、非洲北部、中东地区表现为一致型的正值分布特征, 大值区主要位于非洲东北部地区, 说明该地区夏季高温日数的变化幅度最大(图1)。 对应的时间系数表明北半球夏季高温日数有明显的上升趋势, 其最大值在2019年,最小值在1984年。2000年以后,第一模态时间系数大部分都为正值,表明2000年以后北半球高温日数相对2000年以前呈现上升趋势。 第二模态方差贡献率是9.8 %,反应出北美洲南部、中东地区和非洲北部、印度反向变化(图2)。

图1 35 ℃高温日数EOF 空间分布

图2 35 ℃高温日数EOF 对应的时间系数
北半球35 ℃高温日数EOF分析中前两个模态分别表现出一致型变化特征 (方差贡献率29.7 %),北美洲中部、亚洲西北部、欧洲南部与南美洲北部、非洲低纬度地区、 印度反向变化特征 (方差贡献率9.8 %)。
4 主要气候因子影响区域高温频次的可能机理
4.1 气候变暖
高温频次EOF分析的第一模态表现为一致型分布, 配合时间序列可以发现北半球高温频次有整体增多的趋势,这种趋势与气候变暖的趋势相似。 很多研究表明,全球气候变暖将使极端高温事件增多[7-9]。进一步比较两者之间的关系, 计算出1979-2019年夏季北半球平均气温的逐年变化, 将之与高温频次EOF 第一模态的时间序列(PC1)对比并求其相关系数。 发现两者在过去41 a 中都呈现出在波动中上升的趋势, 尤其是1995-1999年间两者的变化幅度吻合很好, 在 1998年PC1和平均气温的值都达到1979-2006年时间段内的高点。通过计算发现两者相关系数为0.96 并通过99 %的显著性检验,这说明高温日数第一模态的时间系数与北半球平均温度有高度相关(图 3)。
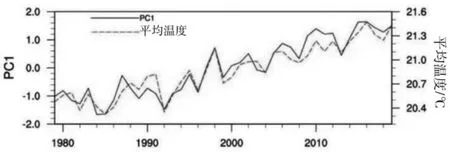
图3 北半球平均气温变化与高温日数EOF 第一模态时间系数对比(气温单位:℃)
4.2 热带扩张
在气候变暖的背景下, 大气环流也会发生相应变化,从而对高温频次产生影响。 过往研究指出副热带高压是副热带地区高温的重要成因之一, 位势高度呈现正异常利于形成下沉气流, 维持晴好的天气条件,容易形成高温天气[10-11]。 为探究气候变暖是如何通过大气环流影响高温变化的, 将高温日数变化所对应的北半球大气环流变化特征进行检查。 这里选择的环流要素为500 hPa 高度场,将环流要素作为因变量,高温日数EOF 中的时间系数作为自变量,根据相关系数和回归系数的关系式, 计算出北半球格点所对应的回归系数。 在计算之前,先求出北半球格点每年夏季(6-8月)500 hPa 位势高度的平均值。 由图4 可知, 与高温频次EOF 第一模态回归后的中纬度高度场(30°N-45°N)表现为一致的正异常,并且在500 hPa 上 130°W-150°W,40°N-45°N和 30°E-50°E,30°N-40°N 区域有正值中心, 位势高度偏高超过50 gpm。 从过去41 a 高度场平均态可以看出北半球500 hPa 副热带高压带位于 20°N-30°N 附近。 中纬度高度场偏高说明近些年来, 北半球副热带高压有向北侧边缘扩张的趋势, 回归系数表明这样的扩张与高温频次增多有显著的正相关关系。 同时,多项研究表明哈德莱环流也在近几十年中有所增强[12-13]。 这可能说明伴随全球变暖, 副热带高压向北扩张和哈德莱环流的增强,有利于北半球高温日数的增加。

图4 北半球35℃高温EOF 第一模态与500 hPa 高度场的回归系数分布,打点区域通过90 %显著性检验(黑色实线为平均位势高度线,单位:gpm)
4.3 海表温度
北半球高温的变化除与气候变暖有关之外,还会受到海洋等下垫面的影响[14-18]。 为研究北半球高温日数与海表温度之间的关系, 计算北半球同期海表温度的回归系数。 使用的资料为美国国家海洋和大气管理局的ERSSTv5 海表温度数据集。 首先计算北半球海表每个格点每年夏季(6-8月)的逐月平均值作为因变量, 以高温日数EOF 第二模态的时间系数作为自变量, 得到每个格点海表温度与高温日数的回归系数(图5)。
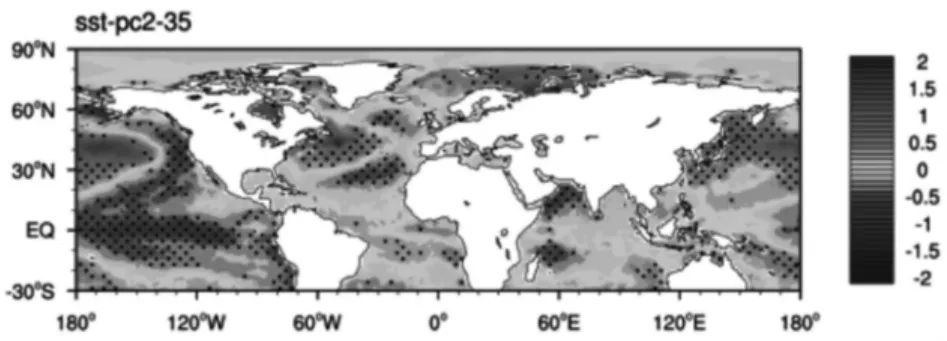
图5 北半球35 ℃高温日数EOF 第二模态与海表温度的回归系数分布,打点区域通过90 %显著性检验
在第二模态中, 高温日数和海表温度的回归系数表现出大尺度异常并有多个正异常区和负异常区。 在北大西洋,有三个异常区并通过90 %显著性检验,分别位于北大西洋高纬度(10°W-30°W,50°N-60°N)、北大西洋中纬度(35°W-70°W,30°N-50°N)、北大西洋低纬度(30°W-50°W,20°N-30°N)范围内。当时间序列增多一个单位时, 大西洋海温自北向南表现出“低-高-低”的分布异常,高值中心偏高接近1℃,低值中心偏低接近1 ℃。 这与北大西洋三极型海温异常非常相似, 有研究表明该型海温异常对于欧亚大气环流和气候有重要影响[19-20]。 根据北大西洋的异常海温分布,定义一个三极型海温指数,即

M 为(35°W-70°W,30°N-50°N)海域的海温距平值;S 为(10°W-30°W,50°N-60°N)海域的海温距平值;N 为(30°W-50°W,20°N-30°N)海域的海温距平值。 通过计算,发现在1993-1997年间NATI 指数与高温日数第二模态时间序列都表现出增加和减小逐年交替出现的变化趋势, 这五年两者相关系数为0.96, 而在 1979-2019年两者的相关系数为 0.49 并通过显著性检验。
在太平洋上, 高温日数和海表温度的回归系数表现出两个大尺度异常区。 正异常区位于 (140°W-130°E,20°N-50°N)范围内,负异常区位于(100°W-170°W,10°S-10°N)范围内。 当时间序列增多一个单位时,太平洋海温自北向南表现出“高-低”的分布异常,高值中心偏高接近1 ℃,低值中心偏低接近1 ℃。在这里重点关注赤道中东太平洋海域的显著负异常区,(120°W-170°W,5°S-5°N) 范围内海表温度和高温日数第二模态呈负相关关系并通过90%显著性检验,回归系数<-0.5。 而 NINO3.4 正是描述(120°W-170°W,5°S-5°N)范围内平均海面温度异常和 ENSO的重要指标之一。 将 1979-2019年NINO3.4 指数与第二模态时间系数做相关性分析, 发现两者相关系数为-0.29 并通过显著性检验。 同时注意到东太平洋的负异常区在空间尺度上比ENSO 更大, 这与Bin Wang 在研究中提出的Mega-ENSO 非常相似, 他在研究中指出 1958-2010年间 ENSO 指数和 Mega-ENSO 指数的相关系数为 09.1[21]。 参考 Bin Wang 的方法,将(70°W-170°W,10°S-10°N)海域的海温距平值定义为Mega-ENSO 指数,计算发现定义的Mega-ENSO 指数与 NINO3.4 指数相关系数为 0.89 并通过显著性检验。 之后,将 1979-2019年Mega-ENSO 指数与第二模态时间系数做相关分析, 发现两者相关系数为-0.27 并通过显著性检验。
通过以上分析,发现北大西洋三极型海温异常、ENSO、Mega-ENSO 可能是影响高温日数第二模态时间系数的因子之一。
5 小结
高温日数可能与气候变暖关系密切,1979-2019年500 hPa 副热带高压向北扩张,哈德莱环流有所增强,意味着热带有向北扩张的趋势,这可能会对北半球高温日数有影响。 北半球平均最高气温和非洲北部、 北美洲南部以及中东地区平均最高气温呈正相关关系,和平均最高气温的标准差呈负相关关系。 说明非洲北部、 北美洲南部以及中东地区高温日数增多的过程中, 最高气温平均值变化的贡献要大于标准差变化的贡献。 在大西洋,三个主要异常中心分别位于北大西洋高纬度、中纬度和低纬度海域,在太平洋,异常区域主要位于赤道中东太平洋,说明北大西洋三极型 SST 异常、ENSO、Mega-ENSO 可能是影响因子之一。 当 NINO3.4、Mega-ENSO 指数增高(减小)时,印度高温日数增多(减少),非洲西北部高温日数减少(增多)。 NATI 指数增高(减小)时,非洲西北部、北美中部偏南地区高温日数增多(减少),印度高温日数减少(增多)。

