基于电磁感应透明效应的超慢矢量光孤子

陈志明，谢红强，王 岳，谭嘉进

(东华理工大学 理学院，江西 南昌 330013)

矢量光孤子是非线性光学中重要的光孤子类型，这是由光的矢量性导致的结果。不同偏振方向分量的非线性光波会发生相互作用，当自相位调制(self-phase modulation，SPM)和交叉相位调制(cross-phase modulation，XPM)产生的非线性效应与衍射或色散效应平衡时，即形成空间或时间矢量光孤子(Manakov, 1974)。由于矢量光孤子具有丰富的非线性物理特性与潜在的应用价值(Malomed et al., 2019)，人们在许多不同的非线性光学体系中研究了矢量光孤子(Skryabin et al., 2004; Rand et al., 2007;Assanto et al., 2008; Li et al., 2018;Guo et al., 2019;Ma et al., 2019)。

矢量光孤子的早期研究主要集中在光与非共振被动介质的相互作用。利用被动介质产生的克尔非线性效应十分微弱，故需提供强激光场来获得较强的非线性效应。另外，为了避免介质对光场的吸收，光场的频率必须远离介质的共振频率，使得矢量光孤子的传播速度接近于光速，从而导致人们不便主动操控光孤子。幸运的是，电磁感应透明(electromagnetically induced transparency,EIT)效应的出现顺利地克服了被动介质中所遇到的困难(Fleischhauer et al., 2005)。EIT 技术显现了许多重要的物理性质：①有限地抑制了介质对光场的吸收；②显著地减小光场的传播速度；③极大地增强了非线性光学效应等。基于此，人们在共振介质系统中研究了时间矢量孤子(Hang et al., 2008; Si et al., 2009)、空间矢量孤子(Qi et al., 2011; Deng et al., 2019)以及Thirring型光孤子(Li et al., 2017; Qi et al., 2018；Chen et al., 2019)等。目前尚未利用Λ-梯型五能级相干原子系统研究时间矢量光孤子。该体系具有以下优点：①只需单组份原子就可实现矢量孤子模型；②探测光场的两个偏振分量的群速度易实现相互匹配，有利于增强克尔非线性效应。

本次利用Λ-梯型五能级相干原子系统，研究基于双EIT的超慢矢量光孤子。首先，根据多重尺度展开法，求解描述系统原子布居的几率幅方程和光场传播的麦克斯韦方程，导出了探测光场两个偏振分量所满足的耦合非线性薛定谔方程。其次，通过选取适当的物理参量，增强系统产生的自克尔和交叉克尔非线性效应，从而可与群速度色散效应相平衡。在此条件下，探测光场的左旋和右旋偏振分量可形成稳定的弱光时间矢量孤子。该矢量光孤子传播的速度可降至10-5c，且所需输入的光功率低至微瓦量级。最后，将证明该系统可形成Manakov时间矢量光孤子。该研究结果不仅对弱光非线性光学领域的发展有较重要的理论价值，而且在光信息处于与传输、弱光全光开关设计等方面具有一定的理论指导意义。

1 理论模型

考虑一个Λ-梯型五能级冷原子系统分别与一束较弱的脉冲型探测光场(中心频率ωp/2π)和两束较强的连续型控制光(中心频率分别为ωc1/2π和ωc2/2π)相互作用(图1)。线性偏振的探测光场Ep可分解为右旋偏振光(σ+)和左旋偏振光(σ-)，并分别与能级跃迁|1〉↔|3〉和|1〉↔|4〉耦合。控制光场Ec1和Ec2分别耦合能级跃迁|2〉↔|3〉和|4〉↔|5〉。因此，Λ-梯型系统可看成为|1〉↔|3〉↔|2〉的Λ型系统和|1〉↔|4〉↔|5〉的梯型系统组成，则该系统会形成双EIT。

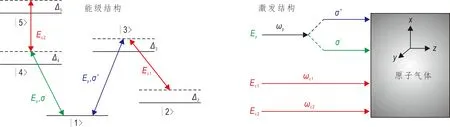
图1 原子系统的能级结构与激发构型图Fig.1 Energy level structure and excited configuration of atomic system

假设探测光场和控制光场均沿着z轴传播，则它们的电场强度矢量可表示为E=∑l=p,c1,c2elElei(k1z-ω1t)+c.c.，其中el(El，kl)表示光场偏振方向的单位矢量(包络函数，波矢)。在薛定谔表象下，描述系统原子布居的几率幅和探测光相互作用的运动方程为：

(1a)

(1b)

(1c)

(1d)

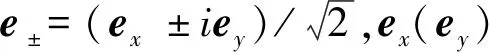
在慢变包络近似下，描述探测光场传播的运动方程为：

(2a)

(2b)

其中定义κ13=Nω|p13·e+|2/(2ћε0c)和κ14=Nω|p14·e-|2/(2ћε0c)为探测光场的传播系数。

上述的物理模型可以在实际的原子系统中实现。选取五能级Λ-梯型87Rb原子系统，其能级分别为|1〉=|52S1/2,F=1,mF=0〉,|2〉=|52S1/2,F=2,mF=1〉,|3〉=|52P1/2,F=1,mF=1〉,|4〉=|52P1/2,F=2,mF=-1〉和|5〉=|52D1/2,F=3,mF=-1〉。因此，各个能级的衰减率为γ1=γ2=1 kHz，γ3=γ4=6 MHz和γ5=0.4 MHz。假设87Rb原子密度为N=3.67×1011cm-3，则κ13=κ14=1.0×1010cm-1·s-1。

2 非线性包络方程和巨克尔非线性效应

2.1 非线性包络方程的推导

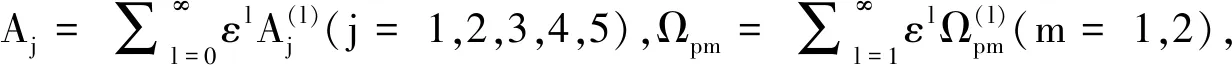
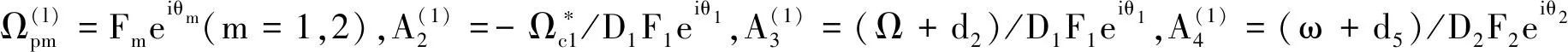
图2表示探测光场的线性色散关系的虚部Im(K1)和实部Re(K1)与频率偏移量ω的函数关系(以右旋偏振分量为例)。虚部和实部分别表示原子介质对探测光场的吸收和原子介质体系的色散。虚线表示无控制光场输入系统，则探测光场的吸收曲线在中心频率附近出现很强的吸收。实线表示有控制光场输入系统(即Ωc1≠0)，则吸收曲线在其中心频率附近产生了一个透明窗口，可有效抑制介质对光场的吸收，即EIT效应。同时，线性色散关系的实部在共振频率点附近也出现明显的改变，由此可实现超慢群速度。

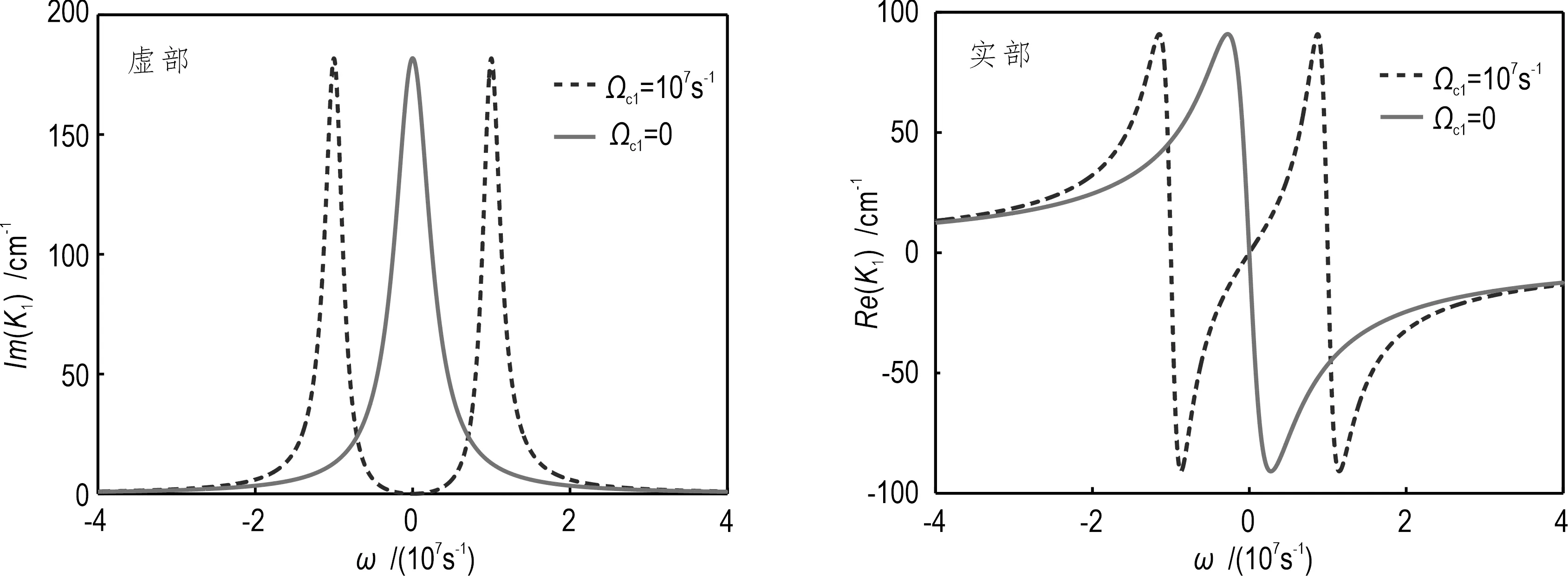
图2 探测光场线性色散关系Fig.2 Linear dispersion relation of the probe field

在二阶(l=2)近似下，导出可解条件i[∂Fm/∂z1+(∂Km/∂ω)∂Fm/∂t1]=0，其中vgm=(∂Km/∂ω)-1表示包络函数在原子介质中传播的群速度。其他的二阶解为：

(3a)

(3b)

在三阶(l=3)近似下，非线性效应将扮演着重要的角色。结合一阶和二阶近似解，导出探测光场两个偏振分量的耦合非线性薛定谔方程(m=1,2)：

(4)

其中定义τ=t-z/vg，vg=2vg1vg2/(vg1+vg2),Um=εFme-αmz,αm=Im[Km(ω=0)]，δ=(1/vg1-1/vg2)和Km2=∂2Km/∂ω2。式中的系数Wml(m=l)和Wml(m≠l)分别表示SPM和XPM产生的非线性效应，其表达式为：

(5a)

(5b)

通过引入部分关系式，可将方程(4)转化为无量纲形式(m=1,2)：

(6)

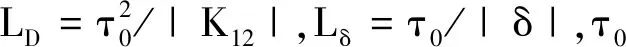
2.2 系统产生的巨克尔非线性效应

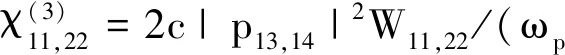
3 时间矢量光孤子

当系统的自相位调制和交叉相位调制系数满足关系g11g22=g12g21时，则该系统可支持稳定传播的亮-亮、亮-暗、暗-暗等形式的时间矢量光孤子。本次研究的物理模型是一个有寿命展宽的原子系统，方程(6)中的系数均为复数。当该系统满足EIT条件时，方程(6)中各个系数的实部将远远大于其虚部，故各系数的虚部可以忽略不计。

为了研究的简便，在此只给出亮-亮矢量光孤子解。该解的具体形式为：

u1=V1sech(Aσ+Bs)exp[i(P1σ+Q1s)]

(7a)

u2=V2sech(Aσ+Bs)exp[i(P2σ+Q2s)]

(7b)

式中，P1=(B+gδA)/(g1A),P2=(B-gδA)/

结合上述的物理参数，以及U0=39.2 MHz,τ0=5×10-8s，则二阶色散为K12=K22=-(1.99-0.20i)×10-14s2·cm-1。同时，系统的特征色散长度等于特征非线性长度，即LD=LNon=0.13 cm，特征群速度失配长度为Lδ=141.3 cm。故方程(6)中的各个无量纲系数分别为g1=g2=-1,g11=g12=1.0-0.009i,g21=g22=1.0-0.019i,gδ=LD/Lδ=0.001，则各系数的虚部和群速度失配系数可以忽略，且满足g11g22=g12g21。

图3表示亮-亮时间矢量光孤子在原子介质中的稳定传播图。在进行数值模拟时，图3a和3b的自由参量选为P1,2=1,Q1,2=0,V1=0.8。图3c和3d的自由参量选为P1,2=2,Q1,2=1,V1=1。从图3可知，探测光场的左旋和右旋偏振分量可以在原子介质中稳定地传播，是群速度色散和非线性效应相互平衡的结果。

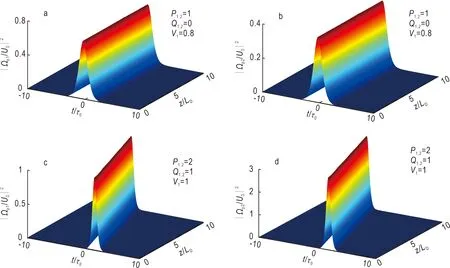
图3 时间矢量光孤子的稳定传播Fig.3 Stable propagation of temporal vector optical solitons

根据上述的数值结果发现，该系统可实现Manakov可积模型，并形成稳定的Manakov矢量光孤子。将相应的数据代入方程(6)，则该方程可简化为：

(8a)

(8b)

则亮-亮Manakov矢量孤子解为u1=cos(θ)sech(σ)exp(is/2)和u2=sin(θ)sech(σ)exp(is/2)，其中θ为自由参量。图4表示Manakov时间矢量光孤子的稳定传播。在数值模拟时，选定自由参量θ=π/4。

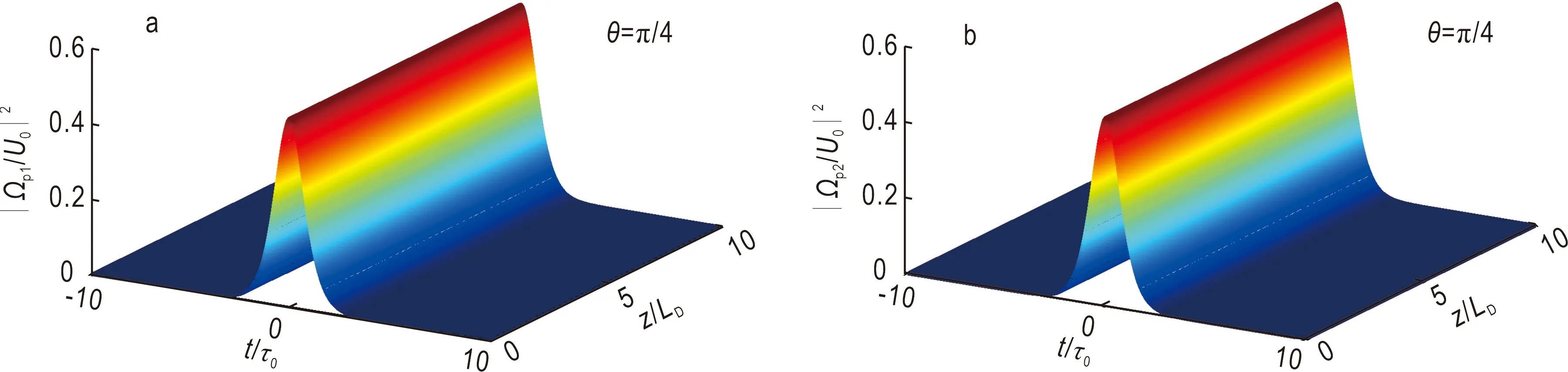
图4 Manakov时间矢量光孤子的传播图Fig.4 Propagation of Manakov temporal vector optical soliton

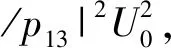
4 结论

本次研究了基于电磁感应透明效应的Λ-梯型五能级原子中的超慢矢量光孤子。利用多重尺度展开法，推导了探测光场两个偏振分量的耦合非线性薛定谔方程。可知，当系统产生的克尔非线性效应与群速度色散效应相互平衡时，探测光场的两个偏振分量可形成稳定的弱光时间矢量孤子。结果显示，该矢量光孤子传播的速度可降至10-5c，且所需输入的光功率低至微瓦量级。同时证明了该系统可形成Manakov时间矢量光孤子。该研究结果不仅对弱光非线性光学领域的发展有较重要的理论价值，而且在光信息处理与传输、弱光全光开关设计等方面具有一定的理论指导意义。