低压驱动V形直线超声电机的设计
黄卫清,杨成龙,沈兆琛,薛昊东,安大伟
(广州大学机械与电气工程学院,广东广州510006)
1 引 言
压电直线电机具有定位和速度控制精度高、结构设计灵活,易实现装置的小型化和轻量化等特点,广泛应用于精密驱动等相关领域[1-3]。1982年,Sashida[1]率先提出基于兰杰文振子的直梁式直线超声电机,通过梁两端的兰杰文振子在直梁上产生行波,推动动子。1998年,Kurosawa[4]首次提出一种V形直线超声电机,利用双兰杰文振子连接形成的V形结构作为定子,通过同时激发定子的对称与反对称模态,在定子驱动足形成处椭圆运动轨迹,由定、动子之间的摩擦作用由驱动足推动动子,该电机最大空载速度达到3.5 m/s,最大输出力达到51 N(驱动电压的有效值为500 V)。2006年,Ibrahim[5]设计了一种基于杆结构的V形定子,将杆弯折成V形,在杆端部布置兰杰文振子,于V形杆尖端的驱动足获得了较大振幅。在国内,杨东[6]等人于2009年将矩形变幅杆应用于Kurosawa电机定子的振子上,相对于原来的突变截面杆,连续变截面杆具有更高的振动能量传输效率,该电机的最大推力为21.4 N,最大速度为235 mm/s(驱动电压为300 Vpp)。2017年,李晓牛[7]等人设计了一种贴片式V形压电直线电机,采用椭圆柔性铰链将两个双面贴着压电片的梁连接在一起形成V形结构,并利用定子纵振和弯振的耦合模态工作,其最大空载速度达到1.2 m/s(驱动电压为350 Vpp)。2019年,姚志远[8]等人提出了一种板形压电直线电机,定子由两厚度为8 mm的矩形板联结成V形结构,特别适用于狭窄空间的作业。上述研究工作中,V形超声电机已经衍生出多种不同的结构,获得了优良的机械性能。
压电致动器已广泛应用于航空航天、镜头调焦系统、激光系统、微型机器人关节及微位移驱动平台等领域。V形直线压电电机经过20余年的发展,其结构形式呈现多样化,输出性能也逐步提高。然而,基于传统兰杰文换能器结构的V形直线电机的驱动电压较高、驱动电路设计复杂,这对提高V形直线压电电机的输出效率以及推重比形成了制约,一定程度上限制了V形直线压电电机的小型化和应用范围。本文通过分析叠层压电陶瓷的低压驱动机理,设计了多层压电叠堆驱动的V形超声电机,通过设计振子结构和夹持装置结构,制作了实验样机并测试了压电振子阻抗,进一步研究了样机的驱动电压、预压力与输出特性的关系。通过采用叠层压电陶瓷振子设计,实现了V形直线电机在低压驱动下的大推力输出,可为直线压电电机设计提供参考。
2 V形直线超声电机运行机理
V形直线超声电机在运行时需要利用定子的对称模态和反对称模态,在定子驱动足产生椭圆轨迹,通过摩擦作用完成定、动子之间的运动传递。当左右两振子做同向伸缩运动时,即形成对称模态,此时,定子驱动足端面上形成竖直方向上的振动;当两振子做互为反向的伸缩运动时,即形成反对称模态,此时,定子驱动足端面上合成水平方向上的直线运动[9]。当这两种模态在驱动足的响应具有90°的相位差时,就可以在驱动足端面形成椭圆运动轨迹,通过摩擦力驱动动子。

图1 V形直线超声电机作动原理Fig.1 Working principles of V-shaped linear ultrasonic motor
其作动原理如图1所示,图中a,b,c和d对应定子一个工作周期中的不同运行状态。当定子运动状态处于反对称模态的最大伸长位置(a)时,定子驱动足端面与动子(滑轨)脱离接触;在定子运动状态从a到b(对称模态的最大收缩位置)的过程中,定子驱动足与动子持续脱离,对动子不产生驱动作用;在定子运动状态由b变化至c(反对称模态反方向的最大伸长位置)的过程中,在最后一刻,驱动足与动子开始接触;在定子运动状态由c至d(对称模态的最大伸长位置)的过程中,驱动足与动子持续接触,在预压力和摩擦作用力下,驱动足带动动子向右移动了一段距离;在定子运动状态由d到a的过程中,驱动足与动子持续接触,又将滑轨向右带动了一段距离,直至最后一刻脱离接触,驱动足完成了空间上的一个椭圆运动,而动子完成一个直线步进运动。通过互换两振子激励信号的相位,就可以实现电机的正反转,促成动子的反向运动。
根据电机的作动原理和施加在振子上的周期信号,可以将定子简化后推导出电机驱动足的轨迹方程。将定子假设为简单的V形梁,对左右两振子施加正弦激励信号[10],设在梁1(振子1)上施加激励信号后对应的振动位移响应函数为:
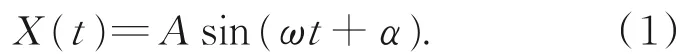
设在梁2(振子2)上施加激励信号后对应的振动位移响应函数为:
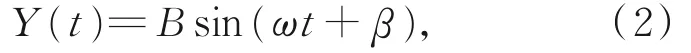
其中:A,B为对应压电陶瓷的位移响应幅值,α,β为对应激励响应的相位角。将式(1)和式(2)中的参数t消去并结合公式:
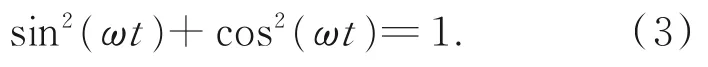
可得:

当激励信号相位差为90°时,也就是β−α=π/2时,式(4)为:

式(5)是一个椭圆方程[11]。这表明,当对定子上的左右两组压电陶瓷施加相位差为90°的激励信号时,这两组压电陶瓷的位移响应在空间上形成90°相位差,就可以在定子驱动足处形成椭圆运动轨迹[12]。
3 低压驱动电机结构设计
图2 为设计的V形直线超声电机结构,电机由基座、预紧装置、夹持装置、滑轨、陶瓷条和振子等构成。动子采用带导向滑块的VRU6-210滑轨,可以通过螺栓连接固定在实验平台上。加装基座增加定子高度,使驱动足端面和动子的滑轨平面保持全面接触。此外,基座尾部加工有螺纹孔,将螺栓套入弹簧与基座串联,配合夹持装置给定子与滑轨施加初始的预压力。
3.1 低压驱动原理

图2 V形直线超声电机整体结构示意图Fig.2 Structure diagram of V-shaped linear ultrasonic motor
叠层压电陶瓷通常选用相同厚度的压电陶瓷片叠加,由电极片将极化方向相反的压电陶瓷片隔离。样机单振子采用8片型号为PZT-8的压电陶瓷片组成的叠层陶瓷组,陶瓷片之间使用铜极片分离,相邻压电陶瓷片的极化方向相反。压电陶瓷片的尺寸规格为20 mm×20 mm×0.5 mm,中间有一个φ4 mm的圆孔,通过螺栓连接夹紧,结构如图3所示。压电陶瓷片极化方向与螺栓孔轴线方向一致,以便使振子在中心轴方向产生最大位移。加工时陶瓷片两侧镀银层,可以使电荷在陶瓷片两侧均匀分布,减小对输出性能的影响。

图3 叠层压电陶瓷的结构模型Fig.3 Structural model of laminated piezoelectric ceramics
叠层中的压电陶瓷采用机械结构上的串联、电学结构上的并联的形式[13]。从机械结构上看,其串联形式类似于弹簧,每片压电陶瓷在极化方向上的位移起到了一个累加的效果,从而获得了较大的输出位移;从电学结构上看,叠层压电陶瓷是由几何、物理参数相同的压电片组成,各片之间有电极以便给压电片施加驱动电压,由于采用的是电学上并联的连接方式,施加至各压电片中的驱动电压都是U。
压电陶瓷片两表面上所施加电压U和电场强度E的关系可表示为[14]:

其中t为单层压电陶瓷片的厚度。
单片压电陶瓷在极化方向上的输出位移Δl1可表示为:

式中d33为压电应变系数。
由N片压电陶瓷组成的叠层压电陶瓷在厚度方向的输出位移ΔlN为:

根据式(7)和式(8)可以看出,当单片压电陶瓷的厚度和叠层压电陶瓷的总厚度相同,且两者的输出位移一样时,单片压电陶瓷所需的驱动电压是叠层压电陶瓷的N倍,所以使用叠层压电陶瓷的定子可以实现电机的低压驱动。
3.2 V形振子结构设计
V形定子结构如图4所示,所选材料为45#钢。前端盖采用两方柱体相交的结构,端面到驱动足逐渐收缩形成侧棱。后端盖设计成长方体,作为两个单独元件。前端盖打有螺纹孔,后端盖为通孔,利用高强度六角螺栓将前端盖和后端盖之间的压电陶瓷和铜极片压紧。整个电机采用了两组共计16片压电陶瓷,每片压电陶瓷接触两片铜极片,位于同一振子上的铜极片用导线相连,构成A,B两相。
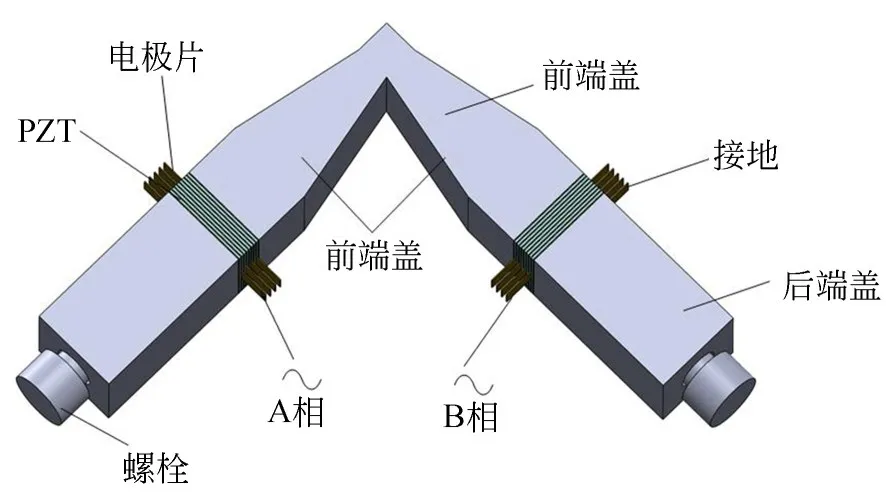
图4 V形压电直线电机定子结构Fig.4 Stator structure of V-shaped piezoelectric linear motor
3.3 基于柔性铰链的驱动足设计
柔性铰链具有无间隙、无摩擦和运动灵敏度高的优点[15-16],在压电电机中得到了广泛关注和应用。为了方便电机加工,同时节约成本,增加经济效益,采用类V型柔性铰链,其结构如图5(a)所示。两兰杰文振子的柔性铰链相连接,在连接处形成驱动足,两柔性铰链的端部聚合形成侧楞,与定子形成线接触,如图5(b)所示。一般情况下,使用较为复杂的摩擦模型可以有效提高精确度,接触面积越大,机械性能越好。但在定子驱动动子的过程中,摩擦会产生热量,动子多次的往返运动会造成摩擦损耗,不利于电机长时间的稳定输出,故采取线接触的方式驱动动子。

图5 V型柔性铰链和驱动足结构Fig.5 Structure of V-shaped flexible hinge and driving foot
3.4 夹持装置设计
夹持装置对定子施加垂直于动子运动方向的预压力,使定子和动子之间保持一定程度的接触,提供平行于动子运动方向的摩擦力[17-18]。定、动子之间通过摩擦作用将定子的振动转换成动子的直线运动[19]。
本文设计了两种夹持方式,第一种采用一端固定铰支,另一端提供预压力的铰支梁结构,如图6 所示。这种铰支梁结构是绕固定铰链端旋转的,而不是定子质心,当电机切换驱动电压使它正反转时,一端固定铰支的铰支梁结构会导致定动子之间接触力不同,电机正反输出性能不对称;此外,振子弯振模态的转角处最大处受到限制,从而抑制了弯振模态的激发,影响了电机工作的稳定性和输出性能。

图6 单边铰支电机夹持装置Fig.6 Single-side hinged motor clamping device
第二种为自适应夹持结构,如图7所示。在垂直于单个振子轴线的方向,用两个对称的两端固支的弹性梁顶住加装凹槽的螺栓,并在前端盖变截面处黏贴弹性垫片,用两块亚克力板将电机夹在中间,用螺钉与螺母固定上下板。相较于第一种,自适应夹持装置是轴对称的,会降低电机正反转的差异;当给定子施加预压力时,左右两振子底部的弹性梁会使定动子之间保持一定的预压力,而振子弯振模态的转角最大处则不像第一种夹持装置一样与固定铰支端和预压力端相连接,只是采用支撑杆限制定子的位置,降低了对振子弯纵振的影响,从而保证电机能够稳定工作,提升了输出效率,故夹持装置最终选择自适应夹持装置设计方案。

图7 自适应电机夹持装置Fig.7 Adaptive motor clamping device
4 样机实验及分析
图8 所示为电机性能测试平台的实物图。实验装置主要包括气浮稳定实验平台、信号发生器、功率放大器、示波器、V形直线超声电机样机、位移传感器、压力传感器和负载砝码等。

图8 电机性能测试装置实物图Fig.8 Physical image of motor performance test device
4.1 V形振子模态与阻抗测试实验
4.1.1 模态测振实验
用三维多普勒激光测振仪(PSV-300F)对V形定子进行模态测试实验,其对称模态和反对称模态振型如图9所示。根据对称模态和反对称模态的特征频率初步确认电机的驱动频率区间大致在32~41 kHz。将测试结果与有限元仿真结果进行比较,其结果见表1。模态特征频率值与仿真值存在一定误差,这主要是由于仿真过程中的约束边界条件及材料选择均采用理想化模型,而制造过程中引进了加工装配误差和固有材料缺陷,以及实际的物理场边界约束差异。
4.1.2 阻抗测试实验
为保证电机工作状态稳定,动子正反转的输出性能相同,需验证V形定子左右两振子振动特性的一致性。采用阻抗分析仪对两边振子进行阻抗测试,振子1(W1)和振子2(W2)的阻抗特性曲线如图10所示。在特征频率点附近,阻抗曲线会出现一个波谷和一个波峰,波谷处即为特征频率点,两振子在驱动频率区间(32~41 kHz)出现了两个特征频率点,依次为反对称模态和对称模态,两振子的阻抗曲线和相位曲线在整个测试频率范围大致相同,振动特性较为一致。
4.2 激励频率与空载速度关系分析

图9 定子振型Fig.9 Mode shapes of stators
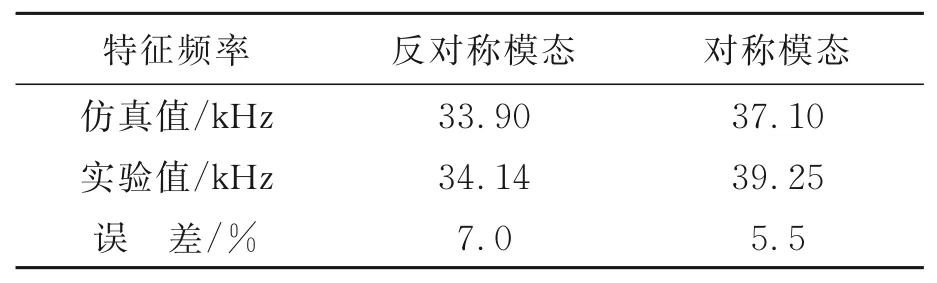
表1 两模态特征频率的仿真值与实验值Tab.1 Simulation and experiment values of natural fre⁃quency of two models
基于振子模态测试与阻抗测试结果,V形直线超声电机的对称频率与反对称频率相差约5 kHz,利用解析方法得到电机最佳驱动频率存在一定困难,本文采用实验方法测试电机激励频率与空载速度的关系,以获取电机的最佳驱动频率。
在空载条件下,给电机施加50 N的预压力,分别给两振子施加50 Vpp、两相相位差为90°的正弦驱动电压,用秒表测量电机滑轨输出满行程所用的时间,在同等条件下记录5次并取平均值,得到电机在此频率下的输出速度。测量频率为34.5~39 kHz激励信号下电机的速度,最终得到电机输出速度随频率的变化曲线,结果如图11所示。

图10 单相振子阻抗实验结果Fig.10 Results of single phase oscillator impedance
由图11可以看出,当激励频率在对称模态特征频率和反对称模态特征频率附近时,电机的空载转速处于较低水平,而最佳工作频率处于对称模态频率和反对称模态频率之间,在激励频率为37 kHz时电机的输出速度达到最大,为1.221 m/s,即电机的最佳驱动频率处于37 kHz附近。最佳驱动频率并不是在反对称模态特征频率(34.14 kHz)或是对称模态特征频率(39.25 kHz)附近,这是因为电机的运行需要振子驱动足在水平方向和竖直方向均满足一定的振动幅度,以耦合形成驱动足质点的椭圆运动轨迹。

图11 速度与激励频率的关系Fig.11 Relationship between velocity and excitation fre⁃quency
当电机驱动频率在反对称模态特征频率附近时,驱动足沿水平方向的振幅最大,但此驱动频率离对称模态特征频率较远,驱动足竖直方向的振幅较小,所以此驱动频率下的电机输出速度不是整个驱动频率范围内最大的;同理,当电机驱动频率在对称模态特征频率时,输出速度也不是最大的。此外,当驱动频率低于36 kHz或者高于38 kHz时,动子导轨的运动较慢或者无法被驱动。因此,后续实验选定的驱动频率为36~38 kHz。
4.3 预压力对输出速度的影响
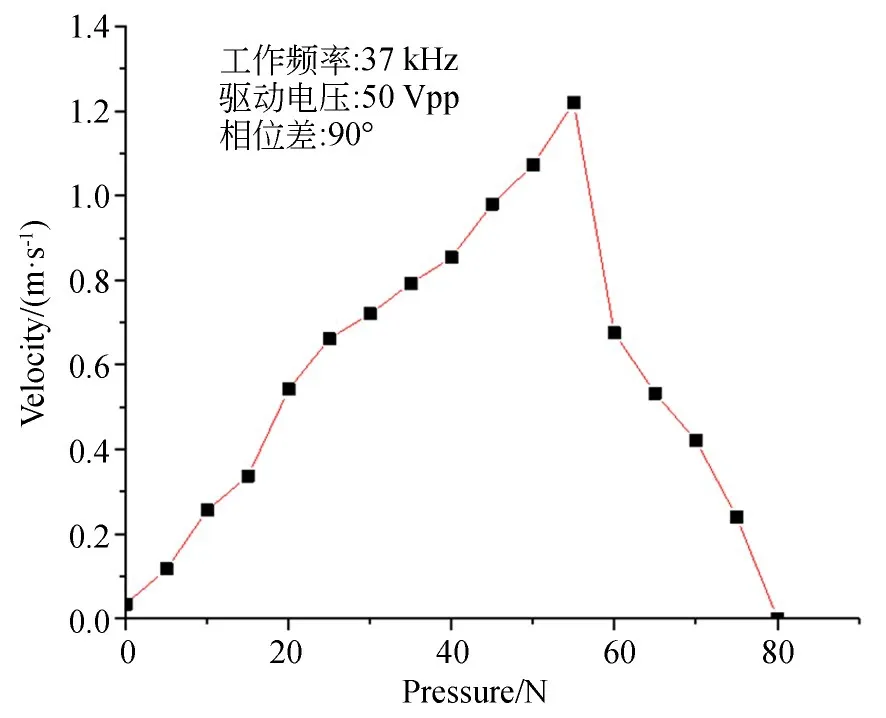
图12 不同预压力下的电机速度曲线Fig.12 Speed curves of motor under different pre-pres⁃sures
电机定子与动子之间需要靠摩擦力实现运动传递,而预压力与摩擦力呈正相关关系,所以预压力的设置对电机输出性能有很大的影响。空载条件下,分别给两振子施加50 Vpp,37 kHz、两相相位差为90°的正弦驱动电压,通过转动在串联基座和压力传感器的螺栓来调节预压力,测量在预压力为0~80 N内电机的输出速度,得到预压力与输出速度的关系,其结果如图12所示。结果表明,动子输出速度随着预压力的增大先增大而后减小,在预压力为50 N附近,动子有最大空载速度且运行稳定;当预压力继续增大并接近60 N时,空载速度开始陡降。这是由于当预压力较小时,无法为摩擦力提供足够大的法向压力,驱动足和滑轨之间会出现打滑现象;而当预压力较大时,驱动足端面的椭圆运动受到阻碍,继续增加预压力则会直接将动子锁死。
4.4 电机空载输出和负载性能实验
空载条件下,给电机施加50 N的预压力,分别给两振子施加37 kHz、两相相位差为90°的正弦驱动电压,测得的电机在不同激励电压下的速度曲线,结果如图13所示。由图可知,随着激励电压的增加,驱动足振幅逐渐增大,动子的空载速度随之加快。

图13 不同激励电压下的电机速度曲线Fig.13 Speed curves of motor under different excitation voltages
电机的负载特性是衡量电机性能的重要指标,分别给两振子施加50 Vpp,37 kHz,两相相位差为90°的正弦驱动电压,给滑轨一端系上砝码,更换不同砝码以测得电机在不同负载下的输出速度,得到负载和输出速度的关系如图14所示。从图中可以看出,随着砝码质量的增加,电机的输出速度下降,电机的最大输出力为25.8 N。此外,当负载不超过24 N时,电机运行比较平稳。
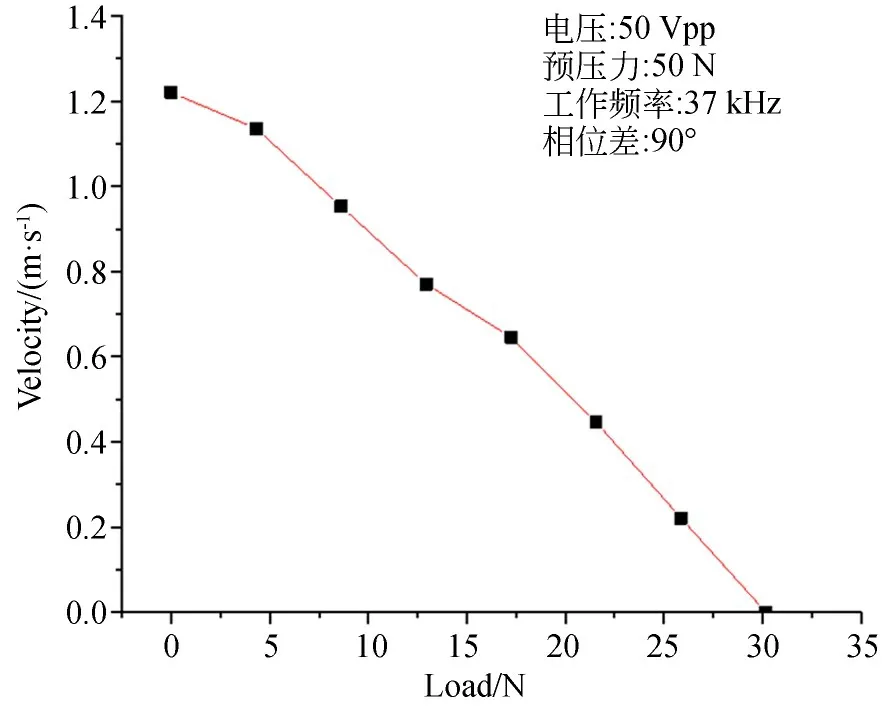
图14 电机的负载-速度曲线Fig.14 Load-speed curve of motor
5 结 论
本文提出了一种低压驱动的V形直线压电电机,对该电机的运行机理进行了理论分析,阐明了叠层压电陶瓷的低压驱动原理,开展了V形直线压电电机及其夹持机构的结构设计,采用阻抗测试实验和多普勒激光测振实验研究了低压驱动电机的特征模态与特征频率,进一步开展了样机实验,研究了电机输出速度与激励信号频率、预压力、电压和负载的关系。实验结果表明,在低压50 Vpp、预压力50 N的条件下,样机的最大空载速度为1.221 m/s,最大负载为25.8 N,输出性能良好。

