基于光程变化量的反射式光学系统敏感度理论分析与降敏设计方法

孟庆宇，汪洪源，王 维，秦子长，3，王晓东

（1.哈尔滨工业大学空间光学工程研究中心，黑龙江哈尔滨150001；2.中国科学院长春光学精密机械与物理研究所，吉林长春130031；3.中国科学院大学，北京100049）

1 引 言

反射式光学系统已有400余年的发展历史［1］，并广泛地应用于大型光学系统中。从20世纪至今，随着宇宙科学、地球观测等领域对高分辨率成像的需求，大口径、长焦距反射式光学系统的体积越来越大，光学系统的焦距已增长到数十米至数百米的尺度，口径尺寸达到了数米至数十米的量级。反射式光学系统虽然构型相对简单，光学元件数量少，但随着焦距与口径的增大，光学系统的加工难度与装调敏感剧增，这为大型光学仪器的实现带来了挑战，消耗了巨大的经济与时间成本［2-3］。

光学系统的最终性能不仅取决于光学设计结果的好坏，还取决于建造过程中对于面形加工、装调位置、系统稳定性等各项误差因素的控制，而从过往经验来看，这些实际误差因素在光学系统设计中占据主导地位［4-5］。针对这一问题，在大口径、长焦距反射式系统的研制当中，一方面要通过CAA、主动光学、精密温控、高刚度高稳定性光机结构等手段实现更高精度的误差控制［6-12］；另一方面，也必须对光学系统的误差敏感性进行研究，探究光学系统误差敏感性的因素及影响规律，寻找光学系统的降敏设计方法，降低光学系统成像质量对误差控制精度的依赖，这对于降低大口径长焦距光学系统的建造难度、时间成本和经济成本具有重要的意义。

目前，针对光学系统的降敏设计方法主要有6种［13］：第一种是全局搜索优化法［14］；第二种是全差分波前误差集成优化法，该方法依靠设计软件的宏命令，在优化过程中程序不断返回可以反应光学系统敏感度的波前差分值，进而获得敏感度较优方案；第三种是光线折射角、入射角优化法［15-16］；第四种是降低光学表面倾斜对轴向彗差影响的方法；第五种是多重结构降敏设计方法；第六种是降低偏心引起的差分波前误差方法［17］。

这些降敏设计方法的理论评价主要以波像差为主，但很多情况下，光学系统初始结构的波像差较大，此时以波像差作为敏感度评价标准，往往不能直观地反映出系统的真实情况。而初始结构的选取对于误差敏感性具有非常重要甚至是决定性的影响，因此还需要发展一种更加简洁直观的评价方式，用于实现低敏感度初始设计。

影响光学系统成像质量的误差因素一般包括两大类，一是光学元件空间位置的失调，主要由光学系统装调残差、光机系统稳定性误差和温度控制误差等因素引起；二是光学元件面形误差，主要由光学加工制造以及环境因素引起。具有低敏感度特征的光学系统，应能够更好地抵抗这两种误差因素引起的成像质量下降。因此，为了能够获得低敏感度光学系统，应首先分析上述因素引起的系统光程变化，进而明确各项系统参数对于各项误差因素的敏感度模型。这是后续实现降敏设计的理论基础。

同轴两反式光学系统是大口径光学望远镜最基本、最经典的系统形式。本文以同轴两反式系统作为研究对象，采用以失调扰动引起的光程变化量（Optical Path Variation，OPV）作为评价误差敏感程度的评价标准，推导了各项失调因素引起的成像光路OPV的理论表达式，进而提出了以OPV为理论基础的降敏设计方法。

2 理论分析

2.1 光学系统敏感度理论分析方法

光学元件的位置失调主要包括偏心平移、倾斜、轴向间距与旋转，如图1所示。偏心平移失调定义为光学元件以其曲面顶点为中心，向子午方向、弧矢方向或某一合成方向平移了δ；倾斜定义为光学元件以其曲面顶点为中心，绕着子午轴或弧矢轴旋转了η；轴向间距失调定义为反射镜沿着光轴方向的位置移动了d；旋转失调是一种特殊的倾斜，特指光学元件以其曲面顶点为中心，绕着光轴进行旋转，对于同轴光学系统，当光学元件为旋转对称面形时则不存在旋转失调。光学元件的位置失调往往是综合产生的，即偏心平移、倾斜、轴向间距失调与旋转是相互伴随，相互混合的。在光学元件位置失调对成像光路光程变化的敏感度影响分析中，为了便于归纳总结，以单一类型的位置失调为研究对象。

图1 典型光学元件位置失调类型Fig.1 Typical types of optical component misalignment

图2 失调前后像面附近的成像光线Fig.2 Layout of optical system with mislignments

根据费马原理，在理想光学系统中，不同孔径、不同视场的光线经过光学系统后，应该具有相同的光程（Optical Path，OP）［18］。光学系统元件失调后，系统稳态受到破坏，成像光线光程产生变化，如图2所示，光学系统中的每根成像光线会产生因失调而引起的OPV。从几何光学角度分析，失调后每根成像光线的OPV绝对量越小，光学系统越接近失调前的状态，相应地成像质量退化也更小，这种变化量数值越小，失调对系统像质的影响也就越小。所以，失调后产生OPV数值小的系统，是低敏感度光学系统应有的特征。

如果将失调定义为｛α|α1，α2，…αn｝，其中αn代表的是一系列失调类型，那么光学系统因为失调而引起的OPV一定是失调类型与失调量的函数，即：

根据工程应用经验，因失调引起的OPV与光学系统的内部参数具有一定的相关性，则因失调而引起的OPV应该与光学系统的内部参数｛β|β1，β2，…βn｝构成一定的函数关系，即：

那么，在同轴反射式系统敏感度影响因素的理论分析中，由光学元件失调引起的OPV为光学系统敏感度的评价标准，探寻失调类型、内部参数等对光程变化敏感度的内在规律，理论揭示影响同轴反射式光学系统敏感度的重要因素，具有重要的意义。

同轴两镜光学系统是大型反射式光学系统最基本的形式，本文以两镜反射式光学系统作为基本分析对象，所采用的数学分析方法对反射式光学系统是通用的。

2.2 主镜偏心平移失调

如图3所示，同轴两镜反射式光学系统结构由主镜（Primary mirror，PM）与次镜（Secondary mirror，SM）组成，其中主镜作为光学系统的孔径光阑，光学系统位于右手坐标系中，主镜的顶点位于坐标系原点（0，0，0），z轴是系统光轴，光线沿着光轴方向传播。光线由物方无穷远发出，入射到主镜镜面M1（x1，y1，z1）点，经主镜反射后，光线入射到次镜镜面M2（x2，y2，z2）点，再经次镜反射后，光线成像于像面M3（x3，y3，z3）点。主镜与次镜可以为任意曲面面型，通常可定义为：

图3 两镜反射式光学系统结构模型Fig.3 Configuration model of two-mirror optical system

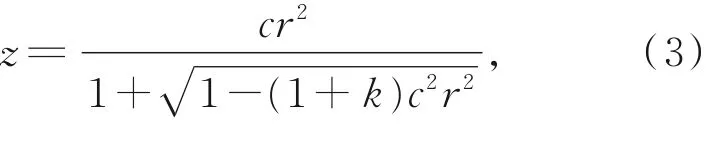
式中：z为平行于光轴的曲面矢高；c为曲面的顶点曲率；k为Schwarzschild常数，即二次曲面常数；r为曲面投影在x轴与y轴确定的平面上的点相对于光轴的径向距离，如式（4）所示：

如前所述，光线经光学系统的光程可分为3个部分，即无穷远物点至M1（x1，y1，z1）点，定义该部分光程长度为z1；M1（x1，y1，z1）点至M2（x2，y2，z2）点，定义该部分光程长度为s1；M2（x2，y2，z2）点至M3（x3，y3，z3）点，定义该部分光程长度为s2。根据费马原理，三部分光程之和为常数：

若主镜在子午方向产生了偏心平移失调，如图4所示，即沿着y方向平移了δ，入射光线IR入射到主镜镜面上的点的x轴坐标与y轴坐标不变，仍然为（x1，y1），但光线入射到主镜镜面上的点的z轴坐标平移了Δz1，此时入射光线与主镜镜面交点的坐标为M′1（x1，y1，z1+Δz1）。相应地，入射光线与次镜镜面交点的坐标也发生了变化，为M′2（x2+Δx2，y2+Δy2，z2），其中z2是x与y的函数。

主镜位置产生偏心平移失调后，光线经光学系统的3部分光程之和为：

图4 主镜偏心平移后的光线追迹Fig.4 Ray tracing in condition of PM decenter

这里需要强调的是，在反射式光学系统敏感度影响因素的理论分析中，关注的是光学系统在无补偿情况下由光学元件失调导致的光程变化的敏感度，在一定程度上这种敏感度表征了光学系统对光学元件扰动的抵抗能力，所以在分析时，焦面位置保持不变，即系统无调焦补偿环节。

对比式（6）与式（5）的变化量可知，在主镜产生偏心平移失调前后，光学系统OPV为：

在式（7）中，对Δz1进行数学展开［19］，得到：

为了便于简化，这里对式（8）利用一阶近似，则有：

在考虑式（7）中的Δs1与Δs2时，首先分析光程s1与光程s2。根据空间两点之间的距离公式得到：

在假定条件下，z1，x2，y2的变化会影响s1的数值，则利用一阶近似，光程s1的变化量为：

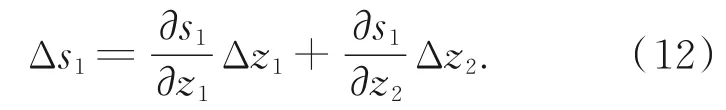
这里z2的变化以函数的形式体现在x2与y2中，则有：

同理，光程s2的变化量为：

综合分析式（13）与式（14），首先归纳分析得到：

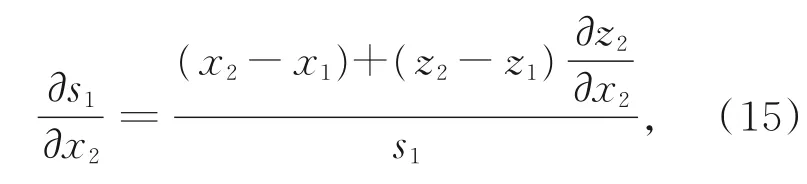
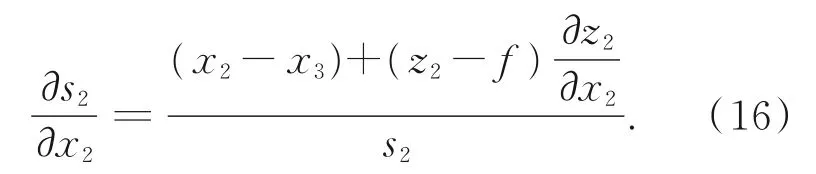
如图5所示，光线在光学系统中传播时，以光轴为回转对称轴，光线与每个光学元件相交的坐标点相对x坐标轴与y坐标轴具有相同的辐角数值，且光线与光学元件相交点的坐标为：

式中：r为相交坐标点的孔径值，是该点距离光轴的径向距离；x为相交坐标点在x轴的坐标；y为相交坐标点在y轴的坐标；θ为辐角值。

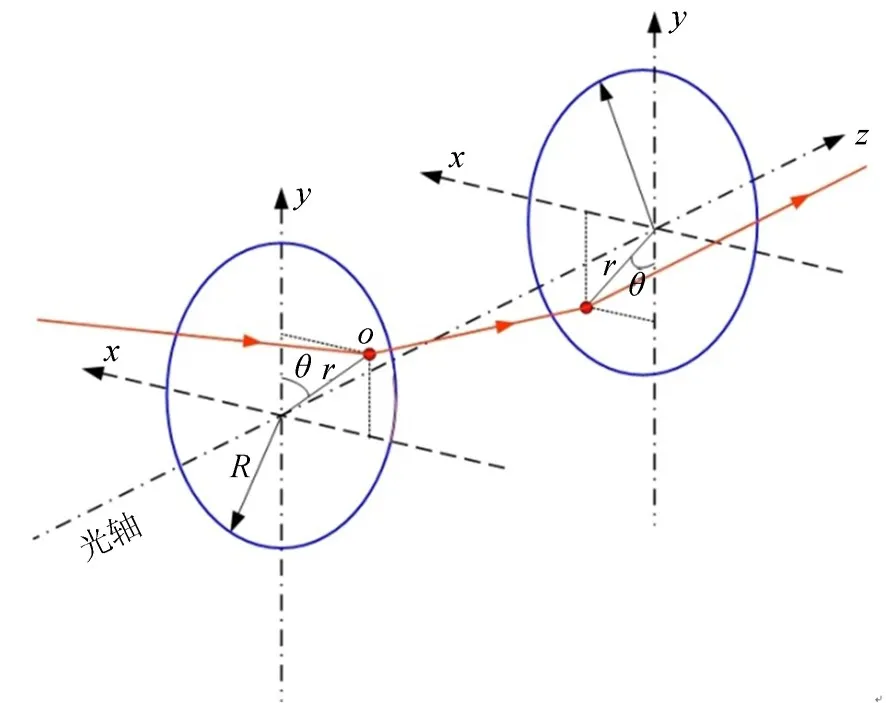
图5 空间光线传播示意图Fig.5 Ray propagation in three-dimensional space

所以在光学系统中，有：

因此有：

为了求解式（19），在图3的基础上，在光学系统模型中增加一些特殊角度，如图6所示。

图6 光学系统结构模型Fig.6 Configuration model of optical system

根据反射定律，入射光线与反射光线分居法线两侧，入射角等于反射角，当入射光线交主镜于M1点时，定义法线为NL，入射角为φ；以光线与次镜镜面交点M2为一点，定义与入射光线平行的直线PL，直线PL与光线S1的夹角则为2φ，直线PL与光线S2的夹角为ξ，ξ是光学系统像方孔径角的1/2。根据定义有：

如图7所示，z2为曲面矢高，是次镜的曲面函数；r2如式（4）所述，是曲面投影在x轴与y轴确定的平面上的点相对于光轴的径向距离，曲面z2上任意一点处的切线为TL，法线为NL。z2曲面沿着r2方向的偏导数为：

式中ζ为次镜曲面上任意一点处的法线与直线PL的夹角。

如图7所示，曲面矢高z2的增长与径向距离的增长符号相反。根据次镜的入射光线、反射光线、法线和曲面切线等特征线构成的角度数学关系，则有：

图7 光线路径数学关系Fig.7 Ray propagation mathematical model

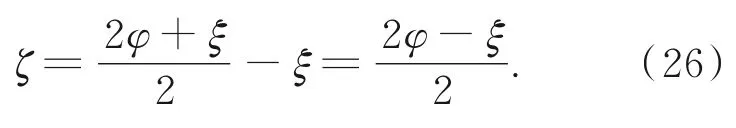
根据式（25）与式（26）即可得出式（24）。

将式（20）～式（24）代入式（19），则有：

即有：

根据以上数学关系可知，主镜偏心平移扰动给光学系统带来的OPV为：

式中：

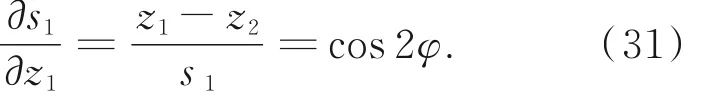
假设主镜在子午方向产生了偏心平移失调，即沿着坐标轴y方向平移了δ，所以有：

则式（31）可转化为：

大型反射式光学系统，如哈勃空间望远镜、詹姆斯·韦伯太空望远镜等，多属于长焦距小相对孔径系统，主镜焦比较小，则光线在主镜上的入射角与反射角φ也较小［20］。以哈勃空间望远镜为例，主镜光线入射角φ约为6°［21］。因此，根据一阶近似可以认为：

综上分析，由主镜偏心平移失调引起的OPV如下：

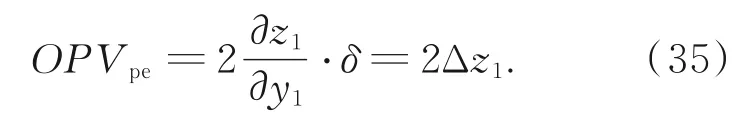
在两镜光学系统中，当主镜沿着子午方向产生了偏心平移失调量δ，对任意一根光线所产生的OPV，为该光线与主镜镜面入射点处的镜面矢高z沿y方向的变化率（偏导数）与2倍偏心平移失调量δ的乘积，也为失调前后该光线在主镜镜面入射点处矢高变化量的2倍。这个结论不仅适用于主镜沿子午方向平移产生的失调，还适用于主镜沿着任意方向产生的平移失调。

2.3 次镜偏心平移失调

根据前一节对主镜平移的失调推导，当次镜产生偏心平移时，由次镜偏心平移引起的光学系统OPV为：

同前文推导结论一致，在两镜光学系统中，当次镜沿着子午方向产生了偏心平移失调量δ，对某一光线所产生的光程变化量OPV，为该光线与次镜镜面入射点处的镜面矢高z沿y方向的变化率（偏导数）与2倍偏心平移失调量δ的乘积，也为失调前后，该光线在次镜镜面入射点处矢高变化量的2倍。这个结论不仅适用于次镜沿着子午方向平移产生的失调，还适用于次镜沿着任意方向产生的平移失调。

通过对两镜反射式光学系统中主镜偏心平移与次镜偏心平移的数学推导可以看出，该结论可以推广到三镜反射式光学系统乃至多镜反射式光学系统中。

2.4 主镜、次镜倾斜失调

当主镜或次镜发生倾斜时，如图8所示，光程长度z1，s1与s2的变化因素与前文推导过程完全一致。因此，可直接利用前文推导结论，若主镜以顶点为圆心，绕着弧矢轴倾斜扰动了角度η，则入射到主镜上高度为y1的光线的OPV为：

同理，若次镜以顶点为圆心，绕着弧矢轴倾斜扰动了角度η，则入射到次镜上高度为y2的光线的OPV为：

式中：y1与y2表征光线与镜面交点处的位置坐标，与关于主镜偏心平移的数学推导过程唯一不同的是对矢高变化量Δz的表征方式不同。

在两镜系统中，当主镜绕着弧矢轴倾斜扰动了角度η，对某一光线所产生的OPV为失调前后该光线在主镜镜面入射点处矢高变化量的2倍，也为倾斜角度η与光线高度坐标乘积的2倍。这个结论不仅适用于反射镜绕着弧矢轴倾斜扰动，还适用于反射镜绕着任意方向产生的倾斜扰动。

图8 反射镜倾斜后的光线追迹Fig.8 Ray tracing in condition of mirror tilt

2.5 主次镜轴向距离失调

光学元件之间沿着光轴方向的距离变化是最为常见的位置误差，其最明显的影响是使光学系统产生离焦。如图9所示，简化式（10）与式（11），将光程s1与s2表示为：

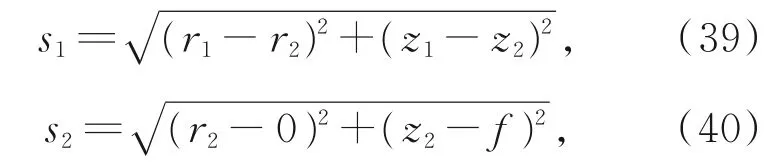
图9 主次镜轴向距离变化后的光线追迹Fig.9 Ray tracing in condition of mirrors distance pertur⁃bation

当主次镜轴向距离产生变化时，假设次镜向远离主镜的方向移动Δz2时，则在光学坐标系下有：

求解式中的偏导数部分得到：

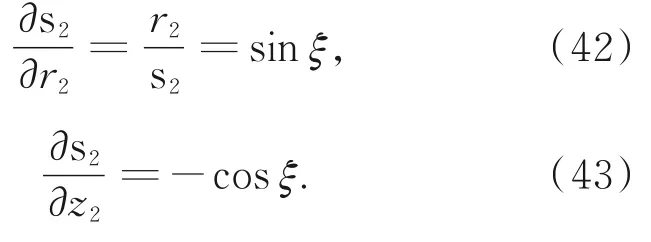
式中，三角函数的正负号关系可通过参数之间的变化关系得到，即当r2增大时，s2也随之增大，所以sinξ前为正号；当z2增大时，s2随之减小，所以cosξ前为负号。将式（42）与式（43）代入式（41）得到：

根据以上数学推导关系，由于主次镜轴向距离变化扰动给光学系统带来的OPV为：

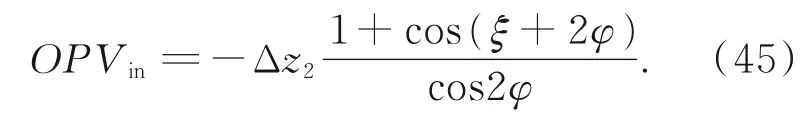
式中的负号表示：当主次镜轴向距离变大时，即Δz2取负值时，光程增大。

结合式（45）进一步分析，当ξ与2φ均较小时，cos（ξ+2φ）≈1，cos 2φ≈1，则有：

3 OPV光线追迹验证

为了验证2.2至2.5节中推导的由各种失调因素引起光学系统OPV的数学式，应用一个系统焦距为1 000 mm，相对孔径为1∶5的标准Ritchey-Chrétien系统进行光线追迹，对光学系统分别施加主镜偏心平移、次镜偏心平移、次镜倾斜和主次镜轴向距离失调等扰动。采用光线追迹法对上光线的实际OP、由失调因素引起的上光线OPV进行计算，以（2Δz-OPV）/OPV评价OPV理论解析值与光线追迹真值的误差，结果如表1～表4所示。

分析结果显示，与OPV光线追迹值对比，主镜偏心平移、次镜偏心平移、主次镜轴向距离失调扰动引起的OPV的理论解析计算误差在1%量级；反射镜倾斜失调扰动引起的OPV的理论解析计算误差在0.1%量级，验证了理论分析结果的正确性。

表1 主镜偏心平移时光程变化量的数据分析Tab.1 Data analysis of OPV for PM decentration condition

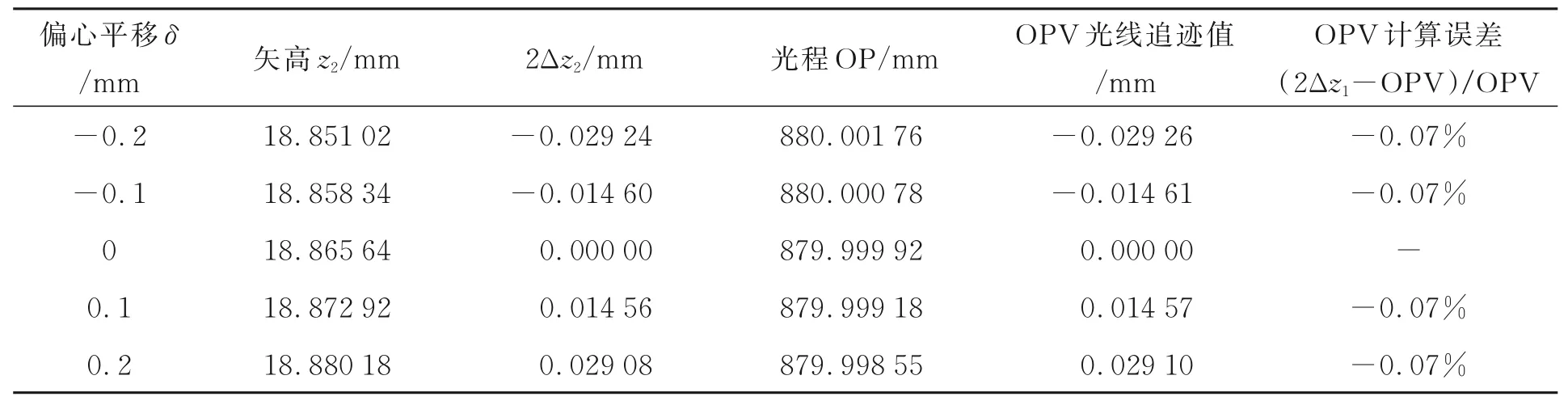
表2 次镜偏心平移时光程变化量的数据分析Tab.2 Data analysis of OPV for SM decentration condition

表3 次镜倾斜时光程变化量的数据分析Tab.3 Data analysis of OPV for SM tilt condition

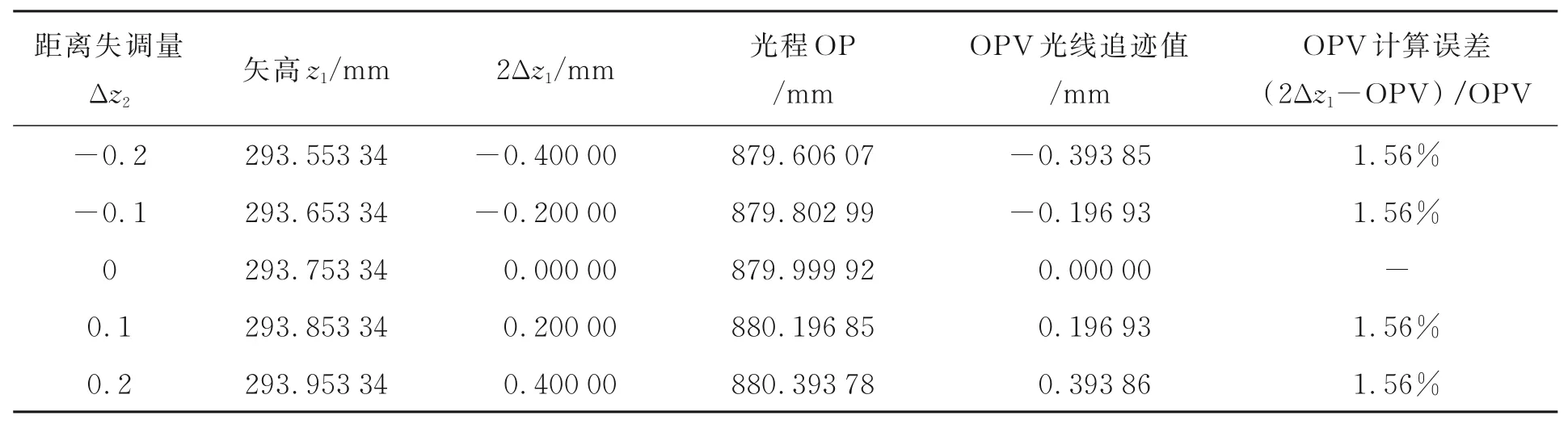
表4 关于主次镜轴向距离变化的光学系统光程变化量的数据分析Tab.4 Data analysis of OPV for mirrors distance perturbation condition

4 基于光程变化量的降敏设计

4.1 降敏设计

评价函数是光学系统设计的重要评价指标。当光学系统受到相同的失调扰动时，OPV大的光学系统，敏感度高，鲁棒性差；OPV小的光学系统，敏感度低，鲁棒性好。

由多种因素引起的OPV具有独立性和互不相关性，可以采用和方根值（Root-Sum-Squares，RSS）来计算由于多种失调因素引起的总的OPV。因此，将式（47）作为评价函数来对光学系统进行降敏设计，相关各种其他失调因素引起的OPV可进行数学理论推导。

基于该思想与OPV评价函数，设计了一个焦距为5 600 mm，相对孔径为1∶7，视场角为15′的两反系统。设计过程中对系统OPV进行约束，以达到降敏设计的目的，使它在多项失调公差约束的情况下，以8.200 0μm作为系统OPV判定的上限阈值。像质判定标准则选用波前误差（Wavefront Error，WFE）RMS平均值，判定阈值为0.065 0λ（λ=0.48μm）。

通过初始结构筛选，经过15轮迭代优化设计（光学系统结果标记为L1～L15），获得了RMS波像差为0.059 85λ、OPV为8.195 6μm的光学系统。该光学系统的OPV与RMS WFE值的变化曲线如图10所示。

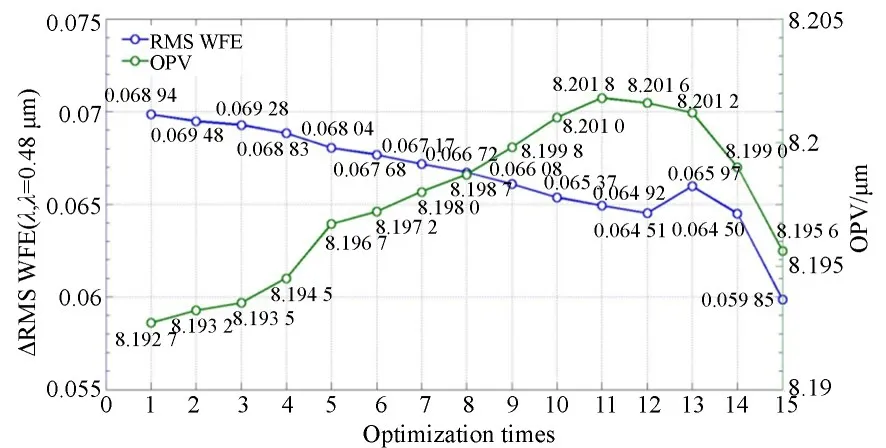
图10 降敏优化过程中RMS WFE与OPV的变化Fig.10 Variation of OPV and RMS WFE in desensitiza⁃tion optimization process

4.2 评价函数OPV与波像差改变量（ΔRMS WFE）的关系

商业光学系统设计软件没有直接计算OPV的功能。通常，设计人员通过计算在特定公差下的波像差改变量（ΔRMS WFE），来判断光学系统的敏感度情况。根据波动光学理论，OPV与ΔRMS WFE的数学关系可表示为：

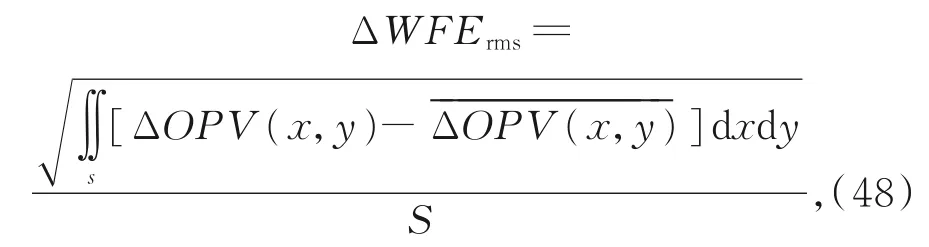
式中S为光瞳面积。

从式（48）中并不可直接获知OPV与ΔRMS WFE的相关性。在降敏设计过程中，从实验数据角度，为了验证OPV评价标准的正确性，与基于OPV的降敏设计方法的有效性，同步计算了15轮迭代设计过程中的ΔRMS WFE。通过实验数据可以看出，光学系统OPV与ΔRMS WFE具有正相关性，在优化过程中，二者的变化趋势一致。

图11 降敏优化过程中光学系统ΔRMS WFE与OPV的变化情况Fig.11 Variation of OPV andΔRMS WFE in desensiti⁃zation optimization process

综上分析，从波像差理论与实验数据两方面，验证了OPV评价标准的正确性与基于OPV评价标准的光学系统降敏设计方法的有效性。OPV与ΔRMS WFE均可以在光学设计中作为评价光学系统敏感度的评价标准。

5 结 论

基于失调后成像光线的光程变化绝对量越小，成像质量退化也越小的思想，本文提出以OPV作为衡量光学系统敏感度的评价标准。在一阶近似的条件下，通过建立光线传播路径的几何模型，理论推导了主镜/次镜偏心、主镜/次镜倾斜、主次镜间距变化等误差因素引起的OPV的数学解析表达式。通过一套标准Ritchey-Chretien系统，应用经典几何光线追迹法，计算了在各种失调扰动情况下所产生的OPV实际数值，与理论推导值对比，相对误差均在1%左右，证明了所推导的OPV理论表达式的正确性。

基于OPV的理论推导，建立了以OPV为评价函数的反射式光学系统降敏设计方法，设计了一个焦距为5 600 mm，相对孔径为1∶7，视场角为15′的两反系统，经过15轮迭代设计，获得了OPV与RMS WFE均满足指标要求的系统。对设计过程数据进行监控，分析了15轮迭代设计过程中的OPV与ΔRMS WFE，结果显示二者在优化过程中变化趋势一致，具有正相关性，验证了OPV评价标准的正确性与基于OPV评价标准的光学系统降敏设计方法的有效性。