感应电机基于最大转矩输入功率比的能效优化

（沈阳工业大学电气工程学院，辽宁 沈阳 110870）

工业和农业生产中大部分的负载由感应电机拖动，在工业部门中，超过70%的能量由感应电机转化为机械能，感应电机效率提升带来的节能效果和环境效益也非常可观[1]。此外，近年来电能成本的增加，愈加重视电机的能效运行。设计和研制高能效的电机可以替代传统低效电机进行生产[2-3]，而高能效电机的设计和制造只考虑额定运行，忽略了电机负载变化的情况。因此，即使应用高效的电机，在运行的过程中仍有较高的功率被损耗[4]。电机损耗的2个主要组成部分即铜损耗和铁损耗之间的不平衡，是电机运行过程中产生损耗的主要原因[5]。因此，电机能效优化控制策略的研究是非常必要的。

电机能效优化的原理主要有两种。一种是选择最优磁通来重建铜、铁损耗之间的平衡，据此原理提出了两种控制策略：基于损耗模型的损耗模型控制方法（loss model controller，LMC）和基于输入功率在线搜索控制（search controller，SC）[6-7]方法。LMC通过导出电机的损耗模型，分析电机效率与最优磁通值的函数关系，由该函数决定最优磁通的给定，从而实现电机的损耗最小化。损耗模型法需要精确的电机参数，以电机效率为优化目标，只能实现损耗功率的部分最小化，并非能效最优。SC是当电机的负载一定时，将励磁的给定作为控制参数，按一定的步长变化，直到输入功率最小化为止。SC需要监测输入功率、选择步长以及反复调整励磁给定，存在效果不佳、实现困难等缺点。另一种则是通过重新分配d，q轴的电流分量，来重建铜、铁损耗之间的平衡，提出了最大转矩电流比（maximum torque per ampere，MTPA）的控制策略。MTPA在电机模型的基础上，解析转矩与d，q轴电流的函数关系，以一定负载转矩情况下电流最小化即转矩电流比最大化为目标，重新分配d，q轴的电流，实现电机能效优化的目的[8-9]。然而，MTPA忽略了铁损耗的存在，电机的运行状态并非能效最优。

综合这些方法的优点，提出了一种基于考虑铁损耗的数学模型进行分析，以一定负载转矩条件下输入功率最小化为目标，重新分配d，q轴电流，减小电机损耗进而实现电机的能效优化方法，称之为最大转矩输入功率比（maximum torque per input pow⁃er，MTPIP）。结合转子磁场定向，将新方法应用于感应电机的矢量控制系统中。考虑铁损耗电阻会导致电压解耦和磁链观测器产生误差，重新设计了考虑铁耗的电压解耦方法和转子磁链观测器。

1 MTPIP控制策略的提出

1.1 感应电机考虑铁耗的动态数学模型

传统的感应电机动态数学模型忽略铁耗的影响，仅以互感电感并联表示励磁支路。建立考虑铁损耗的数学模型，有将铁损耗电阻与互感电感串联或者并联的方式[10-11]。文献[12]指出，若采用串联的方式，会得到ird≠0的结论，不符合转子磁场定向的原理，且并联的方式更能反映电机损耗的变化规律。在d-q坐标系中，感应电机考虑铁耗的动态数学模型如下[13]。

电流方程：

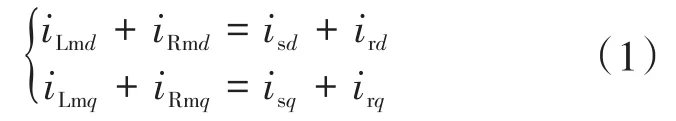
电压方程：

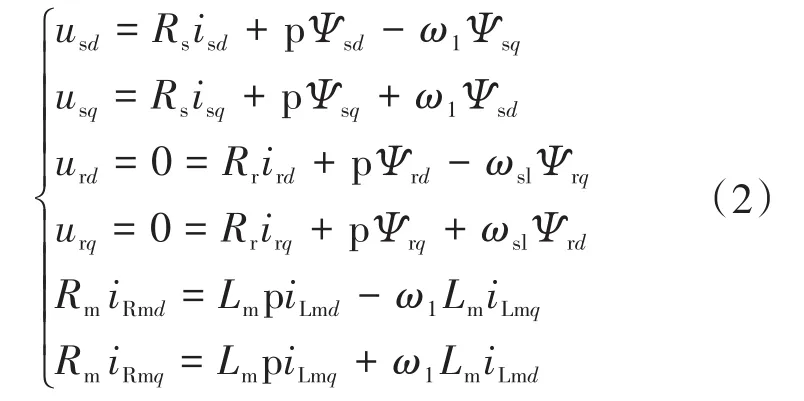
磁链方程：

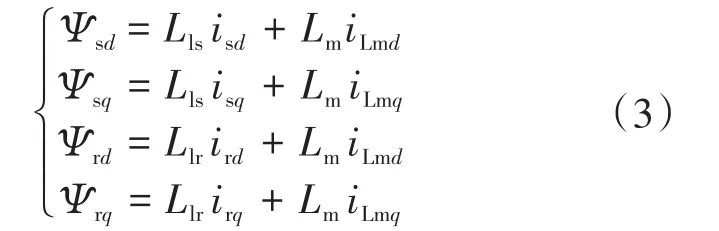
电磁转矩：

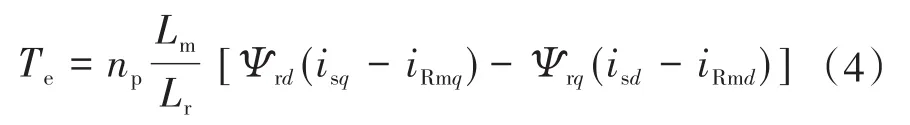
式中：p为微分算子；ω1为同步转速；ωsl为转差；Rs，Rr，Rm分别为定、转子电阻及铁耗电阻；Lr，Lm分别为转子自感及互感；Lls，Llr分别为定、转子漏感；isd，isq，ird，irq分别为 d，q轴的定、转子电流；iR⁃md，iRmq分别为 d，q轴铁耗等效电流；iLmd，iLmq分别为 d，q轴励磁电流；usd，usq分别为 d，q轴定子电压；Ψsd，Ψsq，Ψrd，Ψrq分别为定、转子d，q轴磁链；np为电机极对数。

考虑铁损耗的动态数学模型中，铁损耗电流为新的电机矢量，与定子电流耦合，为将转矩和输入功率用定子电流表示，需要先解耦。

当电机处于稳态运行并且转子磁场定向时，有：Ψrq=0和p=0，代入电机的数学方程中，可得：

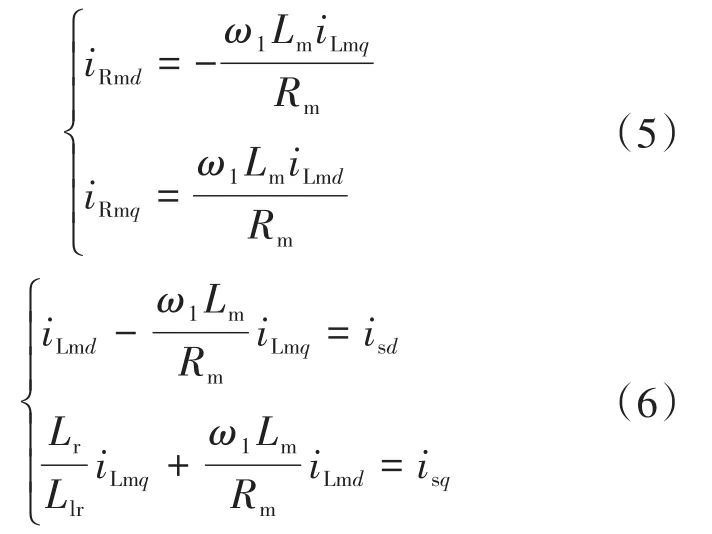
由式（6）得励磁电流关于定子电流的表达式：

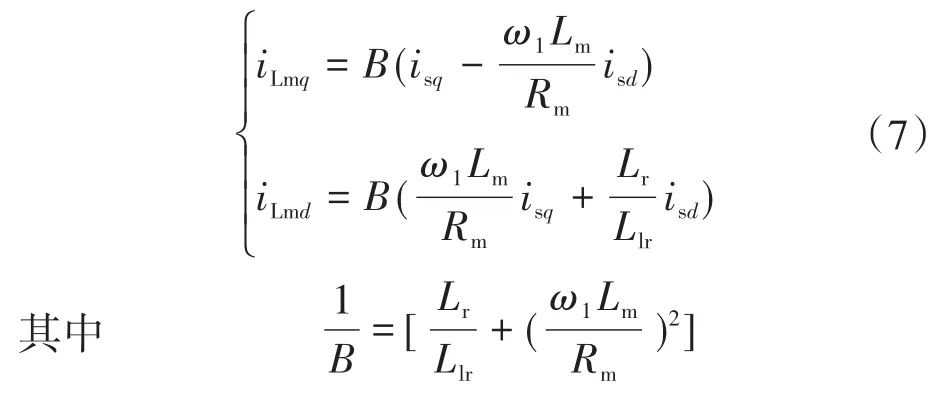
由式（7）可以发现，经过解耦后，励磁电流和铁损耗电流可由定子电流表示，为后文能效优化控制策略的提出奠定基础。

1.2 MTPIP控制策略

MTPIP控制策略为在恒定负载转矩的约束条件下，实现输入功率最小化的控制策略。因此，选择输入功率为优化目标。基于拉格朗日定理，可以发现，当转矩曲线和优化目标在某点处相切时，即梯度向量平行时，电机的能效达到最优点。在输出功率一定时，使输入功率最小化来实现能效最优。MTPIP控制策略需用定子电流表示转矩和输入功率。将式（6）代入转矩方程，得到转矩与iLmd,iLmq的关系式：

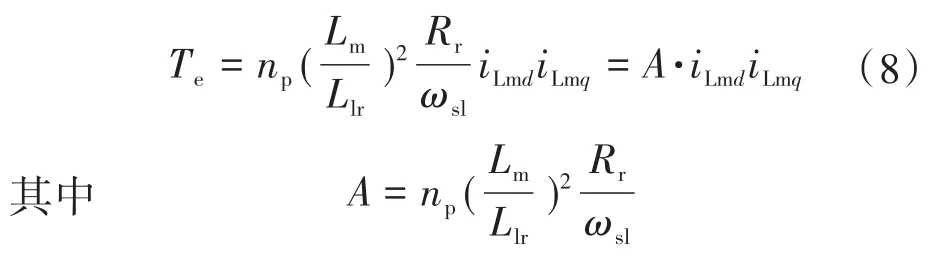
感应电机的输入功率Pinput可以表示为

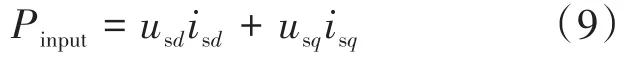
定子电压又可以表示为

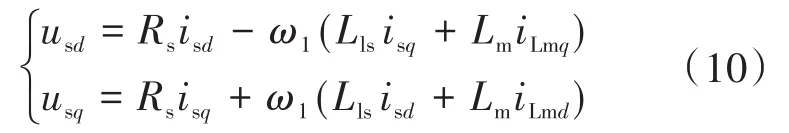
于是输入功率为

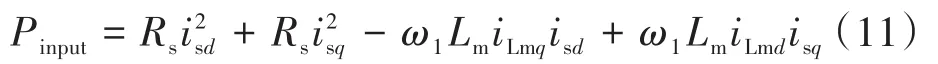
根据式（7）、式（8）可以在isd-isq平面上画出考虑铁耗的转矩方程。在同一平面上，根据式（11）得到输入功率的曲线，如图1所示。恒转矩条件下，若工作点为a，曲线A为恒转矩下输入功率的曲线（Pinput，a），若工作点为b，则曲线B为另一条恒矩阵下输入曲线（Pinput，b）。根据拉格朗日定理，可以发现，两条曲线相切时（∇Te和∇Pinput平行），输入功率最小（参见图1中的b点）。

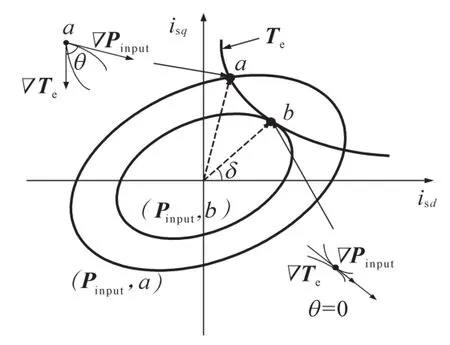
图1 isd-isq平面上转矩曲线和输入功率曲线Fig.1 Torque curves and input power curves on the isd-isqplane

∇Te和∇Pinput平行，即当且仅当：

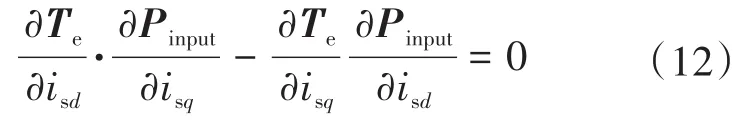
计算转矩和输入功率对d，q轴电流的偏导并代入式（12），且令X=isd/isq，简化得：

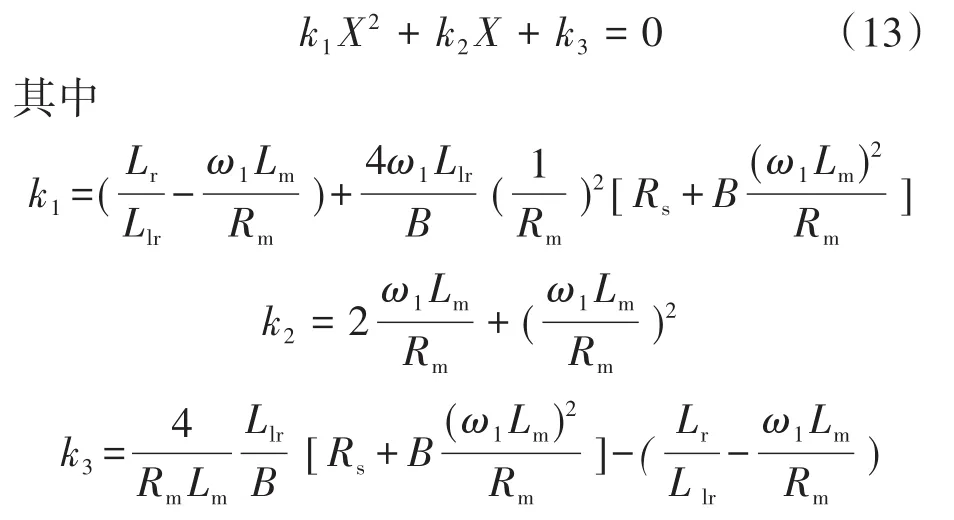
由式（13）可以看出，最大转矩输入功率比与d，q轴电流的比例系数X相关，MTPIP能效优化的实质，为对d，q轴电流分量的分配。而isq为转矩分量，不宜调整；isd为励磁分量，因此通过调整isd，可以实现感应电机的能效优化。式（13）的解为

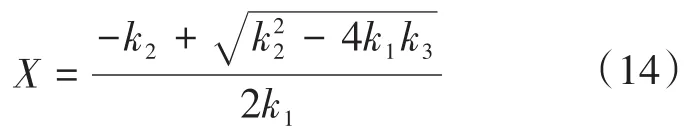
由于电机空载时，q轴电流非常小，导致计算的isd近似为零，需要限制isd的最小值I1，同理，电机重载时会超过额定值I2，于是isd的给定为

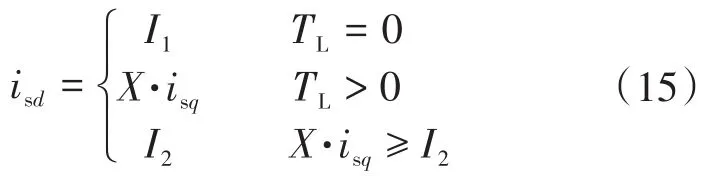
2 考虑铁耗的矢量控制系统

2.1 考虑铁耗的电压解耦方法及磁链观测器

感应电机驱动系统采用电压源型逆变器，需要将d，q轴的控制量——电流转换成电压的控制量，而d，q轴电压之间存在耦合[14]。文献[15]提出了一种解耦方法，并未考虑铁损耗，根据式（7）、式（10）可以得到新的解耦方法。

设置usd-pu，usq-pu为电压解耦补偿，则

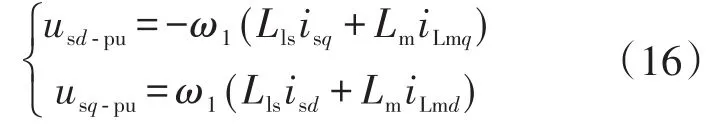
由于铁损耗Rm的磁通观测器会不可避免地产生误差，进而会影响到系统的控制性能。为了解决这个问题，需重新设计考虑Rm的磁通观测器。结合式（11）与电机的数学方程可得：

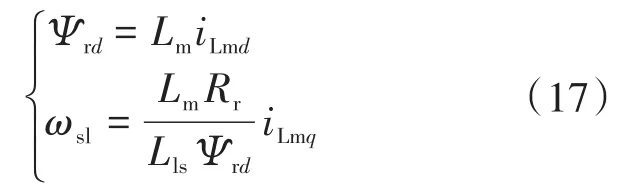
转差计算为

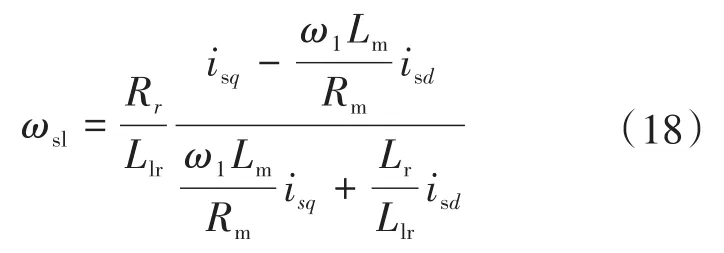
MTPIP能效优化控制策略与矢量控制系统相结合，系统原理示意如图2所示。

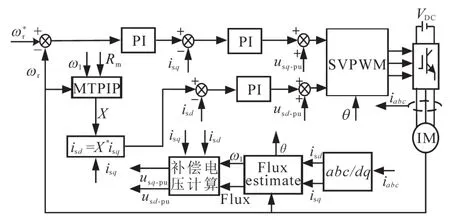
图2 基于MTPIP的感应电机矢量控制系统原理示意图Fig.2 Schematic diagram of induction motor vector control system based on MTPIP

在图2中，转速作为系统的给定，与实际值做差后，经转速PI调节器，输出q轴电流给定，与定子电流解耦后的q轴电流实际值求差后，经转矩PI控制器得到q轴电压的给定。将转速实际值、计算的ω1和铁损耗电阻Rm输入MTPIP中，计算比例系数X，X与q轴电流实际值相乘，得到励磁电流的给定，经励磁PI调节器后，得到d轴电压给定。SVPWM根据电压给定，输出逆变器的驱动信号，逆变器输出正弦电流驱动电机，使得电机达到设定的运行状态。补偿电压可根据式（7）、式（16）计算，磁通观测器可以根据式（17）以及式（18）设计。

2.2 控制系统的仿真模型

根据图2中设计的系统控制原理图，在Simu⁃link仿真平台上搭建控制系统的仿真模型。模型库中没有考虑铁损耗的感应电机仿真模型，需要根据上文中提出的数学模型自行搭建，仿真模型如图3所示。以一台7.5 kW的感应电机为例，验证MTPIP控制策略的能效优化效果。

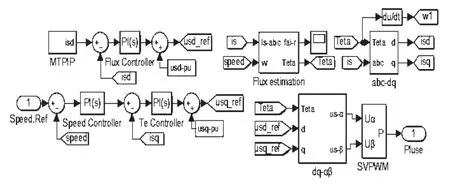
图3 基于MTPIP的矢量控制系统仿真模型Fig.3 The simulation model of vector control system based on MTPIP

仿真模型中电机参数设置为：PN=7.5 kW，UN=380 V，Rm=46.63 Ω，J=0.05 kg·m²，np=2，Rs=0.332 Ω，Rr=0.153 Ω，Lls=0.001 H，Llr=0.001 H，Lm=0.061 5 H；PI控制器的参数设置如表1所示。

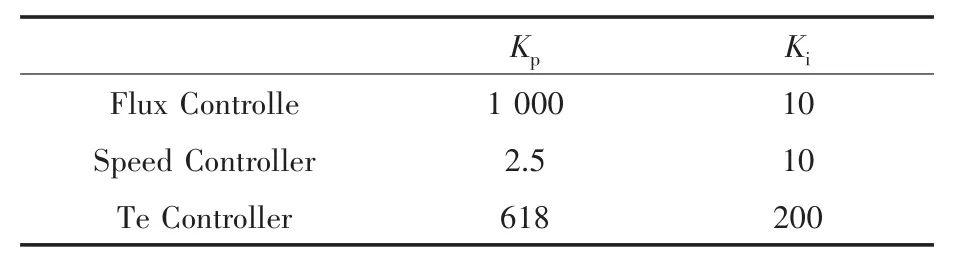
表1 控制器的PI参数表Tab.1 PI parameter table of the control system

3 仿真结果及其分析

图4、图5分别为转速、转矩的仿真结果。分析图4、图5仿真波形可知：电机快速启动并达到稳态时，转速达到给定值，当转矩给定发生改变时，仍能保持为给定值；当电机转速的给定发生了改变，电机的运行状态发生改变，输出转矩受到影响产生突变，但因为转矩给定不变，输出转矩立刻恢复到给定值。由此可见，考虑铁损耗的矢量控制系统具有抗干扰能力强、稳定性好等优点。

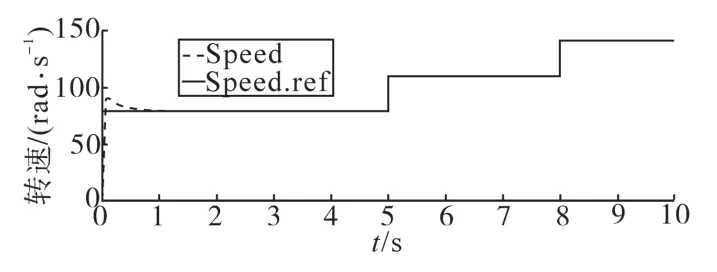
图4 转速的仿真结果Fig.4 Simulation results of the speed

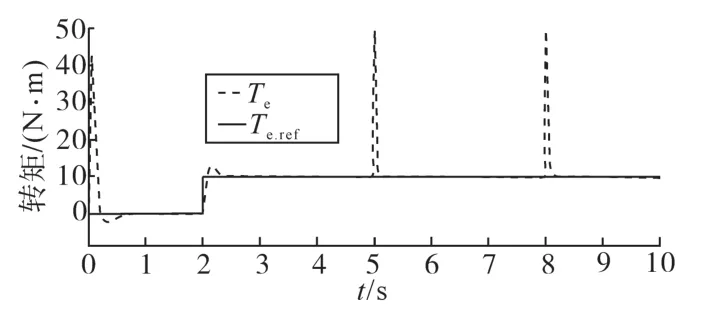
图5 转矩的仿真结果Fig.5 Simulation results of torque

图6为损耗功率的仿真结果图。在图6中，虚线为MTPIP的损耗功率变化，实线为恒磁通控制的损耗功率变化。可以看出，稳定运行时，虚线一直在实线下方，即MTPIP方法可以有效地减少电损耗，提高电机的能效水平。具体来说，转矩为空载、转速为80 rad/s时，损耗功率分别为700 W和320 W；转矩为10 N·m、转速为80 rad/s时，损耗功率分别为700 W和580 W；在仿真转矩为10 N·m、转速为110 rad/s时，损耗功率分别为920 W和700 W；在仿真转矩为10 N·m、转速为140 rad/s时，损耗功率分别为1 150 W和850 W；可见MTPIP的能效优化效果明显。

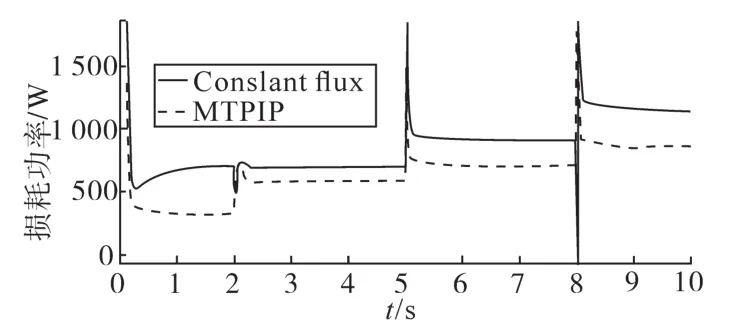
图6 损耗功率的仿真结果图Fig.6 Simulation results of loss power

4 结论

针对感应电机运行在非额定条件下能效不高的问题，在考虑损耗模型的基础上，结合MTPA弱磁控制策略，提出一种新型的损耗功率最小化的方法，即MTPIP能效优化方法。该方法通过计算转矩向量和输入功率向量的梯度为零，即转矩和输入功率比最大化时的d，q轴电流的比例系数X，根据这个比例系数重新在线调整励磁电流的给定值，提高感应电机运行的能效水平。此外，考虑到了铁耗的影响，在考虑铁耗的感应电机数学模型基础上，提出了考虑铁耗的磁通观测器设计和电压解耦方式，并将其应用于转子磁场定向的矢量控制系统中。通过对一台7.5 kW感应电机的仿真实验，验证了所提出的MTPIP控制策略以及矢量控制系统，不仅可以提高感应电机运行的能效水平，而且不影响系统动态性能。