基于有限元及灰色度分析的地铁隧道施工地表沉降预测研究

田 超

（中铁十八局集团第一工程有限公司，河北涿州 072750）

1 引言

我国地铁建设不断发展，大量的地铁隧道正在建设中，隧道施工对地表沉降及地表建筑物安全有严重影响。因此，地铁隧道施工地表沉降预测已成为目前亟需解决的问题。文献[3]提出隧道管幕支护施工地表沉降预测方法，该方法为基于随机介质理论建立考虑地层损失和施工应力的单管顶进施工地表沉降计算方法，通过群管施工地表沉降修正函数进行修正，并通过FLAC3D数值模拟进行验证，该方法在使用过程中敏感度较差，无法对地表沉降数据激增情况进行预测；文献[4]提出基于LIB-SVM（支持向量机算法）的盾构隧道地表沉降预测方法，该方法通过交叉验证选取LIB-SVM的最优参数组合并建立预测模型，对盾构施工引起的地表沉降进行了预测，该方法的预测结果误差较大，导致预测能力较差。

针对上述方法存在的问题，本文提出基于有限元分析及灰色度分析的地铁隧道施工地表沉降预测方法，以期弥补现有预测方法在使用中的不足，进一步确保地铁施工和地面建筑物安全。

2 隧道施工地表沉降预测

本文根据地铁隧道施工的特征与要求，选用MADIS-GIS有限元分析应用软件构建隧道三维有限元模型，对地铁隧道施工地表沉降进行分析，在有限元分析数据基础上，应用灰色度理论提出地铁隧道施工地表沉降预测方法。

2.1 地表沉降有限元分析

地表沉降三维有限元模型构建中，为便于后续的计算与处理，将模型尺寸设定为50 m×10 m×10 m，模型边界在位移结束后可使土体的水平移动限制为零，上边地表为自由运动边界；通过网格的形式体现有限元模型划分结果，模型中共有节点42 514个，单元42 600个；使用“生死单元”原理，合理利用模型中的各因素，对模型进行分析处理，最终得到地表沉降有限元分析结果 。地表沉降隧道三维有限元模型如图1所示，模型中包含的地层与材料物理参数如表1所示。

进一步将有限元分析得到的地表沉降数据按式（1）进行转化采集，以作为灰色度分析基础数据。

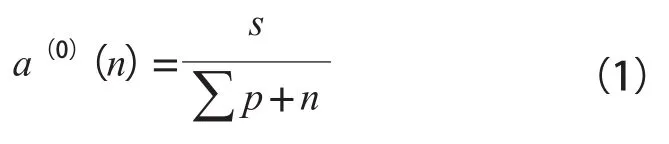
式（1）中，a（0）（n）表示地表沉降有限元分析数据；表示有限元分析数据中脏数据处理结果；n表示数据量；s表示数据统一格式参数。

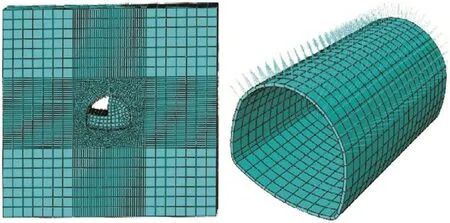
图1 地表沉降隧道有限元模型

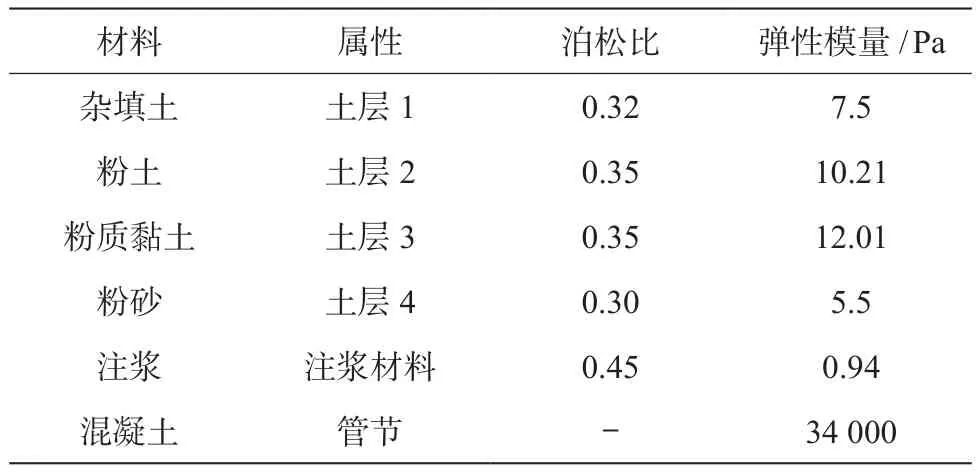
表1 有限元模型所需参数

2.2 地表沉降预测

在上述地表沉降有限元分析数据及转化采集数据的基础上，结合灰色度GM（1，1）模型，对地表沉降量预测方法进行研究。设定有限元分析转化数据中得到的非负序列为A（0），则A（0）可表示为：

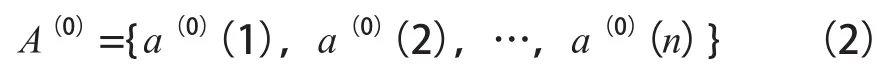
式（2）中，a（0）（1），a（0）（2），…，a（0）（n）表示非负序列值。

以A（1）表示A（0）的显性特征序列1-AGO，则有：

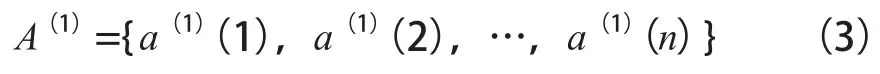
式（3）中，a（1）（1），a（1）（2），…，a（1）（n）均表示显性特征序列值。

以B（1）为A（1）的紧邻均值生成序列，则有：

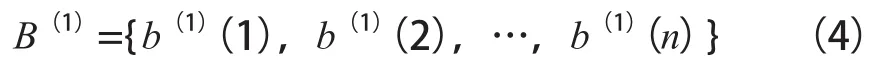
式（4）中，b（1）（1），b（1）（2），…，b（1）（n）均表示紧邻均值生成序列的序列值。

根据灰色度GM（1，1）模型，建立预测模型微分方程：

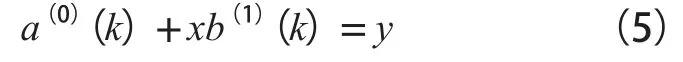
式（5）中，k=1，2，3，…，n；x表示预测模型微分方程参数；y表示预测模型微分方程解。

式（5）可通过最小二乘法完成求解过程，具体公式如下：

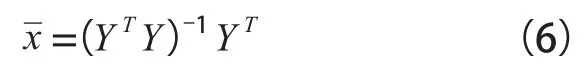
结合最小二乘法求解结果，得到此预测模型影子方程：

式（7）中，δ表示两模型之间的距离；t表示运算处理时间；e为预测模型影子方程解；γ为预测模型特征值。

对式（7）进行求解可得到预测模型的时间响应函数如下：

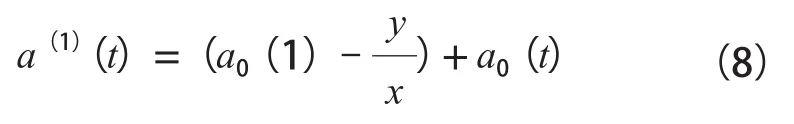
式（8）中，a0（1）表示时间响应初始特征值；a0（t）表示时间响应终止特征值。两特征值的差a0（t）-a0（1）即为预测沉降发生时间。

则预测模型微分方程的时间序列 可表示为：

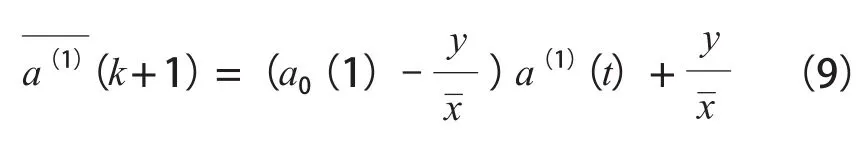
通过式（9）得到的预测时间序列即为预测沉降值。

为提升模型的预测精度，需要对其进行检验。根据此次预测方法的使用要求，使用残差法对其进行二次计算，设定模型残差为α（1）（k），其计算公式如下：

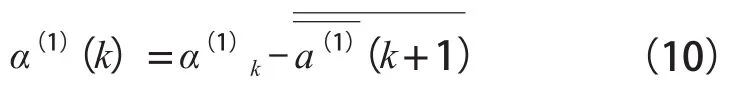
式（10）中，a（1）k表示时间响应k次特征值；表示时间序列集。

通过式（10），结合有限元分析得到的地表沉降数据a（k），计算得到其均值a-（0（）k）：

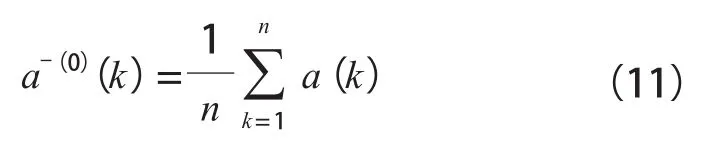
通过式（12），可验证模型预测结果的真实性与可靠性。将通过式（12）计算得到的残值均值及其残差误差划分成4级，如表2所示，据此对预测结果进行划分，以提升地表沉降预测结果。至此，基于有限元分析及灰色度分析的高速铁路隧道施工地表沉降预测方法设计完成。

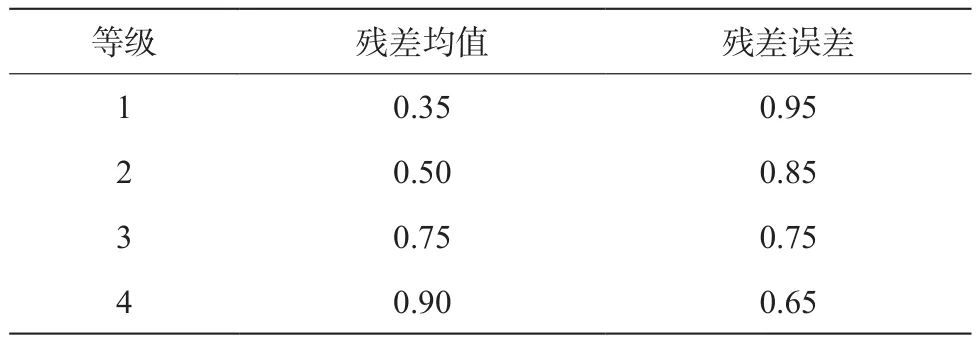
表2 预测结果检验等级

3 实验分析

3.1 实验数据样本

为验证本文基于有限元及灰色度分析的地铁隧道施工地表沉降预测方法（简称为“本文预测方法”）的预测效果，本文通过仿真实验对预设数据样本进行预测分析，并将本文预测方法分析结果与文献[3]提出的隧道管幕支护施工地表沉降预测方法（预测方法1）和文献[4]提出的基于LIB-SVM的盾构隧道地表沉降预测方法（预测方法2）所得结果进行实验对比。实验以某新建隧道中5个测试断面作为数据样本，5个测试断面信息如表3所示。

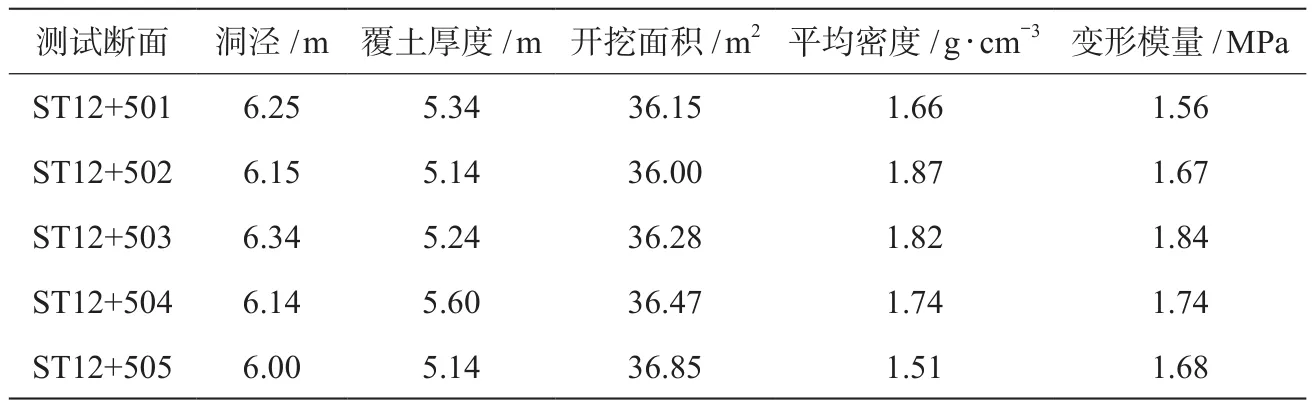
表3 隧道测试断面信息

3.2 实验结果分析

（1）实验分析中，地表沉降实测值、预测值、残差均值、残差误差的分析结果如表4所示。表4实验结果可以看出，本文预测方法所得到的残差均值、残差误差接近表2预测结果检验等级的1级，且均优于预测方法 1与预测方法2 得到的残差均值、残差误差，表明本文预测方法所预测的结果精准度与可靠性均较高。

（2）表5 给出了地表沉降发生时间实验结果分析，由表5实验结果可知，本文预测方法所得到的沉降发生时间预测结果与实测结果一致，而预测方法1与预测方法2的沉降时间预测结果具有一定的滞后性，与实测结果相差较大，这表明本文地表沉降时间预测效果优于目前使用中的地表沉降预测方法1与预测方法2。

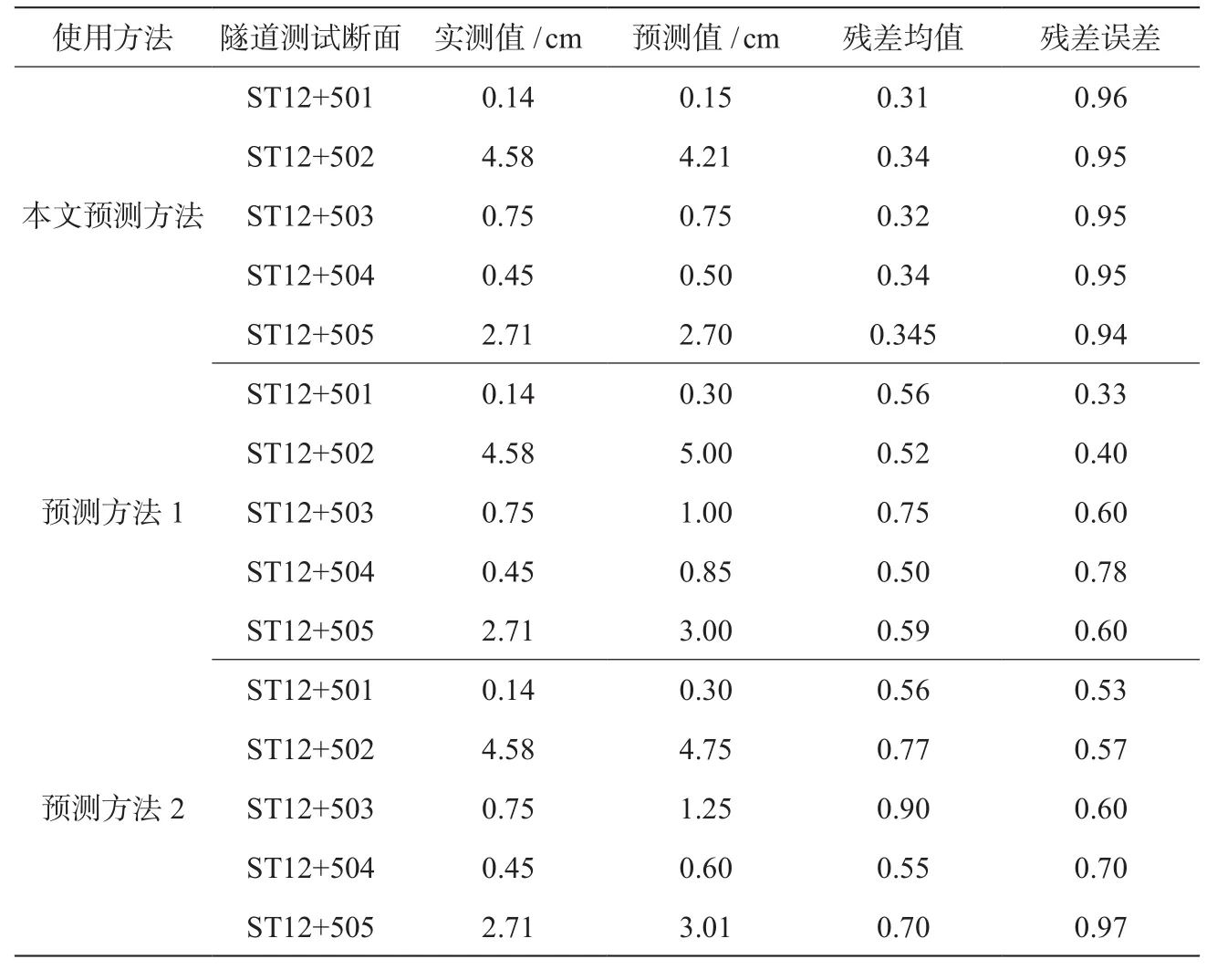
表4 地表沉降实测值、预测值、残差均值、残差误差分析结果

4 结束语

本文针对地铁隧道施工地表沉降问题进行研究，选择有限元和灰色度分析法对地铁隧道施工地表沉降进行预测。实验分析表明，本文提出的地铁隧道地表沉降预测方法（本文预测方法），在地表沉降预测误差以及时间等方面的预测与应用效果均优于目前使用中的隧道管幕支护施工地表沉降预测方法（预测方法1）和 基于LIBSVM的盾构隧道地表沉降预测方法（预测方法2），能够有效预测地铁隧道施工地表沉降，可为地铁隧道施工和地表建筑物安全提供保障。

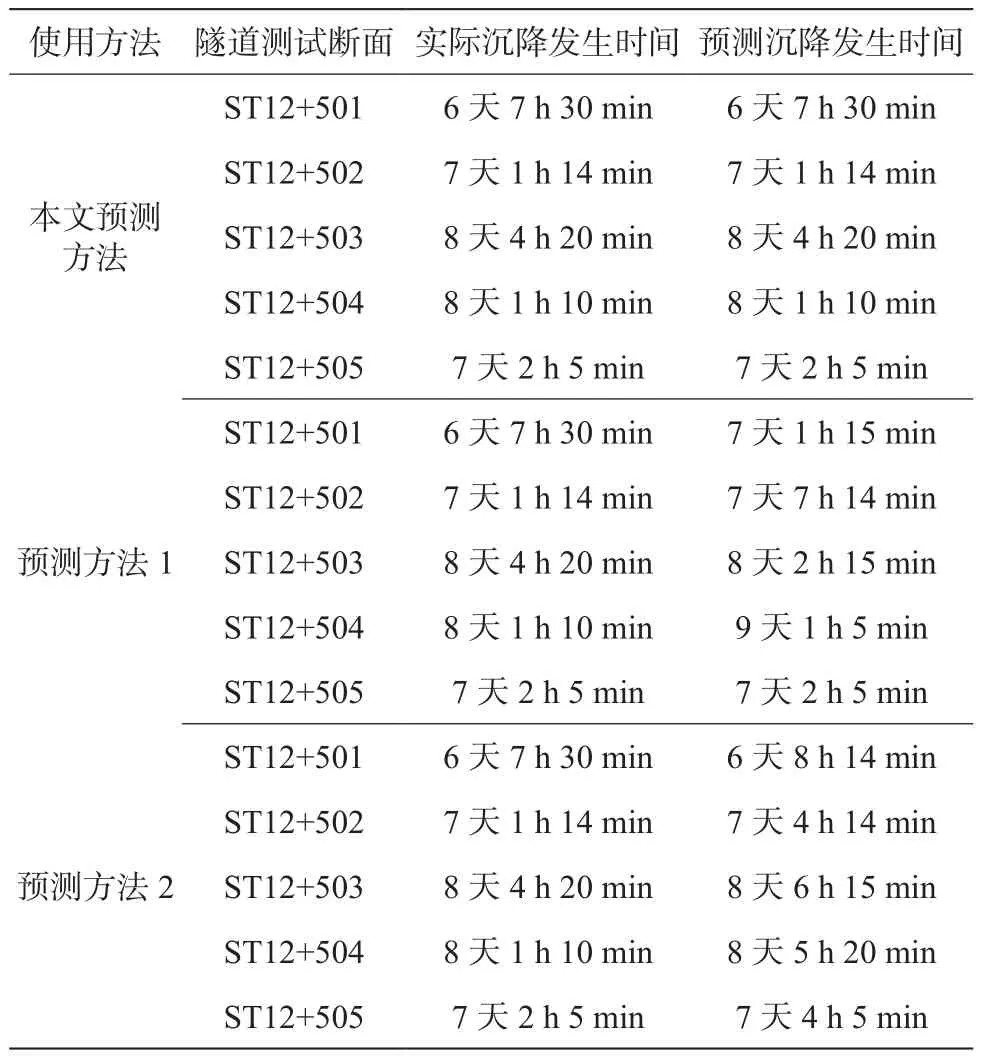
表5 地表沉降发生时间实验结果分析