产品生产定型可靠性试验方法研究
董理, 李宗吉, 周奇郑, 张志华
(海军工程大学, 湖北 武汉 430033)
0 引言
本文利用Bayes 方法建立了水雷产品设计定型阶段和生产定型阶段的可靠性信息转换模型, 借助该转换模型对批产品的各种先验信息进行综合,给出了生产定型可靠度的先验分布。 在此基础上,给出了生产定型可靠度验证试验方案制定方法,并进行风险分析, 最后通过实例说明了其可行性。
1 生产定型可靠性验证目标及影响因素分析
1.1 生产定型可靠性验证目标
从可靠性增长的角度来解释水中兵器产品从研制阶段到生产定型阶段再到批产阶段可靠性变化的一般规律。 在产品研制阶段, 随着试样、 初样和正样的逐步推进, 产品设计缺陷、 制造工艺缺陷、 零部件选用和操作方法缺陷等经过不断的试验、 分析和改进, 其可靠性逐步提高, 该阶段是可靠性增长的重要环节。 在研制阶段后期的设计定型阶段, 通过可靠性鉴定试验主要检验产品可靠性设计水平能够达到所规定的要求。
此后, 产品转入生产定型阶段, 该阶段初期由于产品生产工艺、 材料选用、 生产设施、 人员的操作技术与管理水平等方面都会存在许多问题,因此在生产阶段的初期, 虽然产品技术状态并未发生改变, 但其可靠度一般会有所下降。 随着生产过程的持续, 各个生产环节中存在的缺陷逐步地暴露, 生产设计人员不断采取针对性改进措施,质量控制水平不断提升, 使得产品的可靠性不断增长, 直到稳定地生产出满足可靠性规定要求的产品。 此后经过生产定型可靠性验证, 正式转入批产阶段。
因此, 从产品可靠性增长规律可以得出生产定型阶段可靠性验证的目的是: 在设计定型对产品可靠性设计水平检验的基础上, 进一步地检验生产工艺等质量控制对产品可靠性的影响, 最终确定能够稳定生产出满足军方可靠性规定的产品。
1.2 生产定型可靠性影响因素分析
与设计定型相比, 工装、 工艺等质量控制因素是生产定型任务可靠性的主要影响因素。 由此可见, 设计定型可靠性信息和生产定型的质量控制信息共同构成了生产定型任务可靠度的先验信息, 要将生产定型阶段的质量控制信息作为先验信息合理引入, 首先应分析生产定型阶段质量控制措施调整及其对可靠性的影响。
生产定型的工艺调整是在设计定型生产工艺的基础上完善固化的, 由设计定型时的单件小批量加工方法变为生产定型时的多件批量加工方法。为确定生产过程质量控制对产品可靠性的影响,分别从“人、 机、 料、 法、 环” 等方面进行对比分析。
a) 加工工具和工艺方面
与设计定型相比, 加工方式由手工焊接改为设备自动焊接, 设计专用加工工装和专用测量工具替代原单件加工方法, 目的是为了提高生产效率和保证生产定型产品装备质量的一致性。
b) 生产人员和生产环境方面
从设计定型到生产定型生产单位保持不变,生产环境保持一致, 生产人员经过研制过程的生产经验积累, 生产技术趋于成熟稳定。
c) 生产材料方面
生产用原材料按原设计要求定点采购, 因国产化需求改变的十几种元器件通过可靠性增长试验进行测试, 质量有保证。
d) 质量管理和法规方面
生产定型的主要目的是固化工艺, 在设计定型的基础上, 进一步地补充完善工艺等质量管理规定, 管理体系更为成熟完善, 质量控制水平进一步地提升。
2 生产定型可靠性验证试验方案制定方法
2.1 试验方案制定思路
在明确了生产定型任务可靠度验证目的后,生产定型阶段的可靠性验证试验方案制定可以采用多种思路。
a) 依据相关国军标规定采用经典方案[1], 根据产品任务可靠度指标、 置信度等选取试验方案。一般在试验周期长, 且试验经费投入较大的情况下, 推荐选择该方法。 但考虑到产品生产定型周期和经费等因素的影响, 选择经典方法并没有充分体现出生产定型和设计定型之间的关联性和继承性, 没有利用设计定型阶段的试验信息和试验结论, 造成了一定的信息损失。
b) 利用设计定型阶段可靠性信息, 采用Bayes 方法确定生产定型阶段的任务可靠度验证试验方案。 该方法基于可靠性增长理论[2-3], 利用设计定型阶段任务可靠性信息, 在综合考虑生产阶段的各种工艺控制、 原材料与零部件选用等质量控制因素对产品可靠性影响的情况下, 确定生产定型阶段的产品可靠性先验分布, 以此为基础,制定产品生产定型阶段的可靠性验证试验方案。采用该方案, 在使用设计定型阶段的可靠性信息时, 必须充分地考虑生产过程质量控制对产品可靠性的影响。
2.2 先验信息结构分析
生产定型是在设计定型后, 通过产品生产工艺控制和材料选用等质量控制进一步提升产品的可靠性水平, 确保稳定生产出满足规定可靠性要求的产品。 在设计定型阶段, 产品开展了可靠性鉴定试验, 形成了任务可靠度的评估结论。 这些可靠性信息为生产定型积累了可靠性先验信息,合理利用这些先验信息可以合理地制定生产定型阶段的可靠性验证方案。 因此, 为了合理地利用先验信息制定试验方案, 应首先分析产品生产定型可靠性信息构成, 并明确它们之间的相互关系。
a) 设计定型阶段可靠性信息
设计定型阶段可靠性信息主要为可靠性鉴定试验信息。 在利用可靠性鉴定试验信息时, 可以直接以可靠性鉴定试验评估结论为基础, 以确定生产定型任务可靠度的先验分布, 从而避免了对可靠性鉴定试验信息的各种折算。 同时, 可靠性鉴定试验评估结论已被各方接受, 因此, 从可靠性鉴定试验评估结论入手可使得先验信息的利用更加客观可信。
b) 生产定型阶段质量控制信息
在生产过程中, 设计人员将针对产品生产过程中不断暴露出的工艺等缺陷, 采取有效的质量控制措施, 从而使产品可靠性不断地提高, 直到能稳定地生产出可靠性满足要求的产品。 因此,在生产稳定状态下, 生产定型可靠度与设计定型可靠度应相差不大, 其可靠性水平主要受生产过程中生产工艺、 材料选用、 生产设施、 人员的操作与管理水平、 质量控制水平的影响, 这些因素构成质量控制信息。 根据经验统计及文献资料[4],对于机电产品, 其设计缺陷, 元器件、 零部件缺陷和工艺缺陷大体上各占1/3 左右。
综上所述, 生产定型可靠性水平由设计定型可靠性和生产定型阶段的质量控制水平决定。 在设计已定型的情况下, 影响生产定型阶段可靠性的主要因素是质量控制因素。 由此可见, 设计定型阶段的可靠性信息和生产定型阶段的质量控制信息共同构成了生产定型阶段可靠性的先验信息,利用这些先验信息参与制定生产定型可靠性验证试验方案, 可以合理地确定生产定型试验量。
2.3 生产定型任务可靠度的先验分布确定
2.3.1 生产定型任务可靠度模型
为了充分地利用产品研制阶段的可靠性信息参与生产定型任务可靠度验证评估, 必须建立产品设计定型阶段与生产定型阶段的任务可靠度关系。 由上节分析可以看出, 产品生产定型状态工作可靠度是由其固有的工作可靠度与其生产质量控制因素共同决定的。 一方面, 为了生产出高质量的产品, 必须按照产品的各种设计规定, 对影响其质量的各种生产因素(如工艺流程, 原材料、零部件的选用, 以及生产管理等) 进行严格的控制, 确保生产出的产品满足设计规定。 而另一方面, 在产品实际的试生产过程中, 从提高生产效率, 提升质量控制水平出发, 对产品设计规定的工艺流程、 原材料与零部件选用, 以及生产控制管理程序等进行适当的调整与完善。
为了进一步地刻画产品生产定型任务可靠度与其固有(设计定型) 任务可靠度之间的关系,我们深入地分析产品工作期间的平均失败条次数。由于产品正常工作时间一般服从指数分布, 利用指数型产品的更新过程理论, 对于n 条产品, 当其固有的任务可靠度为R′时, 其实际工作过程中发生的平均失败条次数应为-nlnR′0。 与设计定型阶段相比, 在产品实际的生产阶段, 由于生产工艺固化过程中质量控制的调整与完善对任务可靠度的影响, 产品实际生产阶段的任务可靠度一般不高于其固有可靠度, 即对于n 条产品, 当其生产定型任务可靠度为R 时, 其实际工作过程中发生的平均失败条次数-nlnR 应大于或等于-nlnR′,多出的失败条次数n (lnR′-lnR) 实际上是由生产质量控制因素的影响造成的, 根据μ 定义有:

由此可以得出生产定型任务可靠度与设计定型固有任务可靠度之间有如下关系:

2.3.2 生产定型任务可靠度的先验分布
为了获得产品生产定型任务可靠度R 的后验分布, 需要首先研究设计定型任务可靠度的分布函数, 然后通过模型(2) 就可以得到产品生产定型任务可靠度的先验分布。 下面以产品任务可靠度为例, 给出其先验分布的确定过程, 对于不同任务阶段的可靠度的先验分布可以采用类似方法获得。
在产品设计定型阶段, 通过利用产品研制阶段的各种可靠性试验信息, 采用Bayes 综合评估方法给出了产品设计定型的任务可靠度验证评估结论[5-6]。 即在置信水平γ 下, 产品任务可靠度置信下限为R′Lq; 产品任务可靠度的点估计为。 利用上述验证评估结论, 就可以确定产品设计定型的任务可靠度的分布函数。 为了方便工程使用, 选用Beta 分布Beta (R′|a0, b0) 作为产品设计定型任务可靠度R′的分布函数, 其密度函数为:

其中, a0, b0为超参数, 可利用定型的可靠性结论获得, 即a0, b0可由下列方程组求得:

在获得产品设计定型任务可靠度R′的分布函数情况下, 就可以利用模型(2) 得到产品设计定型任务可靠度R 的先验分布。 对于给定的生产质量控制参数μ, 产品生产定型任务可靠度R 的先验分布为:

生产定型任务可靠度R 的先验分布(5) 在实际使用中并不方便。 为了工程应用方便, 使用Beta (R|a, b) 分布作为先验分布式(5) 的近似分布, 即产品生产定型任务可靠度R 的先验近似分布为Beta (R|a, b) 分布, 此时参数a, b 满足:
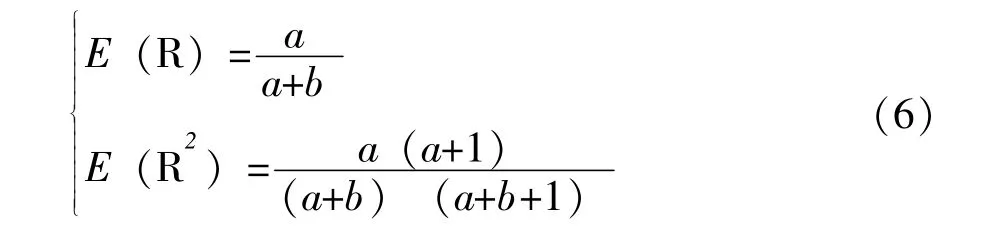
即:

其中μ, ν, 分别表示生产定型任务可靠度R的一阶矩和二阶矩, 即:

2.4 后验分布确定
对给定的生产定型任务可靠度Rq的先验分布Beta (Rq|a, b) 和任一生产定型试验结果(N, r),其后验密度函数为:

后验概率为:
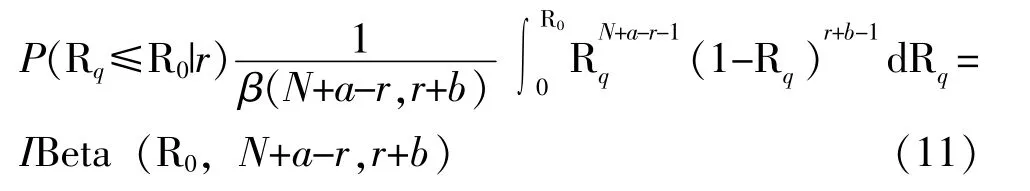
2.5 风险分析
对于生产方而言, 其风险为合格产品没有通过验证试验而被拒收的概率, 即P (没通过检验|Rq≥R0):
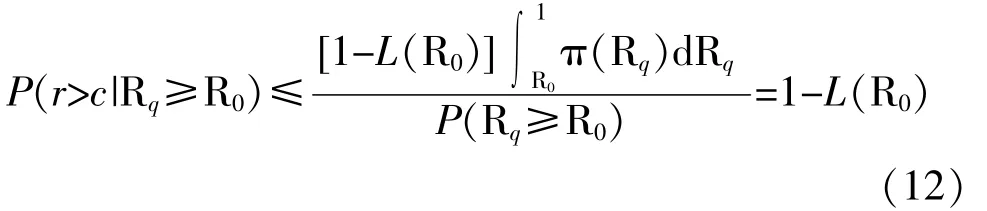
若给定生产方风险α, 则只需要求:

特别地:

对于使用方而言, 其风险为接收的产品为不合格产品的概率, 即P (Rq≤R1|通过检验):
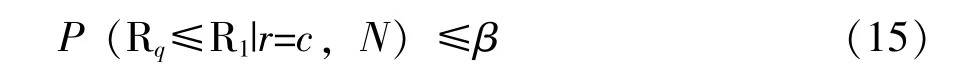
特别地:
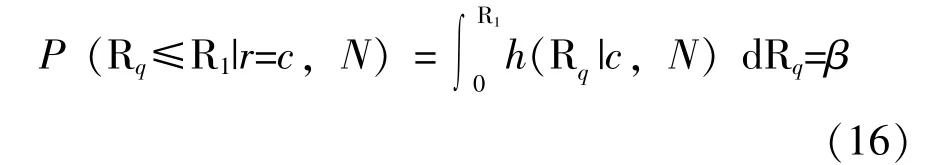
综上, 只需要求制定的验证试验方案(N, c)满足式(8) 和(9) 的联立方程组:即可满足生产与使用双方对风险的要求, 保证双方的利益。

3 某产品生产定型可靠度验证试验方案制定
假设设计定型试验阶段, 产品任务可靠度结论为: 在置信水平γq=0.7 下, 产品任务可靠度置信下限为R′Lq=0.853。 由于定型试验中, 既有产品数据, 又有分系统试验数据, 为方便起见, 可以利用MML 方法确定等效试验量[7], 由此确定b0=4; 进一步, 利用该置信下限可以得到参数a0的取值为:

由此, 在利用专家经验得到μ 和k 的取值后,即可利用式(11) 得到参数a 和b 的取值。 例如,在μ=0.09 时, 参数a 和b 的取值分别为:

因此, 即可在不同的试验方案下, 计算使用方风险。 经计算, 不同的μ 和k 取值下计算结果如表1 所示。

表1 产品任务可靠性验证试验方案列表
由表1 可以看出:
1) 在同一试验方案下, 随着比例系数μ 的增加, 使用方风险逐渐地增加;
2) 即使比例系数μ 取值较小, 在试验量很小时仍难以满足使用方的风险要求。
而根据GJBZ 20391[8]有关成败型产品验证规定, 0.85 任务可靠度的试验方案如表2 所示, 对比两个表中的数据发现, 采用Bayes 方法充分地考虑了设计定型试验数据, 可以采用较少的试验量来获得试验结果。
4 结束语
本文利用Bayes 方法研究了产品可靠性先验信息的转换问题, 建立了制造工艺对生产定型产品可靠性影响的统计模型和先验分布确定方法。 在此基础上, 提出了产品生产定型可靠性验证试验方案制定方法, 并进行了实例验证, 为水中兵器生产定型可靠性验证提供了方法指南和理论依据。

表2 试验方案

