预测水驱油田含水率的麦克斯韦模型及应用
雷宇田,邢 杨,周大霖,卢怡帆,刘 峰
(1.中国石油长庆油田分公司第十二采油厂,甘肃合水 745400;2.西安石油大学石油工程学院,陕西西安 710065)
随着我国注水开发油田逐渐进入中高含水期,准确预测含水率对水驱油田开发方案的制定,开发措施的调整具有重要意义。为此,国内外学者对含水率预测做了大量的研究和现场实际应用工作[1-3]。
自从20 世纪50 年代,苏联学者根据水驱油田开发规律,统计得到甲型、乙型、丙型和丁型4 种水驱曲线以来,水驱曲线在我国注水开发油田得到了广泛的应用[4]。截止目前,我国学者已研究出多种预测含水率的方法,主要有水驱特征曲线法和数学模型法。陈国飞等[5]根据预测生物生长的Von Bertalanffy 模型,建立了基于Von Bertalanffy 模型的含水率预测方法,可对水驱开发全过程进行预测,且不需考虑开发过程的影响;周鹏等[6]结合多参数的增产曲线,建立了新的随开发时间变化的含水率模型;朱圣举等[7]根据甲型水驱特征曲线和油田产量预测模型,提出了一种新的含水率预测模型,指出该模型的适用条件为油藏必须为稳定水驱;刘鹏等[8]将MMF 生长模型与水驱特征曲线相联合,建立了预测水驱油田含水率的联解模型,克服了水驱曲线和联解模型的不足,可对不同时间的含水率进行预测;张居增等[9]根据描述增长信息随时间变化的数学模型,建立了预测含水率的Usher 模型,并指出目前用于含水率预测的Logisitic 模型和Gompertz 模型均为Usher 模型的特例。以上水驱曲线法和水驱模型在水驱油田预测含水率中得到了广泛的应用,但存在模型参数多,模型计算过程复杂等特征。本研究基于概率统计中的麦克斯韦分布,建立了只含有1 个参数的含水率随开发时间变化的新预测模型,新模型可对不同类型,不同开发阶段的油藏进行预测,通过实例数据,与新模型计算结果进行对比,以验证新模型的可靠性和实用性。
1 模型的建立及参数求解
麦克斯韦分布的概率密度函数可表示为[10]:
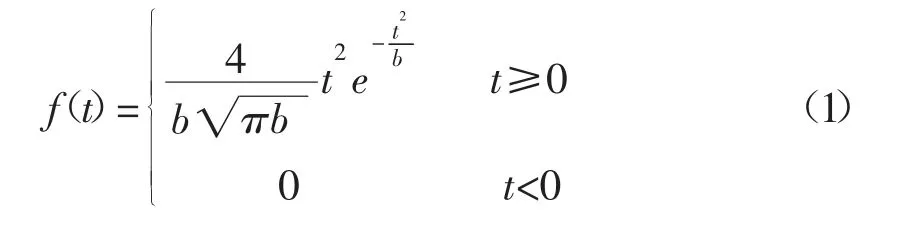
式中:t-油田开发时间,a;b-控制分布形态的常数。
由式(1)得:

油田从时间t 投入开发到∞的累积产油量为:

式中:NR-油田可采储量,t;Q(t)-第t 年的年产油量,t。
式(3)两端同除以NR,得:

由式(2)和式(4),得:

结合式(5)和式(1),得油田年产油量为:

式(6)两边对时间从0 到t 积分,可得油田累积产油量为:

当t=0 时,根据:
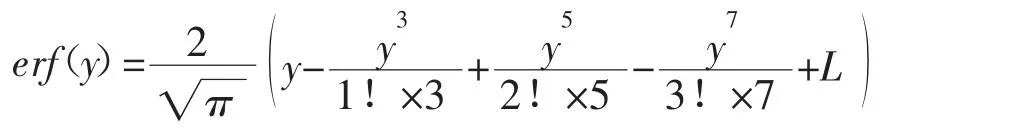
凡是能满足t=0,fw=0;t=∞,fw=fwmax=1 的模型,均可以用于含水率的预测。对于式(7),当t=0 时Np=0;t=∞时Np=NRmax、fw=fwmax,因此,式(7)可改写为:
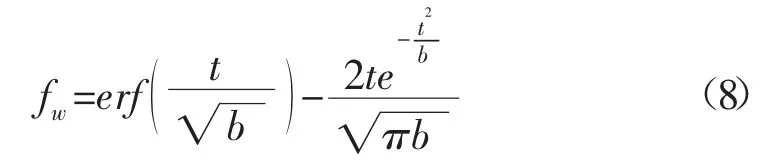
式中:fw-含水率,%。
式(8)即为新建的预测水驱油田含水率的麦克斯韦模型。从该模型中可以看出,模型中仅有一个未知参数b,根据油田实际含水率随时间的变化数据,应用一元多项式线性回归法,通过MATLAB 软件编程,当相关性最佳时,所计算出的b 即为所求得的值,该模型形式简单,且求解方便。
2 模型特征
当参数b 取不同的值时,新模型可以得到“一簇水驱曲线”,含水率随开发时间呈现出不同的上升规律,说明新模型能较好的描述不同类型油藏含水率随时间的变化关系(见图1)。曲线形状从“凹型”过渡到“S 型”再过渡到“凸型”,表明新含水率曲线呈现出多样性的特征,可以较好的预测含水率上升情况。对于存在无水采油期和较长时间低含水采油期的油田,新模型也能较好的进行描述。在实际应用中,当油田措施方案调整导致含水上升率发生变化时,可选取不同的参数值b进行预测,b 的取值范围为(0,+∞)。
3 实例应用
为了验证新模型对含水率的预测效果及实用性,以大庆油田南二三开发区葡Ⅰ组和平湖油气田M 油藏的实际开发数据为基础,应用式(8)对含水率进行预测,以验证新模型的可靠性。
3.1 大庆油田南二三开发区
大庆油田南二三开发区葡Ⅰ组1965-1987 年的实际开发数据(见表1、图2)[11]。将含水率和生产时间数据代入式(8),应用一元多项式线性回归法,通过MATLAB 编程计算,最佳拟合参数b=166.389 8,相关系数为0.987 2,得到大庆油田南二三开发区葡Ⅰ组新模型预测含水率的表达式为:

图1 不同参数b 取值下含水率与时间的关系
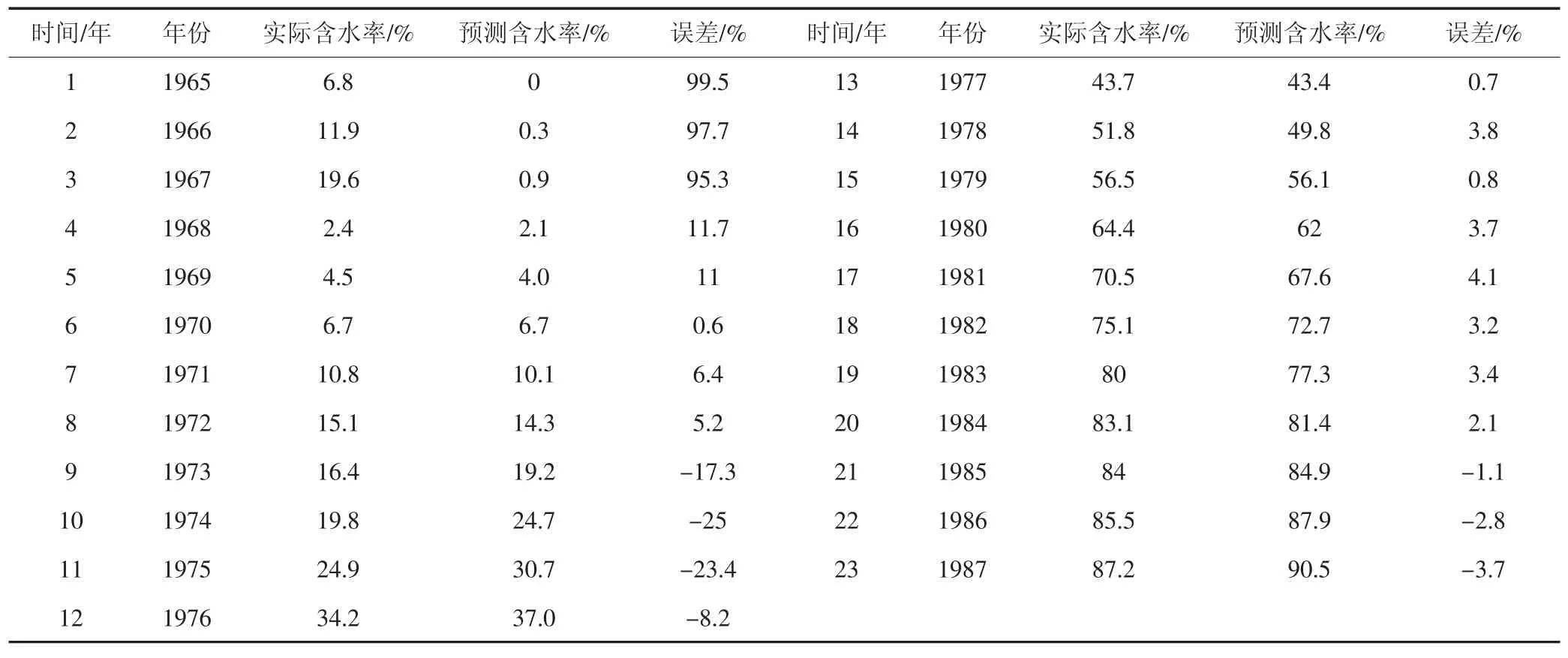
表1 大庆油田南二三开发区葡Ⅰ组含水率实际值与预测值对比

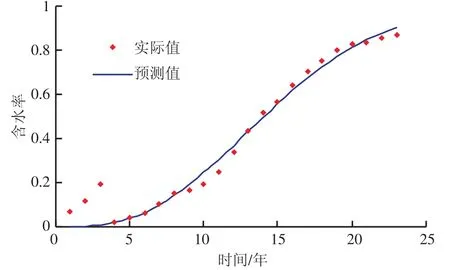
图2 大庆油田南二三开发区葡Ⅰ组实际含水率与预测含水率对比图
3.2 平湖油气田M 油藏
平湖油气田M 油藏1998-2010 年的实际开发数据(见表2、图3)[12]。将含水率和生产时间数据代入式(8),应用一元多项式线性回归法,通过MATLAB 编程计算,最佳拟合参数b=15.848 2,相关系数为0.991 7,得到平湖油气田M 油藏新模型预测含水率表达式为:
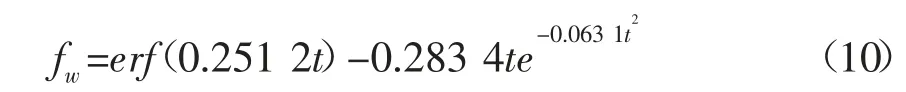
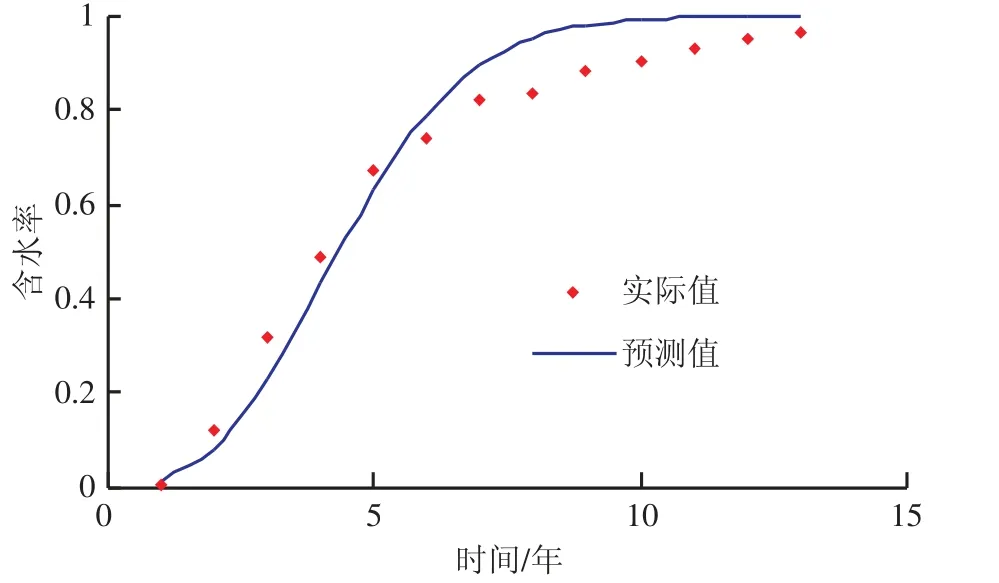
图3 平湖油气田M 油藏实际含水率与预测含水率对比图
3.3 大庆油田萨北过渡带区块
大庆油田萨北过渡带区块1969-1990 年的实际开发数据(见表3、图4)[13]。将含水率和生产时间数据代入式(8),应用一元多项式线性回归法,通过MATLAB编程计算,最佳拟合参数b=183.822 6,相关系数为0.993 5,得到大庆油田萨北过渡带区块新模型预测含水率的表达式为:
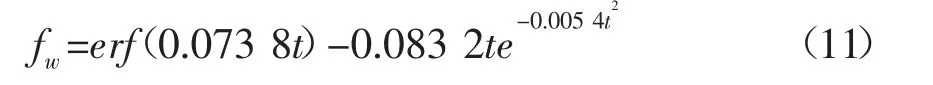

表2 平湖油气田M 油藏含水率实际值与预测值对比

表3 大庆油田萨北过渡带区块含水率实际值与预测值对比

图4 大庆油田萨北过渡带区块实际含水率与预测含水率对比图
从以上三个实例可以看出,随着水驱开发的进行,新模型预测含水率结果与实际含水率变化趋势相似(见图2~图4),预测精度较高,新模型预测以上三油田最后10 年绝对误差的平均值分别为2.88%、8.41%和7.29%。
4 结论
(1)将麦克斯韦模型用于水驱油田的含水率预测,与其他含水率预测模型不同的是,该模型中只有1 个参数,模型表达形式简单,参数计算方便,可为水驱开发油田生产动态分析和开发方案制定提供指导。
(2)通过选择不同的参数值b,可得到“一簇水驱曲线”,曲线形状从“凹型”过渡到“S 型”再过渡到“凸型”。当油藏类型不同,油田开发方案发生变化时,可灵活选取不同的参数值,对含水率随开发时间的上升进行预测。
(3)结合三个矿场应用实例证明了该模型的实用性和有效性,新型含水率预测模型趋势与实际趋势相近似,且预测数据与实际数据较接近,预测误差较小。
(4)所建模型反映了含水率随开发时间的变化,不需考虑开发过程的影响。但新模型是否适用于其他水驱开发油田,尚需更多油藏实例验证。

