基于IBAS-BP算法的冬小麦根系土壤含水率预测模型

许景辉 刘政光 周宇博

(西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100)

0 引言

淡水资源匮乏已成为全球性问题，在中国尤为严重。根据国家统计局的数据，我国每年农业用水总量约3 600亿m3，其中农业灌溉用水占比约90%，但农业水资源利用率只有40%～45%，水资源利用率较低[1]。监测作物根系所在位置的土壤含水率不仅可以提高灌溉用水利用率[2]，还能保证作物优质高产，对研究作物根系的水分也能起到积极作用[3]。农作物根系深度因土质不同而存在差异，但大多集中在0～60 cm浅土层。如冬小麦根深可达1.5～2.0 m，但90%的根量分布于0～60 cm表土层内[4]。通过表层少量传感器预测较深土层的含水率可有效减少设备投入、实现植株的精准灌溉，这对于改善灌水条件[5]、保护农业生态、实现智能灌溉具有重要意义。

近几年人工神经网络迅速发展，在解决函数逼近与数据预测等问题上效果良好。结合智能算法的优化改进型BP神经网络集合了优化算法在BP初始权值和阈值优化上的优势，具有良好的非线性映射能力，在不同行业中得到了广泛应用。在农业领域，李旭青等[6]将小波变换和BP神经网络结合，实现了土壤重金属含量反演，其效果良好，但步骤繁复。LIANG等[7]利用遗传算法(Genetic algorithm，GA)与BP神经网络结合，实现了土壤水分的反演，其效果良好，但GA迭代速度较慢。JIA等[8]尝试利用插值法与BP神经网络结合，在土壤金属污染的空间分布估算中获得较高的精度，证明了改进型BP网络的预测精度。在工业领域，张蓓等[9]利用PSO-BP算法对沥青混合料空隙率进行反演计算，大大提高了计算效率，但PSO算法易陷入局部最优的问题较为明显。谢劭峰等[10]用遗传算法优化BP-GA模型，实现了降水量预测，显示出BP-GA模型很好的非线性拟合能力，但算法较复杂，不易推广。王甜甜等[11]利用天牛须搜索(Beetle antennae search，BAS)算法优化BP神经网络，用BAS-BP模型进行风暴潮灾害预测，结果表明，该模型收敛速度快，具有较好的鲁棒性和较高的准确度。文献[12-13]利用BAS-BP模型对深孔加工中钻削力进行预测，其训练时间短，结果准确。以上研究表明，智能算法优化的BP神经网络具有良好适应性和较高的预测精度。

在这些智能算法中，天牛须搜索算法(BAS算法)具有较高的准确性。该算法基于天牛采食原理，适用于多目标函数优化，无需知道函数具体形式及梯度信息便可实现自动寻优[14]，且寻优速度较快[15-16]。但由于天牛初值的随机性，该算法在解决高维函数方面不够突出,容易陷入局部最优[17]。为提高BAS-BP模型的预测精度，本文对传统BAS算法进行改进，提出IBAS-BP算法，将算法中单个天牛改进为天牛群，最大程度地弱化“天牛”随机初值与方向对算法造成的影响，从而避免算法陷入局部最优，提高BAS算法寻优的准确性，采用PSO-BP、GA-BP和BAS-BP模型与IBAS-BP模型进行对比，探究IBAS-BP模型在冬小麦根系土壤含水率精确预测方面的能力。

1 材料与方法

1.1 IBAS-BP预测模型

1.1.1IBAS-BP搜索算法

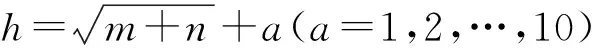
由于BAS算法随机初值与方向的随机性易造成算法陷入局部最优，为进一步提高BAS算法的寻优准确性，提出IBAS(Improved beetle antennae search)优化算法。利用改进天牛群搜索算法对BP神经网络进行优化，可提高BP神经网络的预测精度[19]。具体步骤为：

(1)构建k维随机向量表述种群中每个天牛须的朝向，作归一化处理，计算式为

(1)

式中 rand(·)——随机函数

b——天牛须朝向

BP神经网络模型中，若输入层神经元个数为M(本文中为11)，输出层个数为L(本文为1), 隐含层神经元个数为N，此时模型搜索维度k=MN+NL+N+1。

(2)单只天牛左右须空间坐标为

(2)

式中xir——第i只天牛右须在第t次迭代后所在空间位置

xil——第i只天牛左须在第t次迭代后所在空间位置

dit——此天牛的左右须间距

xt——此天牛所在位置的质心坐标[20]

(3)确定左右须气味强度

根据适应度函数fitness可确定左右须的气味强度，从而迭代更新左右天牛须所在位置

(3)

式中δit——第i只天牛在第t次迭代时所对应的步长因子

sing(·)——符号确定函数

tsim(j)——第j个样本的输出值

yj——第j个样本的实际值

(4)确定步长因子

采用步长因子控制每只天牛的天牛须搜索范围，为避免搜索区域过小和局部极小值出现，应设置较大初始步长[21]。而为保障搜索的精细化，采用线性递减权值来设置步长,计算式为

δit+1=δite(t=0,1,…,n)

(4)

式中e为步长衰减系数，应取[0,1]之间靠近1的数字，但目前为止，步长因子数值设置尚未有完整理论体系指导，本文选用0.95。同时，通过多次实验，确定初始步长δ=3，迭代次数n=100。

由文献[21]可知，天牛须算法相较于传统的PSO、GA等搜索算法，可通过衰减因子与步长设置，加快迭代，在迭代速度上有着明显的优势[21]，而其收敛速度也远超过传统PSO、GA算法。但其固有缺点在于天牛所在初始位置值的随机性，而通过取代单个天牛，可有效避免这一缺点。

1.1.2最优解生成

对天牛群中的每只天牛所在位置进行初始化，其中每个天牛所在初始位置都应取[-0.5,0.5]之间随机数，并将其保存在bestA集中。同时根据适应度函数，记录此时所有天牛的全局最佳适应度，记录在bestfinessA集中。之后，根据式(2)对每只天牛所在位置进行迭代更新。每一次更新完成，都应根据式(3)迭代左右须位置，求取对应的适应度函数值[22-23]。及时更新bestA集与bestfitnessA集。最后，通过比较两个集合中整个天牛群的全局最佳适应度，得出整个天牛种群的最佳初始位置bestB和种群最佳适应度bestfitnessB，即为最优解。

不断重复上述过程，当适应度函数值达到设定值(本文取0.001)或迭代进行到最大次数(本文设定为100)，可将此时bestB中的解集认为是训练所得最佳解，即BP神经网络的最优初始权值和阈值,之后进行二次训练学习。具体流程如图2所示。

1.2 实验数据

实验于西北农林科技大学教育部旱区农业水土工程重点实验室的灌溉试验站(108°24′E，34°18′N，海拔521 m)进行。选用所测的713组实验数据，每组包含风速(m/s)、风向、气温(℃)、相对湿度(%)、露点温度(℃)、大气压力(Pa)、太阳辐射(W/m2)、20 cm土层含水率(%)、30 cm土层含水率(%)、20 cm土壤温度(℃)、30 cm土壤温度(℃)共计11个信息。其中，冬小麦根系大多分布在浅层土壤[24-25]，选用Acclima-TDR-315型时域反射仪，埋入深度50 cm土壤进行实测，作为预测数值对比数值。选定其中所测606组数据作为训练集，107组作为测试集。设置IBAS算法中e为0.95，δ为3。BP神经网络训练次数设为100，训练目标0.001，学习速率0.001。

1.3 模型精度评价

为合理评价改进IBAS-BP模型对于冬小麦根系所在土壤含水率的预测精度，以相对误差和决定系数为评估标准。其中相对误差越小，则样本拟合效果越好。决定系数在[0,1]内进行变动，数值越接近于1，表明模型预测精度越高，效果越好，而数值越小，越接近0，则说明模型预测效果越差。

2 结果与分析

2.1 IBAS-BP模型验证

根据所测数据，构建基于IBAS-BP神经网络、BAS-BP神经网络、GA-BP模型[26-27]、PSO-BP模型[28]的4种预测模型，分别简称为IBAS模型、BAS模型、GA模型和PSO模型。各模型对于冬小麦根系深度50 cm含水率的预测结果如图3所示。并根据相对误差和决定系数对IBAS-BP模型预测精度做出评估。

由图3a可以看出，粒子群优化算法与BP神经网络组成的PSO模型的预测值与实际土壤含水率测定值基本吻合，但在含水率小于15.8%和大于16.4%处，模型预测误差过大。测试集中，PSO模型的相对误差为0.006 9，决定系数R2为0.673 2,表现差于BAS模型，可能与输入输出相关关系的回归曲面精度不够高有关。由图3b可知，GA模型具有良好的收敛性[21]，但整体拟合效果不佳，预测值集中在16.1% ～ 16.2%，与实际结果存在偏差。且当土壤含水率小于15.7%时，会出现较大误差。在测试集中，模型的相对误差为0.005 7,R2为0.767 7。且遗传算法步骤复杂，运算繁多。由图3c可知，BAS模型的预测值和实测值基本吻合，但在含水率大于16.4%和小于15.8%的范围出现误差。计算可知，BAS模型的相对误差为0.004 7，决定系数R2为0.805 9，具有良好的精度和适应性，但实验效果对于初始天牛所在位置依赖过重。由图3d可知，IBAS模型几乎与实测数据全部吻合，误差更小，极为接近于实测数据。且在测试集中，相对误差仅为0.004 5，而决定系数R2为0.840 7，体现了优化算法的良好适应性与优越性。4种模型的评估结果如表1所示。

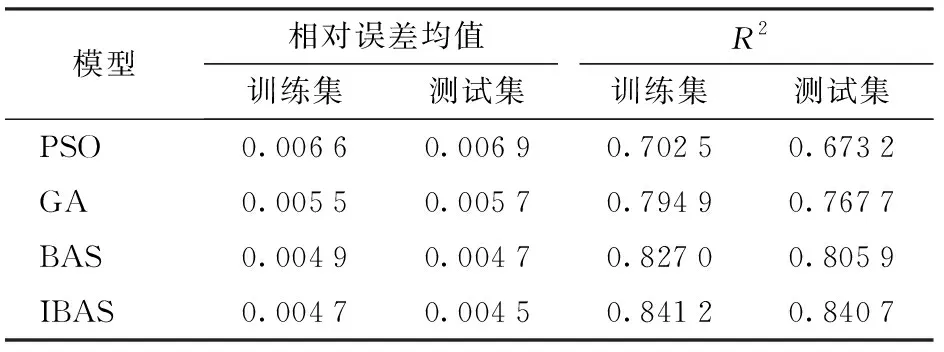
表1 不同模型效果对比Tab.1 Comparison of effects of different models

2.2 模型优化

ZHENG等[21]提出，在BAS算法中，可通过调整步长保证BAS算法的渐近收敛概率为1。据此可知，IBAS算法的迭代速度和迭代耗时应与式(4)中的δ和e的参数设置有关。为进一步提高IBAS-BP算法的估测精度，实现对冬小麦根系所在50 cm处土壤含水率的精准预测，本文对以上参数进行调整。其中e选用0.55～0.99的等差数列，而δ则选用2～8的等差数列。验证可知，当e<0.85时，迭代速度并不会受较大影响，而当e>0.95时，迭代速度会下降，迭代次数增多，在此区段内，取0.95时，效果最佳。同理，当δ<4时，迭代速度加快，而取3时，IBAS算法收敛性最好，速度最快，迭代次数最少。

研究结果表明，IBAS-BP算法能通过大量数据训练，消除自然条件下的综合影响因素，提高对于冬小麦浅层根系的土壤含水率预测精度。而通过调整单个天牛步长δ以及衰减系数e,与土壤含水率的预测精度提升存在较好的相关性，改进后，其训练集和测试集的建模回归决定系数R2最高分别可达0.841 2和0.840 7。相对误差也最接近于1，体现了卓越的预测精度和良好的适应性。这为实现冬小麦土壤含水率的快速检测提供了理论基础。同时，通过对比4种算法在不同的含水率预测结果分析，得出IBAS-BP神经网络建立的预测模型最优，其模型决定系数R2大于0.8。BAS模型相对IBAS模型较差，但仍优于PSO模型和GA模型，GA模型相对前3种模型表现最差。

3 结论

(1)利用IBAS搜索算法优化后的BP神经网络预测模型，其预测精度明显提高，优化后的BP神经网络初始权值和阈值明显优于随机状态下的权值和阈值，克服了BP神经网络收敛速度慢、易陷入局部极小值等缺点。

(2)在IBAS-BP模型中，调整步长和衰减因子等参数可以提高冬小麦根系含水率的迭代速度。在不同应用数据集中，可通过参数调整来进一步提高模型的适应性。

(3)建立的IBAS-BP预测模型可对50 cm深度冬小麦根系土壤含水率实现准确预测，这对于进一步提高水资源利用率、节约农业用水具有参考价值，可为保护灌溉资源、实现农业灌溉系统的自动化和智能化提供借鉴。