180 nm CMOS微处理器辐照效应敏感外设及其损伤剂量的概率模型分析

刘一宁 杨亚鹏 陈法国 张建岗 郭 荣 梁润成

（中国辐射防护研究院 太原030006）

目前国内许多单位开始研发耐辐射机器人，或进行相关实验研究［1-6］，为了合理估计机器人内复杂电路在辐射环境下的可靠度，需要了解包括微处理器在内各器件在工作状态下受到辐照损伤时对辐照效应最敏感的功能，并建立失效剂量的统计概率模型。由于在线辐照实验的复杂性，目前国内对商用微处理器在线辐照损伤的研究较少。

本文以60Co 作为辐射源，对一定样本量的特征工艺尺寸为180 nm 的互补金属氧化物半导体（Complementary Metal Oxide Semiconductor，CMOS）微处理器进行了总剂量实验，测量了器件的辐射效应。找出了片内对总剂量效应敏感的外设，分析其原因并建立了电离辐照实验数据统计处理方法和检验方法，给出了微处理器片内闪存存储器（On-chip Flash memory，FLASH）由于总剂量效应导致写入失效的概率模型。对比了三参数威布尔分布、两参数威布尔分布、正态分布和对数正态分布的模型参数和K-S检验结果。

1 实验方法与原理

1.1 实验样品及辐照条件

开展了180 nm CMOS 微处理器芯片的60Co 在线电离辐照实验，实验样品为4片Cortex-M3内核的增强型32 位微处理器―STM32F103C8T6，辐照时器件工作在运行状态，设计了相应的最小系统电路板、周围器件屏蔽体和上位机软件，实现闪存存储器、定时器、通用同步异步收发串口、片内模拟数字转换器、直接存储器访问、通用输入输出等功能的实时在线测试。

辐照实验在中国辐射防护研究院的60Co γ 放射源上进行，放射源活度为666 TBq，使用丙氨酸剂量计 测 得 芯 片 处 剂 量 率 为95.13 Gy（Si）·h-1和97.3 Gy（Si）·h-1，总 照 射 剂 量 为1 523 Gy 和1 489 Gy（水）。

1.2 测试方案

搭建了由被测电路、通讯电路、剂量计、屏蔽体和上位机组成的在线总剂量效应实验环境，如图1所示。在线实验过程中，将被测芯片搭载于被测电路上置于辐照室内，并将丙氨酸剂量计紧贴被测芯片固定以测量其受照剂量；将通讯电路置于铅砖搭建的屏蔽体内，以排除其辐照故障的影响。实验时被测芯片按照预设程序进入工作状态，上位机监控串口信号，并判断被测芯片工作状态是否正常。

微处理器在工作状态下通过片内模拟数字转换器和直接存储器访问功能获取电源的电压值，并用定时器判断FLASH读写功能，将上述结果通过通用同步异步收发串口输出到通用输入输出引脚发送给上位机，从而同时实现对上述外设的在线功能检验。

图1 在线辐照损伤实验系统示意图Fig.1 Schematic diagram of on-line-irradiation-effect-test system

2 实验结果

2.1 辐照损伤剂量

不同于对微处理器进行移位测试，在线辐照损伤实验需要在器件连续正常工作情况下实时测量器件各外设的功能，因此每次同时测量的芯片数量有限。

本次实验使用了两个剂量计，测得总照射剂量分别为1 523 Gy和1 489 Gy（水），1、2号被测芯片所用剂量计的结果换算为95.13 Gy（Si）·h-1，3、4 号被测芯片所用剂量计的结果换算为97.30 Gy（Si）·h-1。它们的其他功能在FLASH 写入功能失效前均没有失效，因此将FLASH写入失效剂量作为微处理器芯片总剂量效应的最敏感参数，结果如表1所示。

表1 被测芯片在线辐照测试的FLASH写入失效剂量Table 1 Failure dose of FLASH write during test

2.2 辐照损伤分析

本实验中，FLASH 写入最先失效，而直至测试结束FLASH 读取都未失效，其不同之处在于FLASH写入过程需要高压，因此推断是产生高压的电荷泵器件最先损坏。

其原理为：产生高压的电荷泵器件一方面工作电压较高，所以内部晶体管的氧化层需要更厚，更容易产生氧化物陷阱电荷；另一方面强电场下电子-空穴对复合减少，导致同等剂量下其陷阱电荷累积更为严重［7］。最后，独立的FLASH存储器的辐照实验也表明电荷泵输出电压会因辐照下降［8］。

而在180 nm的技术节点下，由于微处理器使用的金属氧化物半导体场效应管栅氧化层变薄，沟道内电子可以通过隧穿效应与栅氧化层内由于辐照产生的被俘获空穴进行复合［9］，因而芯片内其他外设的结构本身具有较高的耐辐射能力。因此，电荷泵器件相对其他部分更易遭受辐射损伤。

3 概率模型的建立与检验

3.1 概率模型的建立方法

建立FLASH失效剂量的概率模型，需要先假设这些数据符合某几种已知的分布，并估计出相应的分布参数，然后检验实验数据与这些分布的符合程度，选择符合最好的概率模型。本文中的概率模型使用MATLAB实现，处理过程分为如下几个步骤：

首先推断实验数据可能符合的几种概率模型，总剂量实验中常见的分布模型包括：

正态分布，其累积概率分布函数如下，其中μ和σ是x的平均值和标准差：

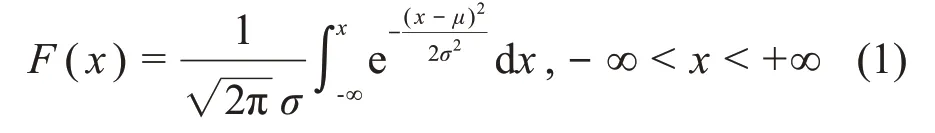
对数正态分布，其累积概率分布函数如下，其中m 和σ 并不是x 的平均值和标准差，而是lnx 的平均值和标准方差：

两参数威布尔分布，其累积概率分布函数如下，其中η是尺度参数，β是形状参数：

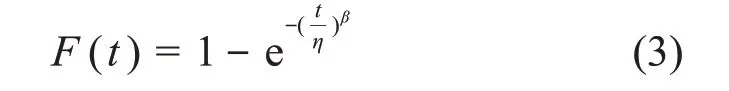
除此以外，三参数威布尔分布在本研究中也纳入考虑，其累积概率分布函数如下，其中γ 是位置参数。

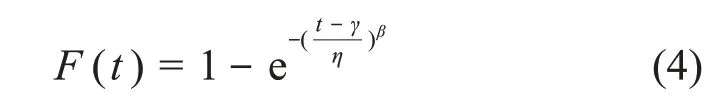
本为使用了一种三参数威布尔分布的简便参数估计方法，首先将其累积概率分布函数变形为线性方程，通过求解相关系数极值的方法估计其位置参数，通过换元将其转换为二参数威布尔分布，再通过极大似然方法估计其尺度参数和形状参数。

将式（4）取2次对数后可得：

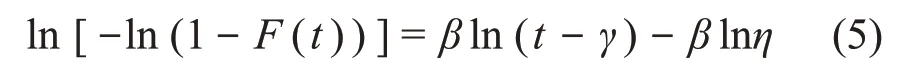
这时，令y = ln[-ln(1- F(t))]，x = ln(t - γ)，将式（5）转化为线性方程，其中不可靠性F(ti)用中位秩作为最佳估计［10］：

极大似然估计的方法就是令似然函数的导数为0，解似然方程组获得其参数的估计值。二参数威布尔分布的似然函数为：

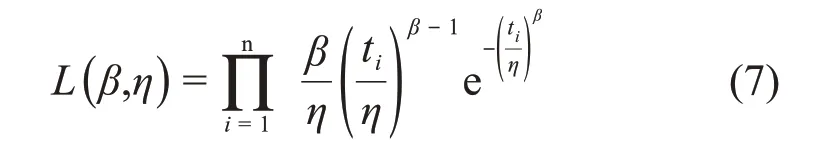
正态分布的似然函数为：

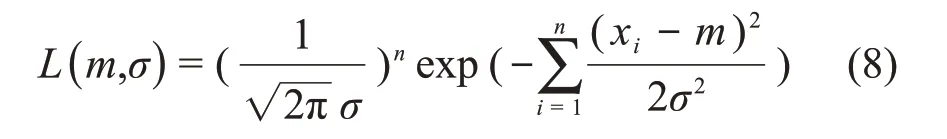
其次，检验方法为K-S法，其主要思想是将假设的概率分布函数与经验分布函数相比较。设样本容量为n，由小至大排序的样本为x1≤x2≤x3…≤xn，则其经验分布函数为：

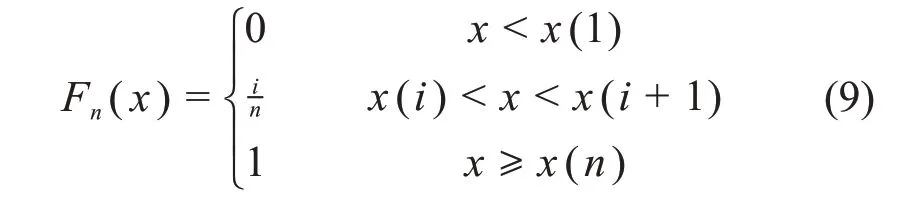
其检验统计量为：

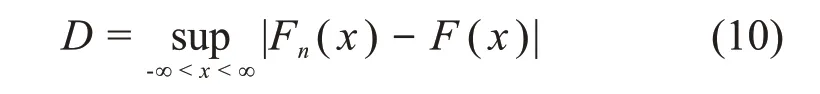
将检验统计量D与临界值CV（Critical Value）对比，小于临界值时认为假设成立，多个假设都成立时，检验统计量D 越接近临界值CV 的假设越不可靠。

3.2 失效剂量的4种概率模型对比

本文定义的FLASH 失效剂量是指第一次检测到器件写入失效的时间，该失效剂量是表征芯片抗辐照能力的重要参数。

使用前述方法对4 种概率模型分别估计其参数，结果如表2所示。

表中参数含义如§3.1 所述。其中，三参数威布尔分布的η是尺度参数，在形状参数一定的情况下，尺度参数越大，密度函数图像越扁平；β 是形状参数，是威布尔分布中最重要的参数，当β＞1时，密度函数图像有1 个峰，这个峰随着β 的增大而变高变窄；γ是位置参数，该参数表示图像的整体平移。

表2 4种概率模型的参数Table 2 Parameters of the four probabilistic models

使用上述参数绘制这4种概率模型的累积概率分布函数及用中位秩估计的累积失效实验点，如图2 所示，纵坐标F（D）表示累积到横坐标相应剂量D时器件失效的概率。

发现这4个模型的累积概率分布函数在中等累积失效概率附近比较接近，三参数威布尔分布在低累积失效概率阶段更加陡峭。

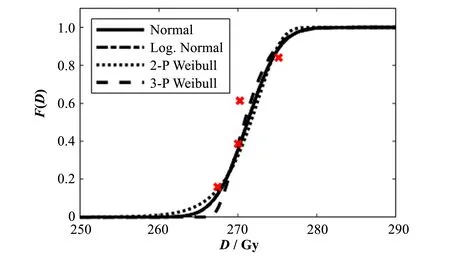
图2 4种概率模型的累积分布函数Fig.2 Cumulative distribution function of the four probabilistic models

使用上述参数绘制这4种概率模型的概率密度曲线如图3所示，纵坐标P（D）表示在横坐标相应剂量D处器件失效的概率。

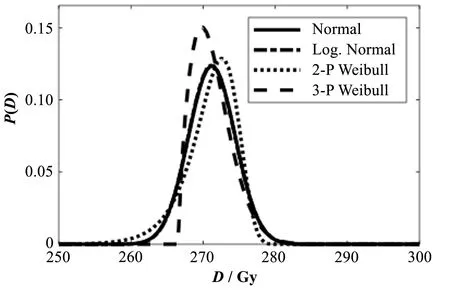
图3 4种概率模型的概率密度函数Fig.3 Probability density function of the four probabilistic models

三参数威布尔分布呈现正偏态，且左侧明显更加陡峭；而二参数威布尔分布呈现负偏态，且右侧更加陡峭；正态分布和对数正态分布比较接近。

用K-S法分别检验这4种模型，检验统计量越小表示与模型符合得越好，结果如表3所示。

表3 4种概率模型的K-S检验Table 3 K-S test of the four probabilistic models

三参数威布尔分布具有最低的检验统计量，且其各参数描述微处理器辐照损伤时具有明确的意义，适合作为描述片内闪存存储器的总剂量效应导致写入失效的概率模型。

首先，由于总剂量辐照损伤描述的是射线在硅氧化物中沉积的总剂量导致的损伤，在剂量积累到阈值之前，辐照产生的陷阱电荷导致的电荷泵输出电压降低对存储器的影响在其忍受范围内，其功能就没有变化。在本实验中其位置参数为266.03，这表示在本实验条件下，266.03 Gy为引起存储器写入失效的剂量阈值。而其他三种分布缺少表述这一物理过程的参数。

然后，当辐照在硅氧化物中累积的电荷突破阈值后继续增加时，电荷泵失效导致存储器写入失效的概率也就越来越高。在本实验中其形状参数为1.758 4，而形状参数大于1 的威布尔分布就用于表述器件失效概率随横坐标递增而增长的情形。而且一般认为形状参数小于3.6 的威布尔分布是正偏态的，即数据中位数小于均值。所以根据本文三参数威布尔分布概率模型的参数估计结果，180 nm CMOS 微处理器多数器件的耐辐射剂量应小于均值，评估使用该微处理器的电学系统耐辐射能力时应予以考虑。

最后，在本实验中三参数威布尔分布的尺度参数为5.274 6，该参数表示本实验中各芯片的片内闪存存储器失效剂量结果的离散程度较低。

对已发表的同型号芯片在中等剂量率63.3 Gy（Si）·h-1下的实验数据［11］进行同样的处理，实验数据如表4所示，结果如表5所示。

表4 中等剂量率下的FLASH写入失效剂量Table 4 Failure dose of FLASH write during medium dose rate test

表5 中等剂量率下概率模型的参数Table 5 Parameters of the four probabilistic models during medium dose rate test

发现在中等剂量率下，其形状参数为2.900 7，也在1～3.6之间，表示其失效概率在超过阈值后也随剂量的递增而增长，且概率密度函数也为正偏态。其尺度参数为43.726 1，表示该实验失效剂量结果的离散程度较高。其位置参数为196.47，表示在该实验条件下196.47 Gy 为引起存储器写入失效的剂量阈值，低于较高剂量率下的结果。

用K-S 法分别检验上述4 种模型，结果如表6所示。

表6 中等剂量率下的K-S检验Table 6 K-S test of the four probabilistic models during medium dose rate test

发现在中等剂量率下，虽然4 种概率模型的差别减小了，但是三参数威布尔分布仍然是描述微处理器辐照损伤较好的概率模型。

4 结语

本文对特征工艺尺寸为180 nm 的CMOS 微处理器进行了在线辐照实验，找出了片内对总剂量效应敏感的功能为FLASH的写入功能，并推断其原因是电荷泵器件的辐照损伤。

本文还建立了微处理器在线辐照实验数据的统计处理方法和检验方法，使用三参数威布尔分布概率模型，描述了63.3～97.3 Gy（Si）·h-1剂量率下使用60Co 源辐照时，180 nm CMOS 微处理器片内FLASH由于总剂量效应导致的辐照损伤，并分析了各参数的物理意义，可用于评估使用该微处理器电学系统的辐射性能。