高分子/棒状纳米粒子复合物的分子动力学模拟

刘爱清，徐文生，徐晓雷，陈继忠，3，安立佳，3

（1.吉林大学化学学院,长春130012；2.中国科学院长春应用化学研究所,高分子物理与化学国家重点实验室,长春130022；3.中国科学技术大学应用化学与工程学院,合肥230026）

聚合物纳米复合材料（PNC）是指将纳米粒子（球、柱、盘形）分散在高分子基体中而形成的新型功能材料，在近几十年来引起了学术界和工业界的广泛关注.研究发现，不同大小、形状和功能的纳米粒子对材料的力学、光学、电学、热学和流变性质有显著的影响［1～7］，除了这些性能的改善，聚合物纳米复合材料还在生物医学［8，9］、液体传感［10，11］、燃料电池［12，13］、包装［14，15］及靶向药物输送［16］等领域有广阔的应用前景.纳米粒子对于材料性能的改变多样且不易调控，基于对聚合物纳米复合新材料的开发需求，理解纳米粒子对于高分子基体的结构、动力学和流变性质的影响尤为重要［17］.

科研人员采用实验［18～22］、模拟［23～31］和理论［25～27，32，33］研究了纳米粒子对高分子流体的力学、电学及流变性质等的影响.通常，加入的纳米粒子分为对称性（金纳米粒子和富勒烯）和非对称性（棒、管、碟及多面体等）.实际上，通常认为高度非对称纳米粒子（如层状硅酸盐、碳纳米管和棒状纳米粒子）在改变高分子基体的性质方面比球形（或近球形）纳米粒子更具潜力.研究表明，非球形纳米粒子如碳纳米管（CNT）、纳米棒（NRs）［20］和纳米线（NWs）极大地提高了所合成复合材料的机械强度［34，35］、电导率［36，37］、热导率［38］和光学性能［39］.此外，纳米棒/纳米管填充聚合物的研究取得了重要的应用，如高导电性碳纳米管［40］和金属纳米线复合材料［41］、光学活性金纳米棒复合材料［41］和集光半导体纳米棒复合材料［36］等.棒状纳米粒子最受关注的特点之一是，在比传统球形纳米粒子浓度低得多的情况下，可以使材料的特性增强（如力学强度、阻燃性和电导率）.Balazs等［42］模拟了将球状和棒状纳米粒子加入高分子中，研究发现，当含量相同时，与球形纳米粒子相比，棒状纳米粒子提供了更好的力学性质.Starr等［43］研究了非平衡态下纳米粒子形状对材料的剪切黏度和拉伸强度的影响，发现类棒状纳米粒子对体系黏度的增加更大，而片状纳米粒子更大程度提高了材料的拉伸强度.

此外，棒状纳米粒子通常作为探针，为探究体系的微流变学提供了独特的方法，通过追踪其运动轨迹来探测材料的纳米尺度动力学和结构［44，45］.Clarke等［46］研究了纳米复合材料中纳米棒扩散和高分子动力学，发现细纳米棒在高分子溶液中扩散得更快，而在缠结熔体中扩散达到一个平台，并发现纳米棒减慢了非缠结高分子链的运动.另外，Composto等［17］探究了纳米棒在体系中的的运动状态对高分子链扩散的影响.Composto等［47］也对聚合物在纳米复合材料中的扩散进行了研究.他们发现球形和短各向异性纳米粒子均使聚合物扩散系数随纳米粒子浓度的增加而单调下降.然而，聚合物扩散在低纳米粒子浓度时减慢，在长各向异性纳米粒子网络形成的临界浓度以上时恢复.

无论是作为改变基体性能的掺杂剂还是作为探测体系性质的探针，纳米粒子的引入对高分子基体的结构、动力学及流变性质的影响亟待阐明.基于此，本文构建了非缠结柔性高分子链加入不同体积分数纳米棒的高分子纳米粒子复合物模型.采用非平衡态分子动力学模拟研究了剪切场中不同体积分数的纳米棒对高分子链的结构、动力学和流变性质的影响.

1 模型和方法

在所研究的模型体系中，柔性高分子链和棒状纳米粒子均采用Kremer-Grest模型［48］.柔性高分子链内和链间的排除体积相互作用为纯排斥的Lennard-Jones势能：

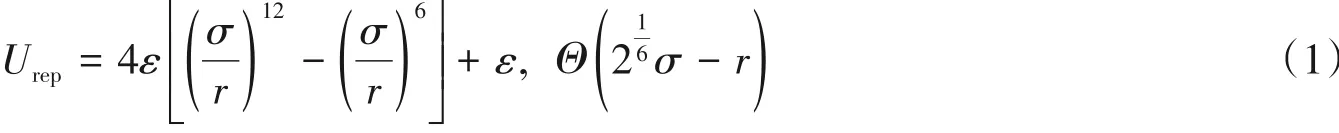
链内相邻粒子间的键势能为有限拉伸（FENE）势能［48］：

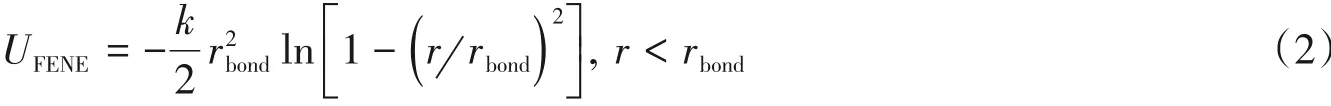
采用经典参数弹性系数为k=30εσ2，最大键长为rbond=1.5σ，保证了链不能互相穿越.对于棒状纳米粒子的排除体积相互作用及链内相邻粒子间键势能与柔性高分子链相同.纳米棒具有另外的一种键角势能，通过控制键角势能参数（K）来控制其刚性，势能函数如下：

式中：θ0=180°，K=800.

高分子链与纳米棒粒子间的排除体积相互作用为Lennard-Jones势能：

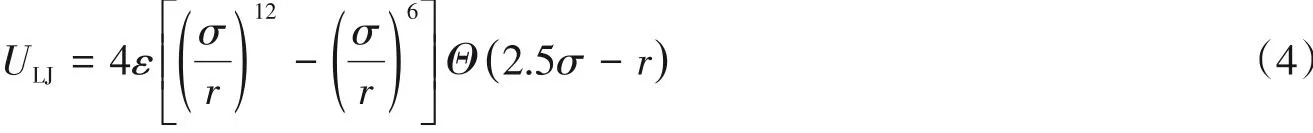
式中：r=|ri-rj|，ri和rj分别为空间中两粒子i和j的坐标；Θ(x)为赫维赛德函数；当x＜0，Θ(x)=0时，x≥0，Θ(x)=1.其中柔性链与纳米棒粒子之间的吸引使纳米棒分散均匀.

本文模拟了纯熔体和不同体积分数纳米复合物的平衡态和稳态剪切场的性质，所有的物理量都用标准的Lennard-Jones势能约化单位表达，即质量m，能量尺度ε，空间尺度σ，时间温度T=εkB，这里kB为玻尔兹曼常数，kB=m=σ=ε=1.0.模拟盒子为立方体，盒长均大于链长以避免尺寸效应.模拟时间步长为0.01，采用NVT系综，耗散粒子动力学（DPD）热浴保证体系恒温，Lees-Edwards边界条件用来产生流场，这里x为流场方向，y为涡度方向，z为梯度方向，因此剪切速率可以表示为γ˙=∂vx∂z，计算了一系列剪切速率（0.00008～0.05），所有模拟均采用了Lammps软件.

本文模拟了高分子熔体和不同体积分数φ（0.8%，1%，5%，10%）的高分子纳米复合物体系体积分数指纳米棒包含的粒子数与体系中总粒子数的比值.每条柔性链长Lc为30σ，棒长Lr为10σ.详细的模拟体系参数列于表1.

Table 1 Length of cubic box size(L),the numbers of flexible polymers(Nc),the numbers of nanorod polymers(Nr)and percentages(φ)of nanorods referred to different systems

2 结果与讨论

2.1 平衡态性质

纳米棒加入到高分子熔体中得到了多种浓度的复合物，纳米棒均匀分布在体系中［图1（A）］.在平衡态下，讨论了高分子链的均方回转半径与均方末端距的尺寸变化，并与纯熔体的相关值时进行比较［图1（B）和（C）］.研究表明，纳米粒子对高分子基体尺寸的影响是复杂的，与纳米粒子的类型、尺寸和分散状态有关［49～56］.Mackay等［50］通过聚苯乙烯/聚苯乙烯纳米粒子的中子散射实验发现，聚苯乙烯链发生了扩张且随着纳米粒子浓度的增加而增加，而聚苯乙烯/二氧化硅纳米粒子［49，51］的实验表明聚苯乙烯链的尺寸没有受到影响.对于各向异性纳米粒子，实验发现，将10%（质量分数）的单壁碳纳米管分散在聚苯乙烯基体中，聚苯乙烯链尺寸增加近36%［56］.本文模拟结果表明，纳米棒的体积分数为10%时仅增加约3%，说明纳米棒对高分子链的统计平均尺寸影响很弱.

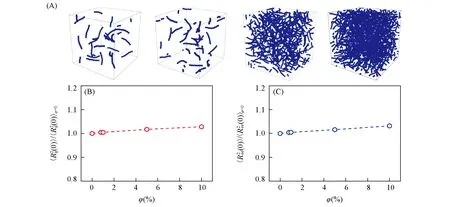
Fig.1 Structural properties of polymers in nanocomposites with different nanorod volume fractions at equilibrium

本文也观测了纳米棒对高分子链运动的影响，探究了高分子链质心的扩散系数（D）和松弛时间（τ）.扩散系数由高分子链质心（rcm）的均方位移（MSD）求得：

对于球形纳米粒子，模拟表明高分子链的扩散系数随着纳米粒子的增加而减小［31，57］.而对于各向异性纳米粒子，高分子链穿过各向异性障碍物运动时，构象熵减小，从而导致自身扩散变慢［58～60］.另外，研究发现，增加纳米棒的体积分数，更多的高分子链段会存在于纳米粒子表面形成的界面层［61］，高分子链的扩散系数减小.图2（A）示出了模拟体系中高分子链的扩散系数与体积分数的关系.表明高分子链的扩散系数随着纳米棒含量的增加而降低，当纳米棒的体积分数为10%时，高分子链的扩散系数降低约54%，强烈地阻碍了高分子链运动.另外，高分子链的松弛时间（τ）由下式计算：

式中：R(t)是t时刻高分子链末端矢量.高分子链的松弛时间随着纳米棒含量的增加而增大，当纳米棒体积分数为10%时，松弛时间相应地增加了约53%［图2（B）］.上述关于结构和动力学行为的讨论表明，纳米棒的加入基本不会影响高分子链的尺寸，而对高分子链的运动影响严重.

2.2 剪切场下的链结构性质

式中：Δri表示粒子i与链质心之间的距离，α，β是笛卡尔坐标.Gαα是高分子链在α方向上的均方回转半径张量.Gαβ的3个特征值能够表征高分子链的形状，即定义张量对角化后3个轴向方向的尺度.其中，最大特征值G1，最小特征值G3和中间特征值G2的加和为均方回转半径高分子链在平衡态下统计平均形状为球形，即为零剪切下的高分子链的均方回转半径.体系施加的剪切强度可以由无量纲物理量是剪切速率，τ为链最长松弛时间）来表征.一般来说，剪切场下的高分子链的行为由特征值分为2个区，在弱剪切区（Wi＜1），高分子链基本不发生形变；在强剪切区（Wi＞1），高分子链会沿着流场方向拉伸和取向.图3示出了加入不同体积分数纳米棒，归一化的链均方回转半径和回转张量与Wi的关系.Wi＜1时，曲线维持一个平台值，高分子链不受流场的影响，并未拉伸；当Wi＞1时，随着流场强度的增加，所有体系中的高分子链的持续增加，同时也发生变化，即随Wi的增加增大，而相应地减小.说明高分子链在流场方向拉伸，梯度和涡度方向压缩.由图3可以看出，剪切场下纯熔体（φ=0）中的高分子链的结构符合剪切场下的一般行为，而加入纳米棒的高分子链的结构曲线与纯熔体基本一致，表明在相同剪切强度（Wi）下，纳米棒对流场中高分子链的构象变化无本质影响.

除上述结构物理量外，高分子链形状变化的另一特征是回转张量的特征值之比，即和其中G1＞G2＞G3.当高分子链的形状为标准球形时，G1=G2=G3.图4模拟结果显示，对于所有体系的高分子链来说，当Wi＜1时高分子链形状基本保持不变.Wi＞1时则高分子链沿主轴拉伸，剪切越强，越趋近扁平状.因此，在相同的剪切强度下，纳米棒不会影响高分子链的形状变化.

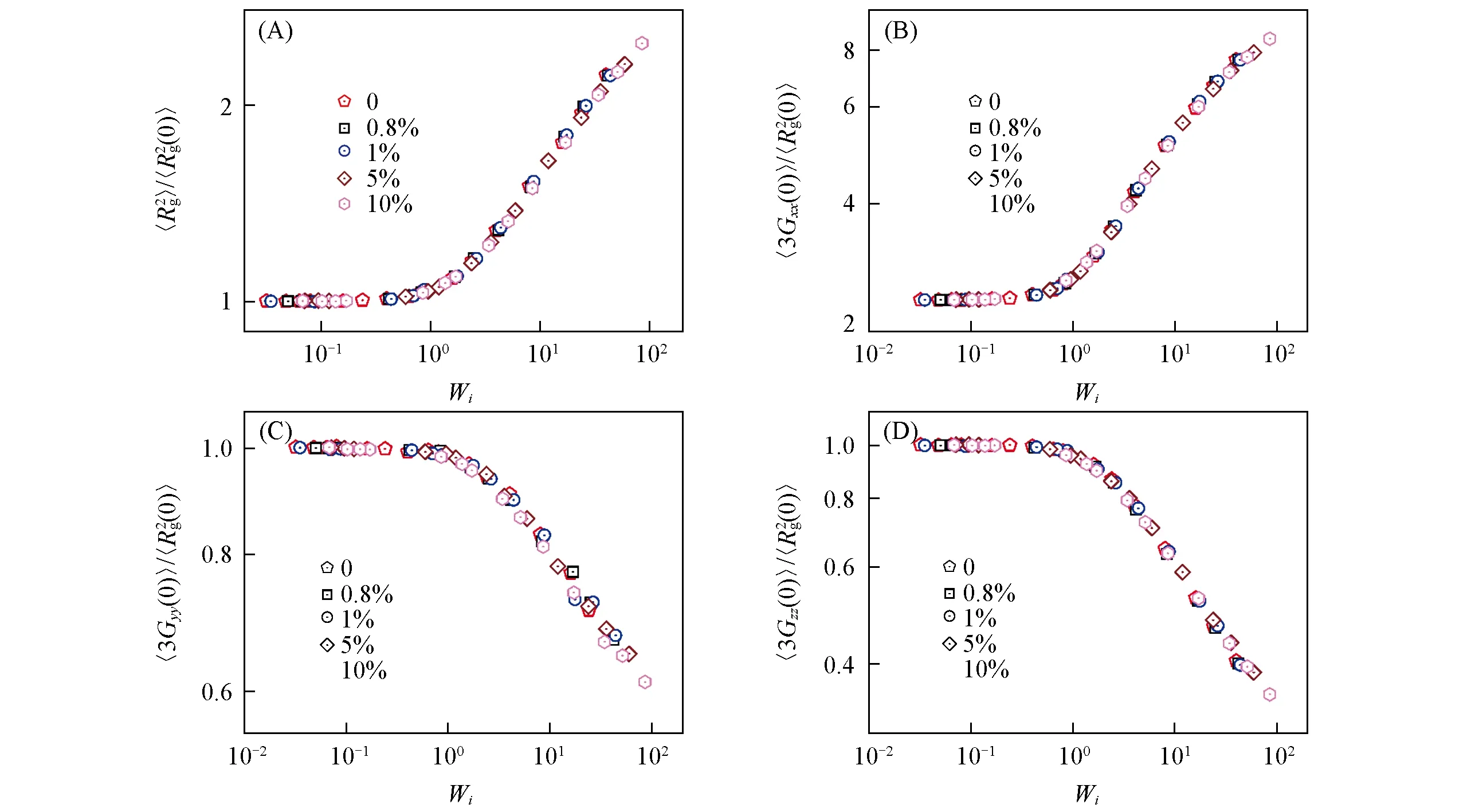
Fig.3 Mean-square radius of gyration and gyration tensor normalized by the radius of gyration under zero-shear as a function of Wi for different volume fractions nanocomposites

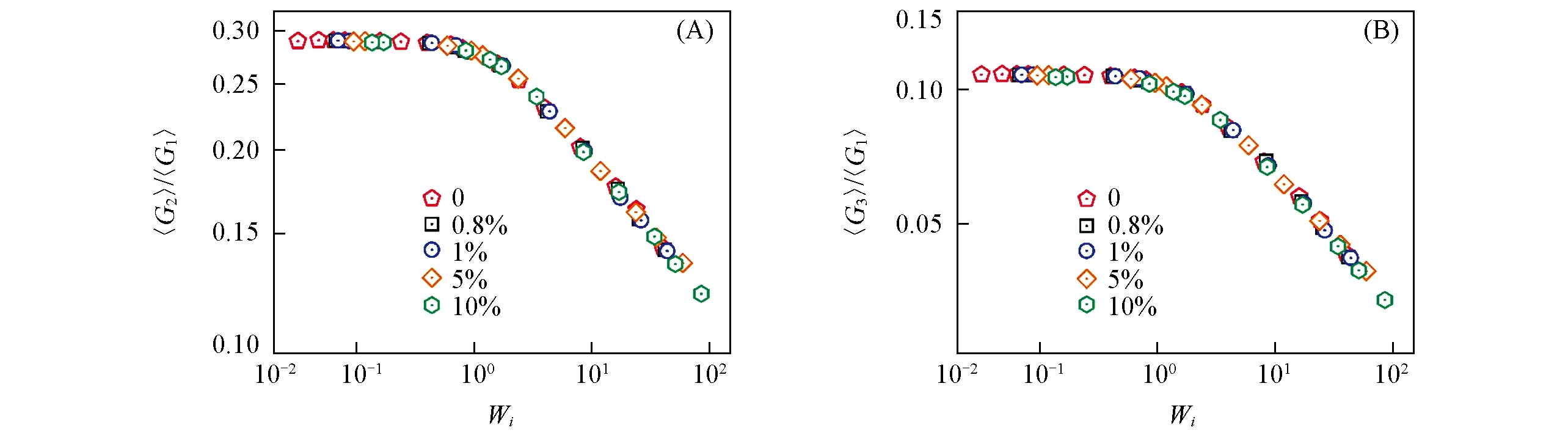
Fig.4 Ratio of the medium(G2)and largest(G1)eigenvalues(A)and ratio of the smallest(G3)and largest(G1)eigenvalues(B)of the gyration tensor as a function of Wi

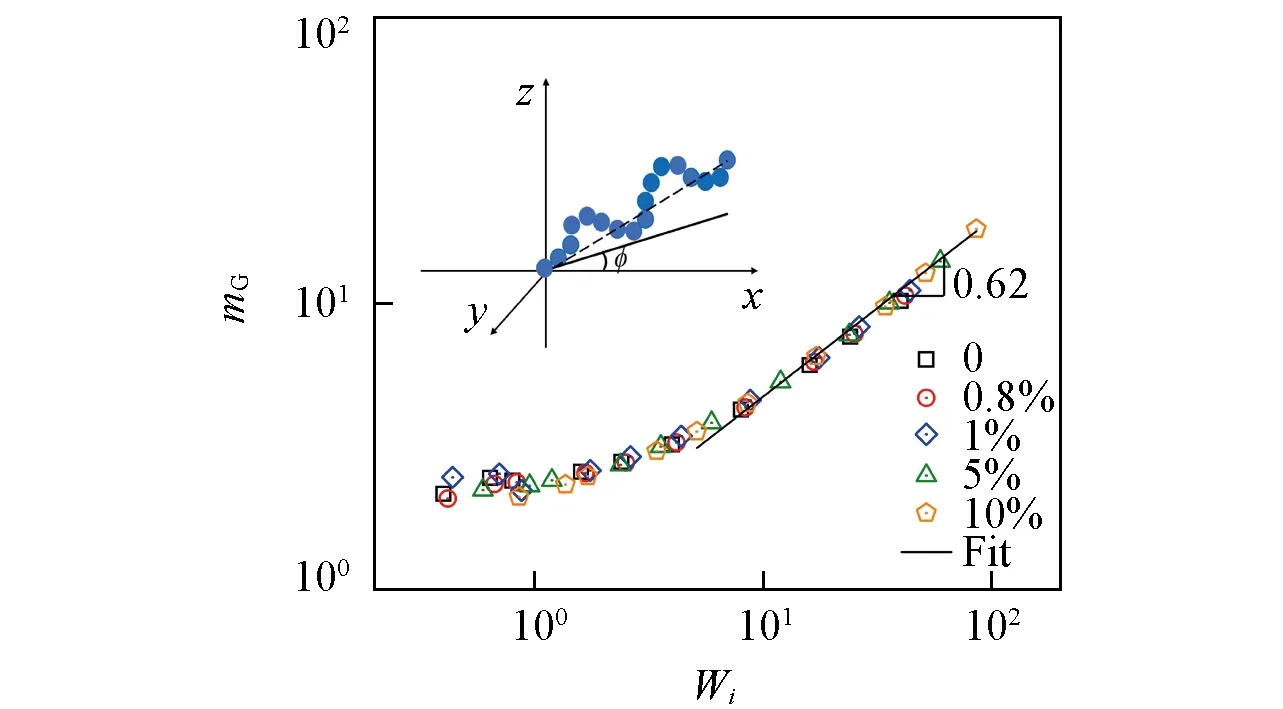
Fig.5 Orientation resistance parameter mG as a function of Wi for different volume fractions

剪切场下高分子链除了会发生拉伸形变外，还会发生链取向.高分子链的取向性质可以用取向抑制参数mG来表征，其由以下式表示［62～64］：

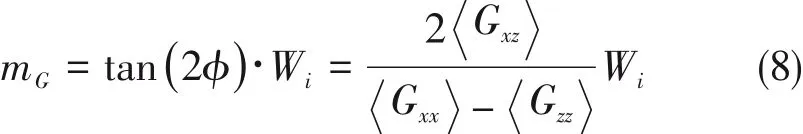
式中：φ为链的特征向量在剪切-梯度平面上的投影与流场方向的夹角.图5示出了不同体系中的高分子链平均取向mG与Wi的模拟结果.高分子链在平衡态中是无序状态，而流场会导致其沿着流场方向取向.在剪切场中，对于小Wi，高分子链的mG与Wi无关［63］.图5的模拟结果显示，处于小剪切时，mG保持一个稳定值，φ减小，链沿着流场方向取向（图5插图）；在强流场区，随着剪切强度的增加，mG明显增大，拟合Wi＞3的区间发现所有曲线符合同一标度关系这与剪切场下高分子溶液的结果一致［62］.曲线的一致性说明了相同剪切强度下，纳米棒的加入不会影响高分子链的平均取向.

2.3 剪切场下的链Tumbling运动

高分子链在剪切场中不停地运动，由于分子链不同部分所处位置不同，在梯度方向的速度差使得分子链转动，同时伴随着自身形变.称为Tumbling运动.为了得到这种运动的特征时间，通常计算高分子链构象改变的交叉关联函数（Cxz）.其计算公式如下［65～68］：

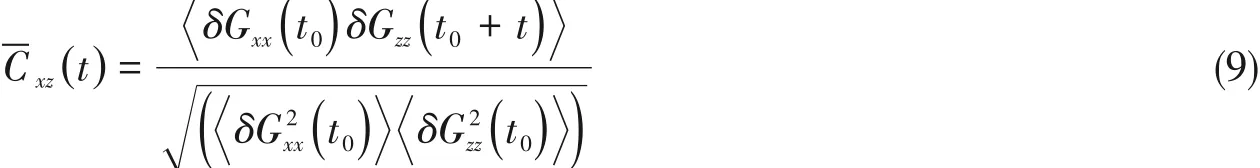
式中：δGαα=Gαα-Gαα.图6（A）示出了几种体系中Wi=20的交叉关联函数曲线.在这些曲线中，在t=0的两侧都存在1个波峰和波谷，类似正弦曲线，说明高分子链沿流场方向拉伸及沿梯度方向收缩的耦合运动［69］，峰高差值表示链的形变振幅.波峰和波谷之间的时间差是Tumbling运动的半周期.运动速度可以用频率ftb表示，可以通过计算.在相同的剪切强度（Wi=20）下，随着纳米棒的增加，曲线峰宽增大，而且峰高差值随着体积分数的增加而减小，表明高分子链的形变减弱.由图6（A）计算得到运动频率（ftb），图6（B）示出了在不同剪切强度下，不同体积分数的纳米复合物中高分子链的运动频率.随着Wi的增大（Wi＞1），所有体系中的高分子链Tumbling运动加快，这与纯高分子体系的模拟与实验结果类似［65，70］.在纳米复合物中，高分子链可能更多的是进行拉伸回缩运动，纳米棒的存在使高分子链很难进行翻滚运动，而且我们推测纳米棒体积分数的增大使得它们之间的相互关联作用增强，高分子链受到的束缚使其在有限空间内更难进行拉伸回缩运动.因此，加入纳米棒后，高分子链的运动频率减小，且与纳米棒的体积分数成反比，从而高分子的运动频率对剪切强度的依赖性依次减弱.

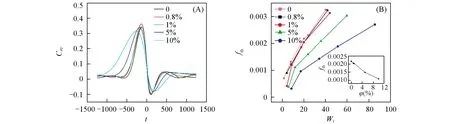
Fig.6 Cross-autocorrelation function Cxz against simulation time t with Wi of 20(A)and frequency of tumbling motion(ftb)as a function of Wi(B)for various volume fractions

2.4 剪切黏度

图7 示出了本文模拟的不同体系的η-Wi曲线.体系黏度符合线型链的一般规律，Wi=1是黏度曲线出现明显的剪切变稀区的临界剪切强度.当Wi＜1，由剪切黏度曲线外推可近似得到体系的零切黏度（η0)，结果列于表2中.与纯熔体相比，纳米复合物体系的零切黏度较大，且随着纳米棒体积分数的增加而增大；当Wi＞1时，体系发生了剪切变稀且所有曲线遵循相同的幂指数η-W-ni(n≈0.39).由图7插图可见，剪切强度Wi=20时，体系的剪切黏度随着纳米棒的增多而单调升高，因此，纳米棒定量地改变了体系的剪切黏度，而剪切变稀行为对流场的依赖性几乎不变.

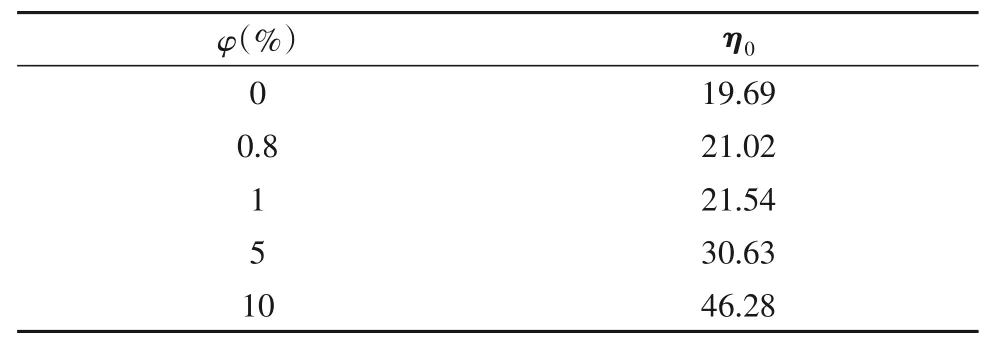
Table 2 Zero-shear viscosities(η0)of different nanocomposites and pure melt

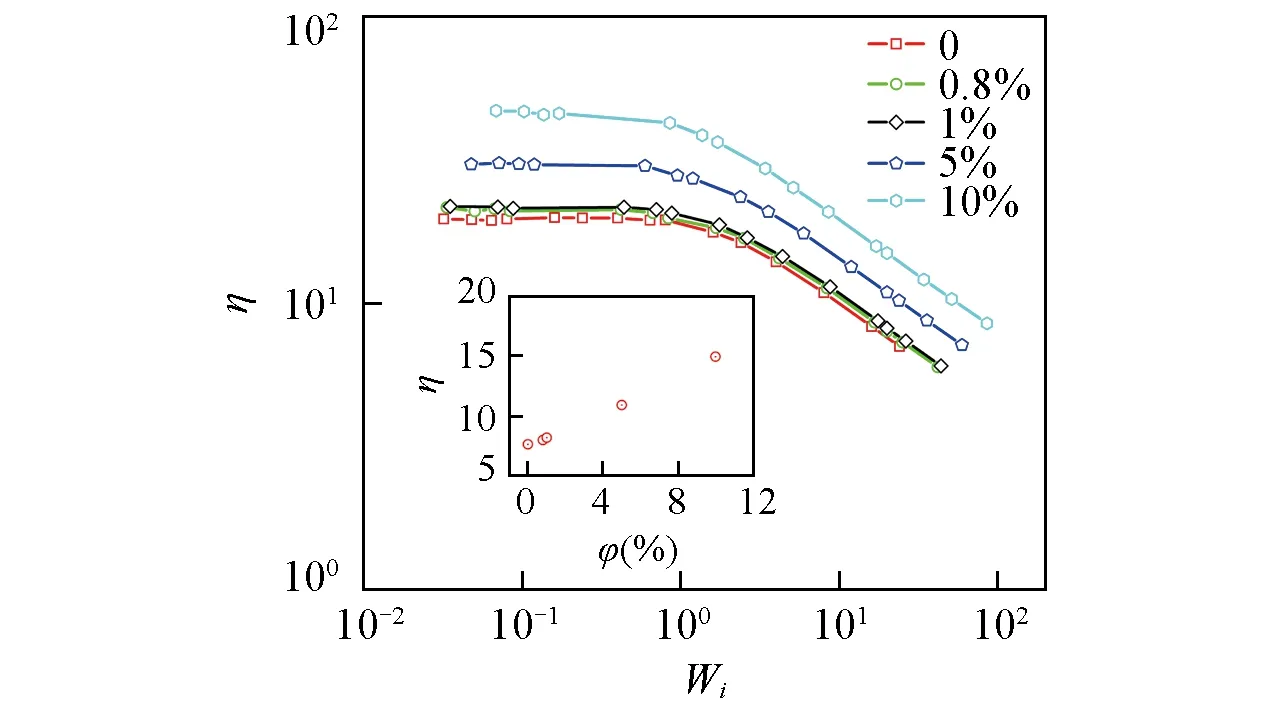
Fig.7 Shear viscosity(η)as a function of Wi for different volume fractions

3 结 论

本文主要讨论了剪切场下加入不同体积分数的纳米棒对高分子基体的影响.在平衡态时，纳米棒对高分子链的尺寸几乎没有影响，但严重阻碍其运动.在剪切场下，在相同Wi下，复合体系中高分子链的尺寸、形状和取向度与纳米棒的体积分数无关，然而高分子链的动力学性质受到抑制.复合体系的剪切黏度曲线展现了与纯高分子熔体基本一致的行为：小剪切强度下黏度为平台值，大剪切强度下出现剪切变稀.随着纳米棒的增加，体系的剪切黏度相应地增大.另外，本文研究了加入相同体积分数的纳米棒，对比发现长纳米棒使高分子链扩散变慢，剪切黏度增加，而对其结构性质影响很弱.研究成果有望为纳米复合材料的改性以及结构-性能关系的阐述提供一定的指导意义.