基于冗余任务消减的边缘应用性能优化

宋 煜，张 帅，严永辉，钱柱中

（1.江苏方天电力技术有限公司，南京 211102；2.南京大学计算机软件新技术国家重点实验室，南京 210023；3.南京大学软件新技术与产业化协同创新中心，南京 210023）

0 概述

虚拟现实（Virtual Reality，VR）和增强现实（Augmented Reality，AR）技术能够帮助用户在各类应用中获得更好的体验，如医生利用VR 技术可以重复地模拟手术以寻找最佳手术方案，消费者借助AR技术可以在商场中实时查看各类产品信息。VR 任务中对用户视野的3D 实时渲染以及AR 任务中对真实场景的实时识别均为计算密集型任务，由于用户终端计算性能有限，因此需要在远程云服务器上完成此类任务。然而，移动终端和远程云服务器之间带宽有限且网络不稳定，当终端发起与远程云服务器之间的大量实时数据传输时，网络延时会对应用效果造成较大影响。

在5G 时代，移动基站可以作为边缘云计算节点取代远程云服务器的部分功能。相较于远程云服务器，边缘云计算节点到用户终端物理距离更近。一方面，边缘云计算节点到用户终端具有更高的传输速度；另一方面，由于物理距离近，因此可以对某些特定场景下的应用做更细致的优化。例如，同一个VR 场景中的多个用户所需要渲染的视野图像都来自同一个虚拟世界建模，为这几个用户渲染的图像往往存在冗余，文献［1］针对此类冗余进行了优化，显著提升了VR 应用的实时响应性能。

在一些AR 应用中同样也存在着类似的冗余。以AR 导航为例，在一个边缘云计算节点附近的AR导航用户往往具有非常相似的周边环境，那么在AR识别过程中，多个导航用户对环境的识别任务就会存在冗余。因此，如何利用这样的冗余来减少边缘云节点的计算量，提升整体的用户体验，成为一个有待研究的问题。

本文介绍基于缓存的AR 性能优化方法，包括任务请求处理、边缘节点组织和缓存管理等方面的优化。在此基础上，对可部署资源有限场景下优化用户时延的问题进行数学建模，进而针对中小规模和大规模场景分别提出IDM 和LDM 算法，并通过实验验证算法性能。

1 相关工作

本节介绍计算卸载、移动AR/VR 应用、服务缓存放置和边缘计算资源管理等方面的相关工作。

在计算卸载方面，学者针对卸载内容、卸载时机、卸载方法等进行了大量研究［2-4］。WANG 等人将边缘节点网络抽象成一个图结构，研究对于给定的基站集合如何放置单独的边缘节点，从而使一个节点服务于多个基站，以尽可能地均衡负载并降低访问时延［5］。本文将边缘节点网络抽象成一个自组织并定时同步的网络，关注当多个用户都卸载到同一个边缘云网络时可能存在冗余计算的问题。在此基础上，研究在原基站添加边缘节点功能的部署问题，在总部署代价有限的情况下，通过安排新增边缘节点的计算资源量以降低用户时延。

笔者着眼于边缘计算背景下移动AR 应用的性能优化。在此之前，也有类似基于云计算的研究工作［6］，例如：Glimpse 通过缓存机制提升了识别准确率，使用触发帧选择的方法降低了无线传输时延［7］；面向指纹识别设计的VisualPrint 系统方案仅上传图像中最不同的特征，从而在低带宽的情况下对AR 任务进行卸载［8］。类似于AR，VR 也是边缘计算的杀手级应用，在此方面，LI 等人设计了MUVR 系统，在多用户的边缘云上对3D 渲染的冗余任务进行优化，提升了应用性能［1］。本文根据AR 和边缘计算节点的共同点做了进一步的优化：AR 的环境识别与请求发出的位置密切相关，而被分配到的边缘计算节点往往也与请求发出的位置距离不远，因此，针对这样特定的环境，本文使用缓存来进行计算冗余消减，从而有效减少传输和计算开销。

当多个服务器在处理相似的内容时，使用缓存就可以避免不必要的重复处理。关于如何放置服务缓存的问题，之前的一些工作调研内容包括视频缓存到服务器的最优分配方案、减少数据传输量的最优缓存位置、在稠密蜂窝网络中的动态服务缓存等［9-11］。本文研究在基站具有边缘计算能力的场景下如何部署计算缓存的边缘服务器和分配有限的资源，从而使用户获得时延更低的使用体验。

在边缘云中，资源管理对于服务质量和系统效率有着重要作用。目前，学者主要对资源分配和任务调度进行研究，包括均衡网络节点负载以优化应用性能、动态适应环境变化、基于层次架构的启发式负载分配算法、最小化总的加权服务响应时间的在线任务分配与调度算法等［12-14］。考虑到直接为基站增加边缘计算功能可以避免单独部署边缘节点的较大开销，本文研究在可部署代价有限的情况下如何分配可部署的计算资源，从而使用户时延降到最低。

因为移动增强现实（Mobile AR，MAR）是在现实世界情境下应用的，所以快速准确的物体识别成为能够将虚拟世界与真实世界互相融合的关键环节［15］。现有物体识别方法包括传统方法［16-18］和基于深度卷积神经网络的方法［19-20］。训练深度卷积神经网络是目前较为流行的方法，但是要达到一定的精度需要不小的计算代价。Chameleon 系统通过多节点协作，在计算资源投入和物体识别精度上取得了很好的权衡［19］。Focus系统通过使用简单的卷积神经网络构建近似索引，加快了对数据集的吸收和查询［20］。本文关注AR 识别请求与其物理位置之间的关系，以缓存的方式对物体识别进行加速。

2 问题描述

本节介绍基于缓存的冗余消减系统模型，对用户请求时延、用户轨迹预处理和节点部署做形式化表述，将问题聚焦于已知用户请求轨迹且部署总代价有限的情况下，如何为基站部署边缘节点的计算资源，以取得最低的平均时延，并证明此问题是NP-Complete 的。

2.1 基于缓存的冗余消减

2.1.1 节点缓存

本文考虑在一个城市中多个部署边缘计算功能的基站协作进行AR 识别的场景。当一个移动终端需要发起任务请求时，它会寻找距离自己最近的基站并将任务相关数据传送出去。基站收到这样的请求后，首先会检查相关数据是否已经被计算过。如果自己计算过，则直接返回计算结果；如果在其他节点计算过，则将请求重定向到缓存所在节点，由缓存所在节点返回计算结果；如果没有计算过，则在当前节点进行计算并把结果缓存在当前节点中，并通知所有其他节点。

为避免冗余计算，本文设置缓存为全局式的，即在整个城市中任意一个位置的请求都只会被计算一次。一次典型的基于缓存的AR 任务执行过程如图1 所示。

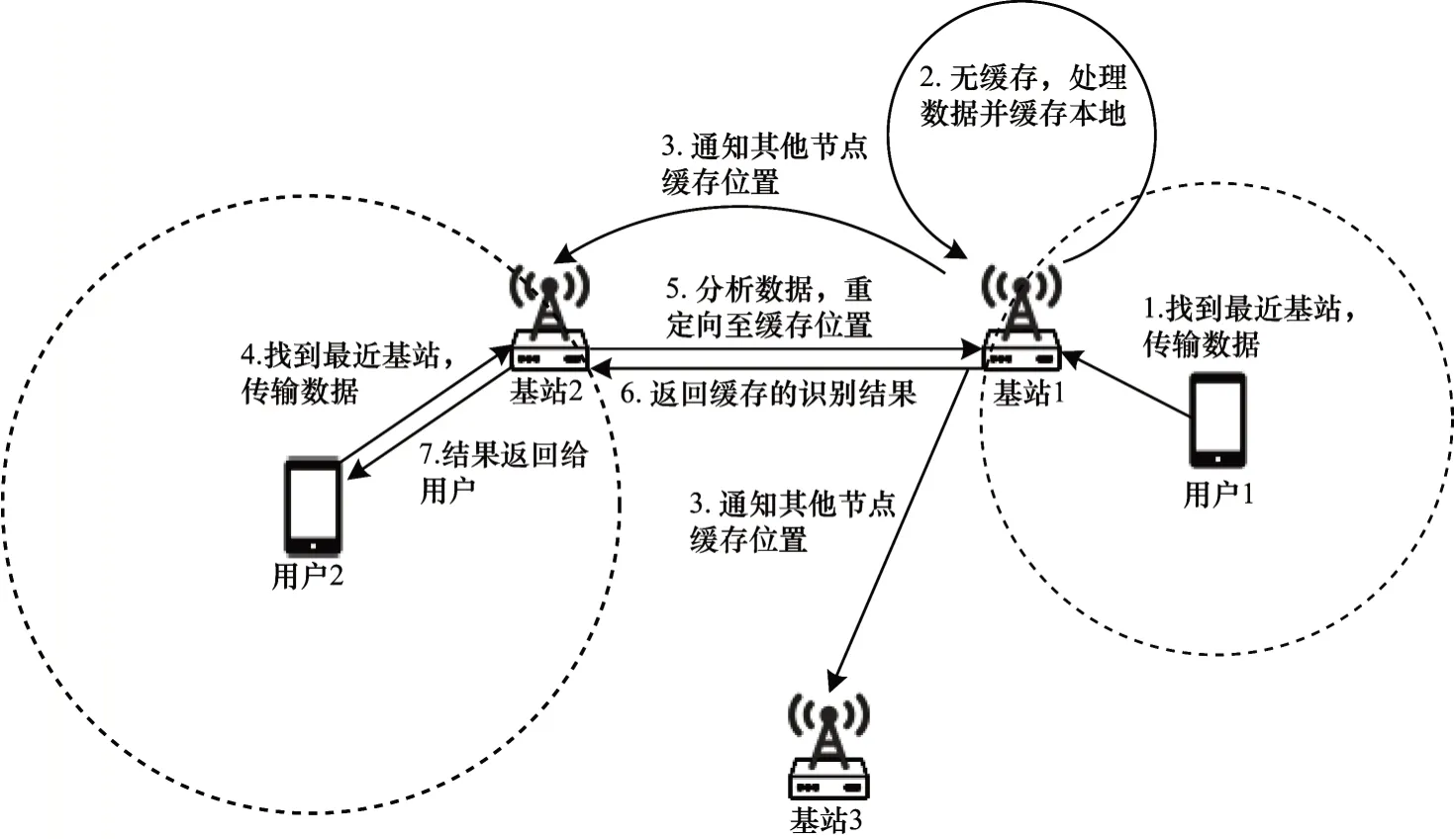
图1 一次典型的基于缓存的AR 任务执行过程Fig.1 A typical cache-based AR task execution process

2.1.2 全局缓存

要实现全局缓存，就需要全局节点通过一定方式保持同步。在本文构建的冗余消减模型中，全局节点自组织地形成一棵最小生成树（Minimum Spanning Tree，MST），每个节点只需要和父子节点周期性地发送保活报文即可维持此结构的正常运行。当节点离开或失效时，其父子节点就可以检测到，子节点直接连接到失效节点的父节点上。若根节点失效，则从根节点的子节点中随机选取一个作为根节点。在每个节点中维护一张如表1 所示的缓存表，以保存符合某些特征的数据是否已经被计算过并缓存至所在的节点。节点接收到新的请求时，会先查询这张表以获取缓存信息。若没有缓存，节点经过计算生成新缓存之后，它会通知其父子节点递归地更新所有节点的缓存表，具体过程如图2 所示。

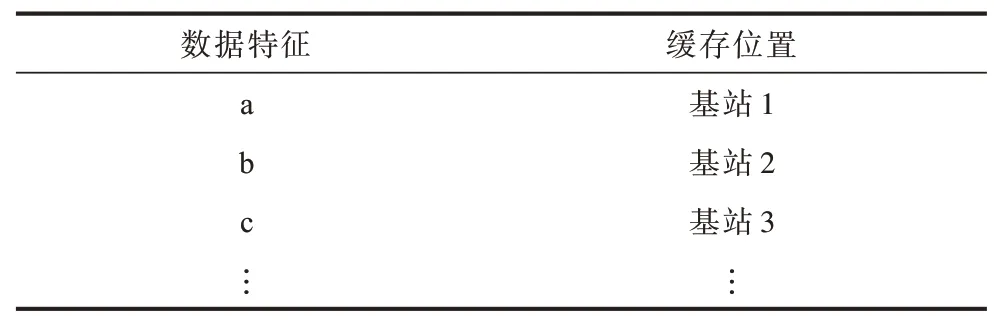
表1 全局缓存的缓存表Table 1 Cache table for global cache

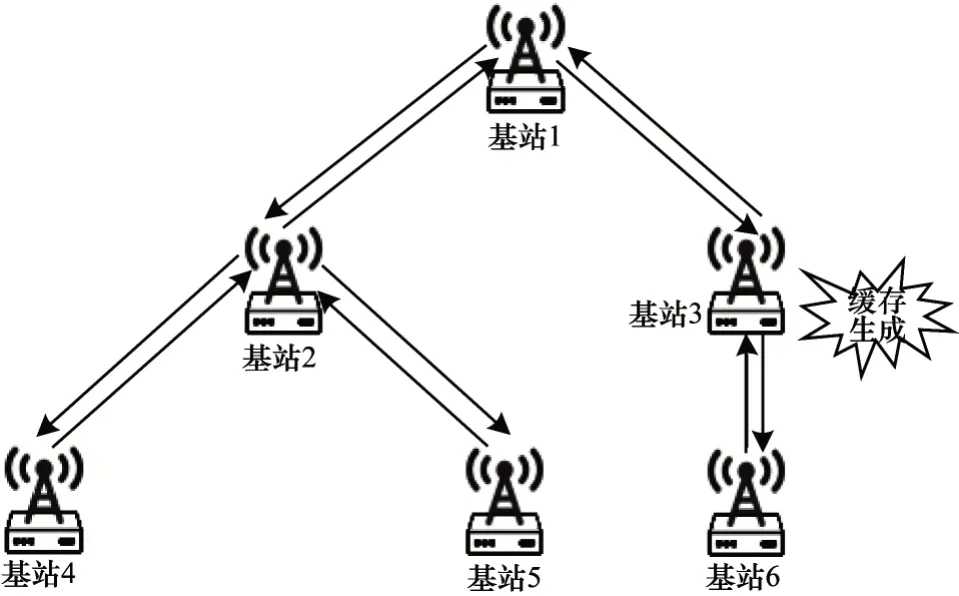
图2 缓存更新示意图Fig.2 Schematic diagram of cache update

2.2 请求时延

由于信号随着距离增加而衰减，因此基站的服务范围通常情况下是一个以基站为圆心的圆。本文设基站的有效服务距离为r，即在半径r内的用户都可以接收到该基站的有效服务。同样地，位于基站覆盖范围内的用户在收发数据时也会受到距离的影响，考虑到坐标是一个多维信息，因此，用向量来表示用户与基站的位置，使用函数dist(x，y)来表示两个坐标向量x与y的距离。

AR 识别任务往往是一个计算密集型任务，因此，一个边缘服务器所具有的CPU 核心数、主频以及GPU 时钟速度、内存总线容量等计算资源参数对于AR 任务的效率起到重要作用。考虑到相关参数往往是整数，本文把计算资源抽象为一个正整数c。

在AR 识别请求中，输入的数据通常为图像视频信息。不同设备、不同用户在进行AR 识别时分辨率和图像大小往往各不相同，因此，定义变量s表示请求的数据量大小。

对于一个位置为y且计算资源量为c的边缘服务器，当它收到一个来自位置x且数据量为s的请求时，其请求时延可能出现以下两种情况：

1）若请求数据已在服务器的缓存表中，则可以直接获取计算结果，此时用户时延包括数据传输时延与获取结果时延两部分。数据传输时延表示为μs·dist(x，y)，时延与数据量、距离成正比，其中，μ为比例系数。获取结果时延定义为一个较小的常量η，因为获取计算结果时，无论是返回本地结果还是返回其他服务器结果，开销都很小。

2）若请求数据不在服务器的缓存表中，则节点需要先对请求数据进行处理并缓存，然后将缓存结果返回给用户，此过程的时延包括数据传输时延和数据处理时延。数据传输时延与上一种情况相同，为μs·dist(x，y)。数据处理时延定义为λ·，即处理时延与任务量成正比，与计算资源量成反比，其中，λ为比例系数。

2.3 用户轨迹

对现有基站和云服务器的数据进行分析，得到AR 用户的历史轨迹数据集U={X，S}，其中，X为所有请求的位置信息，X={x1，x2，…，xn}，S为所有请求的任务量，S={s1，s2，…，sn}。数据集包含n个请求，按照时间先后顺序排序，第i个请求的发出位置为xi，数据量为si。

此外，通过对历史AR 用户识别任务数据进行分析，可以得到识别任务结果重用的相关信息。本文将相互之间可以重用识别结果的请求称为同一类别，从而可以得到κ×n的分类矩阵K，其中，总类别数为κ，矩阵元素取值为：

对于属于同一类别的识别请求，其识别目标往往是相同的，如同一个路口、同一家商店等，显然这样的请求属于且只会属于一个类别，即：

对于每一个类别，系统会在最早的请求到来时计算一次，之后就可以直接返回缓存结果。考虑到每个类别第一次请求的特殊性，本文定义gi为第i类中第一个到达的请求。而数据集按照时间先后顺序排序，因此，即第i类中使得Kik=1 的k最小者。

2.4 节点部署

根据收集到的用户轨迹信息，需要对边缘服务器节点部署位置进行决策。因为是在现有基站基础上新增功能，所以拥有候选基站位置集合L={l1，l2，…，lm}，并且可以认为这些基站覆盖了所有的请求位置，即对于任一请求位置，必定存在一个基站到它的距离小于等于r，也即：

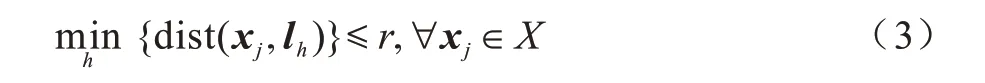
因此，需要决策的就是在各个节点上分配的计算资源量C={c1，c2，…，cm}（∀1≤h≤m，ch∈N，ci=0 表示此处不会部署边缘计算节点）。笔者希望在有限的部署代价之内尽可能提升用户体验，因此考虑了部署开销与用户时延。

部署开销指为每个候选基站要部署特定计算资源量所付出的代价。因为不同的基站位置不同，具体情况也不尽相同，所以用集合D={d1，d2，…，dm}(di＞0)来表示在各基站部署单位计算资源所需代价，其中，dh表示在基站h部署1 个计算资源所需代价。为使部署开销处于可控范围内，设定：

其中，R为总部署代价上限。

2.5 总时延优化

请求平均时延应当尽可能地小，以提升用户体验。由于请求数量为常数，因此等价于让所有请求的总时延最小，本文将其定义为：

其中，Tu为未命中缓存的总时延，Tc为命中缓存的总时延。

未命中缓存的总时延即K中所有类别第一次计算耗时，因此，要对每个类别i分别计算其第一次请求即gi的时延。当缓存未命中时，计算要在被请求的服务器本地完成，而被请求的服务器就是距离请求j位置最近的部署了边缘服务器的基站，因此，基站序号为。根据2.2 节，计算时延和数据传输时延分别可按照λ·与μs·dist(x，y)计算，如式（6）所示：

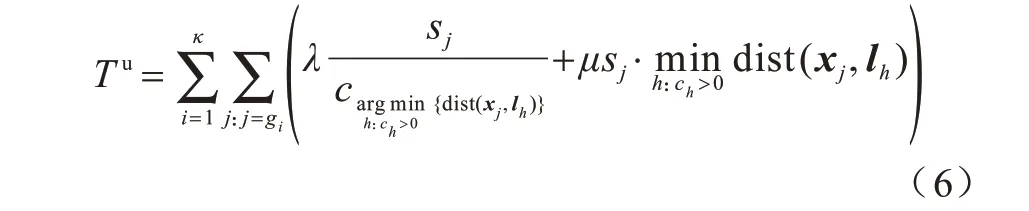
命中缓存的总时延为同类别中第一次到达请求之后的请求时延之和，因此，需要计算各类别中所有序号大于gi的请求时延。根据2.2 节，命中缓存的时延包括传输时延和获取结果时延，如式（7）所示：

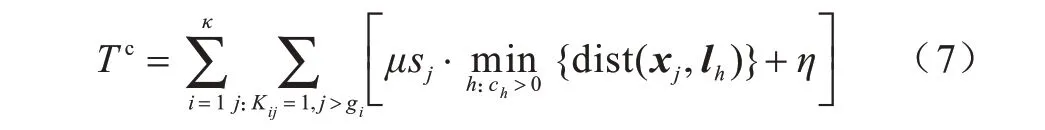
因此，所有请求总时延为：

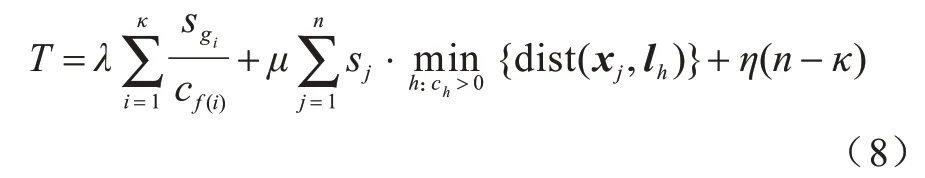
本文的优化问题描述为问题1：

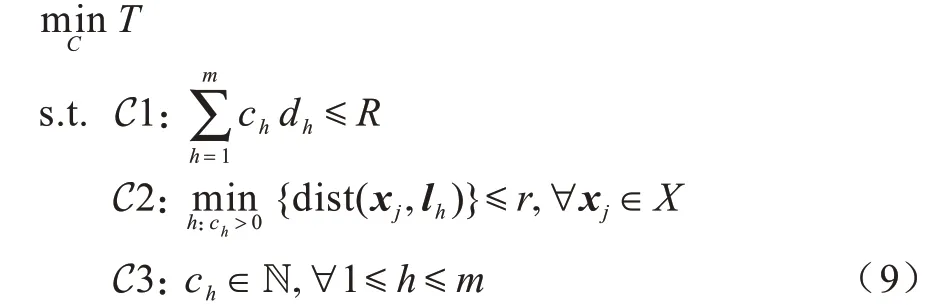
其中，C1 表示有限的可部署资源，C2 表示每个请求位置附近距离r内都存在一个边缘节点，从而确保所部署的边缘节点可以覆盖所有的请求位置，C3 表示可部署资源量为非负整数。

由于优化目标函数中的求最小值操作难度较大，因此本文考察原问题中的一种特殊情况，即所有基站均部署边缘节点的情况。修改优化问题1 的约束条件C3，确保每个基站都有可用的计算资源，如式（10）所示：

在此约束条件下，由2.4 节所述，基站集合L覆盖了所有请求，那么根据式（3），约束条件C2 永远成立，同样地，f(i)就变为与自变量C无关的函数f(i)=，则优化目标T变为：

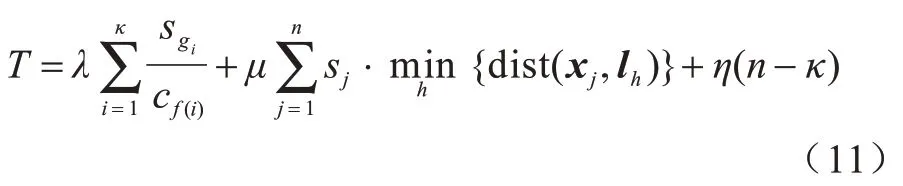
式（11）中唯一与自变量C相关的就是第1 项，且只需决定cf(i)的取值。令表示基站h所收到的所有第一次请求任务量之和，F={f(i)|1≤i≤κ}表示所有类别中第一次到达的请求所指向的基站的集合，则对于不在集合F中的基站h确保ch＞0，这样即得到简化的优化问题，即问题2：

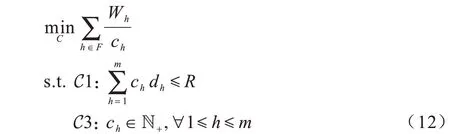
3 中小规模场景下的时延优化算法

针对一个城市，所研究的任务与位置密切结合的MAR 应用场景往往局限于少数区域，如AR 导航可能集中在一些特定的复杂路口或繁华的中心地带，AR 商场购物可能集中在购物中心区域。在一个请求量较为稀疏的较小范围内，基站数量m与最大代价R都不至于太大，此时可以基于动态规划构造伪多项式算法求得问题2 的最优解，从而得到与问题1 最优解接近的解。

3.1 问题简化

根据上文分析，在从问题1 到问题2 的转化过程中，可以直接使所有基站都至少部署最低的计算资源量以简化优化目标函数，但需要对集合F中的基站进行优化，所以，直接使不在F中的所有基站计算资源量为最低即可，即令h∉F的ch为大于0 的最小整数1，此处令：

设|F|为F集合中元素的个数，那么求解问题2 就只需要确定ch(h∈F)的值，上文定义了F={f(i)|1≤i≤κ}，但由于可能会有多个类别的第一次请求访问同一个基站，因此对F中元素按照基站序号从小到大排序，得到F={F1，F2，…，F|F|}，F1＜F2＜…＜F|F|，那么cFu就是基站Fu所具有的计算资源量，WFu就是基站Fu接收到的所有第一次请求的任务总量。

由于分配给不在F中的每个基站的计算资源量均为1，因此对于F中基站的计算资源分配问题总的可付出代价就要从R中去除，因此，新的可付出代价为

由此得到一个只需对ch(h∈F)进行决策的新问题，即问题3：

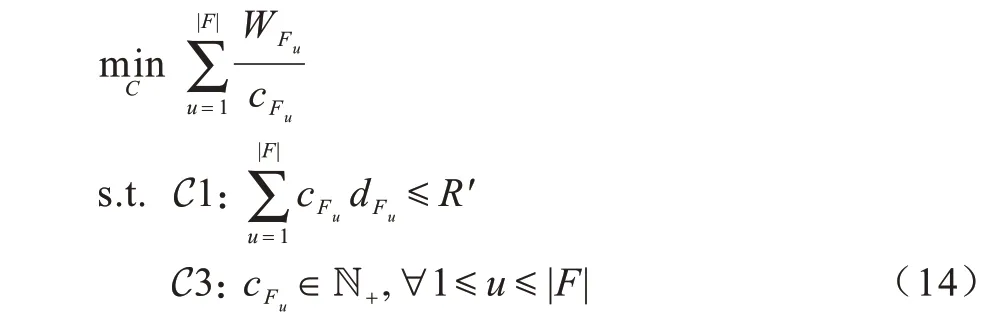
其中，WFu＞0，dFu＞0，R′＞0，∀1≤u≤|F|。

3.2 最优子结构

观察发现问题3 具有最优子结构，即解为(cF1，cF2，…，cF|F|)，资源总量为R′的问题3 的最优解可以由解为(cF1，cF2，…，cFk)(1≤k≤|F|)资源总量为r(1≤r≤R′)的规模更小的问题3 的最优解构造得到。本文用(|F|+1)×(R′+1)二维数组a保存子问题的最优解（ai，j表示解为(cF1，cF2，…，cFi)、资源总量为j的子问题的最优解），用二维数组p保存子问题的最优解的值（pi，j表示ai，j相应的最优解的值）。

对于ai，j与pi，j的子问题，可以将其理解为：有i个基站分配总量为j的资源，一个基站的资源量越大则其服务时延越低，本文目标是使它们的总服务时延最低，解(cF1，cF2，…，cFi)即为各基站资源的部署量。基于只有（i-1）个基站的子问题，可以通过遍历所有可能的新加基站（即基站i）的数量，得到有i个基站的问题的最优解，因此，有：

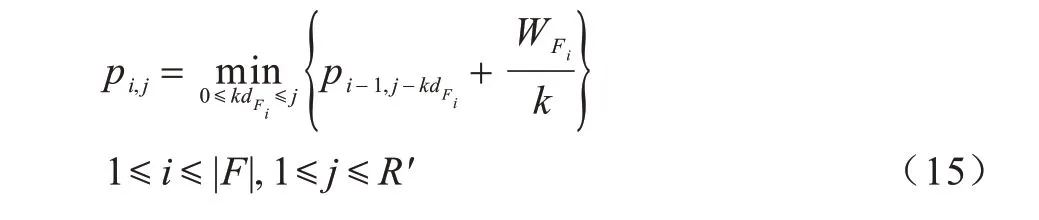
需要注意的是，所有的索引都从0 开始计，p0，·与p·，0、a0，·与a·，0为特殊情况。此外，还约定当分母k=0时

对于使式（18）取得最小值的k，问题3 的最优解可以直接通过在ai-1，j-k之后增加cj=k得到：

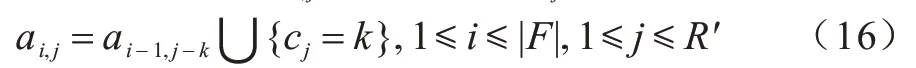
3.3 算法构造

问题3 与普通非线性背包问题的不同之处在于，问题中除了决策变量以外，参数均为实数而非整数。但是对于中小规模的输入，可以通过将dFi与R′同乘以10、100 或1 000 再四舍五入取整得到一定精度的近似解。此过程不涉及算法核心问题，因此，算法设计中默认前述参数是已经通过相关操作取整过的参数。

本文通过设计动态规划算法IDM（Integral Delay Minimization）对上述问题进行求解，如算法1 所示。首先对初始的特殊情况进行设置。对于m=0 的子问题，问题3 中F集合为空，解为空集，因此，目标函数值为0；对于m＞0 且R′=0 的子问题，目标函数中每一项分母均为0，即此基站资源量为0，那么服务时延为∞，故值初始化为∞。然后按式（18）和式（19）所示的状态转移方程从小到大计算p的值，得到|F|个解和资源量为R′的问题3 最优解。最后对不在F中基站的赋值，得到问题1 的解。

算法1IDM

3.4 时间复杂度分析

IDM 算法的时间复杂度分析如下：计算gi复杂度为O(κn)，计算Wh复杂度为O(κm)，构造集合F复杂度为O(κm)，对集合F进行排序复杂度为O(κlbκ)，动态规划最大次数为。因此，IDM 算法总时间复杂度为由于IDM 是一个伪多项式算法，因此该算法更适合在中小规模场景下求解。

4 大规模场景下的启发式算法

在一个用户终端密集、基站分布多的城市人流密集区域，数据集中的请求数量往往非常多，而基站数量也非常多，因此，总部署代价上限通常较高，这就导致动态规划算法会有很高的时间复杂度而不再适用，因此，本文研究大规模场景下的启发式算法。

4.1 大规模场景分析

大规模场景有如下特征：

1）请求量大。小规模场景中请求稀疏，相应类别较少，而大规模场景中会存在很多用户在很多位置发起请求的情况，这也导致其具有请求类别多的特征。当请求数n和类别数κ较大时，算法1 中为动态规划生成辅助变量过程中的时间复杂度O(κn+κm+κlbκ)就变得不可忽视。

2）基站密集，代价上限高。在小规模场景下，由于请求不多，因此稀疏部署的基站足以满足用户需求。在大规模请求场景中，为保证用户体验的流畅性，往往会部署很多基站，而该区域总可用代价也会很高。IDM 算法中动态规划的时间复杂度为这在基站数m和可用代价R很大时是不可接受的。

因此，在大规模场景下，应选择在用户平均时延目标不降低太多的情况下时间复杂度较低的算法。经过观察可以发现，对于本文所研究的服务与位置紧密关联的AR 识别任务，属于同一类别的任务往往是集中分布的，同类的任务集中在一个很小的区域中，而不同类的任务散布在整个区域中。IDM 算法在寻找每个类别执行计算任务的基站时，对所有基站都进行了遍历，但实际上距离一个类别较远的基站基本上是不可能执行该类别的计算任务的，尤其是在大规模场景中，基站分布较为密集，一个类别的计算任务必然在其附近的基站执行。

根据以上分析可知，在寻找每个类别执行计算任务的基站时，并不需要遍历所有基站。同样地，在为每个基站决定其计算资源部署情况时，也并不需要遍历所有请求。那么，就可以把所有请求与基站按照空间分布进行切分，从而得到多个规模较小的子问题，对于每个子问题使用IDM 算法求解后，再得到最终的解。

4.2 算法设计

考虑到子问题中的基站与请求应在空间上聚集在一起，因此本文通过聚类对原问题进行切分。因为数据规模较大且对聚类密度和层次没有特殊需求，所以本文选择具有线性时间复杂度的K-Means聚类算法。

通过构造启发式算法LDM（Large-scale Delay Minimization）来求解大规模场景下的问题，如算法2所示。对各个类别的请求计算它们的中心点，即同一类别所有请求位置坐标的均值，得到中心点集合A。将中心点集合A与基站集合L取并集并使用K-Means 聚类，得到具有φ个簇的聚类结果集合F，其中每个簇Fi包括该簇的请求集合与该簇的基站集合。据此，可以生成子问题的各基站位置集合Li′、各基站单位部署开销Di′、请求数据集Ui′中的请求位置集合Xi′、请求数据量集合Si′和请求分类矩阵Ki′。对于子问题的总部署代价上限Ri′，直接按照当前簇的基站数量占全局基站数量的比例来分配，Ri′=。至此，(Li′，Di′，Ui′，Ki′，Ri′)就形成了一个完整的子问题。

算法2LDM

上文2.4 节中提到，在解原问题的时候有一个最基础的假设——所有基站应该能够覆盖所有的请求位置。如果切分得到的子问题不能满足这一条件，那么就无法使用IDM 算法对子问题进行求解。因此，在得到子问题集合P之后，对各子问题进行检查，若存在基站不能覆盖所有请求的子问题，那么就对那些没有服务基站的请求进行搜索，查找距离它们最近的基站，将最近的基站所在子问题与当前子问题合并成为一个子问题。若被合并的子问题也不能满足覆盖条件，则递归地合并，直到满足覆盖条件为止。

经过覆盖条件检查与合并，对新的子问题可以分别使用IDM 算法求解。由于子问题之间相互独立，因此可以并行化完成求解这一过程，从而进一步加快本文算法的运行速度。子问题的解Ci就是子问题Pi内部对它们基站资源分配量的赋值，经合并即为最终对全局基站的赋值C。

4.3 时间复杂度分析

假设大规模场景中基站、请求都是均匀分布的，那么平均每个子问题的基站数量、请求数量都是原问题的。据此分析如下：计算各类别中心点集合为O(n)，K-Means 聚类的时间复杂度为O(κ+m)，构造子问题复杂度为O(n+m)。检查子问题覆盖条件整体时间复杂度为O(ξn)，其中，ξ为较小的常数。合并不满足覆盖条件的子问题为常数O(1)。求解单个子问题时间复杂度为则φ个子问题总的时间复杂度为综上分析，顺序执行LDM 的时间复杂度为，相比于IDM 的O(κn+本文通过线性时间复杂度的操作，使得IDM 的辅助参数计算部分效率提高了φ倍，动态规划部分效率提高了φ2倍以上。

5 实验与结果分析

本节分别模拟中小规模场景和大规模场景，对IDM 算法和LDM 算法进行实验分析，并使用直接均分和数值优化两种方法作为对比。直接均分法令所有m个基站chdh=，把总代价上限均分为m份，这样基站h的计算资源量为因为解必须为整数，所以此处进行了下取整。数值优化法通过数值方法迭代逼近原问题的最优解，但是无法得到整数解，可以一定程度上代表此问题的最优解。

5.1 实验设置

本节从研究场景和缓存模型两方面介绍模拟实验中的背景设置和相关参数。

5.1.1 研究场景

本文研究500 m×500 m 的矩形区域，以坐标（0，0）为左下角，以坐标（500，500）为右上角。该区域中已部署基站，每个基站的有效服务半径为100 m。在区域中随机产生AR 识别任务请求，任务可重用者为同一类别。因为同一类别往往产生位置相近，所以同一类别的请求坐标在区域中呈现标准差较小的高斯分布，这样同一类的请求就会在高斯分布的中心点附近集中分布，符合实际场景。此处设置标准差σ=5。不同类别的中心点在区域中均匀分布。考虑到实际场景中交付云计算的数据往往是图像，因此，设置随机生成的请求数据量范围为［1 MB，10 MB］，以表示图像的大小。在3.3 节IDM 算法设计中提到，在执行IDM 算法之前应当对基站部署单位计算资源的开销进行四舍五入取整，因此，本文设置每个基站部署1 个计算资源的开销为整数，在［1，10］之间均匀分布。

5.1.2 缓存模型

对于本文的缓存模型：设置计算时延参数λ=500，即在具有1 个计算资源的边缘服务器上计算1 MB的数据需要500 ms；设置传输时延参数μ=1，即在距离基站1 m 的位置向基站传输1 MB 的数据耗时为1 ms；设置缓存命中后获取结果参数η=3，即当请求数据的计算结果已在缓存中时，基站从收到数据，到用户获取到计算结果耗时为3 ms。

5.2 中小规模场景下的实验结果

本节按照中小规模的场景对IDM 算法进行实验测试。在此场景下，基站足以覆盖研究区域的大部分地区，但是较为稀疏，因此，设置基站数量为30 个且在研究区域中均匀分布。由于场景中请求不会太密集，因此设置请求数量为500 个。此外，由于各个类别的请求数量往往不相同，但单个类别的请求不会太多，因此设置每个类别的请求数量在［1，10］之间均匀分布。部署的总代价上限为500。本文将以此为基础，改变一些变量观察算法性能。

首先研究请求数量对于平均时延的影响，如图3所示。当请求数量较少时，请求可能集中地被少数基站处理，因此，直接均分会使很多不需要执行任务的基站分配到较多的资源，导致需要计算的基站资源减少，从而增加时延。之后随着请求数量提升，请求分布更趋均匀，基站的任务分配也更均衡，所以，时延会有下降趋势。IDM 算法的平均时延始终与数值最优的平均时延非常相近，保持在常数级的差别，由此可以看出IDM 算法对最优的逼近效果较好，对于请求数量的变化表现也很稳定。

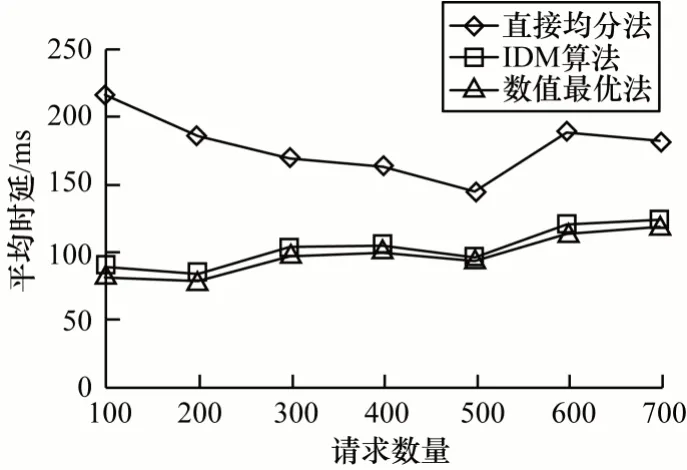
图3 中小规模场景下请求数量对平均时延的影响Fig.3 Influence of number of requests on average delay under small and medium scale scenarios

在部署计算资源过程中，总代价上限会对整体系统性能造成较大影响。如图4 所示，随着总代价上限的提升，3 种方法的平均时延均有所下降，而且不同部署策略之间的差异也会不断减小。这是因为当总代价上限提升时，各基站的计算资源逐渐充裕，由此部署策略对于总时延的影响也会减弱。可以看出，IDM 算法从最开始的与数值最优略有差距，直到总代价上限为900 时差距几乎消失，整个过程中两者的差距始终很小。

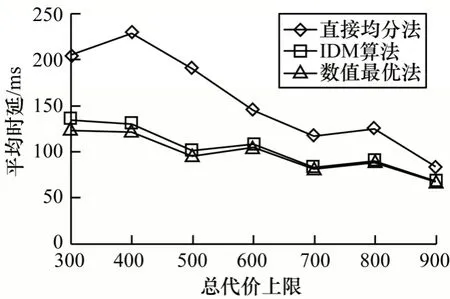
图4 中小规模场景下总代价上限对平均时延的影响Fig.4 Influence of limit of total cost on average delay under small and medium scale scenarios

5.3 大规模场景下的实验结果

本节对大规模场景进行模拟，测试LDM 算法的时延优化能力和执行时间。在1 000 m×1 000 m 的矩形区域内进行研究。大规模场景中基站往往较为密集，所以将基站数量增加到了300 个，是中小规模场景的10 倍，仍然均匀分布在研究区域中。大规模场景中请求数量也会很多，因此，设置请求数量为5 000 个。请求增多会带来类别的增加，但是每个类别中请求的数量往往不会有太多变化，因此，仍然设置每个类别的请求数量在［1，10］之间均匀分布。由于请求数很多，部署资源时的总代价上限也随之提升，本文设置为5 000。此外，LDM 算法本身有一个超参数φ用于调节子问题数量，设置为10。本文将以此为基础，变化一些参数观察算法性能。

考虑到请求数量是大规模场景中最重要的影响因素，因此本文研究在请求数量达到2 000 以上的情况下，随着请求数量增加各部署算法平均时延的变化情况，如图5 所示。可以看出：直接均分法的平均时延上升极为缓慢，基本不变；LDM 算法、IDM 算法与数值最优的平均时延都在缓慢上升，增长也越来越缓慢；当请求数量越来越多时，LDM 算法与数值最优的差距越来越小，不断逼近；在整个过程中，LDM 算法的平均时延都与数值最优相差不多。由此可见，LDM 算法更适用于存在大量请求的环境。

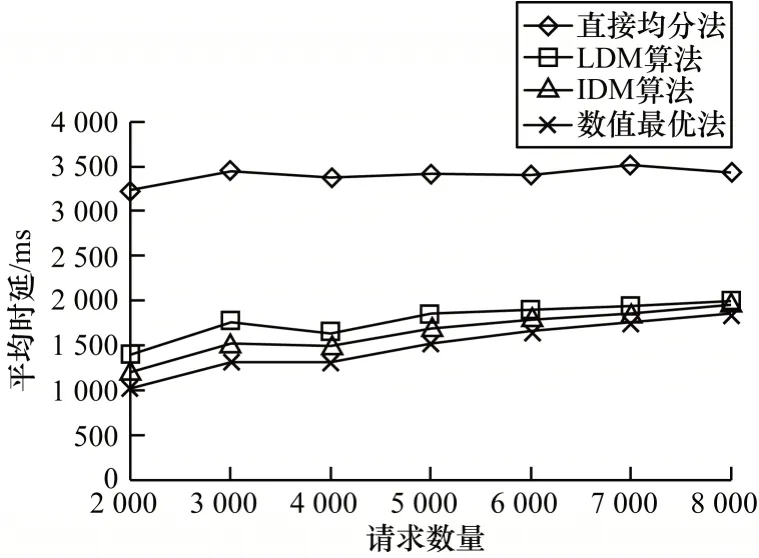
图5 大规模场景下请求数量对平均时延的影响Fig.5 Influence of number of requests on average delay under large scale scenarios

LDM 算法虽然平均时延略高于IDM 算法，但是算法运行时间远低于IDM 算法。在大规模场景下，IDM 算法处理5 000 个请求的平均时延为1 852 ms，运行时间为384 s，而LDM 算法完成同样的任务平均时延为1 696 ms，运行算法却只需7 s，其速度是IDM 算法的54 倍，而平均时延却只增加了9%，这无疑是值得的。如图6 所示：随着请求数量的增加，IDM 算法运行时间显著增加，而LDM 算法的运行时间却始终保持在非常低的水平。由此可见，LDM 算法对于大规模密集场景牺牲了少量的平均时延优化效果，却带来了大幅的运行时间缩减。

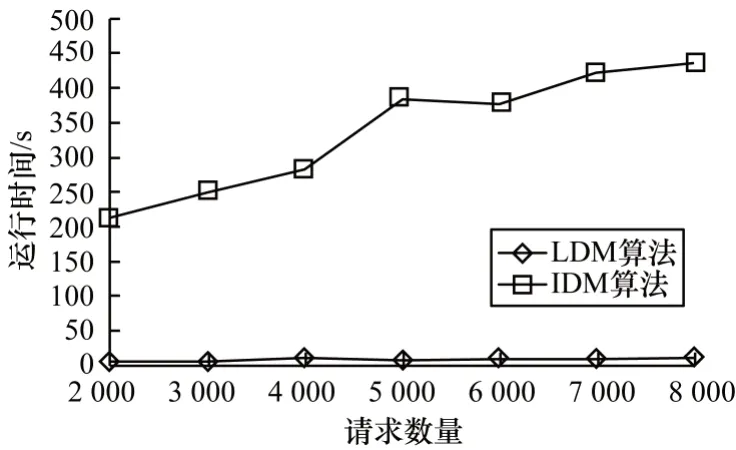
图6 大规模场景下请求数量对运行时间的影响Fig.6 Influence of number of requests on running time under large scale scenarios

6 结束语

本文以边缘计算为背景，研究基于冗余任务消减的AR 性能优化方法，针对AR 任务的冗余性，设计冗余消减的系统结构，包括节点本地缓存生成与管理、全局缓存同步等。以现有缓存系统为基础，对如何为基站部署边缘服务器的计算资源以最优化平均用户时延的问题进行建模，并借助动态规划的思想设计求解整数问题的IDM 算法。中小规模场景下的实验结果表明，IDM 的平均时延只比实数最优解增加5.85%。此外，对大规模场景进行分析，并借助分而治之的思想，使用K-Means 聚类将原问题切分成多个子问题用LDM 进行分别求解，以加快算法运行速度。实验结果表明，相比于IDM 算法，LDM 算法在平均时延只增加9.20%的情况下，运行时间下降了98.15%。下一步将以更准确的真实场景建模和online 任务调度为出发点对本文算法进行优化。