基于邻域归属信息混合度量的粗糙K-Means 算法

孙静勇，马福民

（南京财经大学信息工程学院，南京 210023）

0 概述

聚类算法根据数据之间的相似度对数据进行划分，使得簇内数据相似度高，而簇间数据相似度低。现有的聚类技术主要分为密度聚类、划分聚类、层次聚类、模型聚类以及网格聚类［1］。K-Means 算法［2］作为划分聚类算法之一，使用类簇中心点来代表每个类簇，具有简单、高效的特征，是当前研究的热门聚类技术［3-4］。

为解决不确定信息的划分问题，文献［5］将模糊集引入K-Means 算法，提出了模糊K-Means（Fuzzy K-Means，FKM）［6］聚类算法，在处理数据对象时采用模糊度量。文献［7-8］将粗糙集理论融入K-Means算法，提出了粗糙K-Means（Rough K-Means，RKM）［9］聚类算法，解决了传统K-Means 算法不能处理粗糙不可分辨信息的问题。文献［10-12］将粗糙聚类算法应用于林业、医学成像、Web 挖掘、超级市场和交通工程等不同领域。文献［13］使用相对距离作为粗糙K-Means 算法相似性度量的标准，减少了边界区域离群数据点的影响。文献［14］对粗糙K-Means 算法中上下近似权重问题进行了完善。文献［15］为验证粗糙聚类算法的有效性，对粗糙聚类算法和传统聚类算法进行了更进一步的对比讨论。

粗糙集和模糊集都是处理不确定信息的有效手段，两者之间具有一定的互补性。文献［16］结合了粗糙集与模糊集，提出粗糙模糊K-Means（Rough-Fuzzy K-Means，RFKM）聚类算法，利用模糊隶属度对数据点进行加权度量，使得算法在处理不确定信息时更加合理、准确。文献［17］提出的模糊粗糙KMeans（Fuzzy-Rough K-Means，FRKM）则认为处于类簇下近似中的数据点是确定属于该类簇的，只有处于边界区域的数据点与类簇具有不确定关系。文献［18］结合数据的空间分布对边界交叉区域的数据进行局部模糊度量，提出了基于边界区域局部模糊增强的πRKM 算法（BF-πRKM），提高了算法处理边界区域交叉严重数据的准确性。

通过加入粗糙集和模糊集，使得K-Means 算法在对边界区域的数据的处理更加合理、精确，但却忽略了数据局部密度对聚类结果的影响。文献［19］通过计算数据点邻域内的紧凑度来表示数据点的局部密度，使得局部密度越大的数据点获得的权值越高。文献［20］使用数据差异性度量数据的空间分布。文献［21-22］通过衡量数据点与类簇中心的距离，利用合适的映射函数使得距离类簇中心越近的数据点获得的权重越大。文献［23-25］结合数据点分布属性，对聚类算法的初始中心选取进行了改进。文献［26］结合距离与密度综合考虑了簇内不平衡问题，使用距离与密度进行综合度量，使得距离类簇中心越近且密度越高的数据点获得的权重越大。

上述算法虽考虑了簇内簇间的数据分布情况，却忽略了处于边界区域的数据点与各类簇中心的距离往往相差很小，而且相近数据点的邻域密度也差别不大，难以依据距离、密度进一步区分数据对象更偏向于哪个类簇。本文通过局部密度与邻域归属信息来描述数据点的空间分布，提出一种基于邻域归属信息混合度量的粗糙K-Means 算法（RKM-DN）。对数据点空间分布的衡量参考了数据对象的局部密度与邻域归属信息，下近似集中的数据通过局部密度衡量簇内不平衡分布，使得类簇中心尽可能处于簇内密度最高的区域，边界区域的数据通过其邻域归属信息衡量数据对象与类簇之间的相似性，以减少边界数据对类簇中心的位置的敏感度，提高算法对交叉重叠区域数据的划分能力。

1 相关聚类算法

1.1 粗糙K-Means 算法

RKM 聚类算法将交叉重叠区域中难以划分的数据点归为类簇的边界区域，在数据点划分的过程中，需要满足以下性质：

1）数据对象最多属于某一类簇的下近似。

2）若数据对象不属于任一类簇的下近似，则该数据对象属于两个及以上类簇的上近似。

3）若一个数据对象属于某一类簇的下近似，则该数据对象也属于该类簇的上近似。

在粗糙K-Means 算法中，待处理数据集D={xk|k=1，2，…，N}，其中，N为数据集中数据的个数，边域权值、下近似权值分别为wl、wb，wl+wb=1为类簇i的上近似为类簇i的下近似为类簇i的边域，vi为类簇i的中心点，算法根据数据对象到各类簇中心的距离将其划分到下近似或者边域中［9］。在每次迭代中，类簇中心计算公式如下［9］：

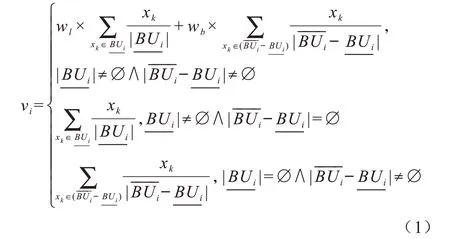
由式（1）可见，粗糙K-Means 算法在对类簇中心点进行计算时，将边界区域的数据整体赋予一个较小的权重wb，减少了边界不确定信息对类簇中心的影响。

1.2 改进的粗糙K-Means 算法

改进的粗糙K-Means 算法结合模糊集与粗糙集，使得粗糙K-Means 算法在对数据进行划分上下近似集的同时，还以模糊隶属度来衡量数据点对某一类簇的归属度。该算法在计算类簇中心时不仅考虑了类簇边界区域的数据点的计算，还兼顾了簇内数据对象分布不均的情况，计算公式如下［16］：

其中，K为聚类的个数，dki为数据点xk与类簇i的中心点的距离，m为模糊指数。

加入了模糊隶属度的粗糙模糊K-Means（RFKM）算法［16］的类簇中心计算公式如下：

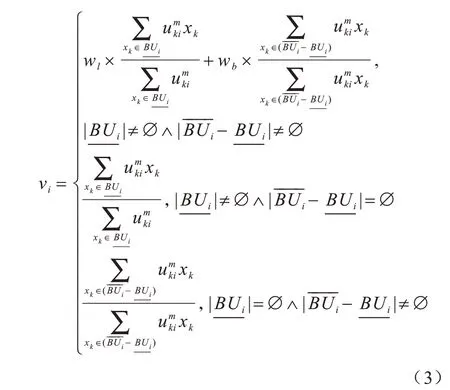
模糊粗糙K-Means 算法则认为处于类簇下近似的数据点是确定属于该类簇的数据点，因此其权值均为1。而处于类簇边域的数据点是不确定是否属于该类簇的数据，其权值使用模糊隶属度计算，模糊粗糙K-Means 算法的数据点权值计算公式如下［17］：

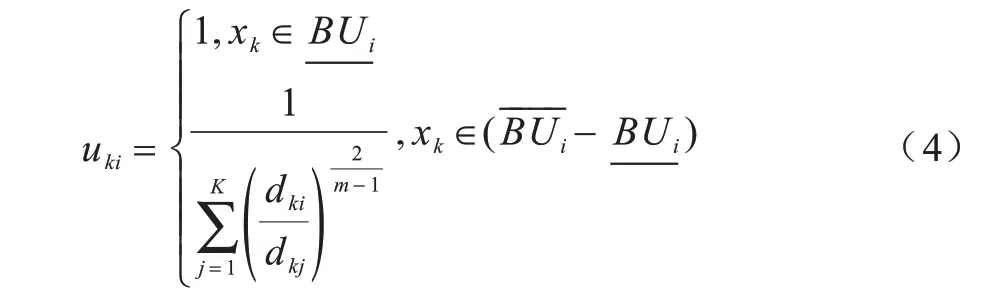
模糊粗糙K-Means（FRKM）算法对类簇中心的计算进行了改进，在计算类簇中心时不再需要人为设置上下近似参数，计算公式如下［17］：

由式（3）和式（5）可见，粗糙模糊K-Means 算法与模糊粗糙K-Means 算法在处理边界数据时使用模糊隶属度来衡量数据点之间的差异。

2 基于邻域归属信息混合度量的RKM 算法

2.1 局部密度和邻域归属信息度量

粗糙聚类算法对边界区域数据的衡量依赖数据点与类簇中心之间的距离，导致算法对边界区域的数据划分效果不佳，且边界数据对类簇中心的位置较为敏感。根据“簇内数据相似，簇间数据相异”的原则，数据点与其邻域数据对象具有较高的相似性。在没有先验知识的情况下，数据点的邻域数据包含许多信息。结合粗糙集属性对数据点邻域信息进行分析，可以得出以下特征：

1）若数据点xk的邻域数据均属于类簇i的下近似，则数据点xk属于类簇i的概率非常高。

2）若数据点xk的邻域数据既有属于类簇i的下近似，又有属于类簇i的边域，则属于类簇i的下近似的邻域数据占比越高，数据点xk属于类簇i的概率越大。

3）若数据点xk的邻域数据没有属于类簇i的上近似，则数据点xk属于类簇i的概率非常低（说明xk几乎不可能属于类簇i）。

如图1 所示，数据点x1与x2处于类簇交叉非常严重的边界区域，x1与x2同时属于类簇1、类簇2 与类簇3 的边域。通过观察x1的邻域归属信息可以发现，x1的邻域数据点多数分布在类簇1 中，少数分布在类簇3 中，仅有数据点本身处于类簇2 的边域中。因此，数据点x1属于类簇1 的概率要远大于类簇3 与类簇2。同理，数据点x2的邻域数据点多数分布在类簇2 中，少数分布在类簇3 中，仅有数据点本身处于类簇1 的边域。因此，数据点x2属于类簇2 的概率要远大于类簇3 与类簇1。

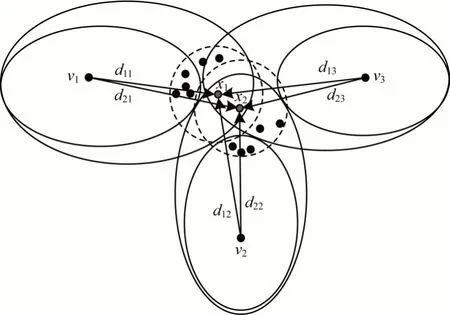
图1 邻域归属信息度量示意图Fig.1 Schematic diagram of neighborhood ownership information measure

由以上分析可以发现，即使是属于多个类簇的边界区域，数据点属于各类簇的可能性也不一致。在以上的数据分布中，使用距离或者密度对其进行衡量难以达到区分数据的目的，尤其是当数据点处于边界交叉严重的区域。通过观察数据点邻域内的数据分布情况，使用数据点的邻域数据点归属信息来衡量该数据点与类簇的相似性可以对数据的划分给予指导作用，从而提高算法的准确度。

如图2 所示，数据点x1与x2处于类簇1 的下近似，且x1与x2的邻域数据点均属于类簇1 的下近似，此时仅参考邻域归属信息难以区分x1与x2对于类簇中心的重要性。但类簇中心的位置应尽可能处于簇内密度最大的区域，因此，局部密度越高的数据点对类簇中心的贡献应越大。

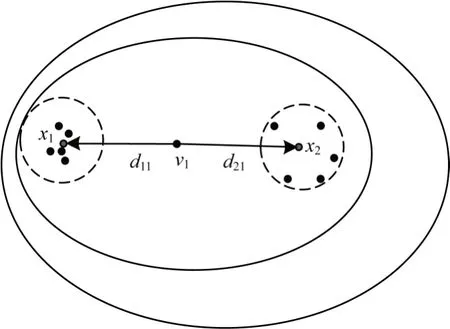
图2 邻域紧凑示意图Fig.2 Schematic diagram of neighborhood compact

由图2 可以看出，数据点x1的邻域数据点非常紧凑，大多围绕在x1的周围，而数据点x2的邻域数据点较为分散且与x2相距较远。很明显，数据点x1对于类簇中心的贡献更大。

根据局部密度与邻域归属信息度量，定义以下概念：

其中，|L(xk)|ξ代表xk的半径为ξ的邻域代表在数据点xk的邻域|L(xk)|ξ内属于类簇i的上近似的数据点个数代表在数据点xk的邻域|L(xk)|ξ内属于类簇i的下近似的数据点个数。

定义数据点xk与类簇i的相似度衡量公式如下：

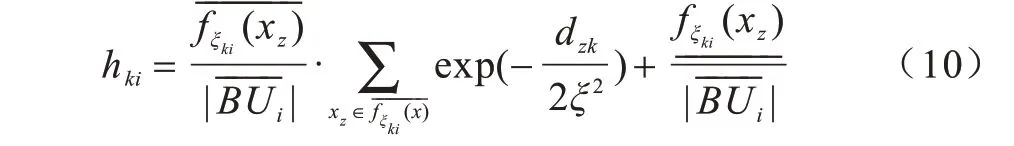
2.2 RKM-DN 算法

根据上文的邻域信息与局部密度分析，本节进一步提出考虑邻域点归属信息混合度量的粗糙KMeans 算法，其流程如图3 所示。

图3 RKM-DN 算法流程Fig.3 Procedure of RKM-DN algorithm

类簇中心计算公式如下：

算法具体步骤如下：

步骤1随机初始化类簇中心v。

步骤2∀xk∈D，计算xk到各类簇中心的距离。

步骤3根据距离矩阵计算上下近似集，∀xk∈D，将数据对象xk划分至距离最近的类簇i中｛dki=min（dki｜i=1，2，…，k）｝，若∃dki使得dkj-dki≤δ，则将xk划入类簇j的上近似集，否则将xk划分至类簇i的下近似集中。

步骤4∀xk∈D，统计xk在邻域范围ξ内的密度，统计数据点xk的邻域ξ内属于类簇i的上近似的数据点的个数，统计数据点xk的邻域ξ内属于类簇i的下近似的数据点的个数。计算xk在邻域范围ξ内的紧凑度并根据式（10）计算数据点xk的权重。

步骤5根据式（11）更新类簇中心。当算法达到最大迭代次数或者算法收敛时结束算法，输出划分结果，否则返回步骤2。

3 实验结果与分析

为验证算法的有效性，将本文所提算法在人工模拟数据集和UCI 数据集上进行实验。并与粗糙KMeans（RKM）［9］、粗糙模糊K-Means（RFKM）［16］、模糊粗糙K-Means（FRKM）［17］等算法在聚类精度和聚类时间方面进行对比。

3.1 人工数据集实验分析

随机生成服从正态分布的3 类数据，每个类簇包含50 个数据对象。为保证算法对比分析的公平性，在对同一数据集进行测试时所有算法均使用相同的初始聚类中心。在对算法参数进行设置时选择最优参数组合。其中，RKM 算法与RFKM 算法的下近似权重wl=0.9，边域权重wb=0.1，FRKM 算法的模糊指数m=2，RKM-DN 算法的邻域ξ=0.3，4 种算法的决策距离阈值为0.01，最大迭代次数为100 次。其聚类准确度与聚类时间结果如表1、表2 所示。

表1 人工数据集上的聚类准确度对比Table 1 Comparison of clustering accuracy on artificial dataset%

表2 人工数据集上的聚类时间对比Table 2 Comparison of clustering time on artificial datasets

由表1 可知，RKM-DN 算法在对人工数据集的聚类结果上最优，分别高出RFKM 算法1.33 个百分点，高出RKM 和FRKM 算法2.66 个百分点。但是在聚类时间上，由于RKM-DN 算法一次迭代的时间复杂度为，而RKM 等算法一次迭代的时间复杂度为O（N2），因此RKM-DN 算法相较于其他3 种算法所需时间较高。

为更直观地展示聚类效果，将4 种算法的聚类结果与原数据分布进行对比，图4 为人工数据集的分布，人工数据集共分为3 类，每类使用不同符号表示，其中，圆点代表第1 类数据，星号代表第2 类数据，倒三角代表第3 类数据。图5 给出了4 种算法在人工数据集上的聚类结果，加号为最终类簇中心，符号重叠的数据为类簇边界区域的数据。

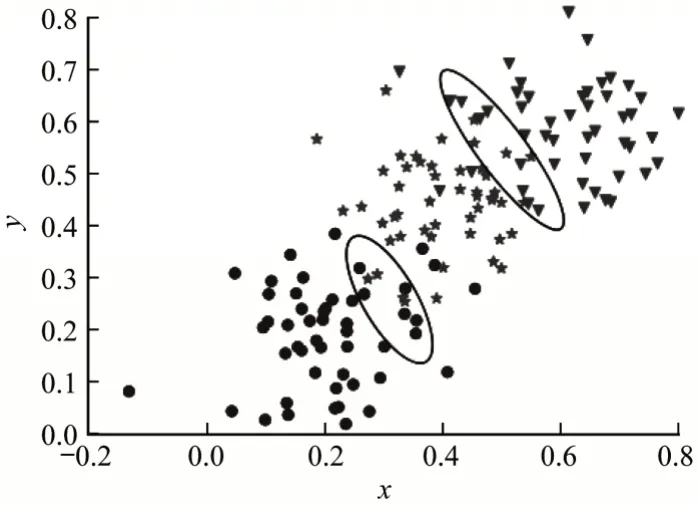
图4 人工数据集分布Fig.4 Distribution of artificial dataset

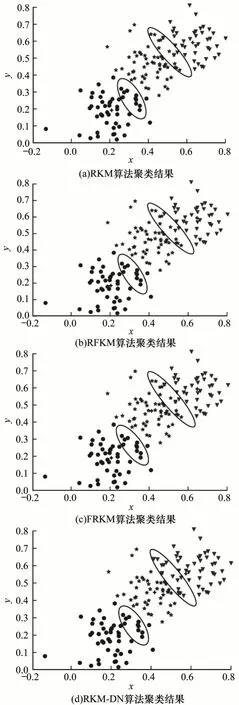
图5 4 种算法聚类结果示意图Fig.5 Schematic diagram of clustering results of four algorithms

从图5 可以看出，在对类簇1 和类簇2 边界区域的数据点划分时，RKM、RFKM、FRKM、RKM-DN 4 种算法的划分结果大致相同，均将图5 中所圈出的10 个数据点划分到类簇1 中。在对类簇2 和类簇3边界区域的数据点进行划分时，RKM、RFKM、FRKM 3 种算法的划分结果大致相同，而RKM-DN算法由于参考了数据点邻域内的邻居归属信息，从而误判率较其他3 种算法相比最低。

在图5 中所圈出的第2 类簇与第3 类簇的交界处共有13 个数据点，其中属于第2 类簇的有5 个，属于第3 类簇的有8 个。RKM 算法与FRKM 算法划分正确的数据点有4 个，划分错误的数据点有9 个。RFKM 算法划分正确的数据点有6 个，划分错误的数据点有7 个。RKM-DN 算法划分正确的数据点有8 个，划分错误的数据点有5 个。可以看出，在边界区域交叉重叠严重的地方，RKM-DN 算法相较于其他3 类算法具有较好的分辨能力。

3.2 UCI 数据集实验分析

在UCI 数据库中选取Iris、Wine、Breast Tissue、Fertility 4 类数据集进行分析。在对同一数据集进行测试时使用相同的初始聚类中心与初始参数。在对算法参数进行设置时选择最优参数组合，相关参数设置如表3 所示。由于Wine、Breast Tissue 数据集不同的特征值存在较大差异，因此在聚类前对其进行归一化。相关实验结果如表4 和表5 所示。

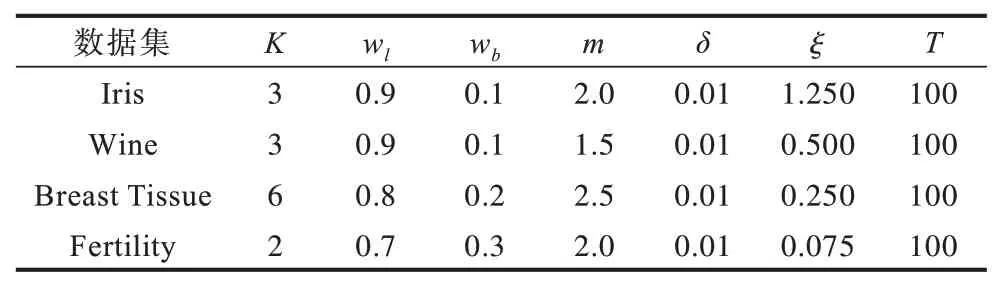
表3 算法参数设置Table 3 Algorithm parameter settings

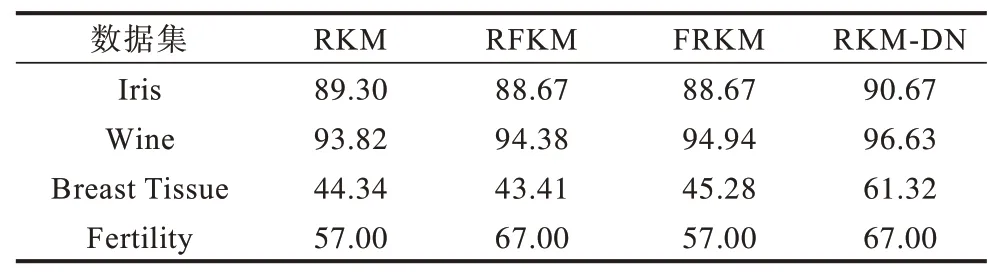
表4 UCI 数据集上的聚类准确度对比Table 4 Comparison of cluster accuracy on UCI dataset %

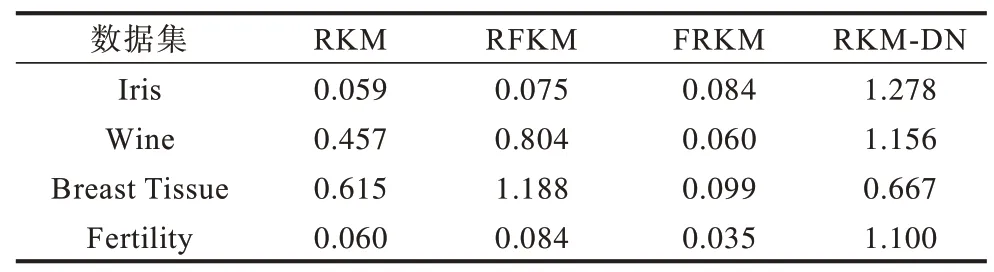
表5 UCI 数据集上的聚类时间对比Table 5 Comparison of clustering time on UCI dataset s

从实验结果可以看出，本文所提出的算法在Iris、Breast Tissue 和Wine 3 个数据集上的聚类准确率最高，在Fertility 数据集上的聚类结果与RFKM 算法相同，但在聚类时间上，其聚类所耗费时间较多。

以Wine 数据集为例，通过主成分分析法将Wine数据集映射至二维空间，其数据分布如图6 所示，第1 类数据使用圆点表示，第2 类数据使用星号表示，第3 类数据使用倒三角表示。图7 为4 种算法的聚类结果，其中，加号为最终类簇中心，符号重叠的数据为类簇边界区域的数据。结合图6 与图7 对4 种算法的聚类结果进行分析，在类簇1 与类簇2 的边界区域所圈出的区域中共有5 个数据点，这些数据点均属于类簇2。RKM 算法将4 个数据点划分至类簇1 中，将1 个数据点划分至类簇1 和类簇2 的边域中。RFKM 算法将4 个数据点划分至类簇2 中，将1 个数据点划分至类簇1 和类簇2 的边域中。FRKM算法将4 个数据点划分至类簇1 中，将1 个数据点划分至类簇2 中。RKM-DN 算法将4 个数据点划分至类簇2 中，将1 个数据点划分至类簇1 和类簇2 的边域中。因此，在类簇1 和类簇2 的边界区域的划分中，RFKM 与RKM-DN 算法的结果更加精确。

在类簇2 与类簇3 的边界区域所圈出的区域中共有7 个数据点，其中有6 个数据点属于类簇2，1 个数据点属于类簇3。RKM 算法将3 个数据点划分至类簇2 中，将1 个数据点划分至类簇2 和类簇3 的边域中，将3 个数据点划分至类簇3 中。RFKM 算法将1 个数据点划分至类簇2 和类簇3 的边域中，将6 个数据点划分至类簇3 中。FRKM 与RKM-DN 算法将4 个数据点划分至类簇2 中，将3 个数据点划分至类簇3 中。可见，在类簇2 与类簇3 的边界区域的划分中，FRKM 与RKM-DN 算法具有更佳的聚类效果。

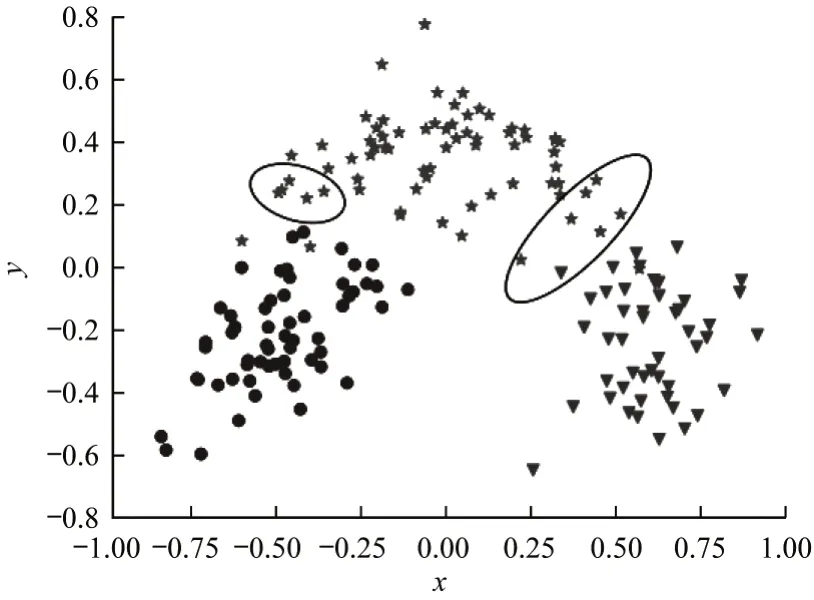
图6 Wine 数据集分布Fig.6 Distribution of Wine dataset

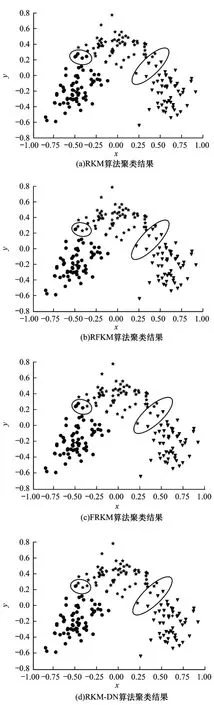
图7 Wine 数据集聚类结果示意图Fig.7 Schematic diagram of clustering results of Wine dataset

通过对图7（a）～图7（d）的分析可知，相较于原有算法，RKM-DN 算法对边界区域数据划分更加准确。这是因为在判断边界数据点与类簇相似度时，通过其邻域归属信息来衡量数据点对于各类簇的权重，使得算法更倾向于将边界数据点划分至与该数据点有更强的密度联通性的类簇中。更近一步，处于下近似区域的数据点与各类簇中心之间的距离差异较大，而边界区域的数据点与各类簇中心之间的距离差异很小，因此，将边界区域的数据点简单地依赖其与各类簇中心之间的距离进行模糊化度量，难以区分数据对象之间的差异性。如图7（d）所示，类簇2 的中心较其他3 种算法的聚类结果偏左，而在类簇2 与类簇3 的边界处，RKM-DN 算法依然能准确地对边界数据对象进行划分。这是因为RKM-DN 算法在对边界数据对象的权重进行计算时综合了邻域归属信息与局部密度，弱化了边界数据对类簇中心位置的敏感度，使得算法对边界区域的数据点划分更加合理，从而提高了算法对边界数据的划分能力。

4 结束语

基于粗糙集的聚类算法及其衍生算法在类簇不平衡时使用距离和密度等进行衡量，但当数据点处于类簇边域时，使用距离以及密度对数据点进行衡量较难区分数据的类簇。为此，本文提出一种考虑邻域点归属信息混合度量的粗糙K-Means 算法，通过数据点的局部密度以及邻域归属信息衡量数据点与类簇之间的相似性，提高了算法对边界数据的划分能力，并降低了边界数据对类簇中心点位置的敏感度。在人工数据集和UCI 数据集上的实验结果表明，基于邻域归属信息的混合度量方法可以有效提高粗糙K-Means 算法的聚类精度。