基于EEMD分解与相关系数的变压器振动信号特征量提取
徐舒蓉,刘君,曾华荣,吕黔苏,李堃,杨旗,赵莉华
(1.贵州电网有限责任公司电力科学研究院,贵州 贵阳,550002;2.南方电网有限责任公司防冰减灾重点实验室,贵州 贵阳,550002;3.四川大学电气工程学院,四川 成都,610065)
变压器振动信号的提取可实现与被采集设备无电气连接,并且具有较强抗干扰能力、灵敏度也比较高,因此基于振动信号的变压器机械故障诊断法是近年来变压器在线检测技术的研究热点[1-3]。
基于变压器振动信号的故障诊断技术研究主要包括有限元仿真建模与试验研究、信号处理两大方向。Berler等学者通过试验采集变压器空载、负载工况下的振动信号,通过分析其时域特征来评价变压器的线圈压紧情况[4];Belen Garcia,Juan Carlos Burgos 等学者定量研究了电网频率、电压与电流大小、温度等因素对变压器振动信号波形的影响规律,并分析了振动的传播路径变化情况[5-7];汲胜昌团队也研究了变压器振动与空载电压、负载电流的关系,并且通过仿真搭建变压器箱体振动信号传播模型,运用该模型初步成功诊断出绕组变形故障,验证了模型的有效性[8-14]。信号处理方面,傅里叶变换(FFT)是分析信号频域特征最基本的算法,反映了信号全局频率的分布[15-18],有研究者提出基于变压器振动信号基频占比以及高次谐波占比等作为变压器状态诊断的特征量[19-20]。随着信号处理技术的进一步发展,学者提出基于经验模态分解的希尔伯特黄变换和基于小波变换的时频分析法[21-22]。
需要指出的是,目前各研究者得出的结论因试验方法、测试条件、样品差异等因素导致其研究结果没有统一性,并且由于缺乏大量数据支撑而无法下定论,并且已有的研究基本只能实现正常、异常两种判断,对于利用振动信号判断变压器故障类型还亟须研究。
本文在相关学者的研究基础上,提出一种基于相关系数法与改进集合经验模式分解(Ense-mble Empirical Mode Decomposition,EEMD)的频率、峭度、幅值、均值等特征量提取方法。旨在为建立相对统一的变压器振动信号故障诊断方案提供理论参考。首先,根据实际经验设计滤波器对信号进行滤波,对滤波之后的振动信号进行EEMD分解得到一系列IMF(Intrinsic Mode Function,IMF)分量,运用相关系数法求取敏感IMF分量并对敏感IMF分量进行重构的信号处理方法,求重构信号的特征频率、峭度、幅值与均值特征量以构成特征向量。最后,运用该方法进行了试验变压器及不同故障状态下在运变压器的振动信号特征向量提取,研究其变化规律。
1 变压器振动信号试验数据采集
运用PCB 356A16压电式加速度传感器与NI9234数据收集仪采集型号为S11-M-10/10的试验变压器振动信号,设置采样频率25.6kHz。振动信号采集试验接线方法、信号采集点的布置分别如图1、图2所示。

图1 变压器振动信号采集接线图Fig. 1 Vibration signal acquisition system
如图1所示,通过调压器给试验变压器一次侧供电。图2中,将传感器分别布置在箱体顶部和正面三相绕组所对应位置,测试该试验变压器空载、负载工况下的振动数据。
对于在运电力变压器的振动信号采集,其油箱顶部位置是高压危险区,通常情况下将传感器安装于变压器正面。对于三相变压器,传感器分别布置在A、B、C三相中部位置;对于单相变压器,将传感器分别布置在变压器正面箱体的上、中、下三个位置。
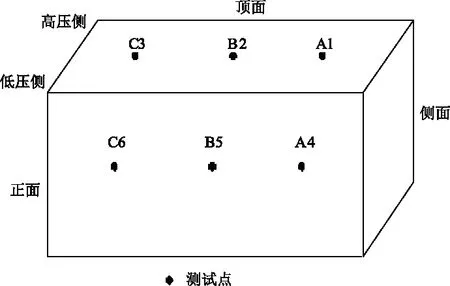
图2 变压器振动信号采集点的布置图Fig.2 Test point distribution map
2 EEMD分解算法、相关系数法
2.1 EEMD分解算法
2.1.1 EEMD分解过程
集合经验模式分解(EEMD)是一种将白噪声作为辅助来处理数据的方法[23-24]。其主要过程:在被分析信号中添加同样的高斯白噪声,利用高斯白噪声频域谱均匀分布的特点使待分析信号自动分布到适当的参考尺度中。然后,基于白噪声信号的零均值特点,经过多次平均使加入的白噪声消除,则整体平均值为最终结果。其中,待分析信号不会因此而发生改变[25]。
EEMD是EMD的改进算法,EEMD算法没有EMD经验模态混叠缺陷,但是却具有EMD自适应性、正交性、完备性等优点。EEMD算法分为如下几个步骤[26-27]:
(1)参数归一化:由待分析信号的标准偏差确定集成次NE、所需添加白噪声的幅值a。
(2)同样根据EMD算法对添加了白噪声后的信号xm进行分解:
xm=x+nm
(1)
式(1)中:nm为添加的白噪声,x为待分析信号。分解后的结果称为本征模函数(IMFs),记为ci,m,分解后余下的非零信号rm称为残余函数。
(3)然后,设置m=m+1,循环上述步骤(2),直到m等于初始时设置的集成次数NE。
(4)求取上述分解得到的IMFs总体平均值,该值即为EEMD分解结果。
2.1.2 EEMD参数设定
EEMD中最关键的两个参数是所添加白噪声的幅值a与集成的次数NE,EEMD分解结果的性能好与否与它们直接关联,因此需对其进行合理选择。集成的次数NE、白噪声的幅值a与标准差σ之间有关系[28]:
(2)
EEMD分解时,所添加的白噪声幅值越小,则分解得到的IMF分量与原始信号的误差越小;但是,幅值小,信噪比高,添加的噪声对极点的选取影响小,失去补充尺度的作用。应合理选择其幅值,一般a取0.2。在确定所添加白噪声幅值的情况下,集成的次数越多,则因噪声产生的误差越小。但是次数多计算量大,因此一般集成次数设置为100。
2.2 敏感IMF分量提取
信号经过EEMD分解后,会产生一系列IMF分量,各IMF分量与原信号的相关性各不相同,习惯把相关性强的IMF视为“敏感IMF分量”。在工程运用中,需挑选与原信号相关性强,即承载主要信息的敏感IMF分量进行分析。本文根据IMF分量与原信号相关系数的大小得到敏感IMF,相关系数>0.5则认为是敏感分量[29-30]。
2.3 振动信号特征量的选取
本文选择特征频率、峭度、幅值和均值作为振动信号的特征量。
(1)特征频率(fc)
理论研究表明,变压器铁心、绕组线圈振动信号基波频率为100Hz,由于非线性影响因素导致200Hz、300Hz等倍频分量的产生。当变压器铁心和绕组故障时,主频率发生变化,因此本文将振动信号频谱中幅值较大的频率定义为特征频率。
(2)峭度(k)
峭度实质为一个数学统计量,可以体现波形的尖峰度,为无量纲参数。峭度一般用字母k表示,其定义式如公式(3)所示[16]:
(3)
其中,μ为信号x的平均值,σ为信号x的标准差,E(t)为变量t的期望值。当变压器状态发生改变时,其振动信号时域波形的尖峰度k也会出现相应的变化。
(3)幅值(m)
变压器振动信号是周期信号,其幅值m也是一个重要参数(单位是g,即重力加速度),变压器运行状态异常情况下,幅值也会发生变化。
(4)均值(q)
对于变压器振动信号,均值可体现波形的对称程度(单位为g),正弦信号均值应该为0,信号均值越趋近0则说明该信号畸变较小,即正、负半周对称性较好。
2.4 特征量提取流程
基于快速谱峭度图法、EEMD分解、相关系数法的变压器振动信号特征量提取流程如图3示,其流程为:
(1)根据实际经验理论设计滤波器对信号进行滤波。
(2)对(1)中滤波后的信号进行EEMD分解,得到一系列IMF分量。
(3)运用相关系数计算法获取各IMF分量与原信号的相关系数大小,取系数>0.5的分量为敏感IMF分量。
(4)重构(3)中的敏感IMF分量,求重构信号的特征频率、峭度、幅值、均值特征量,构成变压器振动信号特征向量。
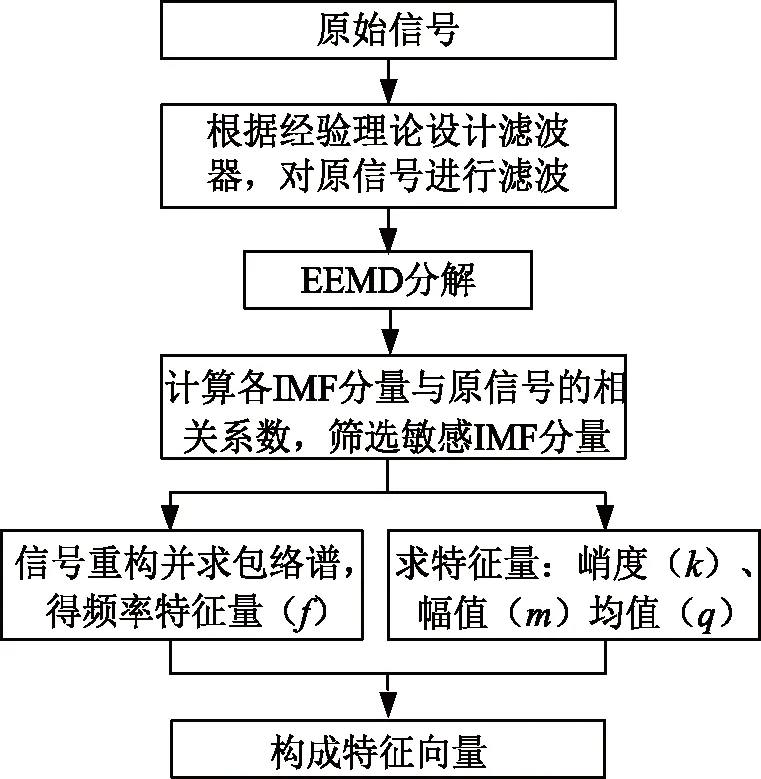
图3 特征量提取流程图Fig.3 The flow chart of feature extraction
3 试验变压器的振动信号特征向量提取
3.1 正常振动信号特征量提取
提取试验变压器空载振动信号特征量,空载时二次绕组无电流,一次绕组电流很小,此时主要为铁心振动。由图2可知,位于正面中部的第 B5测点以最短路径获取高、低压侧的振动信息,为最佳监测点。这里对B5测点的信号进行分析,图4展示了振动信号的原始波形、频谱。
由图4可知,铁心振动信号波形畸变较严重,存在<50Hz的低频干扰分量及少量基频的倍频分量,这是由于环境中干扰信号叠加以及铁心材料非线性导致。
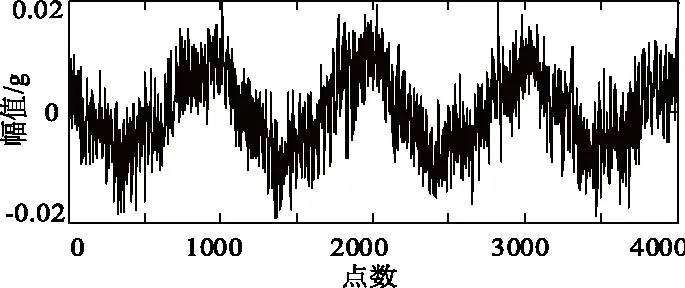
(a)原始波形(a) Original waveform

(b)原始波形频谱(b) Spectrum of oringinal waveform图4 B5测点振动信号原始波形与频谱图Fig.4 The original signal waveform and spectrum of vibration a B5
以B5测点振动信号的4000个数据为一个数据段,根据实际经验理论设计滤波器对原信号进行滤波,图5为滤波后的信号波形,对该波形进行EEMD分解,得到图6所示的一系列IMF分量。表1为IMF分量与原信号的相关系数值。
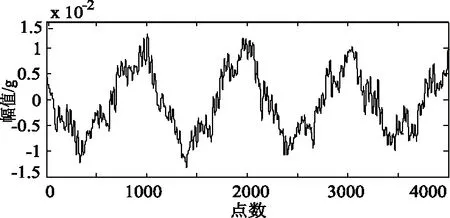
图5 滤波后的振动信号波形Fig.5 Signal waveform after filtering

(a)IMF1~IMF6 (b)IMF7~IMF12图6 重构信号的EEMD分解后得到的IMFFig.6 The decomposition IMFs using EEMD
据表1可选取相关系数>0.5的IMF6、IMF7、IMF8这三个分量为敏感分量。根据三个分量对信号进行重构并求包络谱,图7为重构后的波形。

(a)重构后的信号波形(a)Reconstructed signal waveform

(b)重构信号频谱(b)Reconstructed signal spectrum图7 重构信号波形及重构信号频谱图Fig.7 Reconstructed signal waveform and reconstructed signal spectrum
据图7可知其时域波形比图5更平滑、清晰;该变压器空载正常运行时的特征频率fc=100Hz,消除了原始信号频谱图中存在的低频干扰,其能量聚集性更高。最后求该重构信号的峭度k、幅值m、均值q,计算结果分别为:k=2.64,m=0.0069g,q=4.9×10-5g。综合四个参数构成试验变压器正常空载运行时振动信号的特征向量:
Tkz=[100 2.64 0.0069 4.9×10-5]
3.2 变压器铁心松动后空载振动信号
模拟变压器铁心松动故障,进行空载状态振动信号采集,同取B5测点进行分析。其原始时域波形及频谱如图8所示。由图8可知其时域波形与正常振动信号波形相似;但是其主频增大为200Hz。不仅存在低频干扰信号,并且包含高频干扰分量。
图9是滤波后的信号波形,同理,为了进一步消除低频干扰,对该信号进行EEMD分解,提取敏感分量进行信号重构。求得IMFs与原信号的相关系数结果如表1。

(a)原始波形(a)Original waveform
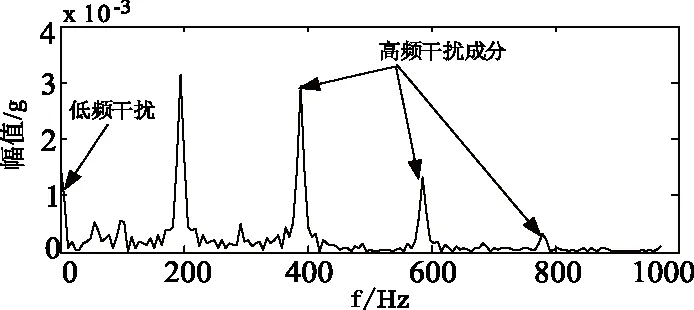
(b)原始波形频谱(b)Spectrum of oringinal waveform图8 故障状态原始信号波形与频谱Fig.8 The original signal waveform and spectrum in fault status

图9 空载故障振动信号滤波后信号波形Fig.9 The signal waveform after filtering

表1 IMFs与原信号的相关系数Tab.1 The correlation coefficient between IMFs and original signal
据表1可选取相关系数>0.5的IMF7、IMF8、IMF9为敏感分量对信号进行重构,并求其包络谱,结果如图10,由图10可知重构后的信号时域波形更加平滑,铁心松动变压器空载时的特征频率f=200Hz,存在400Hz等倍频分量。与图8中频谱图对比,消除了高频干扰成分,能量聚集性更好、倍频分辨率更高。计算得峭度、幅值、均值分别为:k=3.60,m=0.0083g,q=0.0004g。综上得试验变压器空载铁心松动故障振动信号的特征向量:
Tkzgz=[200 3.60 0.0083 0.0004]
与特征向量Tkz相比较,Tkzgz特征频率发生变化,峭度、幅值与均值呈增大趋势。
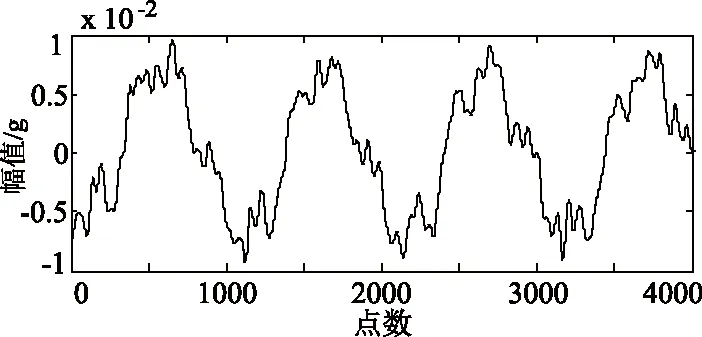
(a)重构后的信号波形(a)Reconstructed signal waveform

(b)重构信号频谱(b)Reconstructed signal spectrum图10 重构信号波形、重构信号频谱图Fig.10 The reconstruct signal waveform and its spectrum
3.3 试验变压器空载正常、铁心松动故障下特征量
综上分析,可将试验变压器正常、铁心松动故障状态下的空载振动信号的特征频率、峭度、幅值、均值构成的特征向量总结如表2所示。正常状态下,振动信号的特征频率均为100Hz,与理论相符;铁心松动故障时,特征频率增大为200Hz,100Hz幅值减小几乎减小为零,并且出现400Hz分量;其峭度值增大、振动幅值、均值都增大。可见通过用本文提出的方法求振动信号特征量,可判断该变压器出现异常。
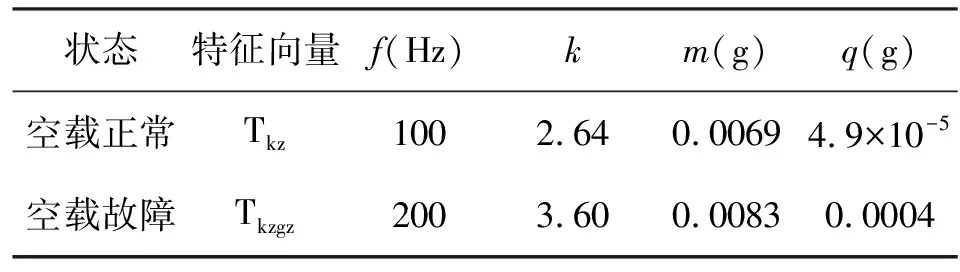
表2 试验变压器正常与故障状态下特征向量Tab.2 The eigenvectors of test transformer under normal and fault state
4 实际工程应用
4.1 铁心磁路故障
将本文提出的提取特征量方法运用到现场运行变压器中。对某变电站型号为ODFPS-250000/500 的500kV单相变压器正常状态与铁心磁路故障状态进行振动信号测试与分析。
4.1.1 正常运行状态下的特征向量提取
该变压器正常运行时原始时域波形与频谱如图11所示,其中100Hz的整数倍频信号较丰富,这与变压器负载率、温度、电流畸变率等影响因素有关。
滤波后的波形如图12所示。通过相关系数法选取EEMD分解后的敏感IMF分量,相关系数计算结果如表3。
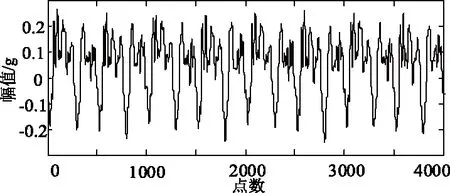
(a)原始波形(a)Original waveform

(b)原始信号频谱(b)Spectrum of oringinal signal图11 实际运行变压器正常振动信号波形及频谱Fig.11 The normal vibration signal waveform and frequency spectrum of an actual operation transformer

图12 滤波后时域信号波形Fig12 Signal waveform after filtering

表3 IMFs与原信号的相关系数Tab.3 The correlation coefficient between IMFs and original signal
由表3可选取相关系数>0.5的IMF5、IMF6、IMF7、IMF8这四个分量进行重构后并求其包络谱,结果如图13所示。与图11中原始频谱相比,经过滤波和重构后的频谱能量聚集性更好,倍频分辨率更高,消除了大部分低频与高频干扰成分。该变压器正常运行时特征频率范围是100Hz~500 Hz,主频为200Hz,400Hz与500Hz幅值也较大。在MATLAB中求得其峭度、幅值、均值分别为:k=2.73,m=0.169g,q=0.0001g。综上可得该变压器正常情况下的特征向量Tzc:
Tzc=[200 2.73 0.169 0.0001]

(a)重构后的信号波形(a)Reconstructed signal waveform

(b)重构信号频谱(b)Reconstructed signal spectrum图13 重构振动信号波形及重构信号频谱Fig.13 Reconstructed signal waveform and reconstructed signal spectrum
4.1.2 磁路故障运行状态下的特征向量提取
该变压器发生磁路故障下的振动原始波形与频谱如图14所示,发生磁路故障后的振动信号振动幅度变大,每个周期内的波形出现明显的尖峰;振动频谱成分变复杂,出现大量100Hz的倍频分量及50Hz的奇次倍频分量。

(a)原始波形(a)Original waveform

(b)原始信号频谱(b)Spectrum of oringinal signal图14 实际运行变压器磁路故障振动信号及频谱Fig.14 The waveform and spectrum of actual operation transformer vibration signal under magnetic circuit fault
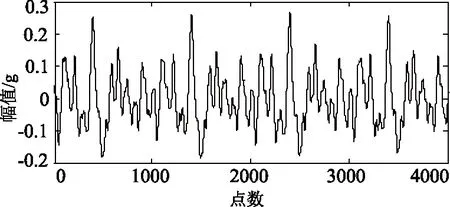
图15 滤波后的振动信号波形Fig.15 Signal waveform after filtering
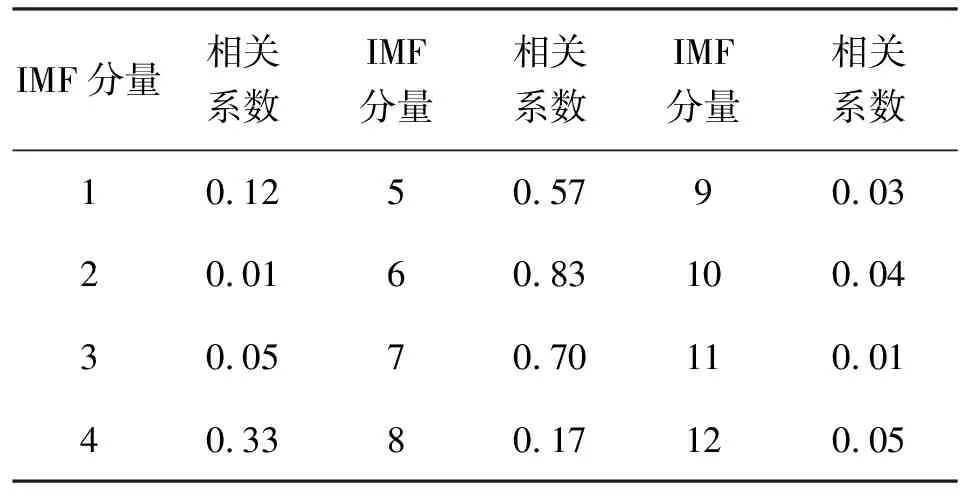
表4 IMFs与原信号的相关系数Tab.4 The correlation coefficient between IMFs and original signal
对原信号滤波之后的波形如图15,对图15中信号波形进行EEMD分解并求相关系数,结果如表4所示。
据表4可取IMF5、IMF6、IMF7为敏感分量进行重构并求其包络谱,结果如图16,可知重构信号去掉了部分相关性小的分量,该变压器磁路故障时,主频仍然为200Hz,但出现大量50Hz的奇次倍频分量,可判断这是该变压器磁路故障下出现的最具特征的频率成分,这里以(200Hz,250Hz)作为该故障状态下的频率特征。同理求得该重构信号的峭度、幅值、均值为:k=3.72,m=0.266g,q=0.0003g。综上所述得该变压器磁路故障下的特征向量Tclgz为:
Tclgz=[(200, 250) 3.72 0.266 0.0003]
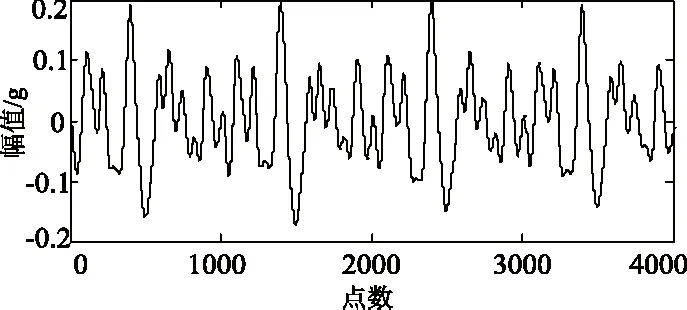
(a)重构后的信号波形(a)Reconstructed signal waveform
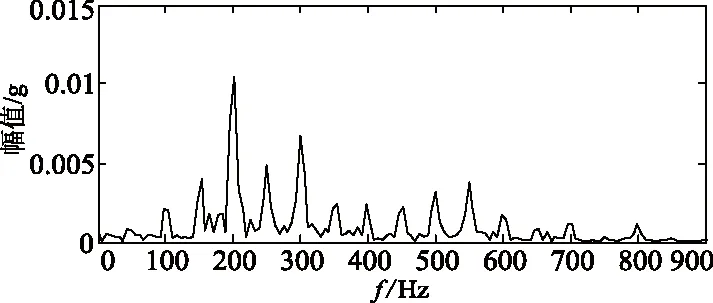
(b)重构信号频谱(b)Reconstructed signal spectrum图16 滤波信号、重构信号波形及重构信号频谱图Fig.16 Reconstructed signal waveform and reconstructed signal spectrum
4.1.3 实测变压器正常与磁路故障下特征向量对比
综上所述,得该变压器正常与磁路故障下的特征向量如表5所示。与正常状态下Tzc相比,Tclgz出现了250Hz频率特征,峭度增大1.01,振动幅值增大0.56倍,均值增大2倍。可将特征向量Tclgz可作为该变压器磁路故障的判据。

表5 实际运行变压器正常与故障状态下特征向量Tab.5 The feature vectors of actual operation transformer in normal and fault state
4.2 铁心多点接地故障
对某220kV变电站型号为SFPSZ10-1800 00/220的三相变压器正常状态与铁心多点接地故障状态进行振动信号测试与分析。
4.2.1 正常状态
运用本文处理方法对该变压器正常运行时振动信号进行滤波、提取相关系数并重构后的时域波形与频谱如图17。

(a)重构信号时域波形(a)Time domain waveform of reconstructed signal

(b)重构信号频域波形(b)Frequency domain waveform of reconstructed signal图17 重构信号波形及重构信号频谱图Fig.17 Reconstructed signal waveform and reconstructed signal spectrum
据图17可知,经处理后该变压器正常状态下该变压器时域波形清晰干净。主频为300Hz,低频幅值较大,大于400Hz的分量较少。计算其峭度、幅值、均值得其特征向量为:
Tzc=[300Hz 2.15 0.10 0.00075]
4.2.2 铁心多点接地故障
同理得到该变压器发生铁心多点接地故障时重构后的振动信号时域及频谱图18,可知故障后的信号波形存在较多毛刺、频率范围整体扩大,基频的倍频分量幅值明显增大并且主频为增大为500Hz,700Hz处的幅值也较大。计算其峭度、幅值、均值得铁心多点接地故障下的特征向量为:
Tgz=[500Hz 2.83 0.20 0.00115]
该故障情况下不仅主频增大,峭度、幅值、均值都增大。但峭度值变化较小。

(a)重构信号时域波形(a)Time domain waveform of reconstructed signal
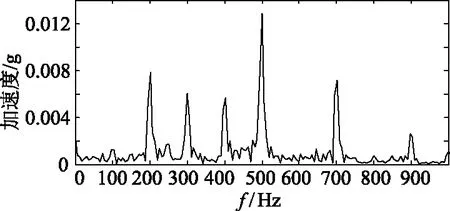
(b)重构信号频域波形(b)Frequency domain waveform of reconstructed signal图18 铁心多点接地故障重构信号波形及重构信号频谱Fig.18 Reconstructed signal waveform and reconstructed signal spectrum under Iron core multi-point grounding fault
5 结论
综上所述,本文运用一种基于相关系数法与EEMD分解的频率、峭度、幅值、均值等特征量提取方法,对试验变压器正常、铁心振动信号进行特征向量提取及分析,并将其运用到实际运行的变压器中,研究磁路故障、铁心多点接地故障下的特征量。得结论如下:
(1)EEMD克服了EMD模态混叠的缺陷,有效地将振动信号分解为不同频率的IMF分量;相关系数法可正确提取敏感IMF。经过滤波与重构后的变压器振动信号保留了重要分量,滤除了大部分的低频、高频干扰成分,使信号频谱能量聚集性更好,倍频分辨率更高。
(2)运用本文提出的特征提取流程对试验变压器空载正常、空载铁心松动状态下的振动信号进行分析,结果表明在该变压器空载时特征频率为100Hz,峭度值集中在2.0~2.6之间;空载铁心松动状态下特征频率为200Hz,峭度值、幅值与均值都增大;本文提出的特征量能有效区分变压器的故障状态。
(3)经实例研究分析可知在不同故障下,本文提取的特征向量中各参数均呈现增大趋势,但是其增大的幅度因故障类型而异。磁路故障时主频大小的变化不明显,但是峭度值变化较大;铁心多点接地故障下峭度值变化较小而主频则增大为500Hz;均值和幅值的增大倍数在不同故障状态下的差异不太明显。
综上,本文研究的变压器振动信号特征量提取方法不仅可判断变压器是否异常,并且有望区分不同故障类型的信号,进而实现变压器故障类型诊断,对实际工程中变压器的故障诊断具有一定的参考价值。

