数据异常情况下遥感影像时间序列分类算法

（1.石河子大学信息科学与技术学院，新疆石河子 832000；2.安徽大学互联网学院，合肥 230039）

0 引言

地球陆地是人类赖以生存和发展的物质基础，获取陆地表面各种资源及其变化数据是人类认识和利用陆地表面的前提。遥感技术通过人造地球卫星、航空、无人机等平台上的遥测仪器对地球表面实施感应遥测，产生了海量的不同空间分辨率和时间分辨率的遥感数据，这些遥感数据蕴含着地球表面各类地物在空间和时间上的巨量信息。如何精确地区分各类地物是研究陆地表面的基础性工作。遥感影像分类就是利用计算机通过对遥感影像中各类地物的光谱信息和空间信息进行分析，选择特征，将影像中各个像元按照某种规则或算法划分不同的类别，然后获得遥感影像中与实际地物的对应信息［1］。在遥感影像分类方面，对于常用的单时相遥感影像分类技术，只能利用波谱反射率的异同来分类，有效信息获取不足使得分类结果存在许多问题，比如混合像元的判定、“同物异谱，异物同谱”现象的存在、分类精度在时间和空间上难以保持稳定等。众所周知，地表事件的发生和地物的演化，是随着时间的推进而进行的，这使得地表覆被在时间上具有一定的变化规律。遥感影像反映出，大多数地物的波谱反射率经过长期观测可以重复获取，且由波谱反射率组成的时间序列表现出一定的周期性。遥感影像时间序列由于蕴含显著的物候信息，使得不同地物拥有不同的光谱反射率轨迹，利用这些数据特点能够更加有效地区分地物类型，时间序列在土地覆盖分类方面已经被证明优于单时相分类［2］。

随着深度学习的兴起，学者们提出了很多基于深度学习的遥感影像时间序列分类算法，常见的用于时间序列建模的深度学习框架包括长短期记忆（Long Short-Term Memory，LSTM）网络、门循环单元（Gate Recurrent Unit，GRU）、一维/三维卷积神经网络（1D/3D Convolutional Neural Network，1D/3D CNN）和时间变换网络（Temporal Transformer Network，TTN）等。利用LSTM 模型［3］的序列数据建模能力，文献［4］提出两种LSTM 模型（深度栈式LSTM 和深度双向LSTM）用于MODIS时间序列分类，分类精度优于随机森林（Random Forest，RF）和支持向量机（Support Vector Machine，SVM）分类方法。卷积神经网络自从被提出之后被广泛应用于各种遥感任务，包括陆地覆盖分类［5-6］、影像分割［7］、目标检测［8］、丢失数据重建［9］等。在这些遥感任务中，卷积神经网络通过对影像x维和y维进行卷积操作来利用影像数据的空间特征，也就是说卷积操作主要运用在影像的光谱域或者波段域，但没有考虑影像的时间特征。为了处理遥感影像时间序列数据，学者们又将卷积神经网络应用于遥感影像时间序列分类。文献［10］利用一维卷积神经网络［11-12］可有效描述一维序列数据的特性，提出基于一维卷积神经网络的农作物分类方法，实验结果表明该方法分类性能优于LSTM 和传统分类方法。文献［13］多尺度卷积神经网络（Multi-scale Convolutional Neural Network，MCNN）提取不同比例和频率的特征，将特征提取和分类合并在一个框架。文献［14］提出一种端到端的遥感影像时间序列分类深度学习算法，以一维卷积为核心构建3 个组件分别描述遥感影像各像素的波段间依赖性、全波段全卷积特征以及邻居像素特征来实现像素级分类，并在2017 年时间序列陆地覆盖分类挑战赛（TiSeLaC 2017）［15］获得第一名。由于深层LSTM形式的深层递归神经网络在这种像素较少的情况下，训练并不是很成功［14］，文献［16］利用多通道深度卷积神经网络（Multi-Channels Deep convolutional Neural Networks，MCDNN）体系结构通过在输入的每个维度上独立（即并行）应用卷积，来利用多模态时间序列数据的不同特征之间的假定独立性。指标值与反射率的测量值相关，文献［17］提出的时序卷积神经网络（Time Series Convolutional Neural Network，TSCNN）通过共同训练多元时间序列以进行更好的特征提取，从而获得了更好的分类结果。

现有的遥感影像分类算法严重依赖数据本身，而数据本身存在数据缺失、数据扭曲等数据异常问题。且现有分类算法大多针对某一个具体研究区，同类作物物候期相对变化很小，同类作物的时间序列数据组成像素对应的归一化植被指数（NormalizeD Vegetation Index，NDVI）等特征曲线高度相似，直接输入到分类算法中。实际上，同一种作物的物候期大体相似，但随年份和区域的不同呈现出多样性，因此对应的NDVI 等特征曲线也呈现出多样性特征。这种遥感影像中提取的与物候期相对应的特征曲线多样性可以通过扭曲操作来得到，即对特征曲线进行时间轴和特征值轴两个维度进行适度的平移、拉伸、压缩等操作，可以得到同一种作物的丰富多样的特征曲线。目前尚无学者关注数据扭曲情形下遥感影像时间序列分类算法的鲁棒性问题。文献［4］中提出遥感影像时间序列数据存在扭曲的现象，但采取了数据增强的方式进行解决，没有从模型和算法的角度来研究提高算法鲁棒性的方法。

为解决以上问题，本文的主要贡献有：1）提出了一种端到端的多模式与多单模式架构融合的网络，解决数据异常情况下时间序列分类问题；2）在基于卷积神经网络分类器中引入了能够提取单个波段和多波段特征的结构，在网络中结合多种特征进行时间序列分类，不仅仅是单靠其中一种；3）将模型应用到遥感影像时间序列分类中，取得了较好的效果。通过1D-CNN、MCDNN、TSCNN、LSTM 和本文的网络进行对比，对TiSeLaC遥感影像时间序列数据集进行分类，分别对数据缺失和数据扭曲两种数据异常情况进行分析。实验结果表明端到端的多模式与多单模式架构融合的网络在数据异常的情况下分类精度较高，F1值达到了93.40%。

1 相关工作

卷积神经网络随着深度学习的兴起，逐渐应用于遥感影像时间序列分类任务中。时间序列数据分类问题中，训练样本通常由一系列已标记的单序列时间序列样本构成，假设单变量时间序列X=[x1，x2，…，xT]是有序的一组实数值，其中X的长度为T。M维时间序列XM=[X1，X2，…，XM]是由M个不同的单变量时间序列构成的多元时间序列，其中Xi∈RT。数据集D={(X1，Y1)，(X2，Y2)，…，(XN，YN)}是(Xi，Yi)的集合，其中Xi可以是单变量或多元时间序列，Yi是其对应的one-hot编码标记向量。对于包含K个类别的数据集，时间序列Xi对应标记Yi∈{0，1}K，表示训练样本中有K个类别，Yi中仅有一个元素取1，取1 元素的索引为该时间序列的类别，其余元素均为0。多波段遥感影像提供了同一个位置上的多个不同光谱波段的强度，各个波段影像之间存在互补性和冗余性［18］。在遥感影像时间序列中，M维时间序列即是M个波段组成的多元时间序列，则数据集中地面特征可以表示为XM∈RN×T×M，其中N为像素数，T为时间序列长度即天数，M为时间序列维度即波段数量。本文中数据异常情况包括数据缺失和数据扭曲两种情况，其中数据缺失是指丢失部分像素，即N减少，以模拟遥感影像采集中数据量少的情况。数据扭曲则是针对时间序列长度，又分为压缩时间序列长度、拉伸时间序列长度和二者混合三种情况，即T变化，以模拟遥感影像采集中由于天气等原因，导致缺失某天或某段时间的数据等情况。

同时，地物的时间序列数据在遥感影像中呈点簇状分布，整体数据信息较为离散。在此情况下，LSTM 分类效果不理想［10，14］。文献［10-12］应用1D-CNN 算法可有效描述一维序列数据的特性，解决遥感影像时序分类问题。使用MCNN［13］对时序数据集进行分类。MCNN 模型包括3 个阶段：转换阶段、局部卷积阶段和全卷积阶段，其中转换阶段对输入时间序列应用各种转换，以应对现有时间序列分类方法中由于特征提取与分类过程分离所导致的无法提取不同时间尺度的不同特征的问题。MCNN 的局部卷积阶段，通过在多组时间序列上进行卷积，提取不同时间尺度序列的特征。不同的分支彼此独立，所有的输出将通过多个具有不同大小的最大池化层。全卷积阶段中将提取的所有特征连接起来，并通过多个跟着最大池化的卷积层、全连接层和softmax 层来生成最终的输出。MCNN 整体通过这个端到端的系统，反向传播所有的参数进行训练。该方法可以一定程度上应对数据缺失的问题，但该方法并未对数据的各个波段之间的关系进行考虑，无法应对数据扭曲，分类精确率较低。考虑到多模态时间序列的不同特征之间的假定独立性，多通道深度卷积神经网络（MCDNN）［16］在输入的每个维度上独立并行应用卷积。MCDNN 对传统的CNN 进行了改进，将多变量时间序列分解为单变量时间序列，即对每个Xi分别进行处理，然后在特征学习的最后连接一个多层感知机（Multi-Layer Perceptron，MLP）进行分类，但其无法应对数据缺失的情况。由于MCDNN 无法发挖掘出不同单变量之间的相互关系，TSCNN［17］联合训练多元时间序列进行特征提取。不同的单变量可能具有不同的价值，有的单变量区分度较大更有价值。传统的CNN通常使用交叉熵的softmax输出层，TSCNN的不同之处在于其使用了均方误差（Mean Squared Error，MSE）损失函数的Sigmoid输出层；并且在池化层部分使用平均池化层代替通常使用的最大池化层。在最后一个卷积层之后不再使用池化层。该方法考虑到了变量之间的关系，将整个数据作为一个整体进行训练，但不能学习不相关的时间序列之间的信息，无法应对数据扭曲的情况。通过分析各分类模型的优缺点，本文提出一种端到端的多模式与多单模式架构融合的网络。

2 端到端模式融合网络

端到端的多模式与多单模式的架构融合的网络的整体架构如图1 所示。该网络主要由两阶段构成：第一部分是自动编码阶段；第二部分为分类阶段。其中第一阶段又分为3 个部分：第1 个部分为多元时序模型，第2 个部分为单变量时间序列模型组合，第3个部分为像素坐标输入部分。

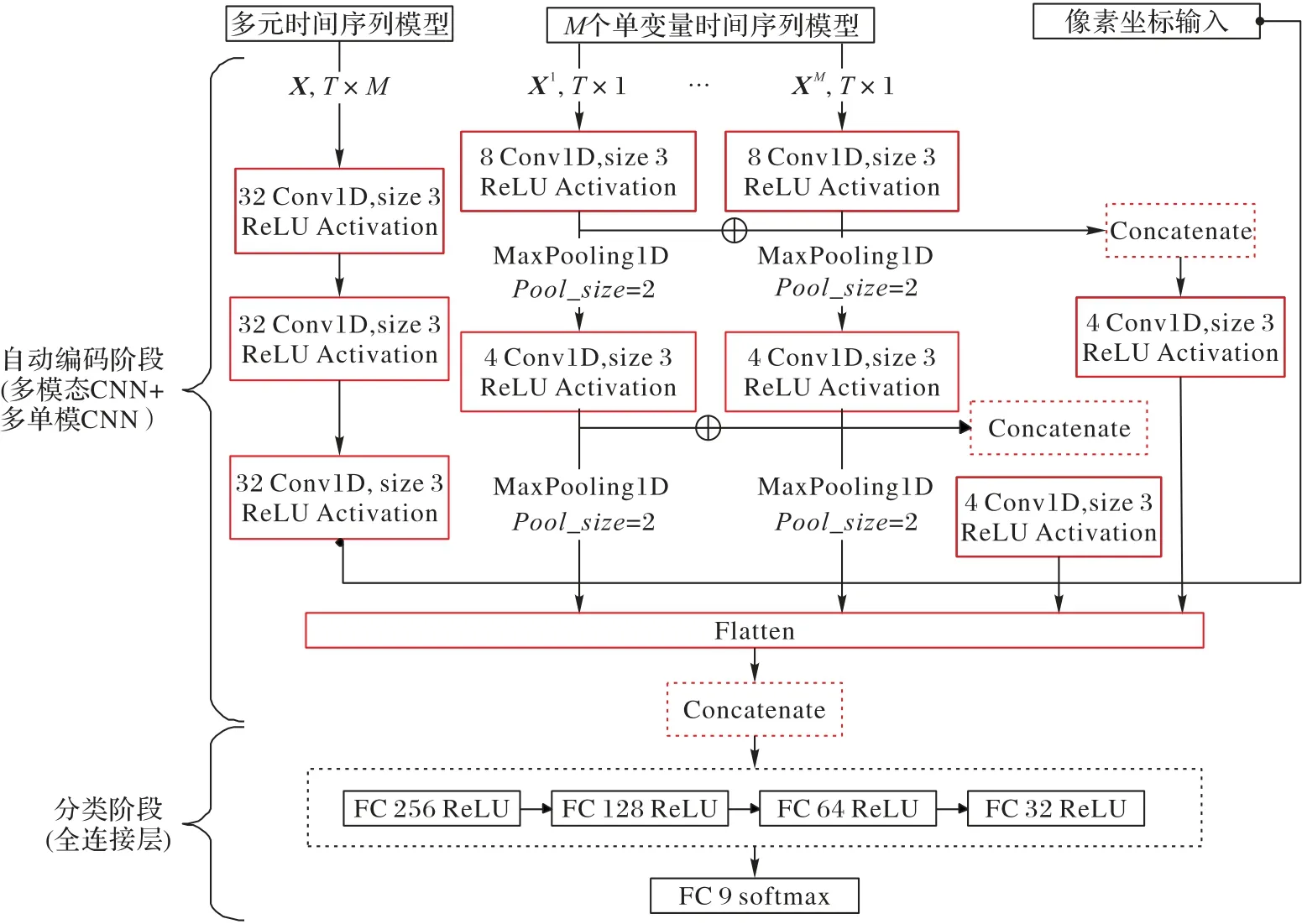
图1 端到端的多模式与多单模式架构融合的网络Fig.1 End-to-end multi-mode and multi-single-mode architecture fusion network

多元时序模型的输入为整个多维时序数据整体，这样可以很好地衡量多个单变量之间的关系。通过3 个卷积层进行特征抽取，并且进行扁平化，输出整体多维时间序列数据的特征。单变量时间序列组合则是对各个单变量时间序列单独进行多尺度的提取，包括两个带着最大池化层的卷积层，其中各个单变量在第一层卷积之后进行连接，并再次卷积。第二层卷积之后的特征图也进行连接，再进行卷积与扁平化。该特征与单个通道及第一层后的连接特征图共同进行最大池化与扁平化后连接，送入自动编码阶段的最后一层，输出一系列单变量时间序列的特征。像素坐标输入部分则将经过预处理的像素坐标，按比例缩放后直接送入最后一层。自编码阶段最后一层连接以上3 个部分的输出，将其输入分类阶段。总的来说，待分类的时间序列数据会以整体和单个变量的形式分别输入网络，经过不同的卷积神经网络，得到所有的特征集合，其中包括不同尺度的特征，最后与像素坐标一同连接，得到时间序列特征。

分类阶段则是通过全连接层的叠加对自动编码阶段得到的时间序列特征进行分类。将5 个全连接层间学习到的时序特征映射到样本标记空间。并在第2 个全连接层与第3 个全连接层使用Dropout，使得神经元与其他随机挑选神经元共同工作，来避免模型过拟合，增加了泛化能力。最后一层的全连接层通过softmax 获得分类概率，对像素进行分类，得到地物的类别标签。最终整个网络以时序特征的分类损失为整体的网络损失进行反向传播，得到端到端的时间序列分类模型。网络的整体学习过程将在下文进行具体的介绍。

由于时序分类网络对待时序数据角度不同，一个假定时间序列不相关，可以应对数据缺失情况；另一个则认为这些时间序列是一整个实体，可以应对数据扭曲的情况。本文提出的端到端的多模式与多单模式架构融合的网络则可以将二者结合起来，以解决遥感影像时间序列数据异常的问题。

3 网络结构

时间序列分类问题中，训练样本通常由一系列已标记的单变量时间序列样本构成，假设单变量时间序列X=[x1，x2，…，xT]是有序的一组实数值，其中X的长度T。M维时间序列XM=[X1，X2，…，XM]是由M个不同的单变量时间序列构成的多元时间序列，其中Xi∈RT。

在整个体系结构中的自动编码阶段，使用了3 种不同的模型，输入数据首先被用来训练一个多元时序模型卷积神经网络，将M维遥感影像时间序列作为一个整体进行处理，输入时序数据的维度是T×M，即对XM整体进行卷积。通过连续三层卷积，其中每层包括为32个尺寸为3×3的卷积核，以获得整体的时间序列特征。

3.1 单变量时间序列模型组合

各类地物对应的遥感影像时间序列变化不一，单靠一种波段很难进行分类，且各个波段信息之间存在一定的冗余。因此需要对多个单变量进行结合。单变量时间序列模型对M维时间序列数据XM=[X1，X2，…，XM]中每一维单独进行处理，即对X=[x1，x2，…，xT]进行处理；并且将M个处理后的数据在不同的层级进行连接以获取不同尺度的时间序列，如图2 所示。每个波段的时间序列被输入到卷积层中，第一个卷积层包括8 个尺寸为3×3 的卷积核。每个波段的第二个卷积层包括4个尺寸为3×3的卷积核。分别在第一个、第二个卷积层后对得到的特征图进行连接，对第一层卷积后的连接特征图使用8个尺寸10×10的卷积核进行卷积并卷积，对第二层卷积后的连接特征图使用4个尺寸为10×10的卷积和进行卷积，并且将得到的结果扁平化与每个通道卷积后的结果扁平化后连接。这样既结合了单变量进行训练，又使用了不同尺度的特征进行采样，丰富了卷积网络所提取到的特征图，有利于解决数据扭曲的问题。

自动编码阶段的第3 部分模型负责处理像素的坐标，预处理按比例缩放的像素坐标并与另外两个模型的结果连接，交给全连接层一起处理。

图2 多单模式的架构Fig.2 Multi-single-mode architecture

3.2 分类阶段

本阶段使用具有256 个神经元的全连接层，激活函数为线性整流函数（Rectified Linear Unit，ReLU）。数据经过128个神经元的全连接层，并且以0.3 的概率神经元不工作，再经过64个神经元的全连接层，以0.3的概率神经元不工作，避免过拟合。最后通过32个神经元的全连接层，连接到softmax层对像素进行分类。分类阶段通过在128 个神经元、64 个神经元和32个神经元这3个全连接层之间增加Dropout层，来避免过拟合，增加模型的泛化能力。

模型使用自适应矩估计Adam 优化器，学习率为0.001，每个批次的大小Batch size 的大小为256，共计50 个Epoch。动态调整学习率，每次调整时学习率变为原学习率的0.2 倍。经过3 个Epoch 训练后，模型性能不再提升，学习率减小。学习率的下限为0.000 01。

4 实验与分析

4.1 实验环境和实验设置

采用TensorFlow 2.2.0 开源框架，搭建在操作系统为Ubuntu16.04，Python 版本为3.6 的平台上，平台显卡型号为GeForce GTX TITAN XP。本文设置模型学习率（Learning Rate，LR）为0.001，每个批次的大小Batch size 为256，训练数据集次数Epochs为100。对比模型的参数如下。

1D-CNN：LR=0.01，Batch size=256，Epochs=100，降采样因子为2，即时间序列下采样为原先的二分之一。滑动平均窗口大小为4，即时间序列的值为本值与该位置前两个和后两个的平均值。

4.2 实验数据和数据准备

所使用的数据集是来自于TiSeLaC（The time Series Land Cover classification challenge）［15］，2014 年在留尼汪岛的23 幅Landsat 8 影像生成的时间序列数据集。留尼汪岛影像如图3（a）所示，土地覆盖类型如图3（b）所示。

图3 留尼汪岛遥感影像Fig.3 Remote sensing images of Reunion Island

该遥感影像级别为2A，尺寸为2 866 像素×2 633 像素，地面分辨率30 m。在每个时间戳，每个像素有10 个特征值，包括7 个表面反射率（海岸波段ultra blue、蓝波段blue、绿波段green、红波段red、近红外波段NIR、短波红外1 SWIR1 和短波红外2 SWIR2）和3 个辐射指数：NDVI、归一化水指数（Normalized Difference Water Index，NDWI）和亮度指数（Brightness Index，BI）。而数据集的土地覆盖类型数据，即像素类别标签则是由2012 年Corine 土地覆盖地图［19］和2014 年Graphical Land Parcel 注册信息联合标注而得，以保证其真实可靠。训练集包括81 714个像素，测试集为17 973个像素，共计9个类别，如表1所示。

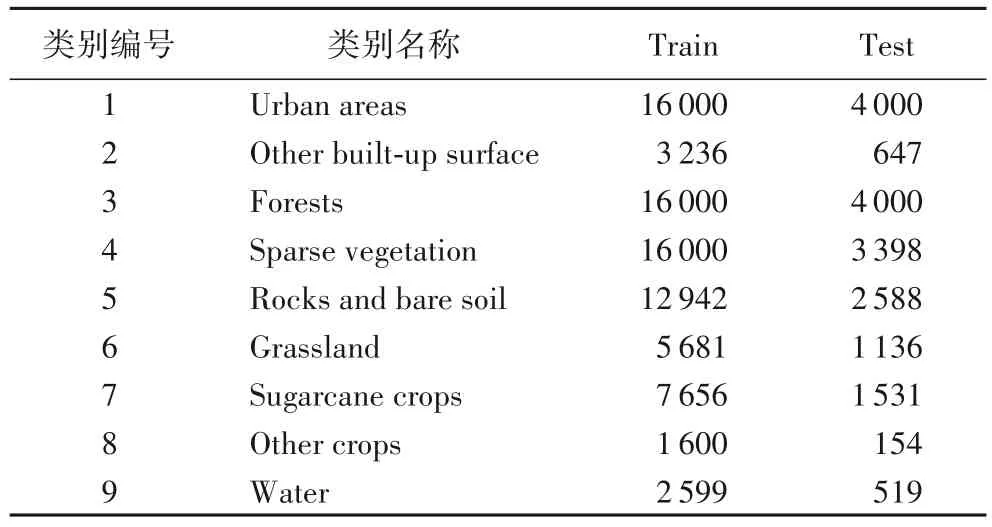
表1 数据集类别分布Tab.1 Dataset class distribution

数据集中地面特征可以表示为XM∈RN×T×M，其中N=81 714 个像素，T=23 d，M=10 为特征数量即波段数与辐射指数数量之和。

本文通过数据处理来模拟数据异常情况。首先是数据缺失情况，即存在部分像素点缺失。本文采用随机删减策略进行模拟，即通过一定概率随机删除部分像素点，并最终只保留固定数量的像素点进行数据训练。其次，针对数据扭曲，包括时序数据压缩操作、拉伸操作和两者混合操作。其中：图4（a）表示原始时间序列；压缩操作表现为基于时序数据按照固定步长进行抽取，如图4（b）所示；拉伸操作表现为对特定时序区间进行线性插值进行数据填充，如图4（c）所示。

图4 时间序列数据操作Fig.4 Operations for time-series data

4.3 评价指标

为客观评价卷积神经网络的分类性能，本文使用精确率（Precision）、召回率（Recall）和F1值作为评价指标。其中真阳（True Positive，TP）、假阳（False Positive，FP）、假阴（False Negative，FN）和真阴（True Negative，TN）分别表示：

TP：实际为正、预测为正的样本数量；

FP：实际为负、预测为正的样本数量；

FN：实际为正、预测为负的样本数量；

TN：实际为负、预测为负的样本数量。

1）精确率。

精确率指模型预测为正的样本中实际也为正的样本，占被预测为正的样本的比例，即：

精确率体现了模型对负样本的区分能力，精确率越高，模型对负样本的区分能力越强。

2）召回率。

召回率指实际为正的样本中，被预测为正的样本，占实际为正的样本的比例，即：

召回率体现了模型对正样本的识别能力，召回率越高，模型对正样本的识别能力越强。

3）F1值。

F1 值是评价卷积神经网络性能的常见指标。F1 值通过精确率和召回率计算，公式如下：

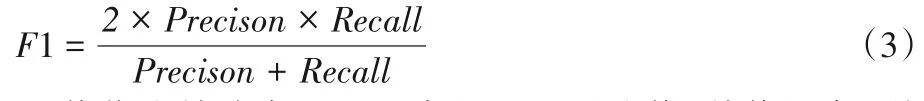
F1 值作为精确率和召回率的调和平均值，其值越高，说明模型越稳健。

4.4 实验结果分析

本文比较了不同模型在数据缺失与数据扭曲情况下对时序数据分类性能的影响。以23 d时间序列数据为原始数据集，1D-CNN、MCDNN、TSCNN、LSTM 和端到端的多模式与多单模式架构融合的网络这五种时序分类网络得到的结果如表2 所示，F1 值分别为88.47%、86.34%、88.68%、92.41% 和93.40%。其中：1D-CNN 采用Adam 优化器，初始学习率为0.001；MCDNN 采用随机梯度下降策略（Stochastic Gradient Descent，SGD）与0.01的学习率；TSCNN采用学习率不变化的Adam优化器，学习率为0.001。由于LSTM形式的深层递归神经网络在这种像素较少的情况下，训练效果不佳［14］。本文所使用的LSTM网络为借助LSTM结构对端到端的多模式与多单模式架构融合的网络进行结合，以提升LSTM网络性能。通过将本文网络中的多元时序模型，替换为输出维度为512 的LSTM网络，对时序数据进行整体特征提取，再结合网络中的多单变量网络与像素坐标，最后在分类阶段对数据进行分类。

在这种原始情况下，五种时序分类网络的精确率和召回率相仿，说明其对正负样本的识别能力都很强。从中可以看出，端到端的多模式与多单模式架构融合的网络对时序数据分类性能最好，精确度达到了93.5%。而数据缺失的情况，即以80%的概率删除训练集中的像素点，剩余16 343个像素点。当训练数据变少时，端到端的多模式与多单模式架构融合的网络的F1值仍然最优。同时，MCDNN 在此时受影响较大，精确度只有73.31%，且各个网络的F1 值均有所降低，说明训练数据减少会影响分类效果。其中对TSCNN 影响最小，精度下降约4%。端到端的多模式与多单模式架构融合的网络的前后变化较小，说明数据量变小对其影响较小。端到端的多模式与多单模式架构融合的网络由于使用三种不同模型来对原始时序数据进行分类，故而较为分类效果稳定，可以应对数据缺失的问题。

为模拟数据扭曲的情况，本文压缩部分时序数据同时拼接剩余数据，共剩余6 d时序数据。此时在数据缺失情况下表现优异的TSCNN，分类精度却下降最大，说明在时间维度较小的数据集中，将所有波段特征作为一个整体，区分度较低。本文模型性能受影响较小，仍能保持92.65%的F1值，分类性能优于其他模型。为模拟数据采集较少的情况，即只有15 d时序数据的情况下，需要考虑对数据进行填充，通过线性插值的方法对其进行填充，将数据填充回原数据集的大小进行训练。在这种情况下，得到的分类结果与原始数据的分类结果基本一致，说明这类时序数据中线性插值的方法是有效的，可以提高训练数据较少时的分类精度。而在数据拉伸的情况下，本文通过对相邻时间区间的数据进行之间线性插值，获得共40 d 时序数据，并对此进行分类。在这种情况下由于1D-CNN 和MCDNN网络结构较为简单，对遥感影像时序数据描述能力较弱，可能会产生过拟合现象，导致分类效果变差F1值降低；但TSCNN和本文提出的端到端的多模式与多单模式架构融合的网络结构考虑到了将多维特征作为整体学习，模型复杂描述能力强，在数据较为复杂的情况下，仍能有效表示时序数据。可以考虑扩充时间维度来增加数据，提升模型分类能力。

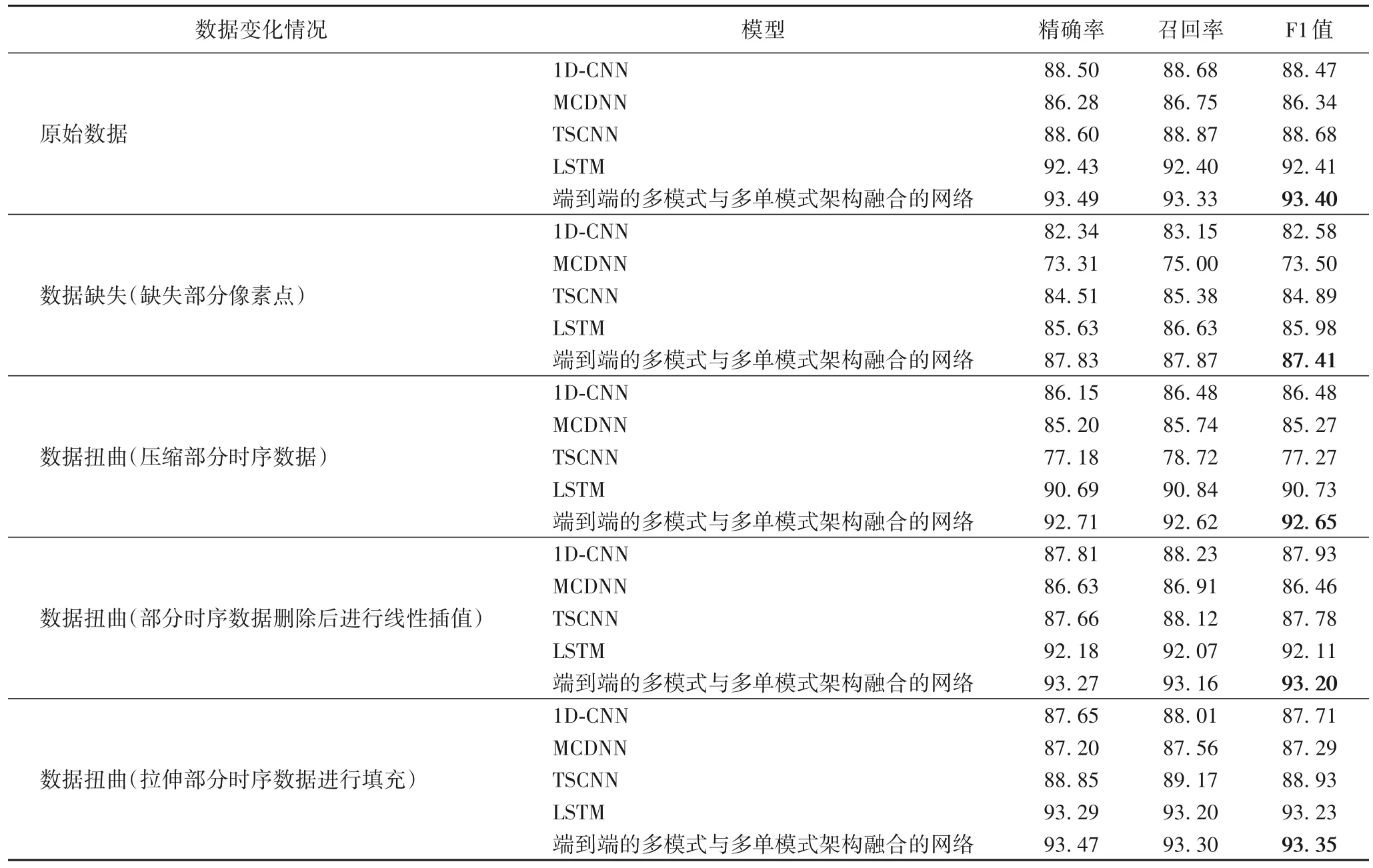
表2 时序数据分类结果 单位：%Tab.2 Results of time-series data classification unit：%

综合考虑各种情况，端到端的多模式与多单模式架构融合的网络的分类结果均好于其他模型，说明了其能应对数据异常的问题。

在原始情况下，五种时序分类网络的时间性能如表3 所示。由于1D-CNN 需要对原始时间序列数据进行转换，对于单一时间序列输入进行降采样和滑动平均等变化，所以训练用时最长，性能最差，其余模型时间性能接近。MCDNN 用时最短，单个Epoch 用时为2.006 s，效率最高。其次是TSCNN。本文模型单Epoch 用时与LSTM 基本一致，分别为5.016 s 和5.018 s。综合精度与时间性能，本文模型效果更好。

表3 时序数据分类用时Tab.3 Time consumption of time-series data classification

本文网络在9个地物类别的分类效果有所不同，图5展示了在9 类不同地物分类任务上的混淆矩阵。从图中可以看出，9 个类别都可以被区分开，其中其他作物类相对区分度较低，其原因主要是其在训练样本中所占数量较少，训练较为不充分。城市地区与其他建筑物由于光谱反射率较为接近，也存在一定的误分现象。

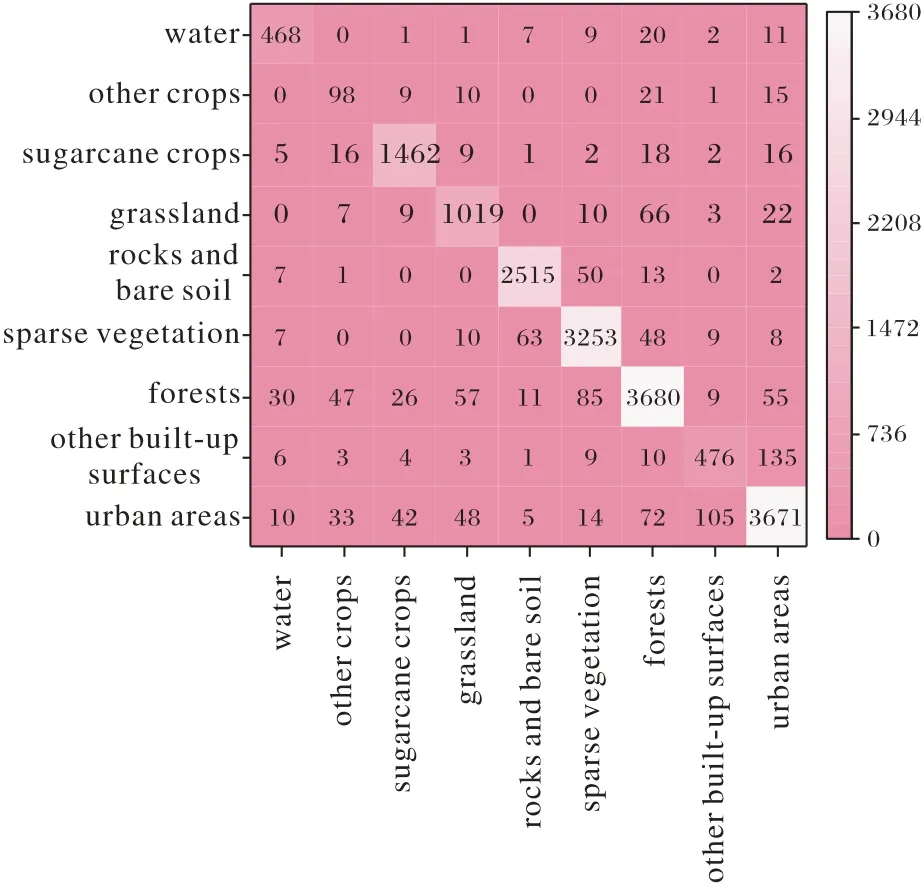
图5 混淆矩阵Fig.5 Confusion matrix

5 结语

遥感影像时间序列分类在遥感影像分类中十分重要，本文提出了一种端到端的多模式与多单模式架构融合的网络，可以通过结合多元时序模型和多尺度单变量模型进行特征提取，与像素坐标汇总后进行分类，并通过使用公开遥感影像时序数据集对1D-CNN、MCDNN、TSCNN、LSTM 和本文模型进行验证，实验表明：在数据异常的情况下，本文模型仍然保持了分类精度优于其他模型，且F1 值变化较小，说明了本文模型具有鲁棒性。该模型在解决时序分类的问题上，尚有进一步研究的空间，后续工作将使用模型初始化方法提高模型分类精度，以及研究更极端条件对模型的影响。