多段索异形塔斜拉桥施工阶段索力计算

陈璐，陈小佳

(1.西南交通大学 桥梁工程系,四川 成都 610031； 2.武汉理工大学 交通学院)

1 前言

桥梁除满足日常交通需求外，发挥一定城市景观效应已成为设计者、管理者的共识，即建筑美学成为重要设计与评价指标。斜拉桥上部结构主要由索塔、主梁和斜拉索组成，造型优美，尤其多段索异形塔斜拉桥突破传统斜拉桥构造形式，其时尚感、轻巧感符合人们对斜拉桥的审美，在城市桥梁建设中逐步得到采用。这种桥梁形式具有多个桥塔以及由多段索组成的复杂索面布置，除了桥塔和桥面主梁之间的一般斜拉索(后简称为塔梁索)外，还包括桥塔之间的斜拉索(后简称为塔间索)。该文暂称该类桥型为多段索异形塔斜拉桥。上述斜拉桥类型不同于一般独塔斜拉桥，拉索由塔间索和塔梁索组成。其桥塔刚度受塔间索索力量值的影响较大，主梁、桥塔的刚度及拉索索力分布又决定了主梁和桥塔的偏位，而偏位情况又反过来影响塔间索、塔梁索索力，进而影响桥塔刚度。

国内外学者对斜拉桥索力计算方法进行了大量研究，目前常规斜拉桥索力计算方法主要有倒拆法、正装迭代法、倒拆-正装迭代法、无应力状态法等。其中，正装迭代法、倒拆法、正装-倒拆迭代法均属于“与建设过程相关”的施工阶段索力计算方法，即结构最终成桥状态的内力与位移均与结构形成过程相关。实际施工中，一旦发生如施工工序改变、临时外荷载出现和温度变化等工况，按照原定斜拉索张拉力施工得到的成桥状态必然会发生改变，必须对后续施工阶段的拉索张拉力进行调整。然而，由于上述所提到的该类斜拉桥特点，若采用这3种方法，寻找和控制“中间施工过程”的难度将急剧增大，索力调整计算十分繁琐。无应力状态控制法属于“与建设过程无关”的施工阶段索力计算方法。其基本原理为：无应力状态量是结构单元的固有特性值，如果确定了结构两个状态的无应力状态量，也就将两个状态的内在联系进行了确定，因此只要能够保证结构构件单元的无应力状态量，外荷载、支座布置与规定的合理成桥状态一致，则结构最终成桥状态的结构内力、位移将与合理成桥状态吻合。

斜拉索无应力长度为斜拉结构受到轴向力变形后的几何长度与斜拉索单元因轴向力而产生的伸长值之间的差值。图1为斜拉索单元无应力索长计算图示，变形前两端节点坐标分别为(xa,ya)和(xb,yb)；拉索受轴向力作用单元产生位移，两端节点的位移分别表示为(wa,va)和(wb,vb)。故结构受载后两端节点坐标为(xa+wa,ya+va)和(xb+wb,yb+vb)。为简化处理，忽略斜拉结构因自重产生的垂度等非线性因素的影响，拉索单元受到轴向力后的几何长度，因轴向力而产生的弹性变形以及单元的无应力长度分别根据式(1)～(3)确定。

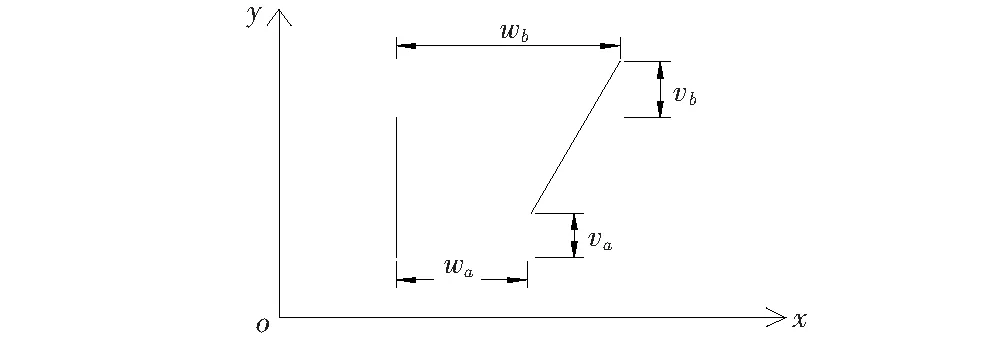
图1 无应力索长计算图示

L=

(1)

(2)

L0=L-ΔL

(3)

式中：F为轴向力；E为弹性模量；A为斜拉索单元截面面积。

无应力状态控制法在单塔双跨和双塔三跨等斜拉桥施工监控中取得了良好的效果，然而，对多段索异形塔斜拉桥这种施工工艺尤其复杂的桥型而言，运用无应力状态控制理论进行塔间索、塔梁索各施工阶段索力计算及调整的研究较为缺乏。

鉴于多段索异形塔斜拉桥工艺复杂，施工阶段繁多，该文结合无应力状态法，除了确定斜拉桥合理成桥状态作为考虑分阶段施工的最终目标状态外，结合桥梁实际施工过程，增设部分中间施工控制状态为合理中间施工状态，求解对应状态结构单元无应力状态量来指导分阶段正装模型的建立，从而得到各施工阶段的拉索张拉力。其计算流程可归纳为：① 确定斜拉桥的合理成桥状态，作为指导分阶段施工的最终目标状态；② 拟定部分中间施工状态作为指导斜拉桥中间施工的目标状态；③ 求解合理成桥状态及中间施工控制状态下结构单元的无应力状态量；④ 遵循实际的建造过程，合理划分施工阶段，以单元无应力状态量贯穿施工全过程，指导分阶段正装模型的建立，同时根据锚头拔出量辅以桥梁施工监控；⑤ 将一次成桥模型与无应力状态法指导施工正装的分阶段模型所得成桥状态进行比较，并考虑实际施工中的调索问题。具体计算流程如图2所示。

2 项目概要及模型建立

湖北随州氵厥水一桥为多段索异形塔斜拉桥，如图3所示，组合式钢拱塔包含两侧的2个主塔与中间1个副塔，多段索由主、副塔之间的塔间索及主塔、主梁间的塔梁索组成，全桥共16对塔梁索和16对塔间索。

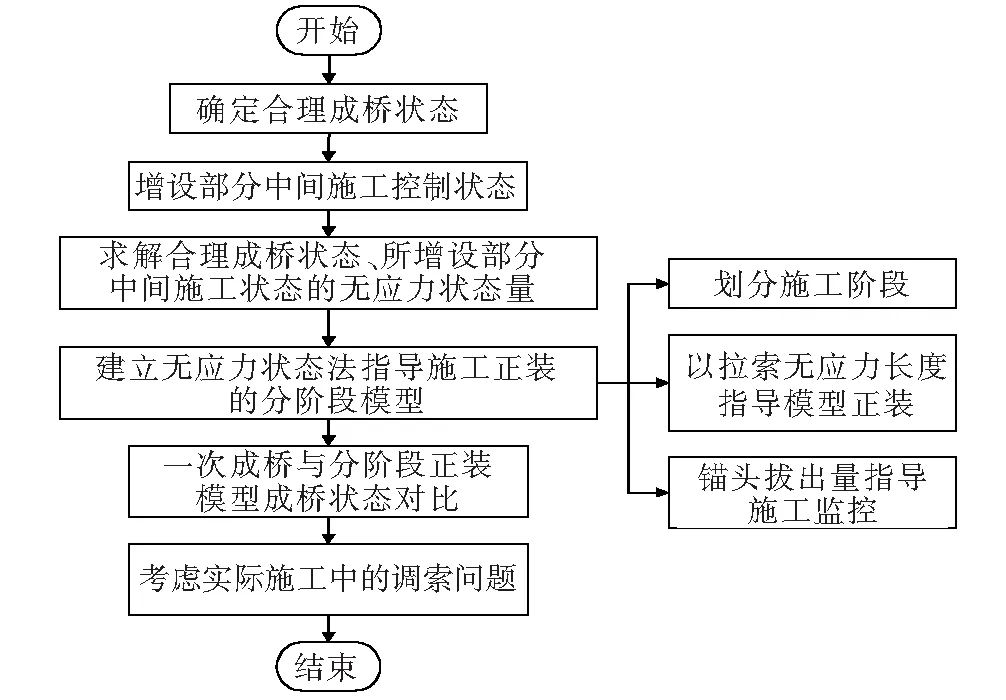
图2 结合无应力状态法计算施工阶段索力流程图

图3 氵厥水一桥

塔间索由下至上依次编号为T1、T2、…、T8，塔梁(斜拉)索由桥塔处至两端依次编号为S1、S2、…、S8，主桥立面布置如图4所示。

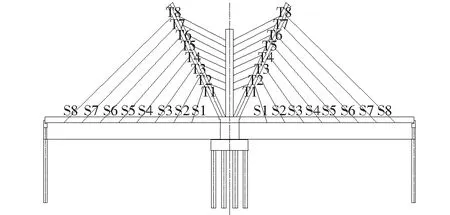
图4 主桥立面布置图

由于氵厥水一桥斜拉索由多段索组成，张拉过程复杂，现对其进行说明。实际施工中，斜拉索张拉分2次，包括初张拉与终张拉，而初张拉和终张拉又各分3级进行，即采用“三拉到位”。初张拉从塔间索开始按T1～T8的顺序张拉，目的是使桥塔在受力安全的情况下脱离桥塔临时支架。塔间索初张拉完后，桥塔完成脱架，将塔梁(斜拉)索挂设完成，进行塔间索T8～T1的终张拉。

塔间索终张拉完毕，按S1～S8的顺序进行塔梁(斜拉)索的初张拉。类似于塔间索，塔梁(斜拉)索初张拉的目的是使主梁在受力安全的条件下，脱离主梁临时支架。主梁脱架结束，二期恒载施工完成后，进行塔梁(斜拉)索的终张拉。终张拉时，塔梁(斜拉)索仍按S1～S8的顺序进行。

采用Midas/Civil建立了该桥的空间有限元模型(图5)，共包含232个节点，374个单元。主梁、拉索截面的材料参数如表1所示，与实际结构一致。有限元模型中，采用梁单元模拟钢箱梁和桥塔结构，采用弹性连接模拟塔梁分离。为实现无应力索长指导模型正装，结合索张拉具体施工情况，对每根索设置多个同节点索单元。按照分级张拉的需要，分别激活具有初拉力荷载或无应力长度属性的索单元。根据无应力状态法理论，一组无应力索长值的改变必然唯一对应着索力的改变，因此利用无应力状态法可以快速地求解出拉索各阶段的张拉力，同时可通过锚头的拔出量辅以斜拉桥的施工监控。

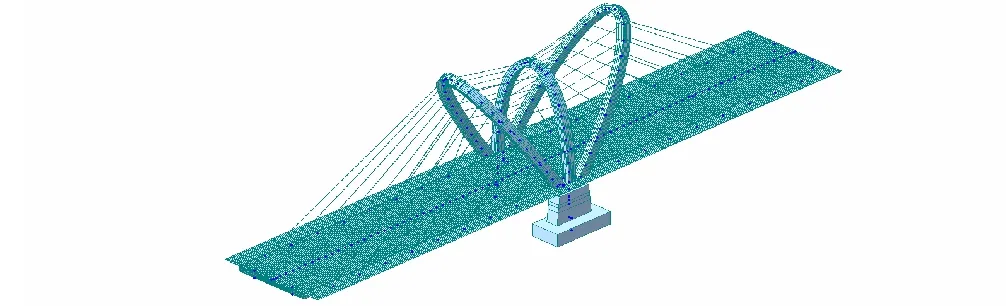
图5 桥梁有限元模型图

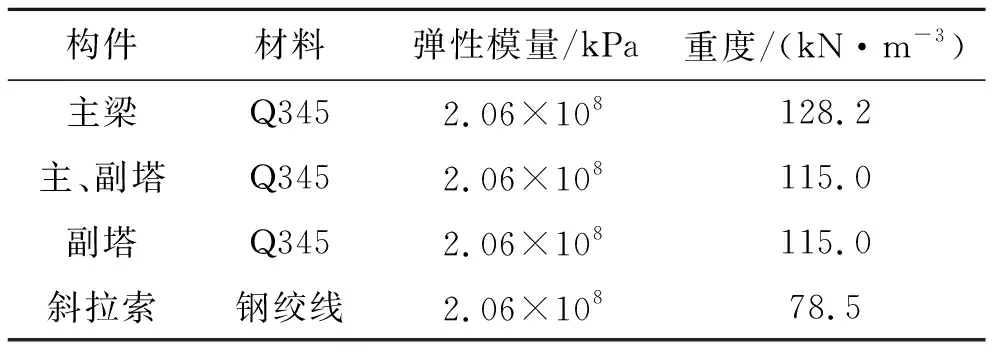
表1 主要截面参数

3 成桥及施工阶段索力计算

3.1 合理成桥状态确定

在建立Midas三维有限元模型的基础上，基于索力和主梁内力分布均匀、主塔和主梁预偏合理等原则,该文采用刚性支承连续梁法并结合未知荷载系数法确定桥梁的合理成桥状态，如图6所示。

3.2 中间施工控制状态的拟定

多段索异形塔斜拉桥由于索分段张拉，施工控制存在明显的阶段性。氵厥水一桥主、副塔及主梁施工采用了支架拼装施工方式，主、副塔及主梁通过索的初张拉完成脱架过程，其中主、副塔脱架通过塔间索初张拉完成；主梁脱架则在塔间索完成张拉后通过塔梁索初张拉来实现，两个工况均作为施工中间控制状态，以塔间索和塔梁索的初张力为控制参数。各初张力以脱离支架、索不出现负索力及塔、梁受力均衡为原则，确定的塔梁索和塔间索初张拉索力值如表2所示。

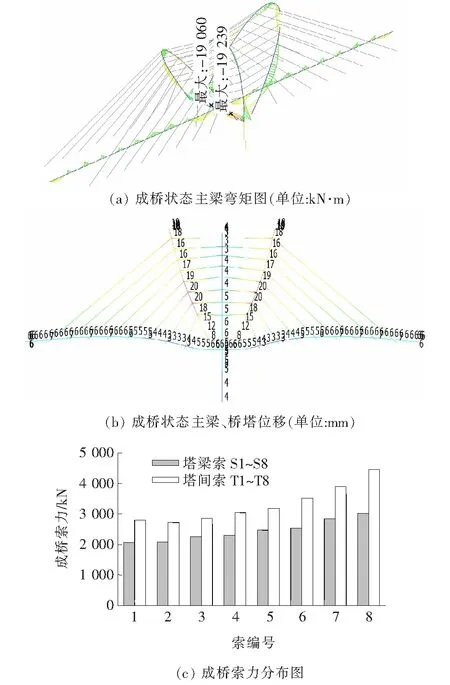
图6 成桥阶段状态图

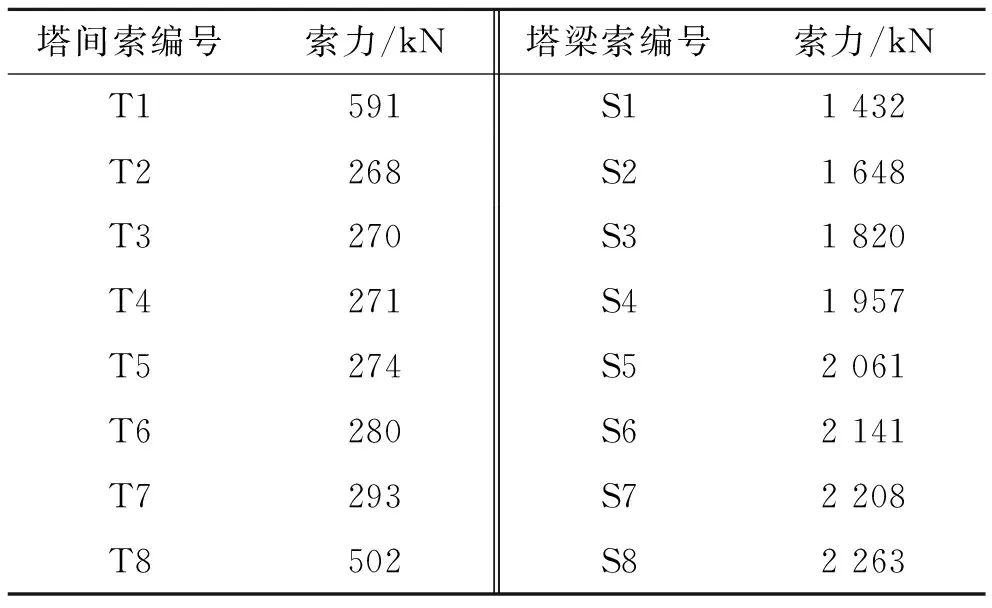
表2 各斜拉索初张拉索力值

3.3 合理成桥状态及中间施工控制状态无应力长度求解

在得到合理成桥状态控制索力后，各塔间索、塔梁索在成桥状态下的无应力长度可以按照一次成桥模型较方便地计算，即建立一次加载成桥模型，将成桥控制索力以初拉力形式赋予索单元便可计算合理成桥状态下各索的无应力索长。

同上述做法，分别建立塔间索、塔梁索初张拉施工阶段的一次落架模型，以初拉力形式赋予塔间索和塔梁索脱架控制索力，求得两个中间施工控制状态的无应力长度，结果如表3、4所示。

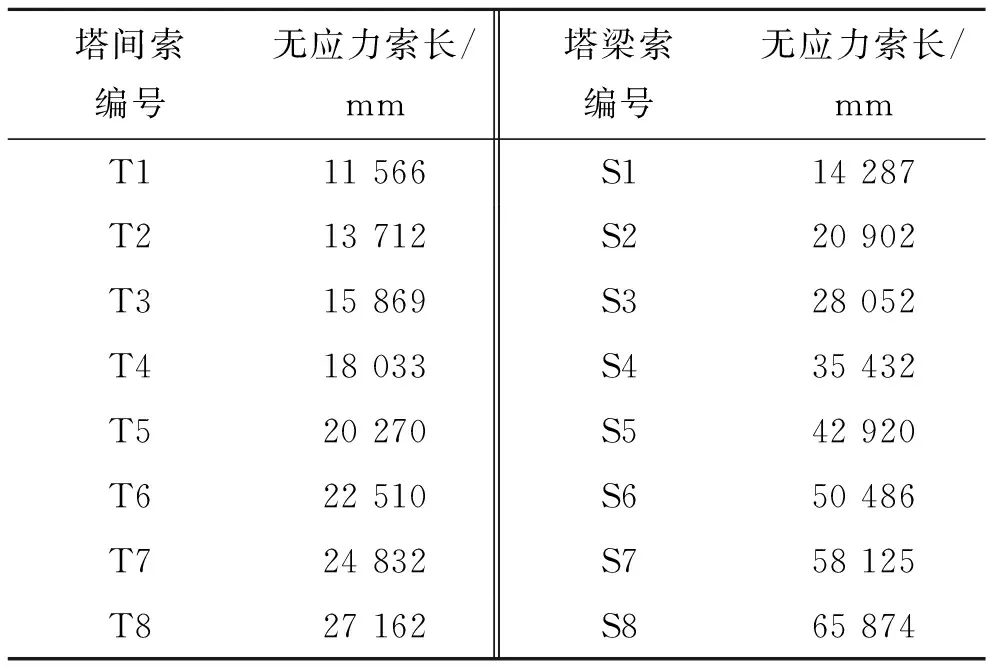
表3 斜拉索初张拉时无应力索长值

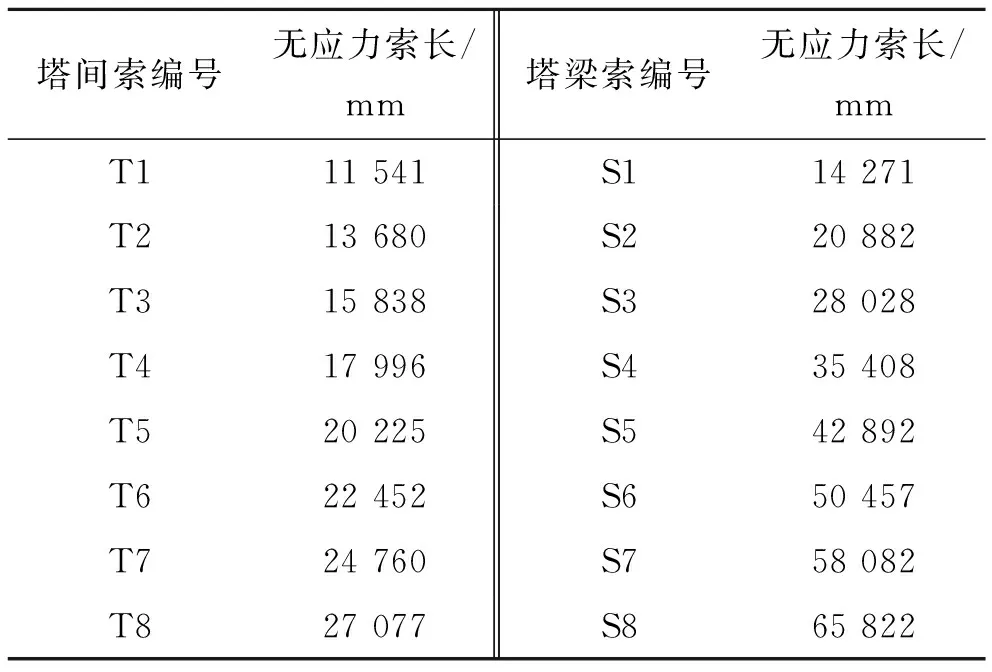
表4 斜拉索成桥无应力索长值

3.4 无应力状态量应用于施工过程控制

据前所述施工流程及张拉方式，建立分阶段的施工正装模型，合计共104个施工阶段。

在各张拉工况中，以无应力长度逐步激活各索单元，即可相应得到各索施工的张拉控制索力。按照实际施工工序，塔间索和塔梁索均按照3级：即控制索力的50%、80%和100%进行张拉施工。3级张拉中对各索索力的控制，前2级张拉采用索力进行控制，第3级张拉采用无应力索长控制。模型计算中只需要将各索单元的无应力索长调整至对应阶段合理目标状态所对应的无应力索长即可。尽管各组拉索张拉完成后，后续阶段的施工会使多段索包含的各组斜拉索内力重分布，但根据无应力状态法理论，只要能确保索力的变化幅度在安全范围内，拉索的无应力索长值不变，则分阶段施工的最终成桥状态就能够和一次落架的成桥状态吻合。用于指导张拉施工及监控的锚头拔出量如表5所示。

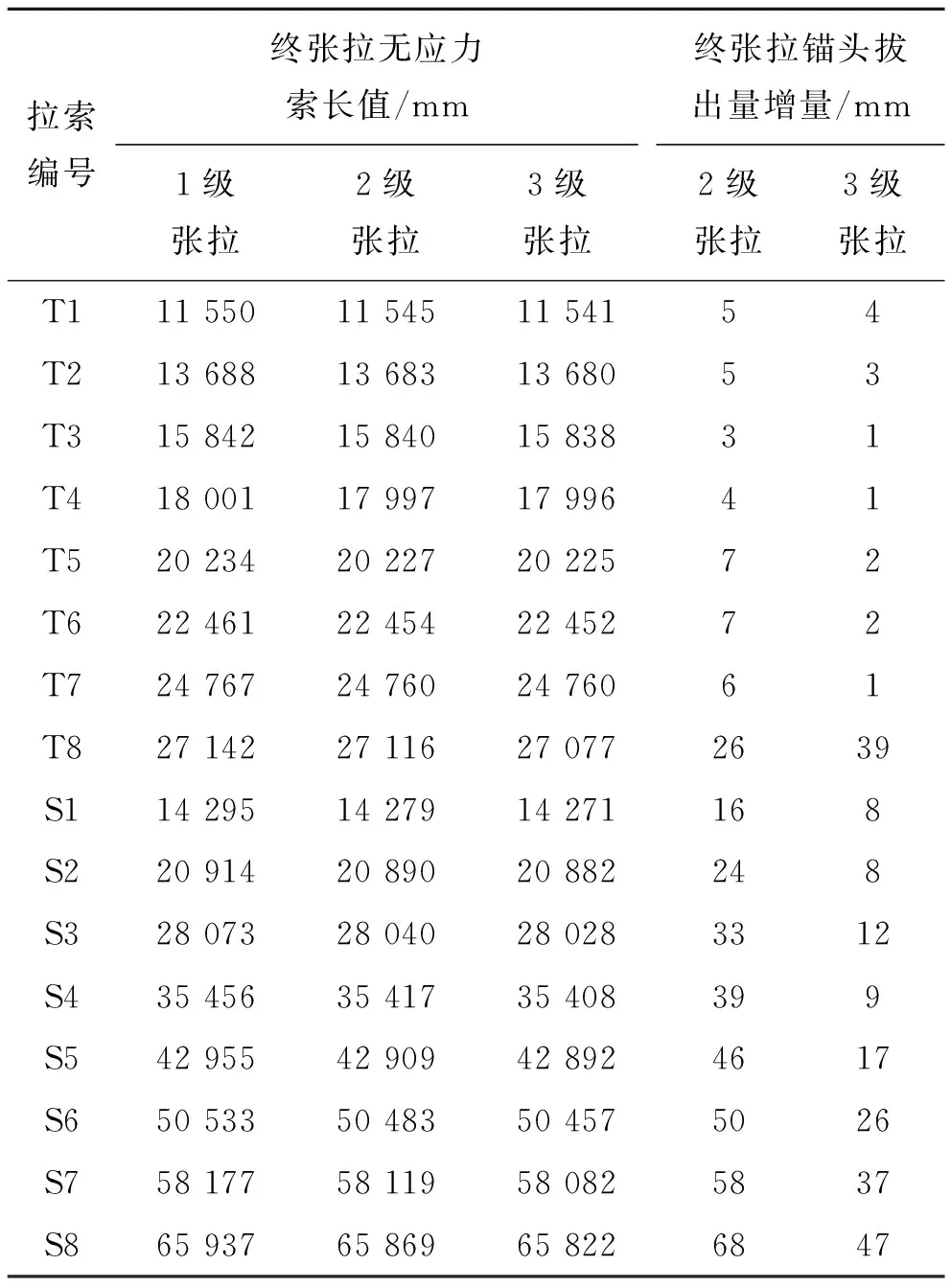
表5 斜拉索终张拉无应力索长值及拔出量

斜拉索索力和结构的位移会随着外荷载、结构体系的改变和斜拉索索力的张拉调整而发生改变，而斜拉索的无应力长度只有在自身张拉时，斜拉索锚固位置通过拔出或放回索长(锚固螺母移动)才发生改变。以塔梁索S8为例，终1级张拉时，对应单元的无应力索长值为65 937 mm，终2级张拉时，对应单元的无应力索长值为65 869 mm，终3级张拉时，对应单元的无应力索长值为65 822 mm。故在第二次和终张拉时可利用锚头拔出量进行斜拉桥施工监控。终2级张拉时，仍提供施工单位张拉力，同时辅以锚头拔出量：65 937-65 869=68 mm作为参考；终3级张拉时，以锚头拔出量：65 869-65 822=47 mm进行控制。

4 基于无应力状态法的计算分析

4.1 分阶段成桥与一次成桥模型成桥索力对比

根据无应力状态法理论，要实现分阶段成桥结构最终状态与一次成桥形成的合理成桥目标状态一致，应保证在分阶段施工过程中各构件的无应力状态量与一次成桥的目标状态相同。为了验证按照各阶段无应力长度计算的准确性，该文将无应力长度分阶段正装模型与一次落架模型进行了比较。两种模型成桥索力对比如表6所示。

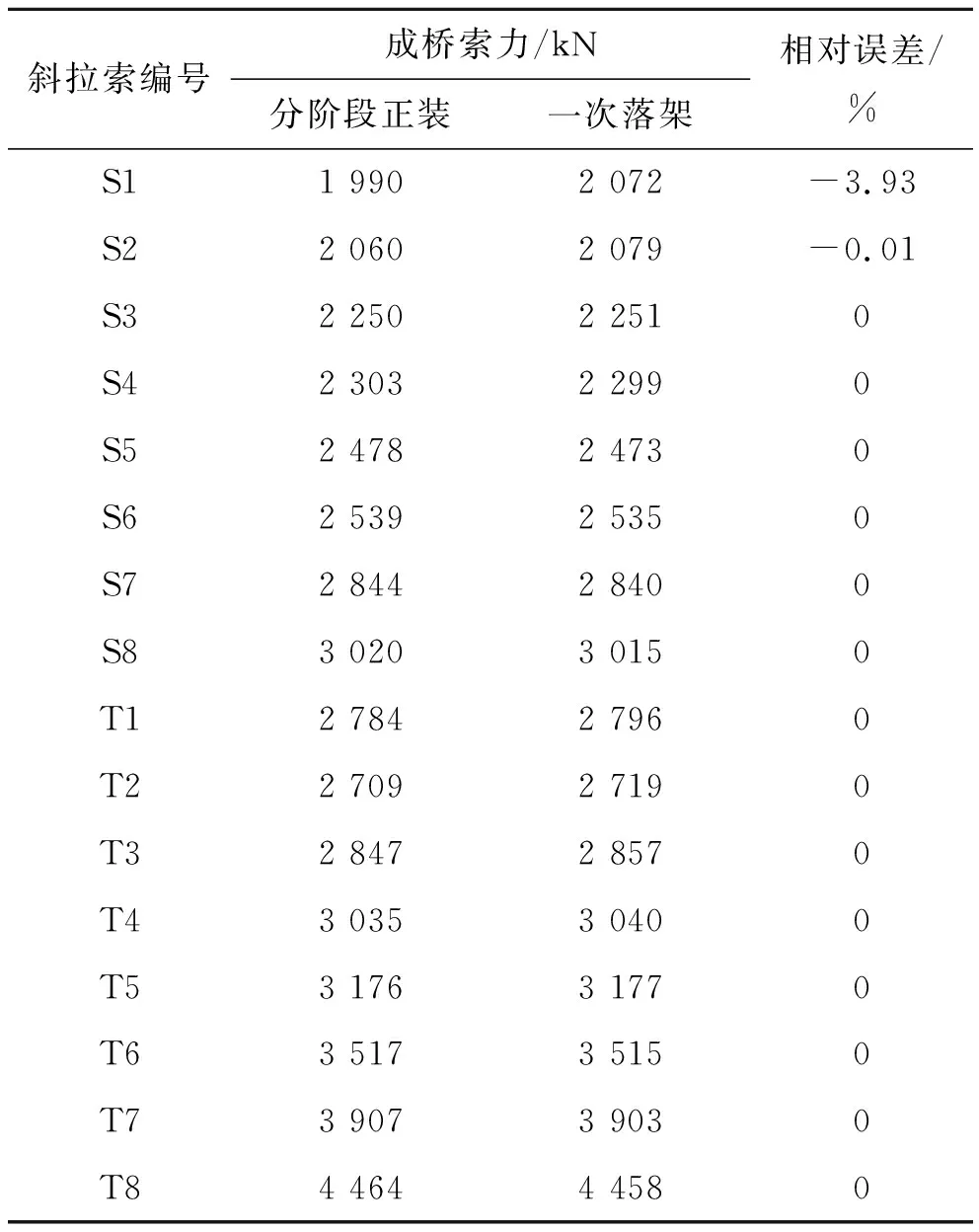
表6 成桥索力对比

由表6可以看出：两者的索力吻合良好。除塔梁索S1因索长较短且有弹性支承而误差相对较大(小于4%)以外，其余拉索成桥索力的误差均小于0.01%。表明采用无应力状态控制法指导多段索异形塔斜拉桥施工正装能快速求解各施工阶段拉索的张拉力。

4.2 施工工序变更后与原正装模型成桥索力对比

斜拉桥施工过程中，由于施工环境复杂，施工工序常常发生变更，不可预估的临时外荷载无法避免。无应力状态法认为，拉索的索力是随外荷载、施工顺序的改变而改变的敏感量值，但只要能保证无应力状态量不发生改变，成桥状态就能吻合。现结合氵厥水一桥工程实例讨论桥面上出现临时外荷载和拉索张拉顺序变更两种情况下，采用无应力状态控制法指导该类多段索异形塔斜拉桥施工正装时，最终成桥状态是否会受影响。

(1) 临时外荷载

斜拉桥施工过程中，多道施工工序经常同步进行，作用于结构上的荷载除结构恒载外，由于施工作业需要，桥面上会出现许多临时荷载。为探究采用无应力状态法指导施工正装过程中临时外荷载的出现对成桥状态的影响，选取CJJ 11-2011《城市桥梁设计规范》规定的城—A级车辆荷载为临时外荷载，重轴布置于北岸跨跨中，在分阶段正装模型中，在S1终张拉阶段激活，并于S3终张拉时钝化。模型中临时外荷载施加见图7。

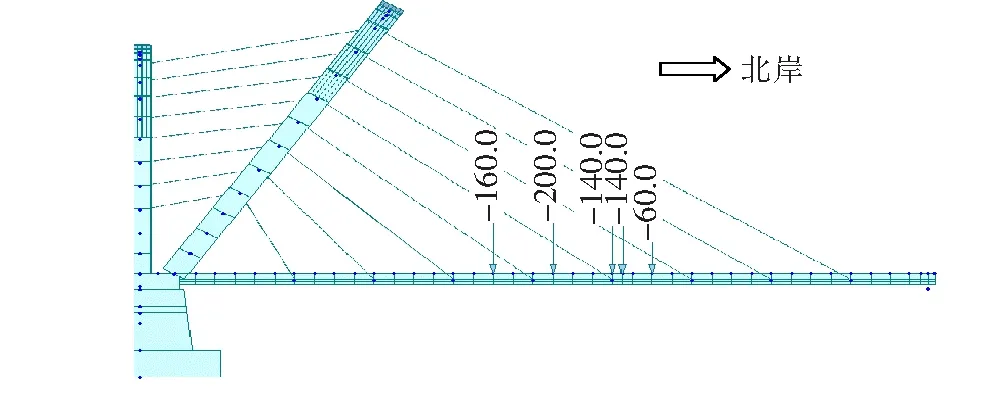
图7 临时外荷载施加示意图(单位：kN)

将原始分阶段正装模型成桥索力与临时外荷载影响下正装模型所得结果进行对比，如表7所示，虽部分量值有微小差异，但差值极小，两个模型所得结果可视为一致。

(2) 张拉顺序调整

为考虑斜拉索张拉顺序改变对最终成桥状态的影响，调整张拉顺序如下：塔间索初张拉顺序不变，初张拉完成桥塔脱离桥塔临时支架后，进行塔梁(斜拉)索由S1～S8的初张拉。主梁脱离主梁临时支架，二恒施工结束后，按照T1、S1、T2、S2、…、T8、S8的顺序依次进行塔间索、塔梁(斜拉)索的终张拉，成桥索力对比结果亦列于表7。结果表明：原始正装模型和施工顺序改变后的正装模型成桥索力一致。

5 结论

(1) 对于多段索异形塔斜拉桥的索力计算结果表明：多段索异形塔斜拉桥虽然各组斜拉索间存在复杂相互影响，各阶段斜拉索的张拉会引起其余斜拉索复杂的内力重分布，但斜拉索单元的无应力状态量只有在对应斜拉索张拉时才会发生变化。

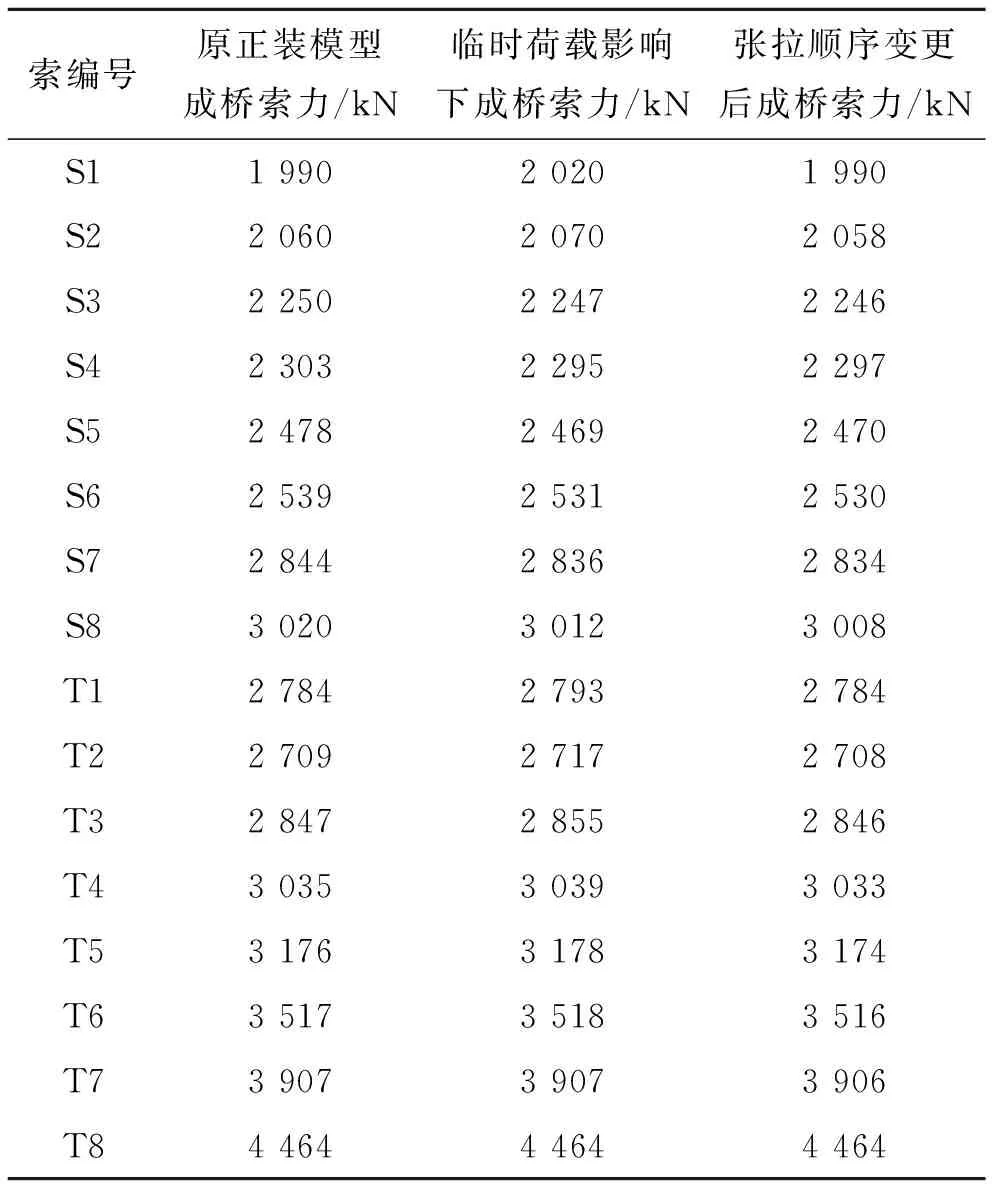
表7 成桥索力对比

(2) 所采用的增设部分中间施工控制状态能够有效简化该类桥型施工监控中的索力计算问题。只要确定合理成桥状态与中间施工控制状态的无应力状态量，将拉索的无应力索长于张拉时调整至相应施工阶段对应索单元的无应力长度，那么分阶段正装的成桥状态就能和一次落架模型的结果吻合。

(3) 所采用的结合无应力状态法进行多段索异形塔斜拉桥索力调整计算的方法能有效适应中间施工过程中发生的临时外荷载、张拉顺序变更等情况。依靠无应力索长值与索力间一一对应的关系，可在结构最终成桥状态与确定的合理成桥状态一致的前提下高效快速地得到各施工阶段拉索的张拉力，避免采用倒拆法、正装迭代法等“与建造过程相关”的中间施工状态计算方法所面临的繁琐试算、迭代过程，极大地提高了计算效率，推广了无应力状态法的应用范围。