基于CFD的巴歇尔槽进口连接段结构优化与水动力学特性分析
许虎,吴文勇,2*,王振华,乔长录,王秋良
(1.石河子大学水利建筑工程学院,新疆石河子832000;2.中国水利水电科学研究院,北京100048;3.深圳市水务规划设计院,广东深圳518000)
0 引言
【研究意义】水资源优化调配是农业节水灌溉的基础,做好灌区量水工作是保障灌区合理运营的关键。巴歇尔槽具有量测精度高、读数方便、不易淤积等优点,在我国灌区应用广泛[1]。水流由上游流经进口收缩段时,水位升高、流速增大形成临界流。此时上游水位与流量形成单一的函数关系,通过量测上游水位能够推求渠道流量变化[2]。
随着计算流体力学(CFD)的发展,数值模拟应用于水利工程设施的相关研究[3]。通过建立数值模型,能够将流体运动轨迹、流速、压强、温度等物理量清晰地呈现出来。相较于传统的模型试验,数值模拟具有适用性强、试验周期短、计算结果清晰等优点[4]。
【研究进展】近年来,国内外学者对各式量水装置进行模型试验与数值模拟分析,得出不同工况下槽内水流水力特性和试验结果。刘英等[5]、吉庆丰等[6]对不同体型圆柱形量水柱三维水流运动进行数值计算结果表明,水力参数的实测值与模拟值具有良好的一致性,在收缩比为0.63时,最大测流误差为4.95%,三维水流流态与试验结果一致。孙斌等[7]、宋金妍[8]、肖苡辀等[9]对不同收缩比的翼型量水槽进行流速场、水面线、水头损失、佛汝德数水力计算,认为收缩比为0.50~0.60 比较合理,并对机翼形量水槽翼面进行优化。张敏等[10]基于Flow-3D 软件对不同喉道长度的短喉道量水槽进行数值模拟选型,得出临界水深随喉道长度的增加而增加,短喉道量水槽较长喉道和无喉道量水槽水头损失小,且水流流态平稳,形式最优。侯莹等[11]、冉聃颉等[12]、景志芳等[13]对无喉道量水槽过渡段形式水力特性分析,建立流量公式,得出直线形过渡段形式测流精度高但水头损失大、圆形过渡段形式测流精度低但水头损失小,湍动能耗散主要在变比和底部区域,在测流范围内水头损失小于总水头损失的10%,试验值与模拟值相吻合。
数值模拟对量水堰的试验研究也同样适用,柳双环等[14]基于FLUENT 软件对U 形渠道三角形剖面堰数值模拟,得出不同底坡、渠道边坡、堰高下的水头损失,并对不同堰高拟合流量公式。叶青青[15]使用RNGk-ε湍流模型,VOF 方法对无喉堰在自由出流和淹没出流情况下拟合流量公式,通过数值模拟得出自由液面、流速、压力云图分布情况。【切入点】在实际工程建设中,巴歇尔槽与渠道上游连接段并没有明确的要求,目前常见的过渡段形式有圆弧段连接、斜面连接和无过渡连接。不同连接段形式对局部水头损失、水面线波动、测流精度有很大影响,在实际的输水过程中,连接段形式的选取决定了渠道输水效率高低与水资源配置决策。【拟解决的关键问题】本文采用数值模拟方法为巴歇尔槽连接段优化选型,为灌区巴歇尔槽的流道设计提供理论依据。
1 材料与方法
1.1 物理结构模型
采用标准设计尺寸(表1)和SolidWorks 建模软件建立喉道宽度为0.25m 巴歇尔槽三维物理模型。巴歇尔槽由上游收缩段、喉道段、下游扩散段组成,结构尺寸如图1、图2 所示。Z1 断面为巴歇尔槽俯视图(图1),巴歇尔槽上下游0.25m 处X1、X2 断面作为水力特性计算断面(图2)。置于宽度为1.10 m 的矩形渠道内,在上游收缩段和喉道段设置水位观测点,记录水位信息。

图1 巴歇尔槽俯视Fig.1 Parshall flume vertical view

图2 巴歇尔槽左视Fig.2 Parshall flume left view
上游收缩段与渠道采用4 种形式连接(图3),分别为方案1(内接圆弧过渡段)、方案2(外接圆弧过渡段)、方案3(直面过渡段)、方案4(无过渡段)。方案1、方案2 和方案3 进口连接段L1 长度为0.4m(3 种方案巴歇尔槽长度尺寸相同,故不在表1 中详细描述,统一由方案1 表示。),方案4 无连接段L1长度为0。

图3 巴歇尔槽上游连接段形式Fig.3 Parshall flumeupstream inlet connection section

表1 标准巴歇尔槽结构尺寸Fig.1 StandardParshall flumestructural dimensions
1.2 数学计算模型
明渠流动涉及气-液两相流动,VOF(流体体积)模型在处理多种互不交融的交界面时有很好的应用。在VOF 模型中,不同流体组分共用一套动量方程,对每一个网格流场计算时都记录下各组分所占有的体积率,跟踪自由流体表面[16]。在处理自由液面、分层流动、水坝决堤时有比较精确的效果。对于水气二相流场,假设水和空气具有相同的速度,在每个网格单元中,水和空气的体积分数之和为1,即:
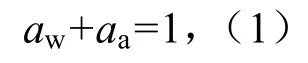
式中:aw、aa分别表示计算域中每一个控制单元内水和空气的体积分数(aw=1 时,表示控制体积内全部充满水;当aw=0 时,表示控制体积内全部充满空气)。
水气交界面使用连续性方程进行追踪,即:

式中:ui为速度分量;xi为坐标分量。
流体运动遵循三大守恒定律,即:质量守恒定律、能量守恒定律、动量守恒定律。明渠内水流为不可压缩流且黏性恒定,不涉及能量交换。对质量守恒定律和动量守恒定律的连续性方程和动量方程进行描述[17]。
连续性方程:

式中:ρ为密度;t为时间;u为速度矢量。
动量方程:
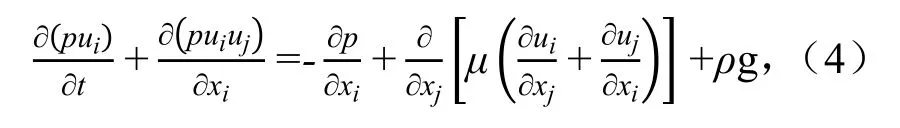
式中:ui、uj分别为x方向流速分量(i、j=1、2、3);p为静压力;t为时间;μ为黏滞系数;ρ为流体密度;g 为重力加速度。
明渠水流为充分发展的湍流,需要满足湍流输运方程。RNGk-ε湍流模型考虑了平均流动中的旋转流动,能够很好地处理明渠水流流线弯曲较大的情况。
湍动能k表示为:

耗散率ε表示为:
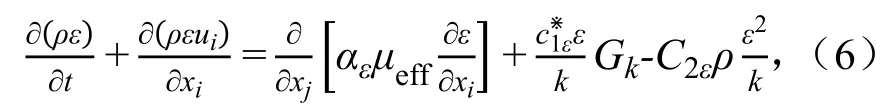
式中:k为湍动能(m2/s2);ε为湍动能耗散率kg/(m2·s2);μ为动力黏滞系数N/(s·m2);μeff为有效动力黏滞系数N/(s·m2),(μ与μt之和,其中αk=αs=1.39),Gk为平均流速梯度引起的湍动能k的产生项C2ε=1.68;i、j=1、2、3)。
1.3 网格划分与无关性分析
利用ANSYS18.0 软件进行网格划分,结构性网格具有网格节点分布规则、占用计算资源较小等优点,本次计算模型采用六面体结构网格划分。为了提高计算精度,更好地模拟近壁面水体流动特性,对壁面网格自下而上进行整体加密。为了确定网格单元个数及网格整体质量,将全局网格最大尺寸分别设定为0.05、0.04、0.03、0.02、0.01 划分网格。为了探究不同网格单元大小对于模拟结果的影响,对5 种尺寸的网格文件进行数值模拟计算。设置进口流量0.1m3/s,流速0.232m/s,渠道进口水深0.392m,求解方法与边界条件设置按照1.4 部分内容。分析计算结果:当网格最大单元尺寸小于0.03 以后,上游水深不再随着网格加密发生变化(表2)。因此选用最大网格尺寸大小为0.03 对模型网格划分(图4),网格整体质量在0.7 以上。4 种方案下网格单元个数分别为303452、303918、303726、301794。

表2 网格无关性分析Fig.2 Analysis of meshing independence
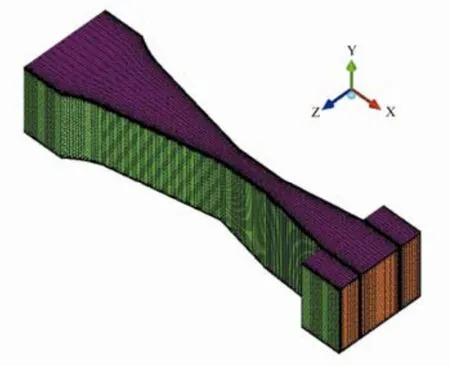
图4 六面体网格划分Fig.4 Hexahedral meshing
1.4 数值求解方法与边界条件
1.4.1 求解方法
数值模型基于三维稳态压力法求解器,VOF 方法,对Y 方向设置重力-9.81m/s2。基本控制方程为N-S 方程,采用RNGk-ε湍流模型计算。采用一阶迎风格式离散,PISO 算法进行流场计算,对全局区域进行初始化,设置残差收敛值为0.0001,迭代步数为1000 步。
1.4.2 边界条件
在自由出流情况下分别设置来流流量:0.01、0.05、0.10、0.15、0.20m3/s。渠道进口分别设置气液两相,空气相采用压强入口,默认为标准大气压强、水流相采用速度入口,分别设置进口流速和水力直径、出口设置为自由出流、壁面设置为标准无滑移壁面。
2 结果与分析
2.1 模型合理性验证
为了验证数值模型和边界条件能够满足实际工况,对方案1 模型进行数值模拟并与文献试验结果进行对比分析(文献试验模型为喉道宽度为0.25m 的标准巴歇尔槽,与方案1 模型结构尺寸一致),比较二者误差[18]。上、下游水深与流量通过对计算结果进行数据处理得到。如表3 所示,数值模拟结果与模型试验结果最大误差小于5.22%,表明此次模型选取较合理,能够满足数值模拟计算。

表3 数值模拟结果与试验结果误差分析Fig.3 Error analysis of simulation results and test results
2.2 水力特性分析
2.2.1 水面线与流线
运用Tecplot 软件对模拟结果进行后处理分析,取Z1 断面作为研究断面,图5 为过流流量为0.1m3/s时,4 种方案的巴歇尔槽水面线模拟情况。水流由渠道进口流经至上游收缩段,由于流道束窄形成雍水水位升高,此时水流流速增大形成临界流。水流由喉道段流经至下游扩散段,流道扩宽形成跌水水位降低,此时水流流速减小流向下游。4 种方案整体而言,喉道段前后水位落差较大,流线曲率变化在此处达到极值。水流方向发生较大的改变,分子间相互作用加剧,动能转化为内能,水头损失较大。方案1、方案2、方案3 由于过渡段的存在水流流线较为平缓;方案4由于没有过渡段连接,水流流线在渠道与巴歇尔槽交界处有较大的起伏。
2.2.2 局部水头损失
依据不可压缩流体恒定总流的能量方程,对巴歇尔槽上下游水头损失计算。由于沿程渠道较短,沿程水头损失相对于整体水头损失比值过小,不予考虑。取上下游断面X1、X2 断面作为计算断面,其能量守恒方程为[19]:

式中:z1、z2分别为上下游液位高度(m);p1、p2分别为上下游静水压强(kN/m2);γ为流体重度(N/m3);α1、α2分别为动能修正系数,取值为1,v1、v2分别为断面平均流速(m/s);g 为重力加速度,取值为9.8 m2/s,hw1-2为上下游水头损失(m)。

图5 4 种方案水面线Fig.5 Four schemes for surface lines
由表4 所示,4 种方案下的巴歇尔槽局部水头损失与流量之间关系,局部水头损失随着来流流量的增大而增加。4 种方案平均水头损失:方案4>方案2>方案3>方案1。方案1、方案2 采用弧面过渡,水流流经圆弧壁面形成2 个分力。一部分分力垂直于壁面,产生损耗;另一部分分力平行于壁面,汇入主流。方案4 无过渡段直接采用边墙连接,水流流动方向垂直于边墙发生撞击,动能转化为内能,水力损失最大。

表4 不同流量下4 种方案水头损失Fig.4 Head loss of four schemes under different flow rates
2.2.3 测流精度分析
依据《JJG(水利)004—2015 明渠堰槽流量计计量检定规程》流量计算公式,对4 种方案巴歇尔槽水流流量进行计算。自由出流情况下,流量与上游水头呈现单一的因变关系,流量计算式为:

式中:Q为流量(m3/s);C为流量系数;h为上游实测水头;n为指数。
由表5 所示,4 种方案巴歇尔槽测流精度相对误差分析,测流精度相对误差随来流流量的增大而减小。
当来流流量较小时,上游液位较低,液位高度读数误差相较于液位高度占比较大,因而产生较大的流量计算误差;当来流流量增大时,上游液位较高,液位高度读数误差相较于液位高度占比较小,流量计算误差变小。方案1、方案2、方案3 由于过渡段的存在,能够发挥引导来流水流的功能,使上游液位波动范围较小,读数精度较方案4 更加准确。通过对4 种方案巴歇尔槽测流精度平均误差计算得出结论:方案4>方案2>方案1>方案3,方案3 连接形式的巴歇尔槽有较高的测流精度。

表5 不同流量下4 种方案测流精度相对误差Fig.5 The relative errors of measuring accuracy of four schems under different flow raters
2.3 流场分析
2.3.1 速度
取Z1 断面作为研究断面,图6 为过流流量为0.1m3/s 时,4 种方案巴歇尔槽纵剖面速度云图。水流流速沿渠道进口至渠道出口方向依次增大,流速梯度变化明显。水流流速大小与流道宽度成反比,流速变化引起水流流态由缓流向急流过渡,在喉道附近形成临界流,达到测流目的[20]。在水流与空气交界处,水面波动引起空气局部范围内的扰动,产生较小的流速变化。

图6 4 种方案速度Fig.6 Four schemes forvelocity
2.3.2 压强
取Z1 断面作为研究断面,图7 为过流流量0.1m3/s 时,4 种方案巴歇尔槽纵剖面压强云图。静水压强随着水深的增加而增大,压强梯度变化明显。渠道上游雍水,上游连接段处静水压强最大。在巴歇尔槽的安装施工过程中,应当在上游连接段处衬砌加固,防止因静水压强过大导致巴歇尔槽物理结构变形而产生测流误差。
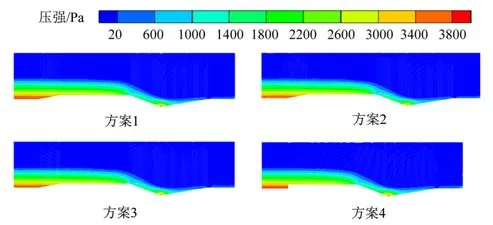
图7 4 种方案压强Fig.7 Four schemes forpressure
2.3.3 湍动能
取Z1 断面作为研究断面,图8 为过流流量0.1m3/s 时,4 种方案巴歇尔槽纵剖面湍动能云图。湍动能数值较大处皆位于气相所分布的区域,因为气体相较于液相有更大的流动性与扩散性,分子间的能量交换与传递更强烈。湍动能数值最大处位于水流与空气交界处,由于水体运动带动水气交界处空气做相对运动,气体分子间做剪切运动产生摩擦力,消耗内能。水相区域的湍动能分布沿着水流方向有增大的趋势,流道的突扩和突缩改变水流的流动方向使水体内产生旋涡,液体分子之间发生大量无规律的碰撞与摩擦,消耗水流能量。湍动能数值较大处一般位于分子运动活跃的区域。

图8 4 种方案湍动能Fig.8 Four schemes for turbulent kinetic energy
3 讨论
巴歇尔槽普遍应用于我国大中型灌区,上游连接段作为流道的一部分,在施工过程中考虑其最优形式尤为重要。巴歇尔槽进口连接段形式一方面要考虑测流精度、水头损失的因素,另一方面也要根据渠道断面形状、施工条件来决定。内接圆弧过渡段形式水头损失小,直面过渡段形式测流精度高[11],无过渡段形式水头损失较大、测流精度低。
本文研究发现巴歇尔槽在来流流量小的情况下,测流精度较低,为了保证较高的测流精度应在来流流量较大的情况下进行流量量测工作。局部水头损失随着来流流量的增加而变大,流速云图与压强云图分布符合水力学定律,水流在喉道段由于流道缩窄形成临界流此时流速最大,静水压强与淹没水深呈线性关系,随着水深的增加而变大。湍动能大小衡量分子间能量、动量的传递关系,气体相较于液体有更强的流动性与扩散性。气体分子的活跃度与无规律运动更加强烈,因此耗散性更强。
从工程建设方面考虑:由于流道上游雍水的缘故,上游连接段处静水压强最大,在安装过程中对此处进行加固,防止流道变形沉降。数值模拟具有成本低、计算结果准确、后处理可视化等优点,能够应用于水利工程的建设。文中仅对自由出流情况下的巴歇尔槽进行水力特性数值模拟分析,后期将对淹没出流情况下的巴歇尔槽进行水力特性数值计算,并比较二者之间的差异。
4 结论
1)采用进口连接段过渡的巴歇尔槽相比无连接段过渡的巴歇尔槽水流流线更加平缓、起伏较小。
2)内接圆弧过渡段形式巴歇尔槽局部水头损失最小、无连接段过渡的巴歇尔槽局部水头损失最大。
3)为提高测流精度,巴歇尔槽上游连接段宜采用直面过渡形式。
4)巴歇尔槽纵剖面速度云图与压强云图变化梯度明显,流速最大处位于喉道段、静水压强最大处位于上游雍水段,湍动能数值较大处位于流体运动活跃的区域。

