国际产业转移对各国碳排放的影响研究——基于多区域投入产出模型

董 聪 王 晨 董秀成

（1.对外经济贸易大学国际经济贸易学院，北京 100029；2.博科尼大学经济系，米兰 I-20136）

一、引言

20世纪80年代以来，经济发展的迅猛态势和贸易全球化的兴盛深刻地改变了世界经济面貌，贸易分工和跨国生产已经成为世界经济发展的主要推动力（Hummels等，2001）。[1]许多国家积极参与世界分工，借由经济全球化的浪潮迎来了本国发展的良好机遇。然而日益凸显的一系列环境问题也伴随经济发展而来，气候变化问题甚至威胁到了人类的生存和发展。二氧化碳的控制减排已不再是简单的科学议题，而是成为了各国发展所要角力的重要环节。当发展中国家参与全球分工，成为国际产业转移的目的地时，部分学者针对这一现象提出污染避难所假说（Walter，1979），[2]即认为污染密集型产业会从环境规制水平高、排污成本高的发达国家流向规制水平低、排污成本低的发展中国家，从而使发展中国家成为转移污染的避难所。加之国际环境有关提议的主要目标基本都是以生产过程的排放为核算对象，从而使得产品进口国满足自身消费需求的同时，又避免了二氧化碳等温室气体的减排责任，因此国际间产业转移无疑会加剧东道国的碳排放总量。另一部分学者却持不同意见，他们认为由于伴随着产业转移存在技术“外溢效应”，产业转移不一定会引起碳排放的增加。如Antweiler等（2001）从一般均衡视角研究贸易对污染排放的影响，认为技术水平的提升会抑制贸易产生的污染，得出进行国际贸易对环境有利的结论。[3]

以我国为例，改革开放以来，尤其是加入WTO之后，中国迅速融入世界经济体系，参与国际分工，在一段时间内一直被冠以“世界工厂”的称号，在世界经济中扮演者越来越重要的角色。与此同时，中国的二氧化碳排放量在2008年正式超过美国，跃居世界第一位。在碳达峰和碳中和目标下，中国面临的减排压力也与日俱增。由于接纳了国际间能耗较高、污染较重的产业，高污染、高能耗产品占据了相当部分的出口贸易份额，中国赢得贸易顺差的同时，也排放了大量污染物，为其他国家背负了碳排放压力。

避免国界或者关境对减排政策的割裂，对全球每个国家、每个部门的碳排放进行深入研究，以全面了解碳排放的增长和影响因素尤为必要（赵忠秀等，2018）。[4]本文借鉴了隐含碳研究中的多区域投入产出模型，核算各国与部门碳排放，而后对碳排放进行结构分解，将由国外因素（包括国外需求因素和国外技术因素）所拉动的碳排放增加值剥离出来，探究其与各个国家在世界范围内产业转移的关系和影响，希望将国际产业转移的影响通过本国碳排放体现出来，以期为政府相关部门在环境治理、节能减排及产业转移和承接方面提供政策参考。

本文的创新之处在于：首先，部分已有文献在研究碳排放与贸易、产业间的关系时，以一国碳排放总量来进行探究，将本国需求、技术原因所拉动的碳排放增量与国外原因所带动的碳排放增量分离开来，更精确地对外部原因进行定位。其次，由于技术溢出效应带来的产业减排，许多产业转移与环境污染领域的研究受到不同程度的干扰，随着产业转移而来的节能减排技术能否对本国碳排放产生影响，如果产生影响，效应又如何衡量，本文采用SDA分解法将国外因素中的技术影响剥离开来，使其后的实证数据更加可靠，并由此对技术转移的影响进行量化探究。此外，为进一步验证回归结果的可靠性，本文从三个角度设置不同的假设，通过稳健性检验，模型结论的有效性得到证实。最后，将不同年份的投入产出表进行比较分析，以动态视角反映社会生产中需求、技术的变化过程，模型所采用数据均为基期与报告期的变化值，因此在数据的规范性和稳定性上具有一定的优势。

二、文献综述

在近年来关于碳排放的研究中，隐含碳排放已成为研究热点（张中华等，2019），[5]本文对隐含碳排放模型多有借鉴。当前针对隐含碳的核算方法主要有三种：直接排放核算法、基于完全需求系数测算法以及基于完全消耗系数测算法（王媛等，2012）。[6]除第一种外，其余两种都属于投入产出分析法，这一分析方法由里昂惕夫在20世纪三十年代提出，通过投入产出表的编制及相应模型的建立，投入产出法可以用来反映经济体中多个部门的产业间相互关系。在能源、环境的相关研究中，它常被用来追踪产品的全部能源消耗及二氧化碳排放量，是宏观视角下研究经济体碳排放的主流方法。

在针对某一个国家的研究中，单区域投入产出模型（Single Regional Input-Output Model）常被用来对该国碳排放情况进行测算。朱启荣（2010）藉由中国2002年和2007年投入产出表对出口贸易活动产生的二氧化碳排放量进行了测算，同时对我国出口贸易结构所存在的问题进行了分析。[7]邓荣荣（2014）基于非竞争性可比价投入产出表，对我国1997-2011年碳排放情况进行了测算，结果显示出口含碳量的增长速度高于进口含碳量。[8]除了单区域投入产出模型，也有学者运用双边投入产出模型（Biregional Input-Output Model）来对两个国家或区域的贸易情况进行研究，以探寻环境或二氧化碳排放问题。Bin和Robert（2006）定量测算了1997-2003年美国出口到中国商品中的隐含碳排放量。[9]王菲等（2012）通过双边投入产出模型分析了中日间贸易的碳排放情况，结果显示中国为日本承担了巨大的消费型隐含碳排放。[10]然而，在世界多个国家深度参与贸易全球化的背景下，双边投入产出模型自身容易存在不可避免的误差，因此多区域投入产出模型（MRIO）在多个国家或地区贸易隐含碳排放的研究中备受学者欢迎。庞军（2014）基于GTAP数据库建立MRIO模型，对中欧二氧化碳排放量以及行业排放分布进行量化，发现中国是典型的隐含碳排放净出口国，欧盟则相反。[11]为了利用世界范围内的样本来探讨碳排放随产业的转移，本文采取基于完全消耗系数测算法的多区域投入产出模型。

近年来经济生产中二氧化碳的排放问题日益受到各国政府重视，国内外学者对碳排放影响因素的研究逐渐增多。其中，因素分解法在世界多个国家和地区的碳排放领域得到广泛应用，是一种以比较静态分析为理论背景的方法。其基本思想就是将目标变量在基期到报告期的变化量分解成为数个影响因素的变动组合，以此剥离出各个影响因素对于目标变量的作用方向和影响大小，进而比较得出推动或阻碍目标变量变化的驱动或抑制因素。常见的因素分解法有指数分解法（IDA）和结构分解法（SDA）。SDA的劣势在于其对于数据的更高要求，但优势在于基于投入产出表它可以全面分析各类直接或者间接影响因素，尤其是能够将一个部门需求变动所带来的间接影响反映到其他各个部门中。本文采用SDA分解法作为碳排放变动的主要分解方法。

最早将投入产出结构分解法引入能源、环境研究领域的是里昂惕夫（1970），[12]随后许多学者纷纷效仿。结构分解模型通常有4种形式：保留交叉项；不保留交叉项，将其以不同方式分配给自变量；加权平均法以及两级分解法。“由于不同的分解形式产生的结果存在差异，并且理论上没有理由认为某种分解形式优于其他，可通过不同分解形式求出每个因素影响效应，然后求出其平均值，以此解释目标变动”（Dietzenbacher和Los，1998）。[13]将投入产出模型与结构分解技术相结合的投入产出的结构分解模型（IO-SDA），因其能对经济系统中的总量变动、结构变动等问题进行分析，所以被广泛应用于国际贸易、经济增长、环境保护和能源应用等领域。为了尽可能降低分解结果的误差，本文在SDA分解法方面有所借鉴，选择采用两级平均分解法来对各个因素的影响效应进行定量研究。

正如引言所说，关于国际产业转移对碳排放的影响，目前的观点分为对立的两类。Walter等（1979）提出“污染避难所”的假说，[2]后经过Baumol和Oates（1988）进行了完善。[14]然而Smarzynska和Wei（2001）的研究却没有找到可靠证据来证实污染避难所假说。[15]另一类观点以产业转移中存在技术“外溢效应”为由，认为产业转移会减缓碳排放。陈楠、刘学敏、长谷部勇一（2016）对中国和日本的产业转移中的碳排放问题进行研究，发现由于能源使用效率的提升和生产技术的改良，中国在承接了日本高碳排放水平的产业后，并没有成为污染者天堂。[16]国内学者对区域产业转移对碳排放影响的研究较晚一些。肖雁飞等（2014）对我国2002-2007年间区域产业转移的碳排放转移进行分析，发现产业转移对碳排放的影响和地区差异性有关，在于承接地的产业选择和产业结构在转移中的优化水平。[17]成艾华（2013）分析了我国28个省市的碳排放强度变化随区域产业转移的情况，结果显示净转入地区的排放强度不断增加而碳排放净转出地区的强度不断降低。[18]

在上述关于产业转移和碳排放变化的研究中，不难发现，利用一国的单区域投入产出模型，或者双边投入产出模型来进行的研究，不能对产业转移与碳排放的关系做出一般性规律的总结，来反映我国在全球视角中的产业发展和节能减排关系。本文借鉴隐含碳研究中的多区域投入产出模型，结合SDA分解法，从更广阔的视野对国际间产业转移所造成的国家碳排放影响进行分析。另外，本文并不聚焦隐含碳转移及核算这一主题，而意在通过分解法测算国外拉动效应来解释国际间经济发展对各国碳排放的影响。

三、模型设定与数据来源

(一)模型设定

1.全球碳排放的投入产出模型

对于全球投入产出模型：首先，横向关系上，某一国家的某一部门分别为各个国家的不同部门用于生产的中间产品和最终需求产品；纵向关系上，来自各个国家各个部门的产出投入到某一国家某一部门的总产出中。

假定全球共有I个国家，每个国家有S个部门，第i个国家第s个部门的产出是yi（s），第i个国家第s'个部门对第j个国家最终需求的贡献为fij（s），第i个国家第s个部门对第j个国家第s’个部门的投入为zij（s，s’）。

进一步地，Zij为第i个国家向第j个国家各个部门中间投入矩阵，Fij为第i个国家向第j个国家最终需求的输出矩阵，Yi和Vi分别为第i个国家的总产出矩阵和增加值矩阵，如下式所示：

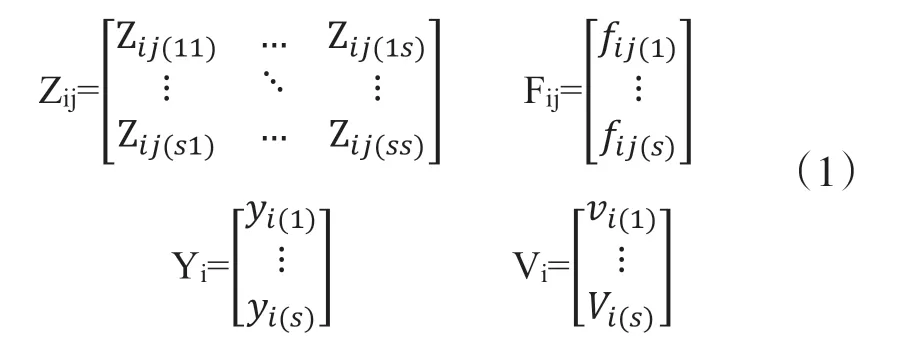
得到相应的投入产出表结构如表1所示：

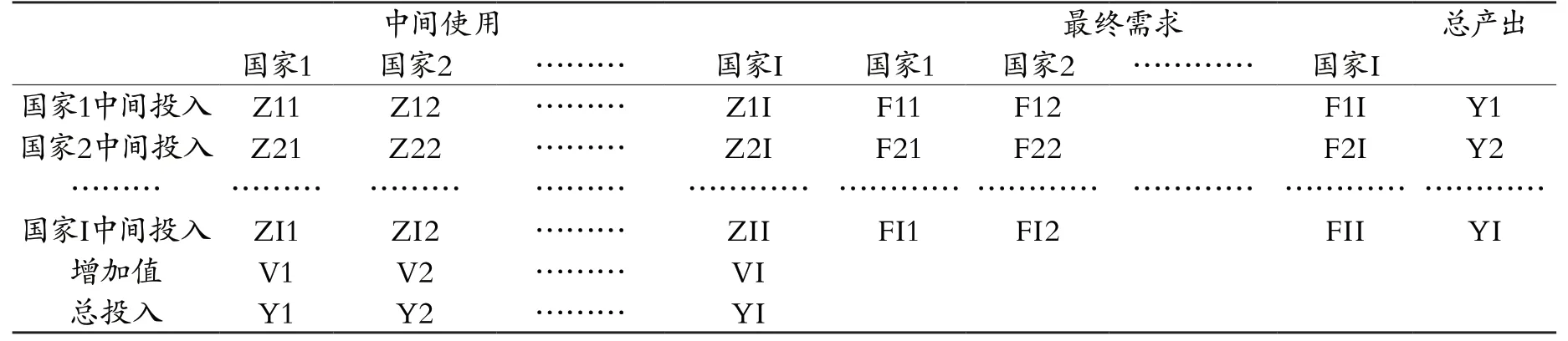
表1 世界投入产出表结构

根据表1得出，第j个国家第s’个部门产出对 第i个国家第s部门投入的直接消耗系数：

设Aij表示第j个国家的产出中，来自第i个国家的投入的直接消耗系数矩阵：

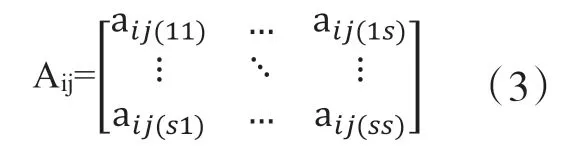
则世界投入产出模型的直接消耗系数矩阵A为

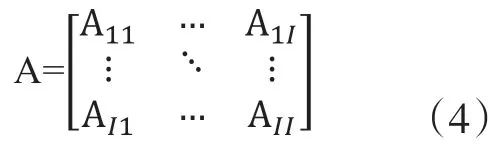
根据投入产出模型可知：

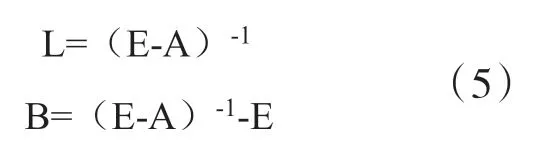
其中，L为里昂惕夫逆矩阵，B为完全消耗系数矩阵，E为SI*SI的单位矩 阵。

完全消耗系数可以在描述i部门对j部门直接投入的同时，进一步说明第i部门通过对其他部门投入而对第j部门的间接投入，这在分析各产业转移以及伴随其移动的碳排放时很关键。

由于世界各国分行业能源消耗的数据可得性问题，加之本文研究重点在于碳排放的影响因素而非核算标准，因此这里直接以各国分年份碳排放量除以当年总产值，即单位GDP碳排放强度（Carbon Intensity）来计算各国各产业的排放值。具体表示为：

其中CIi表示i国的碳排放强度，Ci表示i国该年份的碳排放总量，Yi表示i国总产出，则

其中ci（s）为i国s产业的碳排放量，yi（s）即上文所提到的第i个国家第s个部门的产出。

将研究期间每年的投入产出表都依次处理，得到每年的碳排放投入产出表。

2.投入产出表的结构分解

结构分解法发展比较成熟，本文主要根据Miller和Blair（2009）的经典论述和框架，[19]同时参照袁志刚和饶璨2014将影响因素再按照国内外进行区分。[20]本文结构分解模型先将投入产出表中各国各行业总产出变化分解为来自最终需求影响和来自技术变化影响，其次将最终需求影响划分为水平效应（最终需求变动影响）、混合效应（同一国家的最终需求在不同产出之间的分布变化）以及分布效应（不同国家最终需求之间的分布变化），最后再将三种不同的终需变动和技术变动都按照国内国外进行分解，最终得到国内外技术变动和终需变动对产出变化的影响。

设世界投入产出模型最终需求矩阵F和总产出矩阵Y为：

根据SDA分解模型的两级分解办法，将第一期的向量上标设为0，第二期的向量上标设为1，得到方程式如下：

其中，△L代表技术水平变动，△F代表最终需求变动，即这两项分别代表技术变动、总需求变化对某一行业产出变化的影响。

首先探讨总需求变化对某一行业产出的影响。假设 f 为所有国家消费之和：

因此，每一个国家最终需求占最终需求的比重矩阵D（44*1阶矩阵）为：

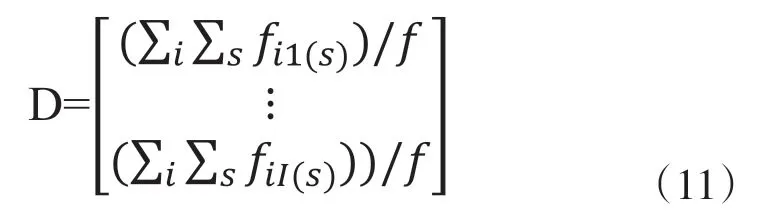
所有国家各个部门产出用于每一个国家最终需求的比重矩阵B（2464*44阶矩阵）为：

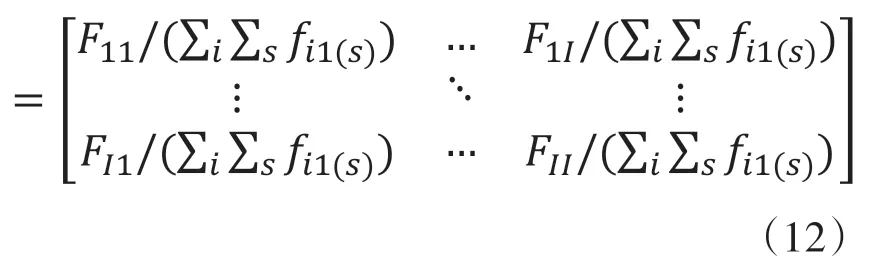
在此基础上，针对国内、国外的总需求变化对最终产出的影响对模型进行再分解。以中国为例，则中国与其余国家（外国）总最终需求变化量为：

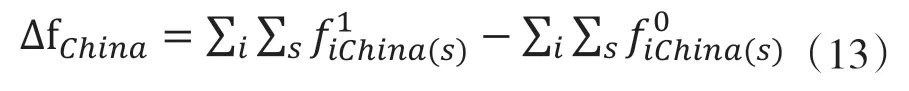
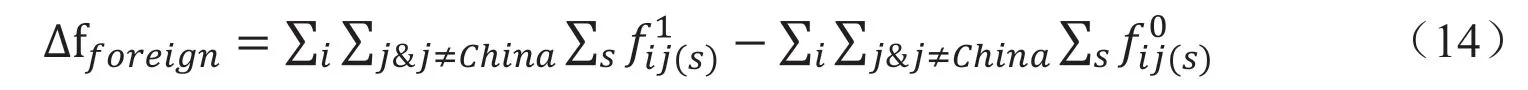
中国与其他国家最终需求占总最终需求的比重矩阵为：

所有国家各个部门产出用于中国最终与其他国家最终需求的比重矩阵为：

由以上各式可确定△F的计算方程，即国内外最终需求变化对总产出的影响:

接下来探讨技术变化对行业总产出变化的影响。同样考虑国内与国外两方面的技术变动影响，可得：

其中△AChina、△Aforeign分别代表国内（外）技术变动的完全消耗矩阵。

对上述方程式进行整合，最终可得到制造业的结构分解式为：

即最后所有国家各行业的变动由此分解为中国技术水平的变动、国外技术水平的变动、中国最终需求变动的水平效应、国外最终需求变动的水平效应、中国最终需求变动的混合效应、国外最终需求变动的混合效应、中国最终需求变动的分布效应与国外最终需求变动的分布效应。因本文仅需要考虑国外最终需求因素，故将三种最终需求变动效应加总来进行分析。

本文选取2000—2009年这十年的投入产出表，将单位产出碳排放强度带入该模型，除去数据不可得的台湾地区，得到42个国家和地区各自的56个部门在九个时间段内各因素对碳排放变化量的影响。最后将计算得出的各个产业因各因素而变化的碳排放量按照国家进行加和：

其中，△DfCi表示i国家因国外需求因素而产生的碳排放增量，△DfCi(s)表示i国家s部门因国外需求因素产生的碳排放增量；同理，△TfCi表示i国因国外技术因素而产生的碳排放增量，△TfCi(s)表示i国s部门因国外技术因素而产生的碳排放增量。

3.产业转移的核算方法

在产业转移方面，本文主要借鉴孙晓华（2018）所描述的产业转移衡量方法，[21]同时参考孙植华（2018）的产业动态集聚指数。[22]为了使其适应本文模型，此处将模型略做改动，设产业转移指数反映某一产业在一定的时间段内向某一个地区集聚的速度，能够将产业的区域转移方向和能力体现出来，同时能够与之前的动态碳排放变化模型相匹配。具体公式为：

如上所示，0、t 表示时间周期，sist表示i地区中s产业的平均增速，sit表示世界范围内j产业的平均增速，eist和eiso分别表示报告期和基期s产业在i地区的总产值，n表示世界上共有n个国家和地区。ITIist表示产业转移系数，若数值为正，则i 地区s 产业在世界平均水平下是发展的；反之若为负，说明该产业在i 国萎缩。

最后将各个国家的部门按照该部门占国家总产出占比加权，核算出各国的产业转移系数：

其中ITIi是i国在基期和报告期之间的产业转移指数，ITIis表示i国s部门在基期和报告期之间的产业转移系数。其中t 为基期到报告期经过的周期。

4.计量模型

由于本文的因变量与核心解释变量均为基期和报告期的变化量，因此控制变量也都处理为期间内的变化值，以使模型更加合理。具体的回归模型如公式（30）所示：

其中，△DfC是某国因国外需求因素而在核算期间内增加的碳排放量，ITI为该国这一期间内产业转移指数。由于前者数据规模较大，进行取对数处理。而后者计算所得指数较小，采取扩大一万倍之后取对数的模式。△GDPpc表示人均GDP变化量，△U表示城市化变化量，△RE表示可再生能源与核能变化量，△Epc表示人均耗电变化量，△ECpGDP表示单位GDP能耗变化量。

被解释变量是国外因素所导致的本国碳排放增长。考虑到国外因素影响传递到国内时会随着各国国情的不同而有所差异，因此参考已有文献，选择上述控制变量。

（二）数据来源

利用计量模型来研究世界各国因国外因素而增加的碳排放量与国际产业转移之间的关系。首先选用来自WIOD数据库的2000年—2010年①2000-2001年为时间段1，以此类推。世界投入产出表作为模型基础②世界投入产出数据库：http://www.wiod.org/home，加之Word Bank数据库获得的世界各国碳排放总量③世界银行数据库：https://data.worldbank.org.cn/，以计算因变量，即各国因国外因素而增加的本国碳排放量。另一方面，基于投入产出表计算得到各国产业转移指数。首先，人均GDP可以较为客观的反映一个国家人民的生活和消费水平，数据来源自IMF④国际货币基金组织数据库：https://www.imf.org/en/Data。其次，作为一个国家，城市化程度也很大程度上影响了碳排放量。类似的，城市化水平也与碳排放有所关联，高城市化水平可能会使得社会耗能增加，但也可能会推出一系列城市治理政策以减免碳排放。人口密度与城市化数据来源于世界银行数据库。除此之外，可替代能源和核能、人均耗电量以及单位GDP的能源消费也同时被考虑在内。可替代能源和核能的使用或许能对国家碳排放起到减缓作用，而电力的煤炭消费量占煤炭总消费量的比重一直很大，且在不断上升。考虑到人均耗电量中包含许多风能等可再生能源，本文加入单位GDP能源消费的控制变量，数据来自世界银行数据库。⑤本文所有数据均为部门级数据，因“产业转移”名词所限，本文的产业皆指部门。

四、实证结果

（一）描述性统计

图1 部分国家二氧化碳排放变化量（千吨）

如图1所示为部分国家碳排放变化量随时间的变化情况。限于篇幅，这里仅从发达国家与发展中国家列表中各选取几例作为代表。发达国家二氧化碳排放量普遍呈现出下降趋势；而发展中国家，如中国、巴西、印度、印尼等，其二氧化碳排放量却呈现出波动态势，增减不一。

由第二部分描述的模型可得九个区段内42国家56 个部门的国外需求拉动碳排放量与部门产业转移指数的关系，如图2所示：

表2表示变量的描述性统计。

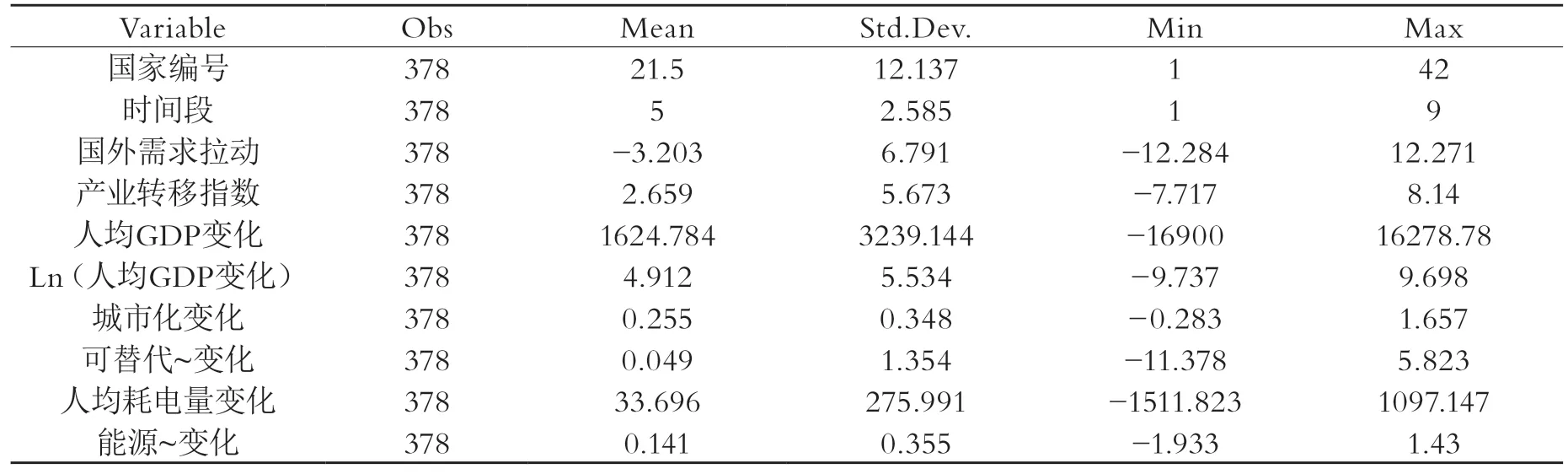
表2 描述性统计

（二）回归结果

通过Hausman检验和LM检验，结果显示混合效应优于随机效应和固定效应。借助Stata软件得到回归结果如表3所示。

表3 混合效应回归模型结果

回归结果通过了VIF共线性检验，计量回归模型有效。根据表3的实证结果，除去最后一列回归，主要研究变量基本是显著的。

在第一列回归结果中，主要研究变量l n（ITI）在1%的水平上显著为负，然而系数的符号和本文预期情况相反。即随着产业的迁入，国外需求对本国的碳排放量有抑制作用。在第二列回归结果中，新加入的城市化变化率在10%的水平上显著为正。逐次加入其他变量，通过第三、四列回归结果发现，单位GDP能耗并不显著，因此剔除。第三列是结果比较理想的回归结果。结果显示，城市化和人均耗电量的变化与外需拉动的碳排放变化呈正相关关系。或许是因为城市化和人均耗电量从一定程度上反映了一个国家能源使用的水平和效率，因此当国外需求增加时，一个国家的能源使用和污染情况通过国内产出增加而体现出来。另一方面，可再生能源与核能在10%的水平上显著为负，即这一指标和产业迁移指数对碳排放都有抑制作用。显然，可再生能源和核能的使用对于环境污染有着很好的抑制作用。然而，主要研究变量的系数为负，这与本文的预期结果并不相符。

针对这一问题，本文有如下猜测：①由于样本中，发达国家和发展中国家并未区分，而发达国家可能会有选择的迁入具有发展前景的低污染产业，因此对回归造成了影响。②相对于用SDA分解法将国内因素剔除的因变量，产业转移指数却并未将国内因素排除在外。国内本身的产业转移和壮大将会一定程度上影响回归结果。本文会在接下来的稳健性检验中进一步探讨这一问题。

五、稳健性检验

（一）将国外技术变化纳入模型

在第二节提到的结构分解模型中，将引起本国碳排放增加的国外因素分成了技术和需求两个部分。在前一节的计量模型中，将技术因素剥离了出去，得到了“产业迁移对国内碳排放有抑制效果”这一结论。为了测试其稳健性，进一步探索国外因素的影响，这里对技术因素和国外所有因素，即需求和技术的加总，分别进行计量回归。

首先将因变量设置为国外技术需求引起的碳排放增加（lnΔT_fC），将控制变量依次加入模型，其回归结果如下：

表4 第一次稳健性检验（1）

回归结果表明：在第二列中，城市化变化量这一控制变量并不显著，因而在后面的回归中剔除。主要研究变量即ln（ITI）在所有回归中都十分显著，且系数均为负。因而可以确定，国外技术的转入确实会对本国碳排放产生显著的抑制效果。技术溢出效应在这一模型下是成立的。控制变量中，人均GDP变化量，可再生能源变化量以及单位GDP能源强度的系数都为负。人均GDP的增长代表着国民生活水平以及国内能源使用率的提升，同时更好的生活有利于培养国民的低碳意识，因而其增长对碳排放有抑制作用。另一方面，人均耗电量的提升确实促进了本国碳排放量的增长。

将因变量替换为所有国外因素导致的碳排放变化量：

表5 第一次稳健性检验（2）

可以看到各变量回归结果依旧显著。相比较表一中的基本回归结果，产业转移对碳排放的影响程度有所降低；R square有所提高，说明加入技术水平的模型对现实的拟合程度更高。经过上述检验，“产业迁移对国内碳排放有抑制效果”这一结论更加稳健，说明两者之间确实存在紧密联系。然而其影响方向与预计情况相反的问题依旧没有得到解释。

（二）区分各国的发展程度

由于样本中的各个国家和地区发展水平有极大差异，接下来按照国际标准将发达国家区分开来，分别进行回归。该区分标准综合了HDI VH联合国开发计划署人类发展指数极高的国家；WB HIE世界银行高收入经济体；IMF AE国际货币基金组织发达经济体；CIA AE中央情报局《世界概况》发达经济体等。

发达国家和发展中国家回归结果分别如表6、7所示。首先，将上述两表与原回归结果相比较，不论是发达国家还是发展中国家，回归结果中各个系数的符号都没有改变。对于发达国家而言，产业转移和可再生能源使用这两个变量对碳排放的影响更大一些，而城市化对碳排放的影响不再显著。较之发达国家，发展中国家国外因素对本国碳排放增量的影响幅度在本文的模型量纲下多出了30%左右。对于发展中国家而言，产业迁移对碳排放的影响也有一定增加，同时城市化和人均耗电量这两个因素的系数显著增加。显然，对于发展中国家而言，城市化和耗电量的发展会更多的影响到碳排放。另外，可再生能源的使用这一因素不再显著，很可能是这类能源在发展中国家的使用非常有限而导致的。

表6 第二次稳健性检验（发达国家）

表7 第二次稳健性检验（发展中国家）

（三）对产业转移指数的进一步细化

在原模型中，产业转移指数的计算借鉴了孙晓华（2018）中的研究方法。然而相对于用SDA分解法将国内因素剔除的因变量，产业转移指数却并未将国内因素排除在外。在一个特定国家，尤其是发展中国家，国内某一产业若能发展壮大并融入世界经济体系，则其自身比较优势以及资金、政策的倾斜等都会提供非常可观的贡献。而随着该国技术水平的发展，在发展产业的同时逐渐控制该产业的污染情况也就变得顺理成章。为了排除这一干扰，下面对该变量的模型进行调整。

考虑到投入产出表中各个国家之间的紧密联系，这里采用完全消耗系数矩阵来进行处理。将完全消耗系数矩阵按照各产业产值加权，而后将对角线上本国的中间品投入矩阵替换为0矩阵，即Zii=Zero。

将该产业所有来自国外的中间品投入加总，作为，则：

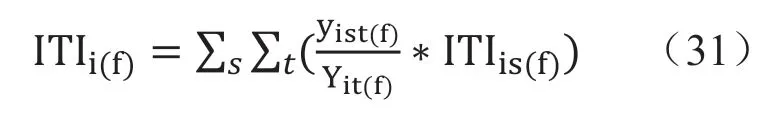
其中，角标f表示与国外产品转移有关，因而ITIi（f）表示i 国在基期和报告期之间的国外产业转移指数。

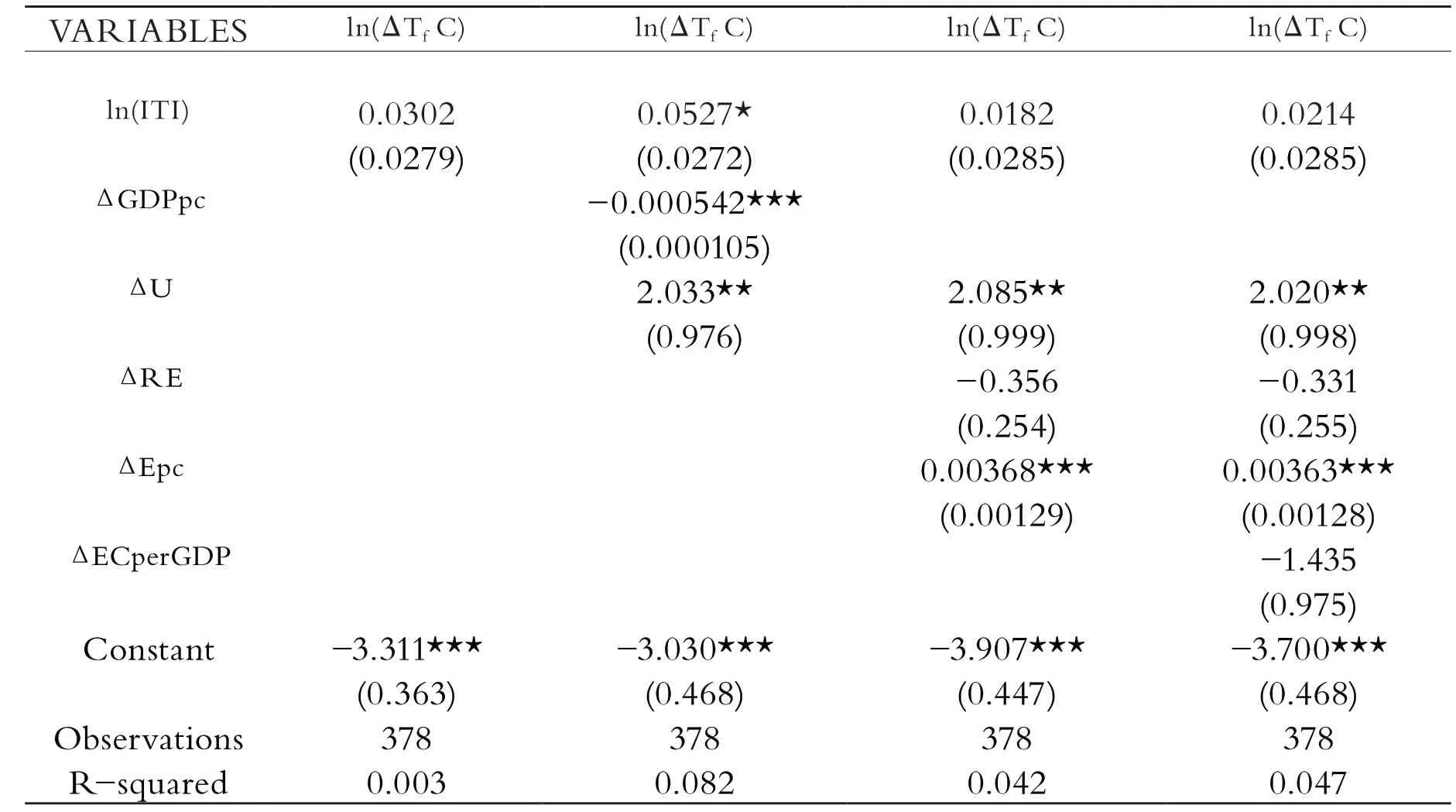
表8 第三次稳健性检验

将计算得出的国外产业转移指数代替原指数进行计量回归。因变量为国外需求拉动的碳排放变化量，结果如上表8所示。结果显示：虽然国外产业转移指数的系数转变为正值，然而其在多次回归中都不显著。这说明，当国内产业转移按照上述模型剔除后，国外需求对国内碳排放的影响并不显著。另外，城市化和人均耗电量则对碳排放有显著的正向影响。

六、结语

本文旨在探索国际间产业转移对本国由国外因素引起碳排放变化量的影响，选取世界各国2000-2009年相关数据，将多区域投入产出模型和结构分解法相结合，以动态视角计算九个时段内各国数据的变化情况，并通过计量模型进行回归分析。通过实证研究，本文得到以下结论：一是国际间产业转移确实会对产业接收国中由国外因素拉动的碳排放产生显著影响。当国内产业发展和转移因素被纳入考虑时，国际间产业转移会对各国由国外需求因素而导致的碳排放增量产生抑制作用，这一结论对“污染避难所”这一理论进行了驳斥；二是产业转移在发达国家对碳排放的影响并没有在发展中国家那样凸显。在本文的模型计算下，在发展中国家国外因素对碳排放量的影响程度要比在发达国家高出约30%；三是在国际间产业转移所带来的影响中，国外技术因素对碳排放增量的抑制作用比之需求因素更为显著，印证了“技术溢出效应”的存在。

有选择的引入国外产业，对有效减少国内碳排放有积极作用。同时，作为发展中国家，我国碳排放量对国际产业转移较为敏感，因此，对国际产业转移应持谨慎态度，鼓励高技术、低能耗的产业引进，将会有利于控制我国的环境污染状况、遏制碳排放增势。