基于小波自适应阈值的心音信号降噪方法
张宇宁

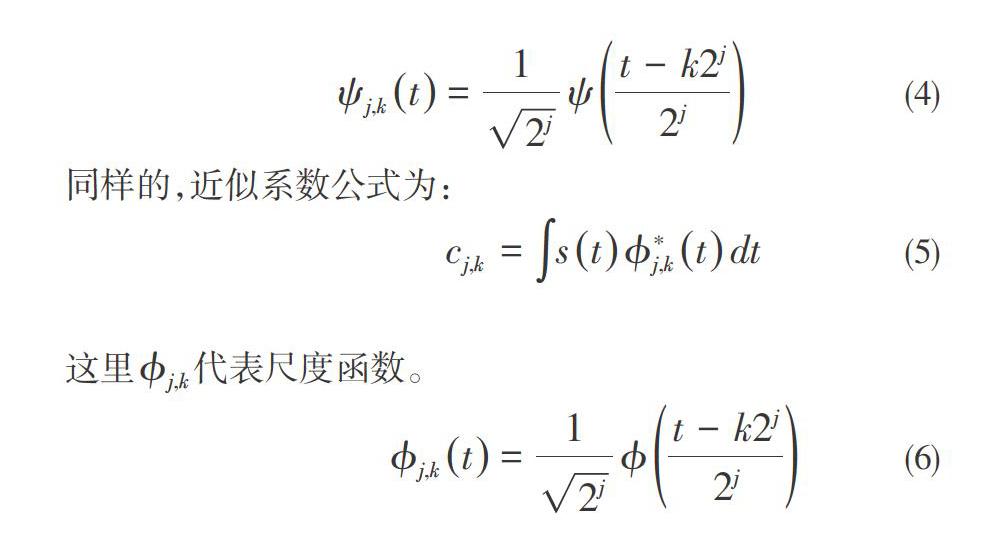
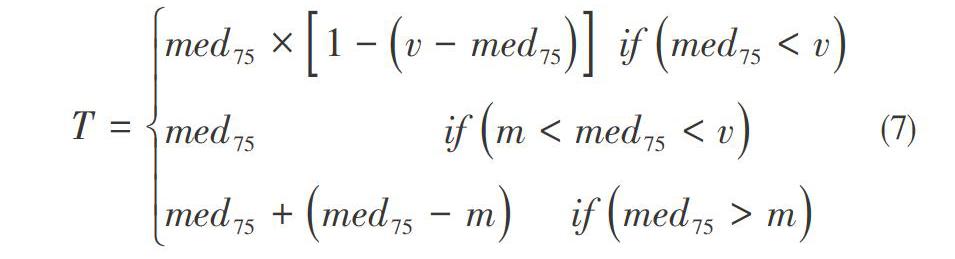
摘 要:心音信号作为人体最重要的生理信号之一,含有关于心脏状态的大量病理信息,然而在采集过程中,难免会被噪声影响,如被采集者本身的动作产生的噪音以及一些心脏的病理性噪音等。传统的小波阈值去噪方法,去噪效果并不理想。为了改善传统去噪方法出现的问题,拟用基于小波变化的自适应阈值心音去噪方法,并将效果与原始心音进行对比,结果显示该方法比传统方法去噪效果更好。
关键词: 心音去噪; 小波变换; 自适应阈值
中图分类号:TN912.3 文献标识码:A
文章编号:1009-3044(2021)03-0209-02
1 引 言
心脏疾病目前是造成健康问题的最主要的疾病,全球致死率达到30%,心脏疾病的早期诊断具有重要的意义[1]。心音检测具有无创的特点,心音信号包括心脏的各部分状态以及一些病理性信息,因而可以通过对心音的分析对心脏疾病进行检测。心音信号在采集的过程中,容易受到外部环境和人体自身运动等因素影响,进而影响到心音分析诊断的结果,所以心音信号的去噪尤为重要。本文主要应用一种在软阈值函数的基础上进行改进的自适应阈值和阈值函数,以原始心音信号为研究对象,选用coif5小波并进行5层离散小波分解,分别选用硬阈值函数、软阈值函数、中值函数、非线性中值函数等不同的去噪处理方法,并将去噪后的信号与原始信号进行对比,对于去噪心音信号信噪比(SNR)和均方差(RMSE)进行了数据分析。
2 心音信号的去噪
2.1 离散小波阈值去噪原理
离散小波变换对信号进行处理时,信号通过两个滤波器(高通滤波器、低通滤波器)分别得到细节系数和近似系数。再对近似系数进行进一步分解,得到二级的细节系数和近似系数。以此类推,可以得到预设级数的细节系数和近似系數。再由处理后的小波系数,重组得到去噪后的心音信号。
2.2 阈值的确定
为了更好地去除噪声,使有用的心音的成分损失较小,可以根据信号本身的特征来确定阈值,通过心音信号时域的信息来确定噪声的等级。Ann.Biomed[2]对于心音信号时域分析的方法中提到,在一个心动周期中,S1和S2的持续时间的总和不超过心音周期时间的25%,因此,利用小波分解后得到的小波系数进行排序,排序后数值总数75%的值代表信号中噪声的等级。这里引入一个新的变量[med75]代表系数矩阵的75百分位的值。
通过分析小波系数的均值、方差以及75百分位值的数值大小规律,将噪声分为低、中和高三个等级。当[med75]小于均值和方差时,噪声处于低等级;当[med75]大于方差小于均值时,噪声处于中间等级;当[med75]大于均值和方差时,噪声处于高等级,阈值应相应变大。根据三者之间的关系,阈值可以通过下面的公式确定:
2.3 阈值函数的选用
阈值确定后,应用阈值函数和确定的阈值对小波系数进行处理,传统小波阈值去噪的阈值函数有软阈值函数和硬阈值函数,硬阈值函数处理后的信号信噪比数值(SNR)大于软阈值函数,但是硬阈值函数可能会导致降噪后的信号失真等问题。为了改善这些缺陷,应用中值阈值函数[3]以及非线性中值阈值函数对心音信号进行处理,并且使用双阈值([T1]和[T2])对小波系数进行过滤,[T1]和[T2]由以下公式给出:
这个阈值函数延续了软阈值函数对于大于阈值部分的值进行保留的特点,并在此基础上减少了线性突变所产生的不连续的现象。
2.4 心音信号的重组
小波系数经过阈值和阈值函数处理后,对于处理后的小波系数进行信号的重组。重组过程为,对高级数的细节系数和近似系数进行升采样并通过合成的高通和低通滤波器,把滤波器的输出相加作为近似系数,重复进行下一级的重组。由于心音信号的特点,S1与S2的频率范围集中在25-120Hz,细节系数的五层分解的频率段为250-500,125-250,62.5-12.5,31.25-62.5,15.56-31.25Hz,我们选择对于第四层和第五层处理后的细节系数进行重组。
3 实验结果及讨论
3.1 数据的来源
实验使用的数据来自PhysioNet/CinC Challenge 2016,采样率为2KHZ,量化值位数为16bit,以WAV格式进行保存。为了验证非线性半软阈值函数的去噪效果,在原始的心音信号上加入高斯白噪声,信噪比(SNR)为10dB,采用coif5小波进行5层小波分解,分别比较硬阈值函数、软阈值函数、中值阈值函数和非线性中值阈值函数等不同的去噪方法,去噪效果如图1所示。
图1所示,(a)为采集到含噪的原始心音信号,图1(b)在图1(a)的基础上加入了高斯白噪声,噪声对于信号产生了很大的干扰。图1(c)是传统的硬阈值函数对含噪的心音信号进行去噪后的图形,可以明显看出存在较大的噪声。图1(d)是软阈值函数对含噪的心音信号进行去噪后的图形,与硬阈值相比,去噪效果更加明显,但是一些细节特征也被去除了。图1(e)和(f)是中值函数和非线性中值函数对含噪的心音信号进行去噪处理,可以看出这两种方法比硬阈值函数去噪效果更加明显,与软阈值函数相比,更好的重组出基础的心音。
3.2 阈值函数性能分析
为了更好地了解不同的阈值函数对原始心音信号去噪后的效果,本文选取信噪比(SNR)和均方根误差(RMSE)为评价指标[4],计算结果如表1所示。
由表1可知,非线性中值阈值函数的去噪后的心音信号的信噪比更大,即噪声含量更少,且均方差最小,具有较好的去噪效果。
4 结论
传统的去噪方法处理心音信号后,重构的信号仍然存在震荡,一些细节信息也被平滑掉。而自适应性的非线性阈值函数可以很好地去除噪声,去噪效果较为显著,且很好地保留了心音的细节信息。但是此方法仍然存在一定的缺陷,虽然对于细节信息的恢复相较于软阈值函数有了很大的进步,仍然会丢失掉一些细节信息。
参考文献:
[1] Singh J,Anand R S.Computer aided analysis of phonocardiogram[J].Journal of Medical Engineering & Technology,2007,31(5):319-323.
[2] 周克良,邢素林,聂丛楠.基于自适应阈值小波变换的心音去噪方法[J].广西师范大学学报(自然科学版),2016,34(1):19-25.
【通联编辑:闻翔军】

