定频化VIENNA整流器模型预测电流控制

韩会山，靳晨聪，毕艳军

（邢台职业技术学院电气工程系，河北邢台054000）

VIENNA整流器是一种高性能三电平整流器，凭借其电路结构简单、功率器件少、三电平特性的优点，在工业场合，尤其是对网侧电流质量要求高的场合应用十分广泛[1-4]。目前，VIENNA整流器已经被广泛应用于充电桩、通信电源以及电机驱动等对功率密度要求较高的场合[5]。

目前，国内外学者针对VIENNA整流器的闭环控制已经进行了很多研究，控制方法已由传统的线性控制发展至非线性控制[6]，例如无源型控制[7]、滑模控制[8]等。但这些方法设计较为复杂，不利于控制系统的实现。模型预测控制（model predictive control，MPC）作为一种新型的非线性控制方法，由于其原理简单、适用于非线性系统、以及易于控制多个约束目标的优点，非常适合于电力电子变换器的控制[9-10]，而其中模型预测电流控制（model predictive current control，MPCC）由于其对电流的直接控制，非常适合于VIENNA整流器。

目前MPC已经开始被应用于VIENNA整流器当中，文献[11]对VIENNA整流器数学模型进行了建立，并将有限集模型预测控制引入到了VIENNA整流器系统控制中，但是其电流给定设计复杂，且开关频率不固定，控制性能较差。文献[12]提出了一种基于离散空间矢量调制的模型预测控制方法，这种方法虽然可以固定开关频率，但是其计算复杂，不利于控制系统的设计。文献[13]采用了一种预测控制与滑模控制相结合的滑模预测直接功率控制，这种方法虽然可以对输入有功、无功进行有效控制，但对输入电流控制效果较差，并且这种混合控制方法的控制器设计较为复杂。

针对应用于VIENNA整流器的MPC开关频率不固定、设计较为复杂等问题，本文首先将传统MPCC方法引入VIENNA整流器控制中，然后通过对价值函数进行优化，同时引入调制模块，实现了预测电流控制的定频化。通过实验验证了所提方案的正确性与可靠性。

1 系统模型

VIENNA整流器的电路拓扑结构如图1所示，主要由输入滤波电感、三相整流桥、双向功率桥臂以及直流滤波电容组成，不控整流桥承担大部分功率。由于直流侧中点钳位的作用，输入侧体现三电平特征。

图1 VIENNA整流器电路拓扑Fig.1 Topology of VIENNA rectifier

结合图1所示的电路拓扑，由基尔霍夫定律可以得到在ab c坐标系下的系统回路方程如下式：

式中：ia，ib，ic为三相输入电流；Ua，Ub，Uc为三相输入电压；Uao，Ubo，Uco为交流侧桥臂中点与直流中点之间的电压；Ls为滤波电感；uoN为直流中点与交流侧中性点之间的电压；R为输入等效电阻。

在ab c坐标系下系统三相之间有耦合，不利于MPC的实现，对此将系统数学模型转换至α-β坐标系下，转换矩阵如下式所示：

设VIANNA整流器的输入桥臂中点的电压为UaN，UbN，UcN，据此可得在α-β坐标系下系统数学模型如下：

VIENNA整流器属于三相三电平拓扑，但是由于其结构是一种单向Boost型的，因此其零电压矢量输出有限，故其只能产生25种电压矢量。VIENNA整流器的空间电压矢量与开关状态对应的分布图如图2所示。

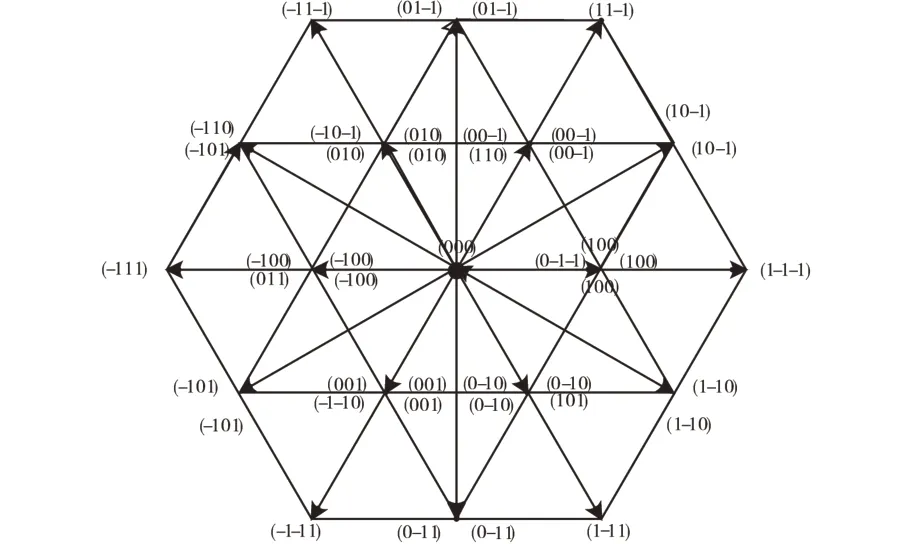
图2 空间矢量分布图Fig.2 Space vector distribution diagram

2 传统模型预测电流控制

首先，为了得到系统的离散数学模型，需要对原有数学模型离散化，常采用一阶前向欧拉法对模型进行离散化，采用的离散表达式如下：

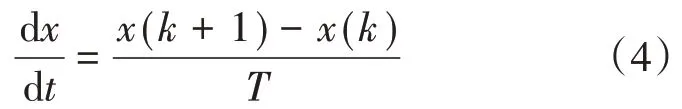
根据式（3）所示的数学模型，采用式（4）所示的离散化方法，可获得如下式所示的系统在α-β坐标系下的离散化数学模型：

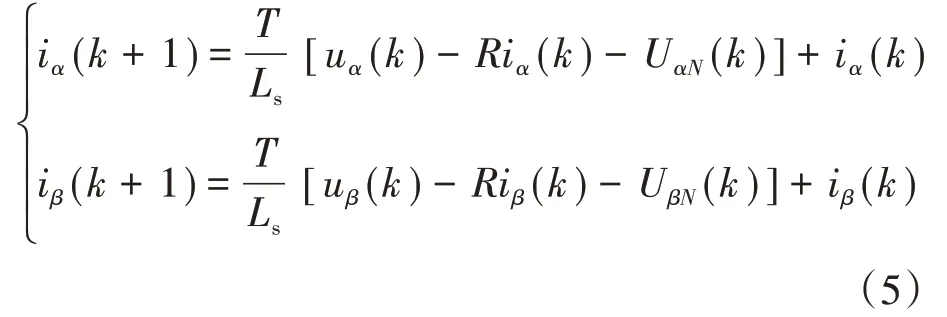
式中：iα,β(k+1)分别为输入电流在α轴和β轴的分量；uα,β(k+1)分别为输入电压在α轴和β轴的分量；uαN(k),uβN(k)为桥臂输入电压在α轴和β轴的分量。

式（5）就是VIENNA整流器的电流预测模型。

根据系统控制目标，以预测电流与参考电流差的平方作为价值函数用于评价候选矢量，构建的价值函数表达式如下：

在获得VIENNA整流器的离散数学模型之后，将图2中所示的25种电压矢量分别代入预测模型中，获得相应的预测电流，再根据价值函数选出最优电压矢量，将此矢量对应的开关状态输出作用于变换器。传统模型预测控制实现流程图如图3所示。

图3 MPC实现流程图Fig.3 Flow diagram of MPC

3 定频化MPC

传统的MPC存在计算复杂，开关频率不固定的缺点，这阻碍了模型预测控制在VIENNA整流器中的应用，因此本节提出了一种优化算法固定开关频率。

首先，将式（5）所示的系统离散数学模型转换至d-q坐标系下，用于转换的矩阵如下式所示：

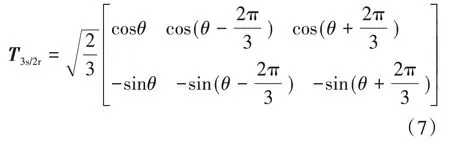
式中：θ为阻抗角，单位rad。

将式（5）与式（7）相乘进行转换，经坐标转换后的系统预测模型如下式所示：

式中：id,q(k+1)为预测电流在d，q轴下的分量；ud,q(k)为输入电压在d，q轴下的分量；id,q(k)输入电流在d，q轴下的分量；Ud,q(k)为桥臂电压在d，q轴下的分量；ω为角频率，单位rad/s。式（8）就是d-q坐标系的预测模型。此时，重新定义d，q轴下的价值函数如下式：

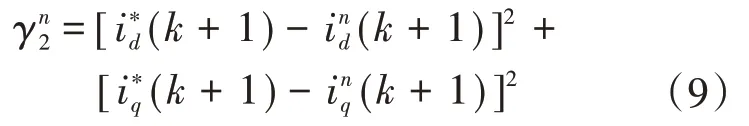
令k+1时刻参考电流值和预测值相等，有：

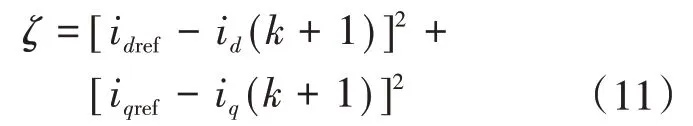
为了将式（11）中的未知量用已知量表示，结合式（8）和式（11）可以得到如下表达式：

对其求偏导，且令偏导数为零，可得：

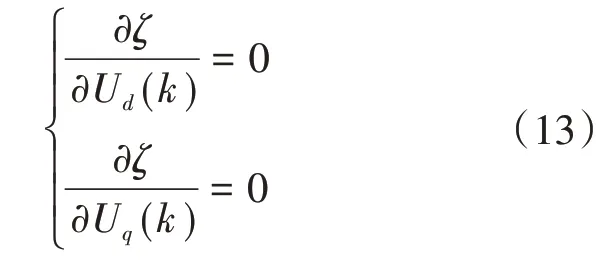
由上可得k时刻桥臂电压参考值如下：

图4 实现框图Fig.4 Realization block diagram

4 实验结果

为了验证本文所提方案的正确性，搭建了以ARM为控制核心的实验平台，试验参数为：直流母线电压200 V，直流侧C1=C2=1 500μF，滤波参数L1=10 mH，采样频率10 kHz，电网电压100 V/50 Hz，输出功率Po=500 W。

图5为在传统MPC控制下的VIENNA整流器稳态运行时的波形。从图5a可以看出，此时系统输出电压稳定在200 V左右，同时，输入电压电流相位相同，此时，输入电流正弦，但输入电流纹波较大；从图5b所示的输入电流FFT可知，此时输入电流THD＞5%，不满足并网电流的要求。

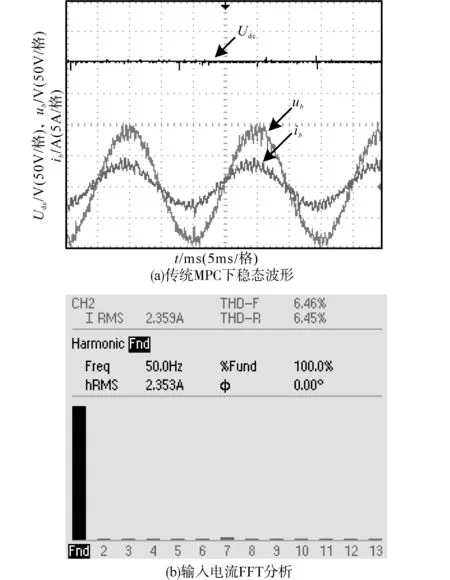
图5 传统MPC下VIENNA整流器稳态波形Fig.5 Steady-state waveforms of VIENNA rectifier under conventional MPC

图6为采用传统MPC控制方法下的系统动态波形。图6a为系统负载由100%Po突变为60%Po时系统的动态波形；图6b为系统负载由60%Po突变为100%Po时系统的动态波形。可以看出，在传统MPC控制下，不论在负载突增还是突减情况下，输出电压都可以快速跟踪给定。

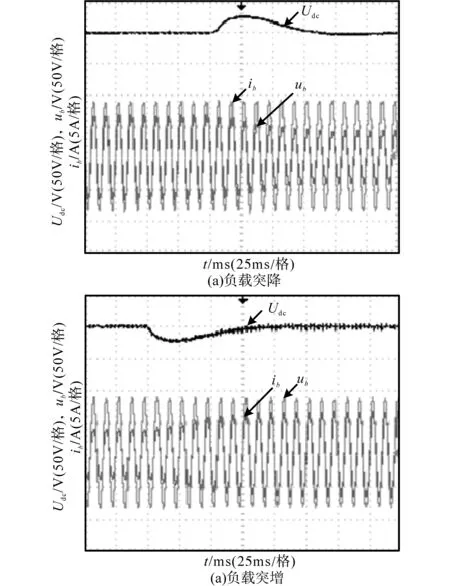
图6 传统MPC下负载突变时系统稳态波形Fig.6 System steady-state waveforms when load is abrupt under conventional MPC

图7为采用定频化预测控制下的VIENNA整流器稳态实验波形。从图7a中可以看出，此时系统输出电压稳定在200 V左右，同时，输入电压电流同相位，此时，输入电流正弦，且纹波很小，从图7b所示的输入电流FFT可知，此时输入电流THD＜5%，满足并网要求。

图8为采用定频化MPC控制方法下的系统动态波形。图8a为系统负载由100%Po突变为60%Po时系统的动态波形；图8b为系统负载由60%Po突变为100%Po时系统的动态波形。从图中可以看出，无论系统负载突增还是突减，在很短时间后系统会重新恢复稳定，输出电压可稳定在给定附近，系统具有良好的动态性能。对比图6与图8可以发现，定频化MPC基本可以实现与传统MPC一样的动态控制性能，这说明了定频化MPC在提高稳态控制性能的同时，动态性能也保持良好。

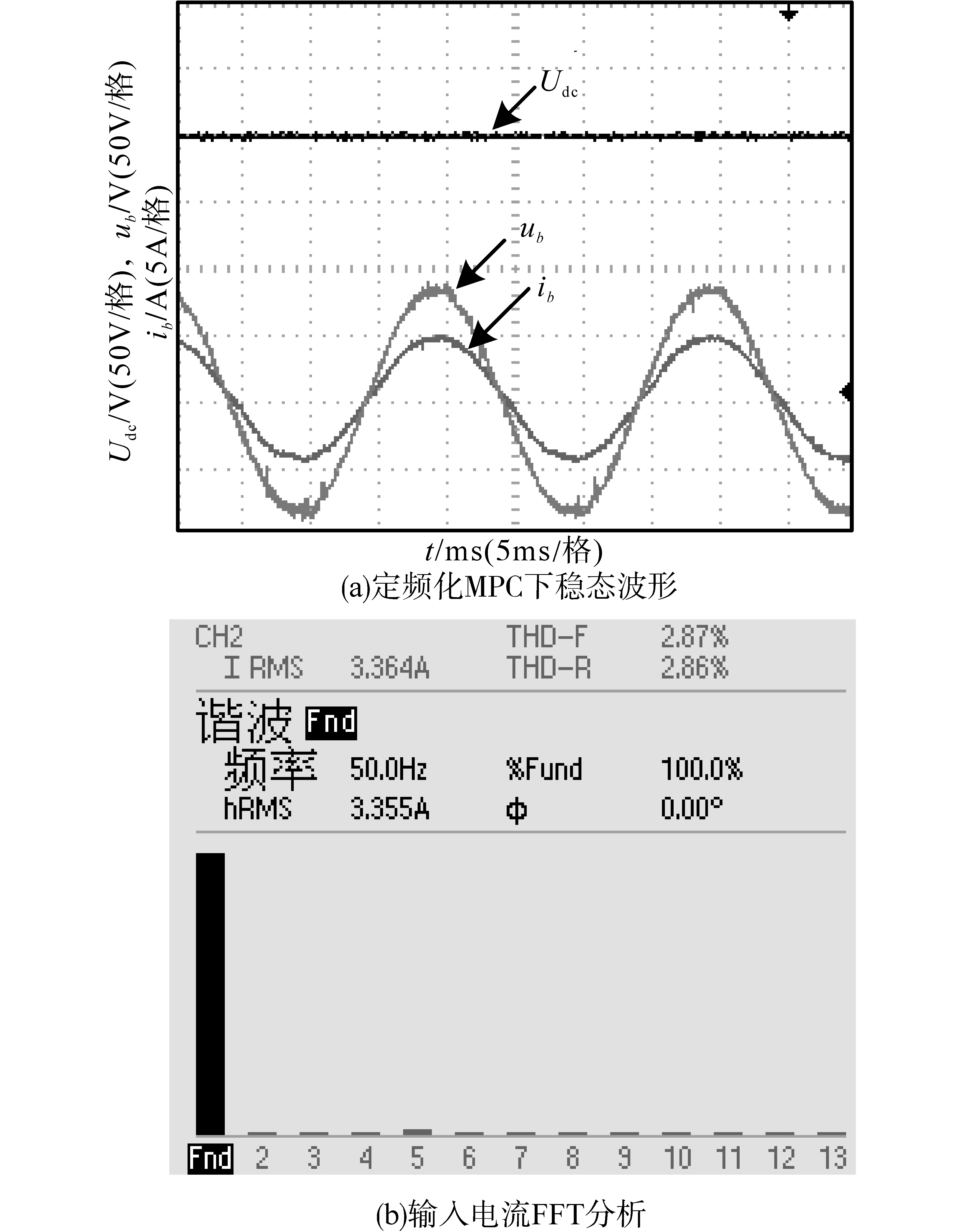
图7 定频化MPC下稳态波形Fig.7 Steady-state waveforms under fixed-frequency MPC

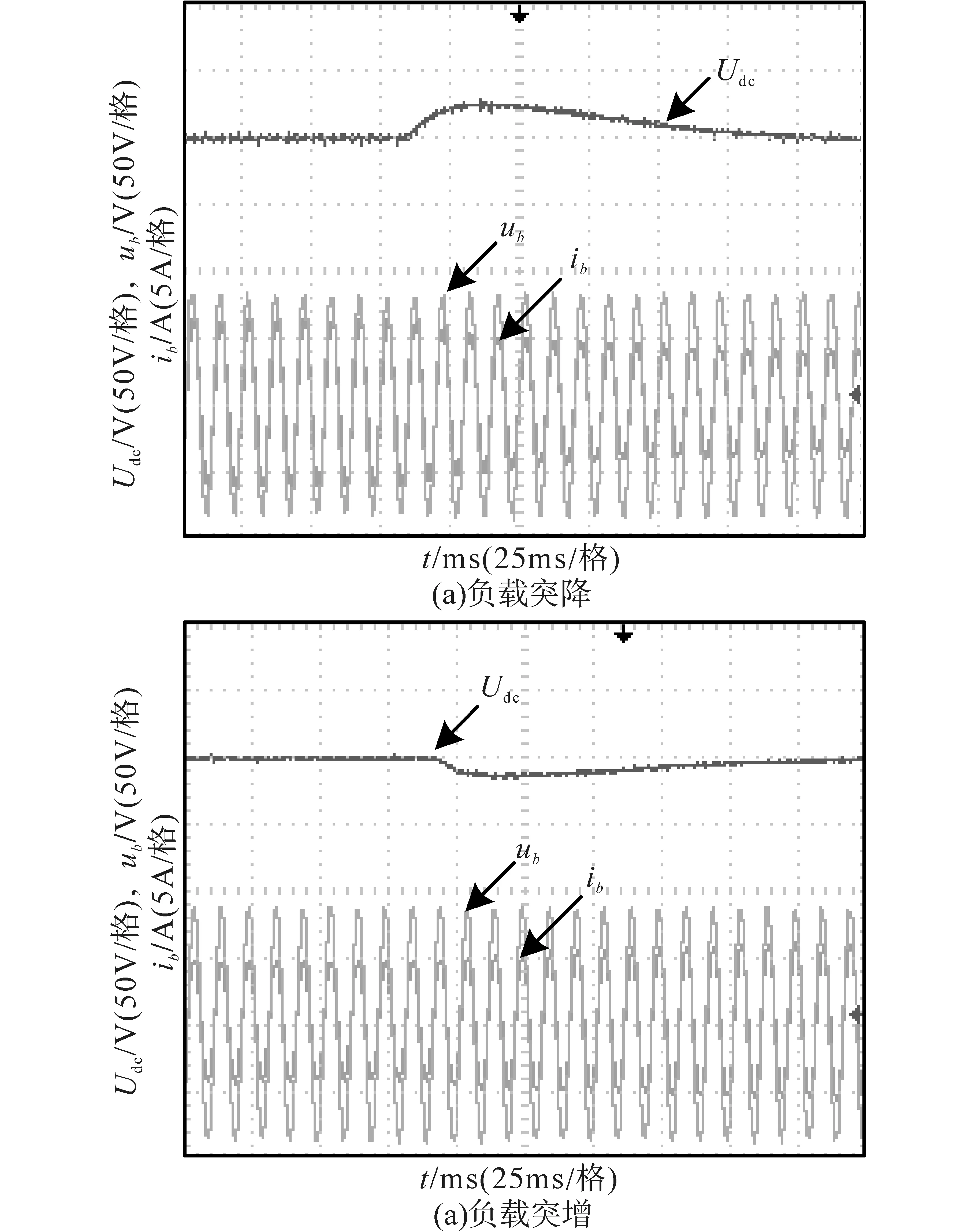
图8 定频化MPC下负载突变时系统稳态波形Fig.8 System steady-state waveforms when load is abrupt under fix-frequency MPC

5 结论

本文将MPC引入到了VIENNA整流器的控制中，并针对传统MPC开关频率不固定的缺点提出了一种定频化MPC方法，通过引入d-q坐标系下离散数学模型，并进行价值函数优化，预测出新的调制信号，用过SPWM调制使开关频率固定，优化系统控制性能。通过搭建实验样机，利用实验证明了所提方法能有效改善系统控制性能。