基于高转矩电流比的开关磁阻电机DITC优化控制

许爱德，黄乐鹏，李倩妮，商超亿，朱景伟

（1.大连海事大学信息科学技术学院，辽宁大连116026；2.大连海事大学船舶电气工程学院，辽宁大连116026）

开关磁阻电机（switched reluctance motor，SRM）作为一种新型调速电机，相对于异步电机、永磁同步电机，具有结构简单、成本低、启动转矩大、功率电路简单可靠、效率高等一系列的优点，引起国内外学者的普遍关注与深入研究[1]。但由于其本体的双凸极结构以及电磁关系的高度非线性，存在转矩脉动过大、电机模型不精确等问题，限制了其高效特性和在低转矩脉动场合中的应用。

在开关磁阻电机调速系统中，转矩控制方法可大致分为2种：间接转矩控制和直接转矩控制（direct torque control，DTC）。间接转矩控制一般使用转矩分配函数（torque sharing fuction，TSF），大都需要存储大量的非线性特性数据去完成准确的转矩电流转换。

直接转矩控制可以克服部分间接转矩方法的缺点。文献[2-3]提出了一种在线控制的直接瞬时转矩控制方法。直接瞬时转矩控制（direct instantaneous torque control，DITC）根据实时转子位置，对单相导通区和两相同时导通的重叠区域分别制定不同的滞环控制规则，通过滞环控制规则直接选取开关矢量输出到功率变换器。文献[4-7]对比分析了TSF，DTC和DITC控制策略，并表明DITC比DTC和TSF效率更高、响应更快、更容易实现。但是，DITC在交叠区需要复杂的导通规则来产生平滑的转矩，同时在电流上升初期电流峰值过高，会出现转矩脉动过大，转矩电流比低的现象。文献[8]提出一种电流软斩波，分段脉宽调制（pulse width modulation，PWM）变占空比的控制，拟合了占空比和转速、参考电流的函数关系式，达到了电流优化的控制效果。文献[9]提出了一种结合DITC和脉宽调制的控制方法，对每相电压占空比进行实时调整，但是占空比的选取跟电机本体参数联系密切，不容易实现且没有体现负载对占空比的影响。

针对上述问题，结合分段变占空比调制思想，本文提出了一种改进的直接瞬时转矩控制策略，即，脉宽调制-直接瞬时转矩控制（PWMDITC）。拟合出占空比-转速-负载函数关系式，获得最优的电压矢量，通过分析得到1个电周期中转矩电流比最大的点，以此对交叠区进行扇区细分并进行导通规则优化。在仿真和实验中对优化控制策略进行验证。

1 DITC控制策略

1.1 开关磁阻电机转矩计算

根据基尔霍夫电压定律，SRM的单相瞬时电压表示为

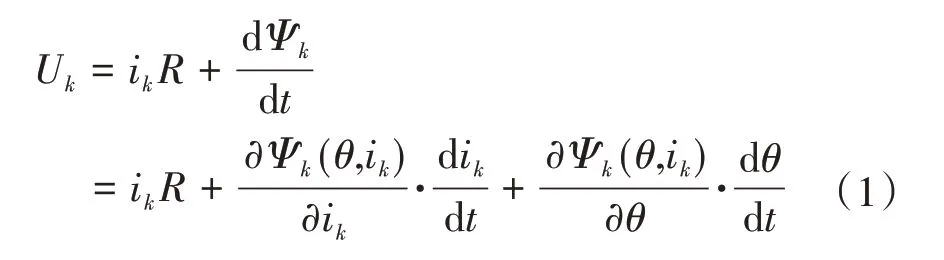
式中：k为相数，k=1，2，3；Uk为第k相电压；ik为第k相电流；R为电机绕组阻抗；Ψk(θ,ik)为第k相磁链，是相电流ik和转子位置角θ的函数。

在开关磁阻电机中，转矩通常根据磁共能进行计算，一般计算公式表示如下：

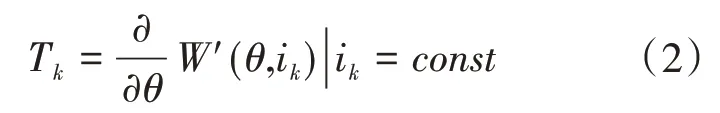
式中：Tk为第k相的瞬时转矩；W′(θ,ik)为磁共能。磁共能由下式表示：

由式（3）可知，磁共能是关于位置角和相电流的函数。Lk(θ,ik)为第k相电感。当忽略磁饱和效应时，Lk(θ,ik)可简化为与相电流无关的函数Lk(θ)，在线性电感模型下相转矩和合成转矩可表示为

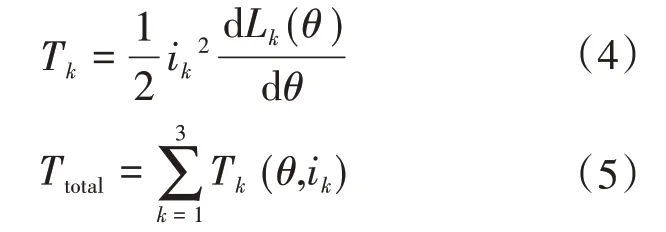
1.2 DITC控制原理

DITC控制框图如图1所示，参考转矩和实际转矩的误差通过滞环产生开关信号。实时转矩通过滞环的内环和外环调节。换相时的状态如图2所示，在单相导通区，励磁相产生电机所需要的转矩，通过内环调节；在交叠区，励磁相和退磁相共同承担产生转矩的责任，分别通过内环和外环调节转矩。但是在励磁相刚导通时，电感变化率比较小，为了产生所需的转矩，会出现一个较大的电流峰值且转矩也会有一个向上的脉动。

图1 传统DITC控制框图Fig.1 Block diagram of the traditional DITC

图2 SRM不同运行区间示意图Fig.2 Schematic diagram of different operation intervals

在传统DITC中，开通角对其影响很大，可以通过优化开通角将DITC的脉动控制在一定范围内，但是电流上升初期的峰值不可避免。在对齐位置附近，大的电流峰值也增加了震动和噪声。固定的开通角、关断角也不能适应全速，对于不同的工况，相应的最佳开通角、关断角并不相同。不同的开通角、关断角也影响着交叠区的大小，交叠区中各相转矩的状态与电机的合成转矩脉动密切相关。本文在优化了开通角的基础上，重新划分扇区，通过对交叠区与单相导通区施加不同的占空比对转矩实现更精确的控制。

1.3 开关状态

功率变换器采用三相不对称半桥结构，开关状态有3种，如图3所示。

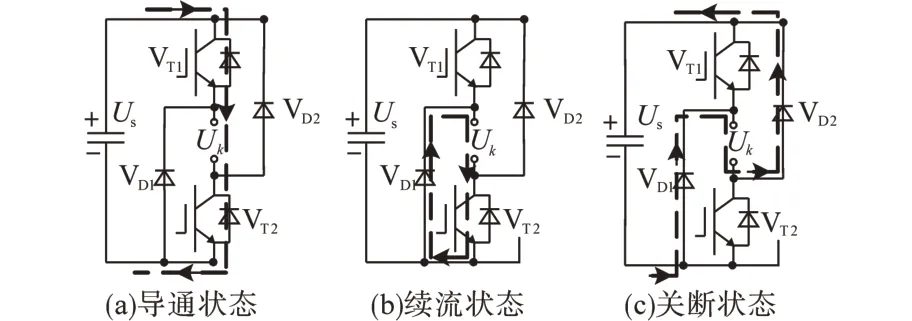
图3 SRM功率变换器开关模式Fig.3 State diagrams of SRM power converter

当忽略绕组阻抗，UT，UD表示开关器件和二极管的压降。相电压在三种开关状态下可表示为

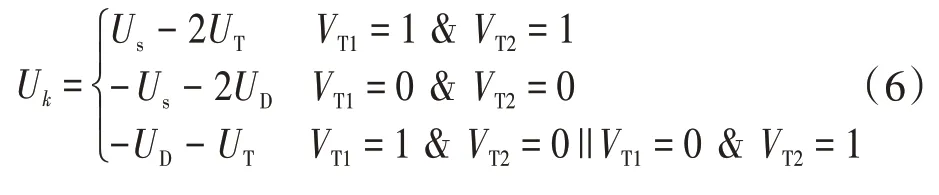
2 DITC优化控制策略

2.1结合PWM的DITC控制策略

当忽略绕组压降，式（1）可改写为

整理式（7）可得：

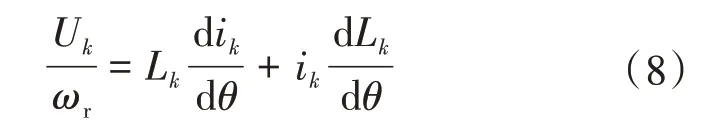
式中：ωr为转子转速。

在线性电感模型下，电感斜率变化点记作θ1u，从开通角θon到θ1u期间，认为L=Lmin，i(θon)=0，可得：

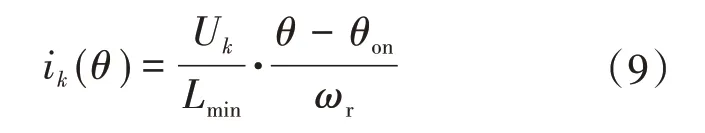
电流变化率为

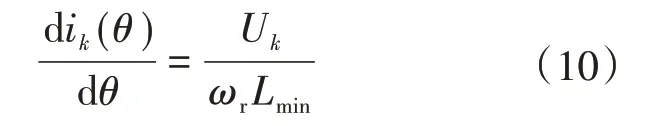
由式（9）、式（10）可知，电流在θ1u处达到最大，电流变化率与转速成反比。当转速上升，相电流变化率下降，电流跟踪能力减弱[10]。当负载增加时，为了提供足够的转矩，需要获得足够大的电流，尖峰电流值将会增大。由以上分析可知，不同负载、转速下，需要为各相提供合适的相电压。在传统DITC中，1个控制周期只有1种开关状态，在低速或小负载工况下，存在电压矢量作用时间过长的问题。对此，可以结合PWM调制技术，对开关管施加合适的占空比。PWMDITC的控制框图如图4所示。

图4 PWM-DITC的控制框图Fig.4 Block diagram of PWM-DITC

2.2 基于最大转矩电流比的扇区划分

最大转矩电流比控制（maximum torque per ampere，MTPA）意味着电机产生的转矩与定子相电流之比达到最大值。在这种情况中，电机在输出转矩不变的前提下，消耗的定子电流更小，实现了能量优化，提高了电机的效率[11]。一个电周期下的平均转矩可由下式表示：

电流均方根值由下式表示：

转矩电流比（torque per ampere，TPA）的定义由下式表示：

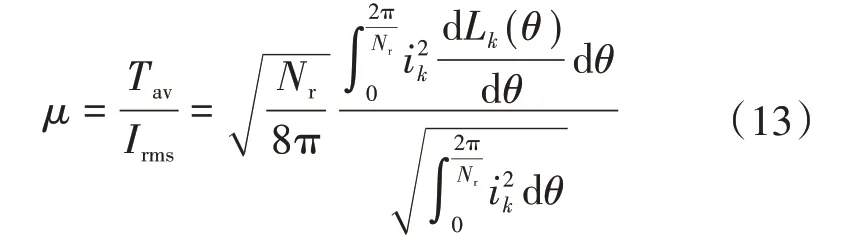
式中：Nr为转子极对数。

在电感线性区，d Lk(θ)/d(θ)为常数，非线性区电感斜率为零，由式（9）、式（13）可知，θ1u为转矩电流比最大的点。转矩电流比大代表着铜耗更小，在一定程度上也代表着效率更高。

θ1u是转矩电流比最大的点，也叫做临界重叠位置。电感在此之前非常小，电流上升很快，之后电感进入线性区，电感斜率最大，转矩迅速的建立起来。本文以作为θ1u划分点，在非线性电感模型下，将每相机械角划分为5个区域，如图5所示。以A相为例，Aon为A相开通角，Aoff为A相关断角，A1u为A相电感斜率变化点。

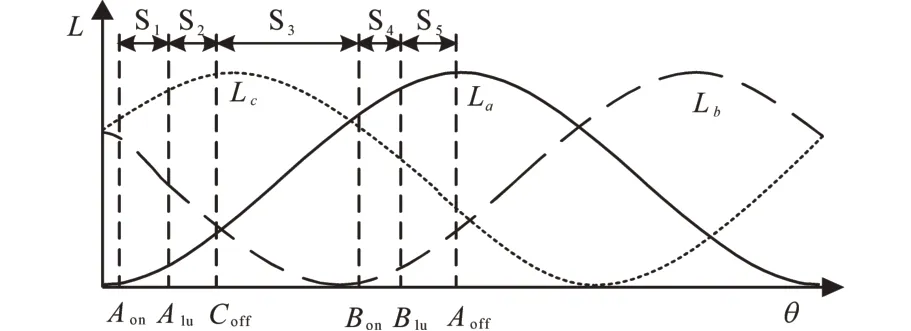
图5 区间划分Fig.5 Interval partition

2.3 导通规则与占空比调制

若开关磁阻电机运行时的三相绕组工作顺序为C→A→B→C。滞环带为[-TH,TH]，以A相为例进行说明。

S1区域：A相作为励磁相，刚导通时A相电感很小，电感变化率也几乎为零，能够提供的转矩很小，在该区域，转矩主要由C相提供。在转矩误差小于滞环下界时，ΔT≤-TH，给予A相关断。在转矩误差大于上界时，使其处于导通状态。

S2区域：A相电感仍然较小，但是电感变化率在不断增大，在该扇区转矩变化比较剧烈，在C相关断之前，转矩仍然需要由C相提供，误差在转矩滞环内时，使A相处于续流状态。

S3区域：该扇区是单相导通区，当转矩误差大小在转矩滞环内时，使A相导通，按照占空比公式确定占空比大小。在滞环带以外，使A相关断。

S4区域：此时A相将转变为退磁相。B相在刚导通时面临同样的情况，转矩主要由A相提供。

S5区域：在A相彻底关断，B相转矩建立之前，仍然给A相励磁，在B相转矩建立之后，使A相续流，在关断角之后，施加反压关断。

交叠区和单相导通区施加的占空比分别为α1，α2。其中，由仿真实验数据拟合获得，其表达式如下：

从式（14）、式（15）可知，当负载转矩小于7 N·m时，占空比是关于转速n的一次函数；当负载较大时，励磁状态下占空比随着转速和负载的增大而增大。

3 系统仿真与分析

本文在Matlab中将DITC与PWM-DITC进行仿真对比。对一台三相12/8极SRM进行仿真验证。为了对结果进行对比，定义纹波转矩的峰峰值ΔTpp与平均转矩Tav的比值为转矩脉动系数TRF[12]，如下式：

2.3 传统DITC仿真分析

仿真测试在Matlab/Simulink环境下进行，其中DITC的滞环宽度为0.2 N·m/0.25 N·m，给定负载转矩为5 N·m、转速800 r/min。图6为统一关断角下开通角分别在0°，2°下合成转矩与相电流波形。

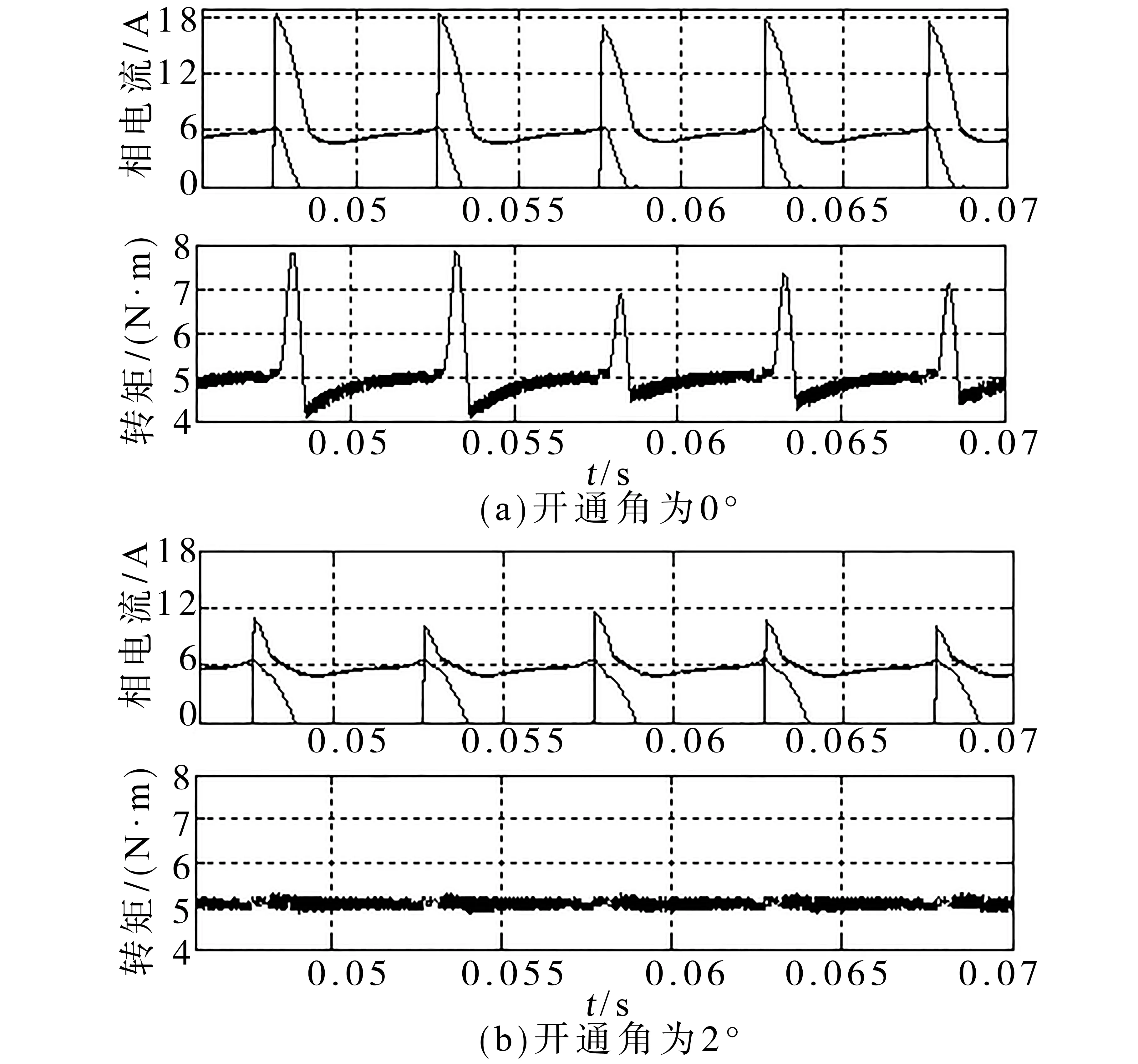
图6 不同开通角下的DITC仿真波形Fig.6 Simulation waveforms of DITC under different turn-on angles

由图6可知，不同的开通角对转矩和电流的波形影响很大，未经优化的开通角在交叠区产生一个向上的转矩脉动。

在相同的开通、关断角下，在800 r/min，10 N·m下，PWM-DITC与开通角优化后的DITC的电流和转矩的波形对比如图7所示。图8为DITC和PWM-DITC的磁链图对比。图9为不同转速、不同负载下DITC与PWM-DITC的转矩电流比折线图。

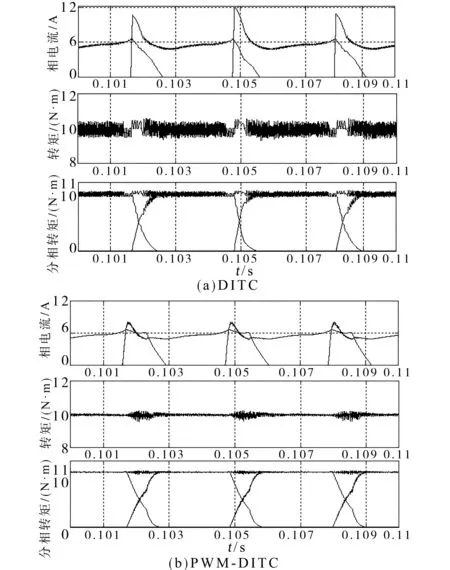
图7 800 r/min，10 N·m下，DITC与PWM-DITC运行曲线Fig.7 Simulation waveforms of DITC and PWM-DITC under 800 r/min and 10 N·m

由图7可知，通过分段变占空比调制，将电压矢量施加在重新划分的扇区上，可有效降低电流峰值，同时转矩脉动也进一步优化。DITC的峰值电流为12 A，PWM-DITC的峰值电流为7.8 A，峰值电流有明显的降低。DITC在稳态时的转矩脉动为

PWM-DITC在稳态时的转矩脉动为

由式（17）、式（18）可知，与经过开通角优化的DITC相比，转矩脉动仍然进一步优化。同时转矩电流比由式（13）计算可知，DITC在稳态时的转矩电流比为1.49，PWM-DITC的转矩电流比为1.53。

图8 DITC和PWM-DITC的磁链图对比Fig.8 Flux-linkage circle of DITC and PWM-DITC

由图9可知，PWM-DITC的转矩电流比大范围内都高于DITC，在中、低速效果最明显。也侧面契合了传统MTPA控制策略的特性，高速时优化并不明显，但是整体看来转矩电流比得到进一步优化。

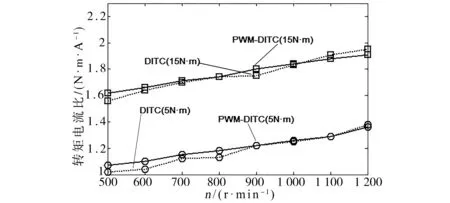
图9 不同转速、负载下转矩电流比Fig.9 Torque-current ratio under different speed and loads

4 实验结果及分析

为了验证PWM-DITC算法的有效性，本文以一台三相12/8极开关磁阻电机调速系统作为实验平台。平台主要包括功率变换器、DSP控制器、三相12/8开关磁阻电机、人机交互系统。采用转矩传感器测量转矩，使用磁粉制动器作为电机的负载。

图10a表示DITC的实验结果，图10b表示PWM-DITC的实验结果。由图10可知，传统DITC在换相时，刚导通相会出现较大的峰值电流，在12 A左右，并且随着负载的增大而急剧增大。PWM-DITC在导通初期仍然由上一相提供转矩。在励磁相转矩建立起来后，再由励磁相提供转矩，完成交叠区平稳的过渡。峰值电流降到了7 A左右，避免了导通初期励磁相电感小，电流变化快，造成电流峰值过大的问题。实验中DITC的转矩脉动为2.96 N·m，PWM-DITC的转矩脉动为2.04 N·m。在降低电流峰值的同时，转矩脉动也得到了优化。DITC的转矩电流比为1.48，PWM-DITC的转矩电流比为1.5。可知PWM-DITC可以有效地降低电流峰值和平均值，同时优化了转矩脉动，提高了转矩电流比，具有更高的效率。

3.2 PWM-DITC仿真分析

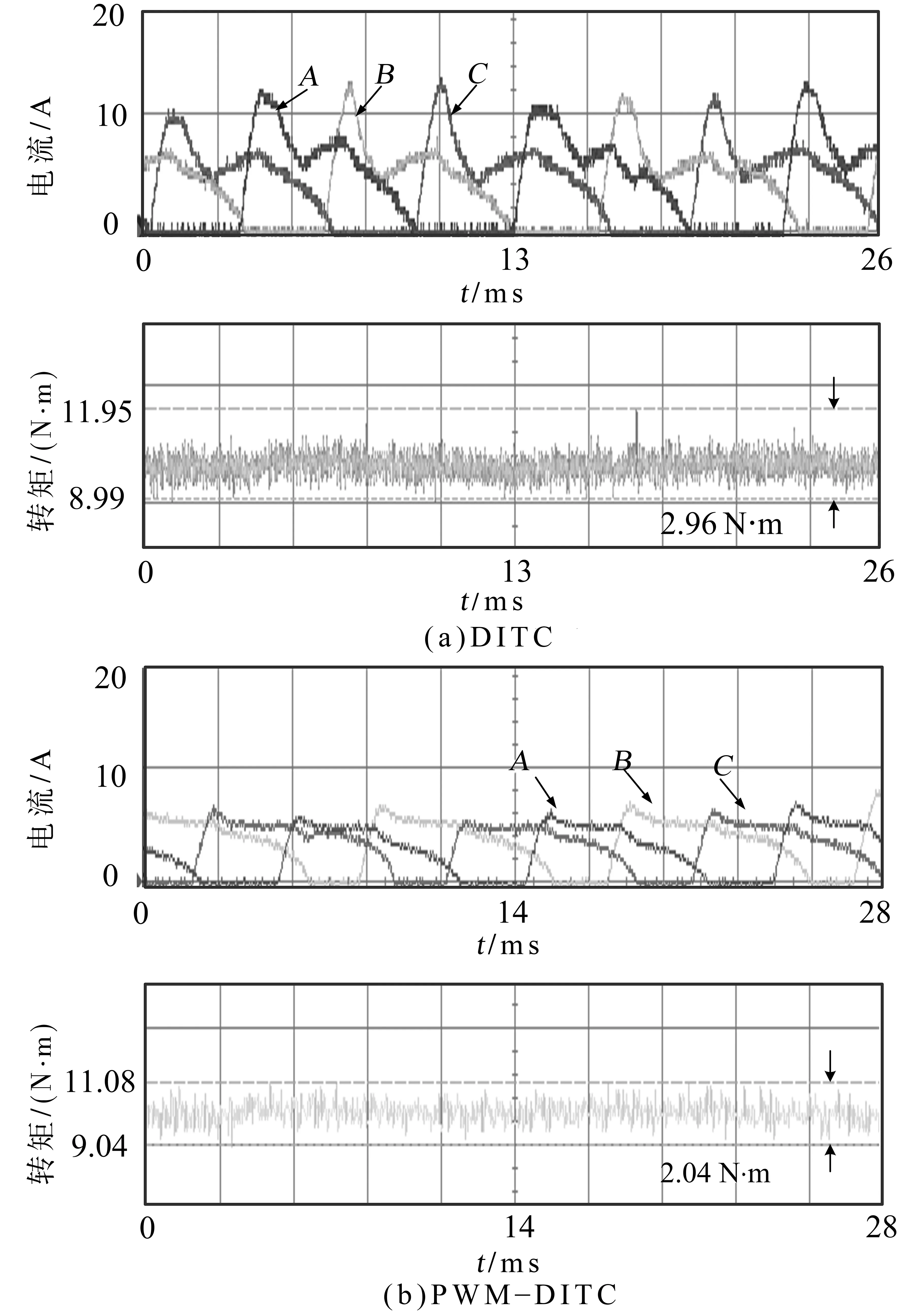
图10 在800 r/min，10 N·m下，DITC和PWM-DITC实验结果Fig.10 Experimental results of DITC and PWM-DITC（Constant speed at 800 r/min with 10 N·m load）

5 结论

本文针对传统DITC电流峰峰值高及交叠区脉动大，转矩电流比低的问题，分析了其产生的原因并且探究了开通角对转矩脉动和电流波形的影响，在优化了开通角的基础上，对DITC和PWMDITC进行对比分析。PWM-DITC根据电感斜率变化点对机械角进行扇区划分，并对导通规则进行优化，使用分段变占空比的方式调制出最优的电压矢量。在仿真和实验的基础上建立了占空比—转速—负载的函数关系式。在仿真和实验中验证了PWM-DITC的有效性，改善了电流波形，提高了算法在中、低速区间的转矩电流比，拓宽了采样周期，对转矩脉动也进一步优化。