基于改进幂次趋近律的Buck变换器滑模控制方法研究

姜文东，王海涛，张森海，葛黄徐，周赞东

（1.国网浙江省电力有限公司，浙江 杭州310007；2.国网电力科学研究院武汉南瑞有限责任公司，湖北武汉430074；3.国网浙江省电力公司嘉兴供电公司，浙江嘉兴314033）

随着人们生活水平和用电设备智能化的不断提高，对电能质量要求相应水涨船高，尤其高精密仪器设备对电能质量的要求更加严格。发电机组无法给所有用电设备提供合适的电压，此外，电能在输、变电过程中易出现损耗或受到噪音等因素的干扰，电能质量得不到保证。Buck变换器作为开关电源的核心部件，在体积、重量、能耗等方面具有一定优势，已广泛应用于工业仪器设备、计算机以及航空航天等领域[1-4]。

当前，Buck变换器通常采用PID控制算法，但当系统受到外部扰动或者内部参数变化时，Buck变换器会出现动态响应速度慢、输出波形谐波含量较高等缺点。滑模变结构控制算法对外部扰动以及内部参数变化具有极好的鲁棒性，动态性能优异，适宜于工程实现[5]。但算法自身存在局限性，在切换频率无法达到无限大前提下，系统会产生抖振。

为解决这一难题，文献[6]提出趋近律控制方法来减小滑模运动中的抖振问题；文献[7]针对传统趋近律收敛速度慢、抖振较大等缺点，提出一种双幂次趋近律控制方法，该方法克服了单幂次趋近律距离滑模面较近时，收敛速度放缓等缺点；文献[8]针对指数趋近律超调量大等缺点，提出一种基于模糊控制的趋近律方法，通过模糊控制自适应调节指数趋近律参数，有效提高系统收敛速度，减小抖振；文献[9]利用状态空间平均法，建立Buck变换器工作状态下的数学模型，通过建立基于多幂次趋近律的滑模控制器，实现对Buck变换器输出电压的精确控制。

本文在上述文献基础上，提出一种基于改进幂次趋近律的滑模控制方法，并将其应用于Buck变换器三阶滑模控制器。该控制方法不仅增强了系统的动态性能，而且随系统状态变化有效降低抖振大小，最终收敛于平衡点。

1 Buck变换器数学模型

Buck变换器又称直流降压变换器，是DC/DC变换器的一种，拓扑结构如图1所示。

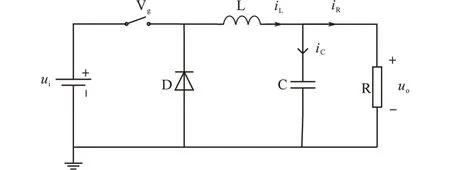
图1 Buck变换器拓扑结构Fig.1 Buck converter topology

图1中，ui为输入电压，uo为输出电压，Vg为开关管，D为二极管，C为电容，L为电感，R为电路负载。通过调节开关管Vg通断，实现控制输出电压uo的作用。具体来说，当开关管Vg闭合时，输入电压ui通过电感L给输出端供电，此时，二极管由于受到反向电压，处于关断状态。当开关管Vg关断时，由于电感L续流作用，电流不会立即下降为零。此时，二极管承受正向电流导通，负载电流通过二极管放电，起到降低电压uo大小的目的。

假设Buck变换器负载为线性负载，根据基尔霍夫定律，定义电感电流iL和输出电压uo为系统状态变量，求得Buck变换器状态空间方程为

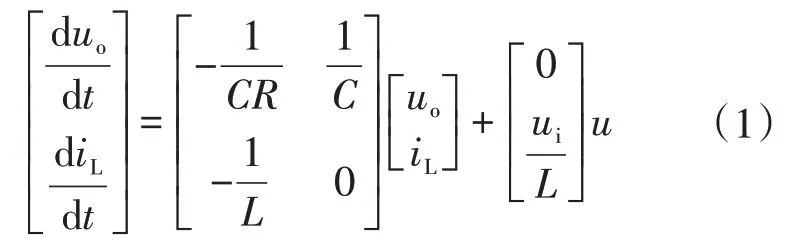
式中：iL为电感电流；u为开关管Vg通断，当u=1时，Vg闭合，当u=0时，Vg关断。

2 改进幂次趋近律控制方法

2.1 趋近律的提出

目前常用的趋近律有以下4种，如表1所示[10]。

表1 四种趋近律比较Tab.1 Comparison of four reaching laws

表1中，s˙为滑模趋近律；s为滑模面；k，ε为趋近律参数；sgn为符号函数。4种趋近律各有优缺点：等速趋近律的设计方法简单，趋近速度取决于参数ε。当参数ε较大时，系统状态能从较快的速度趋近滑模面，但到达滑模面后的抖振较大；当参数ε较小时，系统状态到达滑模面时间过长，且无论参数ε如何选择，系统状态均不能收敛于平衡点。相比于等速趋近律，指数趋近律具有更快的收敛速度，但系统状态仍不能收敛于平衡点。

幂次趋近律能够保证系统状态收敛于平衡点。当系统状态距离滑模面较远时，收敛速度较快，但当系统状态距离滑模面较近时，尤其 ||s＜1时，收敛速度极慢。变速趋近律同样能够保证系统状态最终收敛于平衡点。不同之处在于，变速趋近律滑模区域呈扇形，随系统状态变化渐近收敛至平衡点。当参数ε较大时，收敛速度较快，到达滑模面后状态x较大，导致系统抖振较大；当参数ε较小时，导致收敛速度缓慢，到达时间过长。

本文综合幂次趋近律和变速趋近律的优点，提出一种改进幂次趋近律，其数学表达式为

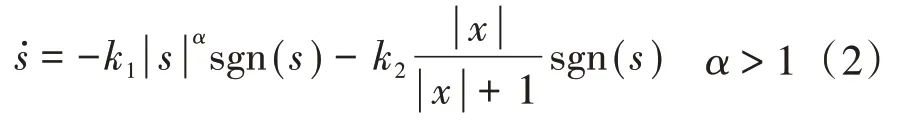
式中：k1，k2为趋近律参数，k1，k2均大于零；x为系统状态变量。

改进幂次趋近律由幂次项-k1||sαsgn(s)和变速项-k2||x sgn(s)/( ||x+1)组成。当系统状态距离滑模面较远时，幂次项起主要作用，且有：

变速项能够提供足够大的趋近速度。当系统状态距离滑模面较近时，变速项起主要作用，随系统状态变量x自适应调节抖振大小。当系统状态趋近平衡点时，有：

变速项在平衡点附近收敛于±k2x。此时，改进幂次趋近律变换为

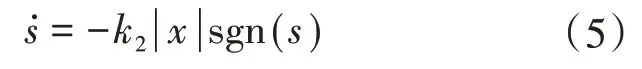
综上，这样设计趋近律既吸收了幂次趋近律快速到达的优点，又采纳了变速趋近律自适应调节滑模抖振的优势，最终使系统状态收敛于平衡点。

2.2 控制性能分析

定义Lyapunov函数：

对式（6）求导，并将式（2）代入，得：

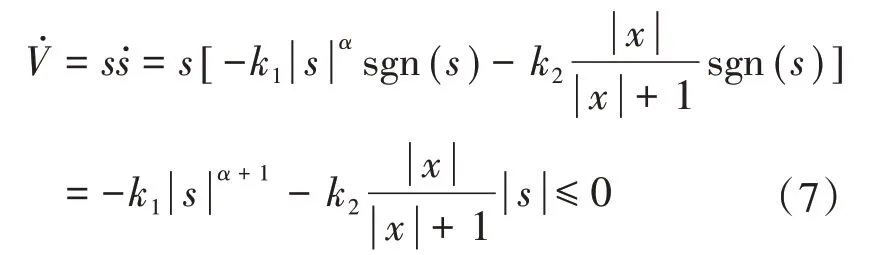
由此可见，改进幂次趋近律满足滑模到达条件。

本文设计的改进幂次趋近律承接幂次趋近律快速到达特性。假设滑模初始状态s(0)＞0，此时改进幂次趋近律：

整理，并求积分，得：

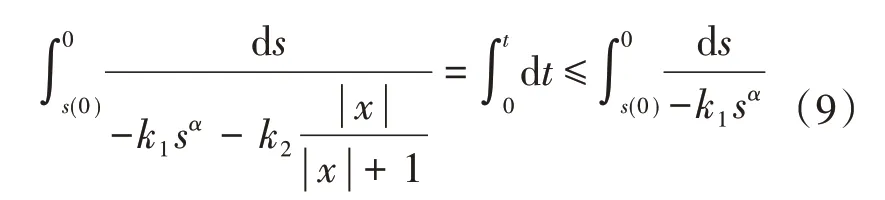
求得：

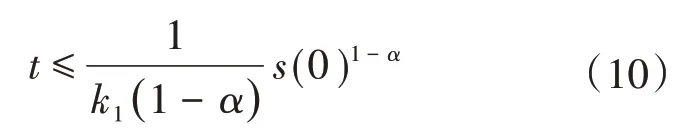
从式（10）可以看出，系统能在有限时间内到达滑模面。

当系统受到有界外部扰动时，此时改进幂次趋近律数学表达式为

式中：d(t)为外部扰动且满足 ||d(t)≤η，η＞0。

对式（6）求导，并将式（11）代入，得：

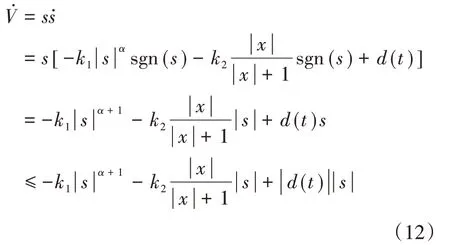
定义k′2=k2|x|/( |x|+1)，整理式（12），得：

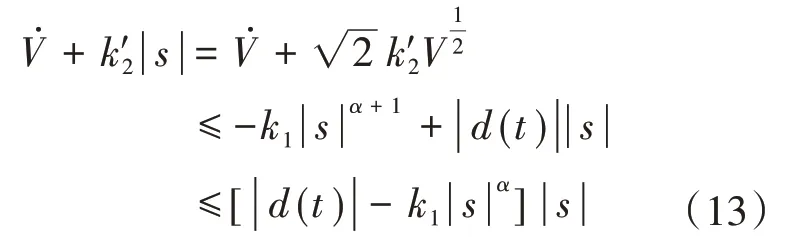
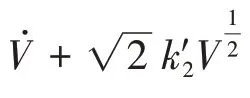
由式（11），求得：

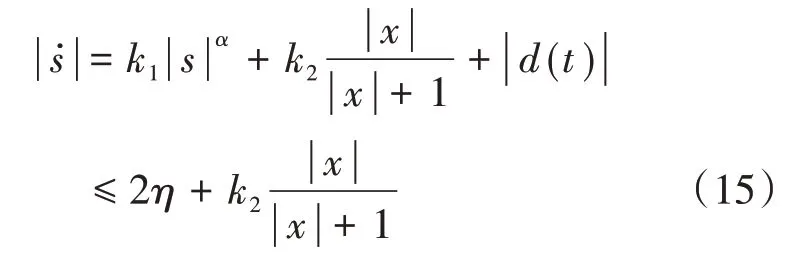
当滑模面收敛到平衡点附近时，变速趋近律趋于零，式（15）变换为

综上，在采用改进幂次趋近律前提下，当系统受到有界外部扰动时，滑模面及其导数能收敛到式（14）、式（16）所示的领域内。

3 基于改进幂次趋近律的三阶滑模控制器设计

3.1 控制器设计

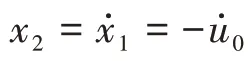
根据式（1），得：

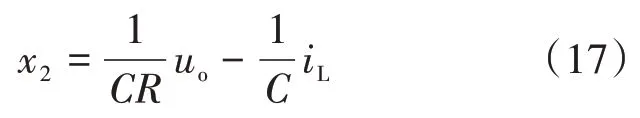
由于电感电流：

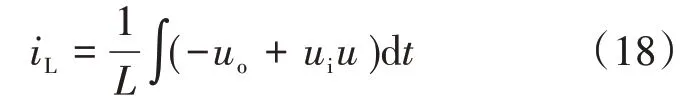
对式（17）求导，并将式（18）代入，求得：

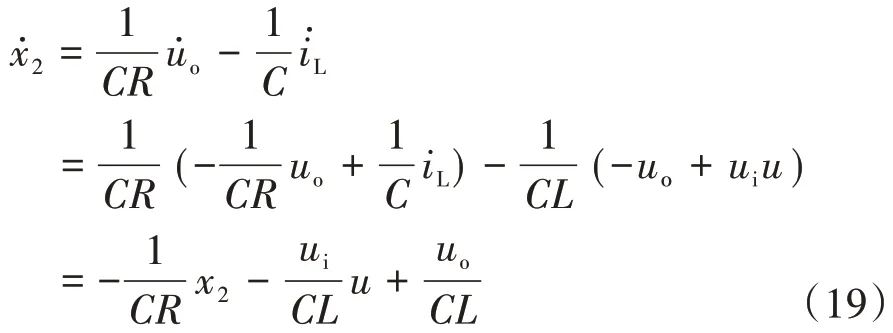
对式（18）求导，可得：

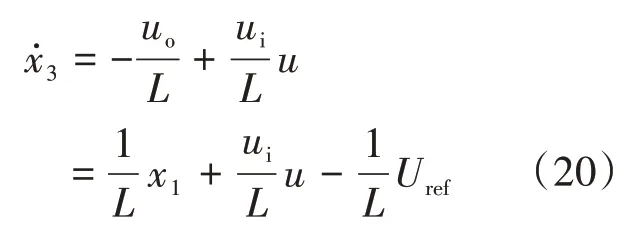
根据式（19）、式（20），求得Buck变换器三阶滑模控制器状态空间方程为

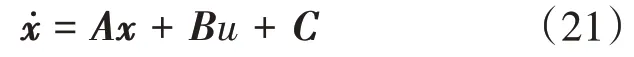
其中 x=[ x1x2x3]T

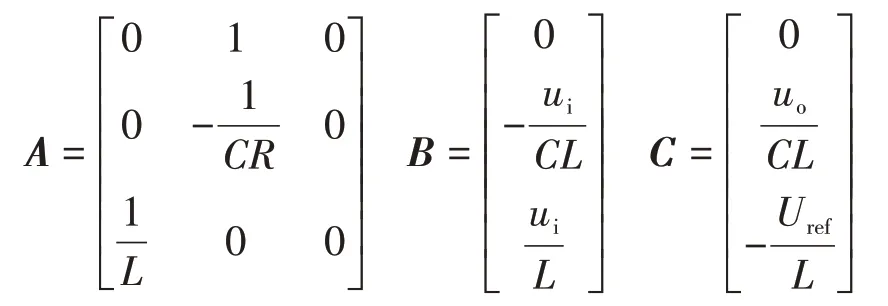
定义线性滑模面

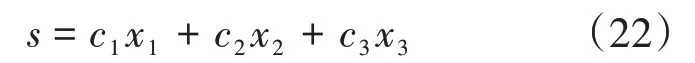
其中，滑模面参数c1，c2，c3均大于零。对式（22）求导，得：

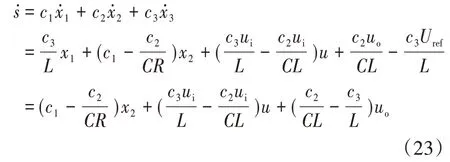
将式（2）代入，求得滑模控制器控制作用u为

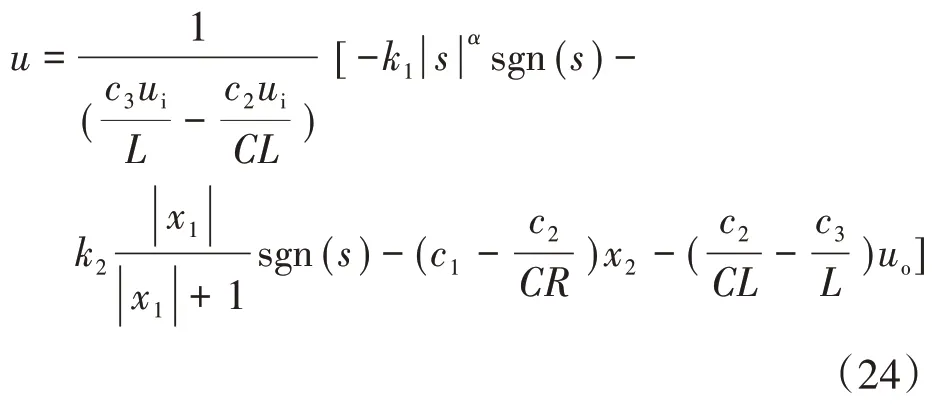
3.2 滑模面参数选择

本文在三阶滑模控制器基础上设计滑模面，滑模面包含电感电流，参数选择具有不确定性，故有必要进一步分析滑模面参数的取值问题。

根据李导数定义，求得：

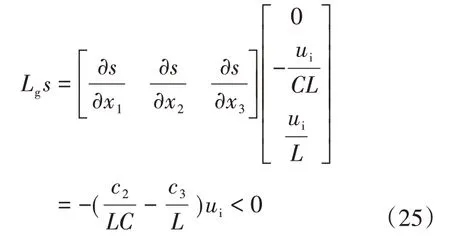
根据式（25），如若满足滑模运动条件，滑模面参数需满足c2＞c3C条件。同样，根据李导数定义，求得等效控制ueq为

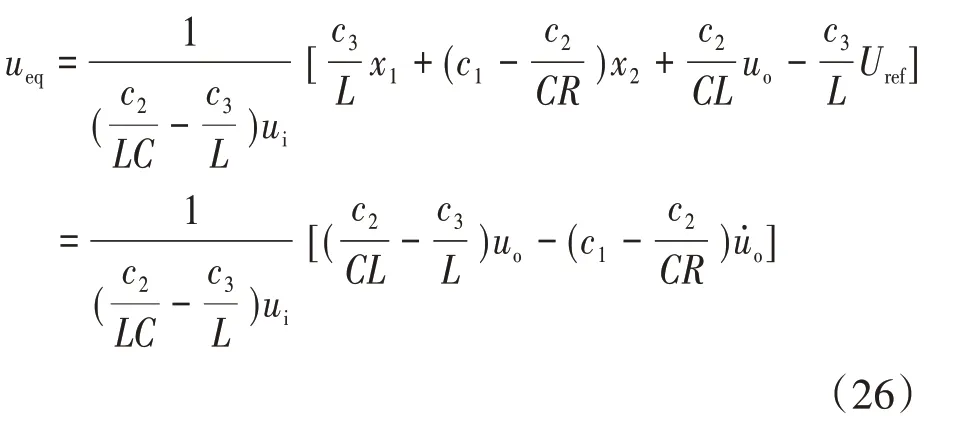
从式（26）可以看出，当滑模面参数满足c2=c1CR条件时，等效控制ueq不受输出电压变化率u˙o影响，此时等效控制ueq=uo/ui。

4 仿真与实验验证

4.1 仿真验证

为验证基于改进幂次趋近律的滑模控制器有效性，通过Matlab/Simulink仿真软件，将改进幂次趋近律与指数趋近律分别应用于Buck变换器进行比较。Buck变换器参数为：ui=20V，L＝10 mH，C＝3.6 mF，R＝10Ω。改进幂次趋近律参数为：k1=20，k2=5，α=1.2。滑模面参数为：c1=30，c2=1，c3=10。图2为基于两种趋近律的Buck变换器输出电压uo比较，图3为基于两种趋近律的Buck变换器电感电流iL比较。

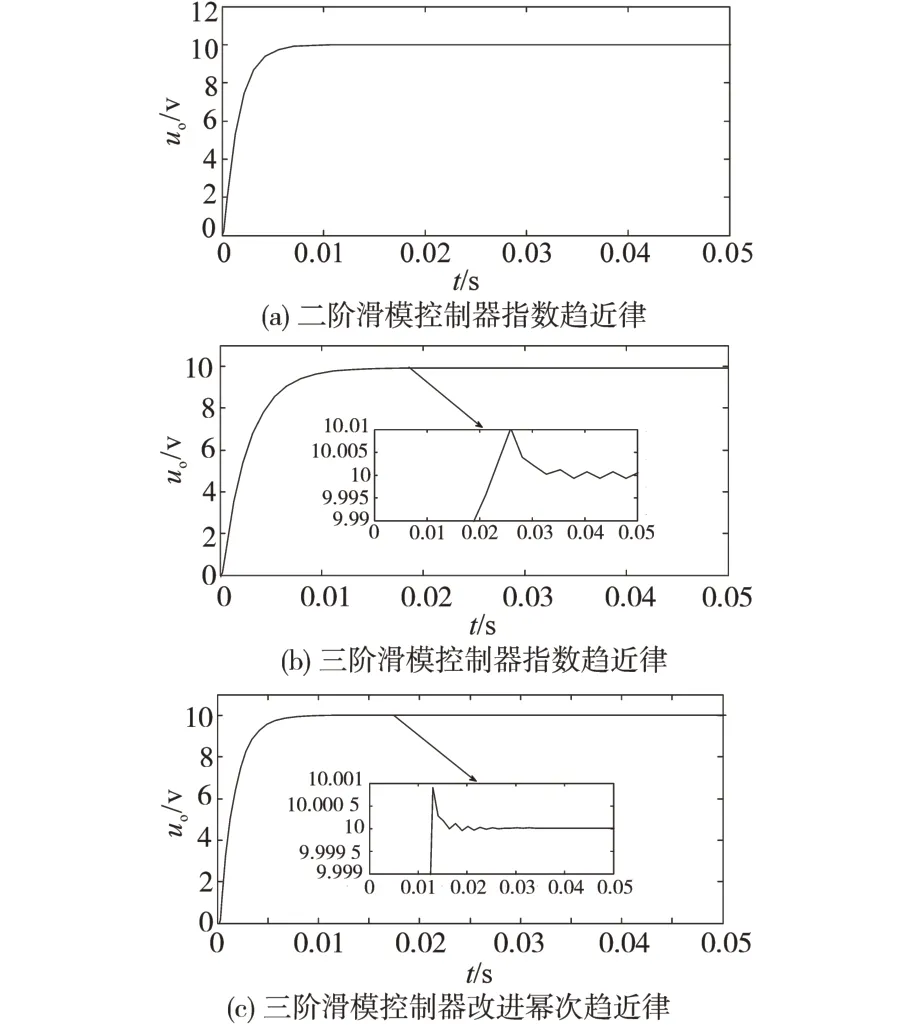
图2 Buck变换器输出电压比较Fig.2 Buck converter output voltage comparison

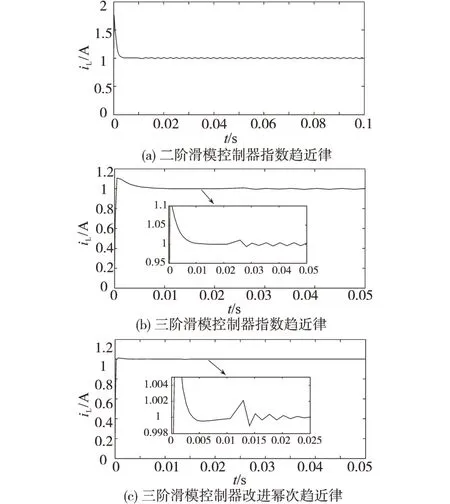
图3 Buck变换器电感电流比较Fig.3 Buck converter inductor current comparison

从图2可以看出，基于指数趋近律的三阶滑模控制器输出电压到达稳态所需时间过长，超调量较大，且到达稳态后不能收敛于平衡点，基于改进幂次趋近律的三阶滑模控制器输出电压到达稳态所需时间较短，超调量相对较小，且到达稳态后随系统状态变化渐近收敛于平衡点。

从图3可以看出，基于指数趋近律的二阶滑模控制器电感电流超调量比三阶滑模控制器大很多。基于指数趋近律的三阶滑模控制器电感电流超调量较大，到达稳态后不能收敛于平衡点。基于改进幂次趋近律的滑模控制器电感电流超调量较小，可随系统状态变化渐近收敛于平衡点。图3进一步表明，通过设计三阶滑模控制器，能够有效控制电感电流，降低电感电流超调量，有利于控制器设计。

4.2 实验验证

为验证基于改进幂次趋近律的滑模控制器有效性，搭建实验平台将其与指数趋近律相比较。Buck变换器参数、改进幂次趋近律参数、滑模面参数与仿真保持一致。其中，Buck变换器输入电压由可编程电源Chroma 62050P提供，开关管采用TI公司的CSD16414Q5，二极管采用STPS20200CT，电感采用TDK公司的VLB12065HT-R36，输出电容采用Murata公司的GRM32ER71H106MA12，负载采用可编程电子负载Agilent 6060B。电流检测采用霍耳电流传感器CHB-25NP。控制板采用DSP28335作为控制芯片。图4为指数趋近律控制方法输出电压实验波形，图5为改进幂次趋近律控制方法输出电压实验波形。其中，图4c和图5c为负载从10Ω突变为5Ω时，输出电压实验波形。

图4 指数趋近律控制方法输出电压实验波形Fig.4 Output voltage experimental waveforms of exponential reaching law control method

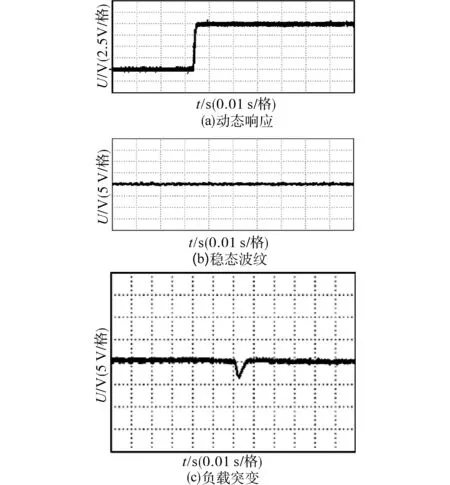
图5 改进幂次趋近律控制方法输出电压实验波形Fig.5 Output voltage experimental waveforms of improved power reaching law control method

从实验波形可以看出，与基于指数趋近律的滑模控制器输出电压相比较，基于改进幂次趋近律的滑模控制器输出电压超调量较小，到达稳态速度快，且到达稳态后电压谐波含量较低。当负载突变时，输出电压超调量较小，回到稳态所需时间更短，抗干扰和带载能力更强，进一步证明本文所提方法的优越性。

5 结论

本文针对Buck变换器三阶滑模控制器，提出一种改进幂次趋近律滑模控制方法。该方法有效提高了系统动态性能，减小了输出电压超调量，降低了系统抖振。通过仿真和实验验证，证实了方法的有效性，对工程实践具有一定借鉴意义。