无PFC LED球泡灯滤波电路对电流谐波的影响研究

闫东辉，谢荣斌，周群，曹庆

（1.四川大学，电气信息学院，四川成都610000；2.贵州电网息烽供电局，贵州息烽551100）

近年来，环保与资源形势日益严峻，采用高效节能灯具是降低能耗的重要举措之一。由于同等光通量下LED功耗远远低于白炽灯，同时具有电光转化效率高（接近60%）、寿命长（可达10万小时）、工作电压低（3 V左右）、易于调光、色彩多样、光束集中稳定、启动无延时等诸多优点，并且政府也在引导LED灯具取代传统的白炽灯，使得LED灯具得到了成规模的应用。但随之而来的是一系列新的问题，其中最突出的便是由LED驱动引发的谐波相关的问题[1-2]。

虽然单个LED产生的谐波对电网的影响很小，但随着LED灯大规模高渗透率应用，大量谐波接入电网，对电网的电能质量扰动不可忽略[3]。IEC61000-3-2标准中对小于25 W的C类照明设备谐波排放标准作出相应规定，如表1所示。目前对LED谐波发射的研究主要分为2类，其一为研究使用PFC技术将电流波形矫正到比较接近正弦的形状，从而抑制电流谐波，降低电流畸变率[4-7]；还有部分学者研究通过PFC技术控制LED的谐波相位，实现局部范围内的谐波抵消从而减少流入电网中的谐波电流[8]。其二，由于成本问题，无PFC的LED照明产品2015年的全球照明市场渗透率达30%，预计2020年将占据全球照明市场的70%。因此研究无PFC技术的LED的谐波发射特性具有重要意义。目前国内外无PFC技术的LED球泡灯谐波发射特性研究主要集中在对不同品牌的灯具进行谐波特性测试，进而对比分析得出电流畸变率（79.89%～198.1%）较高且波动范围较大的结论[9-10]。也有通过建模仿真研究固定区域内的集群无PFC LED照明灯具产生的谐波对分布式电网的影响[11-12]。但是对由于滤波结构及参数不同引起的无PFC LED谐波发射特性的不同，还未有相关方面的研究。

本文通过对无PFC LED球泡灯的π型、倒L型、C型3种常见滤波电路的研究，比较3种滤波电路及参数对3次、5次、7次和9次谐波相位的影响和对谐波电流畸变率的影响，研究不同滤波结构的LED球泡灯组合存在的谐波叠加和消除机理。最后通过不同滤波结构的3个6.5 W的无PFC LED驱动电路实验，验证了理论分析和仿真结果的正确性。

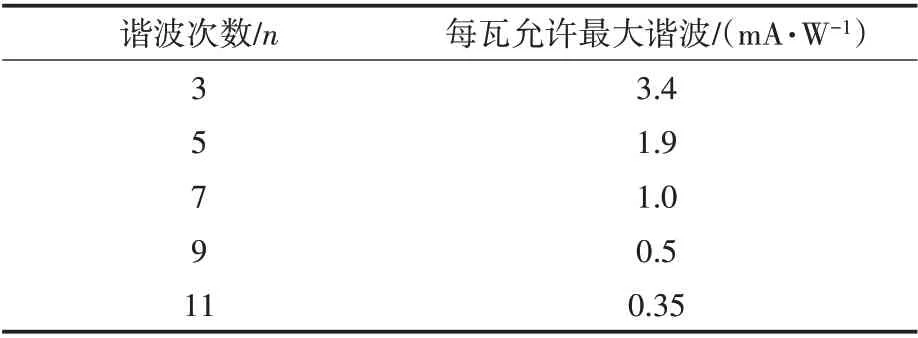
表1 IEC61000-3-2谐波排放标准Tab.1 IEC61000-3-2 harmonic emission standards

1 LED 3种不同滤波电路的电流谐波相位分析

1.1 LED驱动电路模型

家用LED球泡灯驱动电路为典型的恒流降压无PFC驱动电路，图1a为驱动电路模型。该模型由220 V交流电源、单相桥式整流电路D、滤波电路F、降压电路B、负载RL构成。其中加入滤波电路F滤除整流后的部分残留交流成份，可以有效保证负载正常工作。在LED驱动电路拓扑中最常见的3种滤波结构（π型、倒L型、C型）如图1b所示。

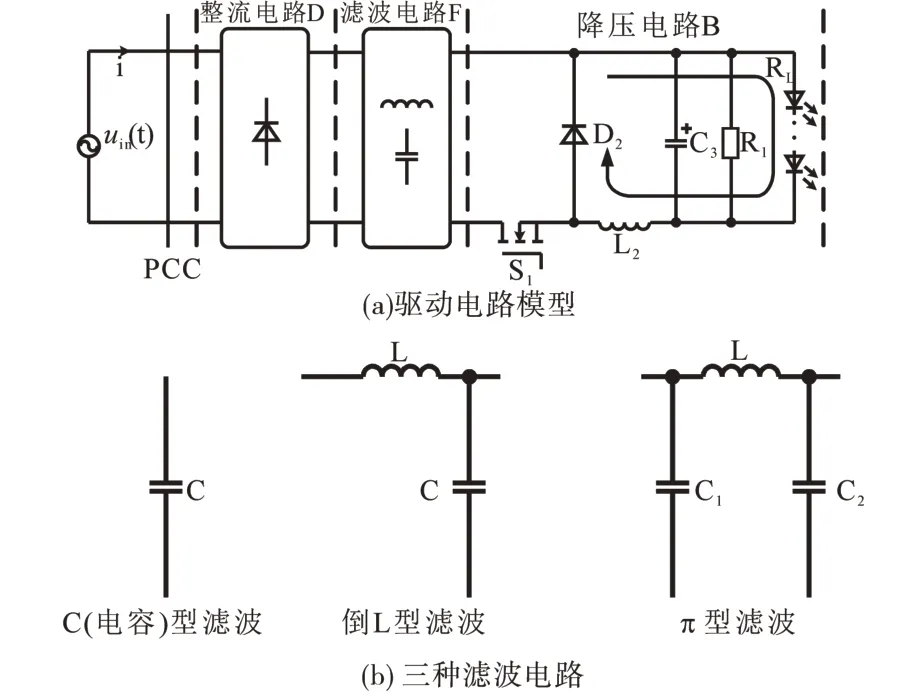
图1 LED球泡灯驱动电路与滤波电路Fig.1 Drive circuit and filter circuit of LED bulb lamp

1.2 C型滤波电路

C型滤波结构作为一阶滤波电路，具有结构简单、体积小等优点，但是也存在需要电容量太大，基波损耗大等问题[13]。因此使用此种滤波结构的LED驱动电路会使得PCC（公共连接点）处的谐波呈现其独有的特性，假设电压无畸变情况下，其电流表达式如下式所示：

式中：ω为角频率；h为谐波次数；θh为各次谐波初相角（计时零点到正弦量零点之间的角度）；aih为傅里叶级数的偶函数；bih为傅里叶级数的奇函数；Ih为各次谐波电流有效值。

滤波电容值C与各次谐波初相角之间的关系趋势图，如图2所示。

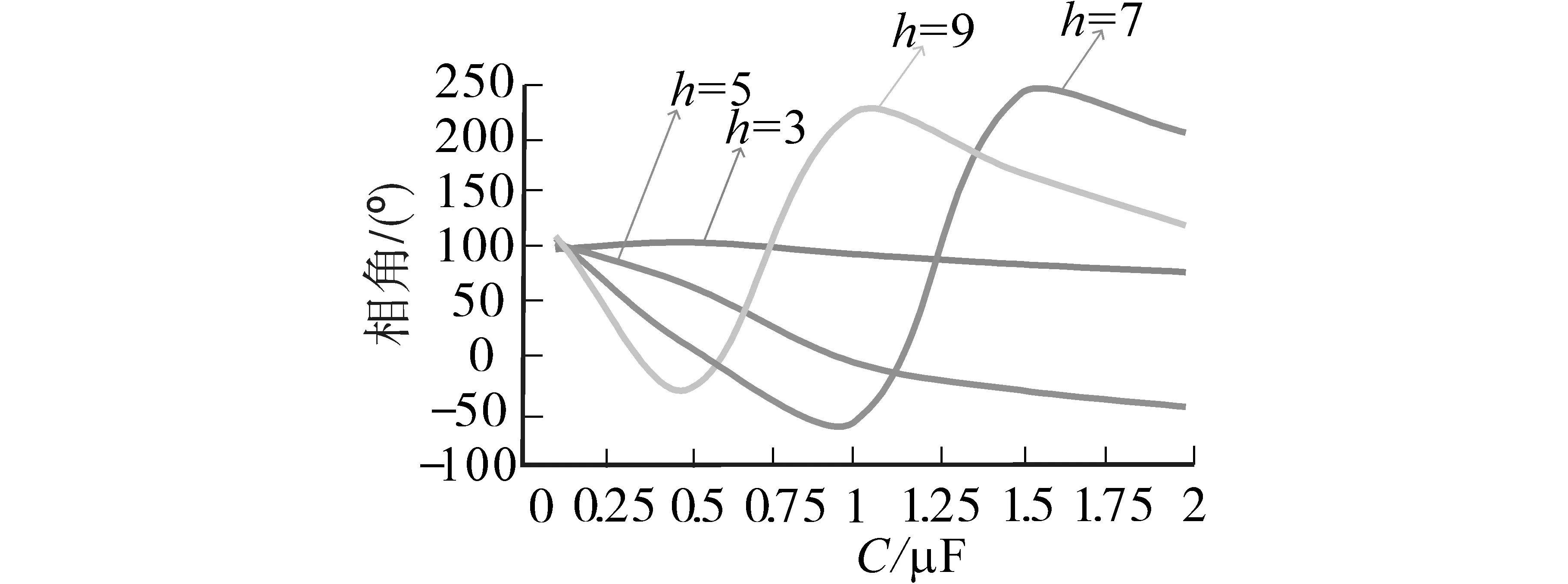
图2 滤波电容值C与各次谐波初相角之间的关系图（C型）Fig.2 Relationship between the filter capacitance value C and initial phase angle of each harmonic（C-type）

图2中，当电容值取值范围为0μF＜C≤2μF时，负载端的纹波在（110±10）V之间，可以使LED灯正常工作，为使3种结构可以在同一标准下有对比性，将倒L型和π型滤波结构电容取值范围固定在0μF＜C≤2μF。

1.3 倒L型滤波电路

电容电感倒L型二阶滤波电路包括1个电容器和1个电感器，相比于一阶滤波电路和三阶滤波电路，二阶滤波电路的滤波性能最好，但是与三阶滤波电路相比，其基波损耗较高[13]。使用倒L型滤波电路的LED在PCC处电流表达式如下式所示：

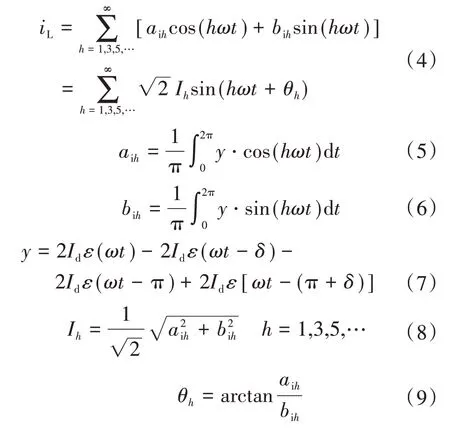
式中：Id为流经二极管的电流；ε为阶跃函数。

滤波电容C和滤波电感L与各次谐波初相角之间的关系如图3和图4所示。

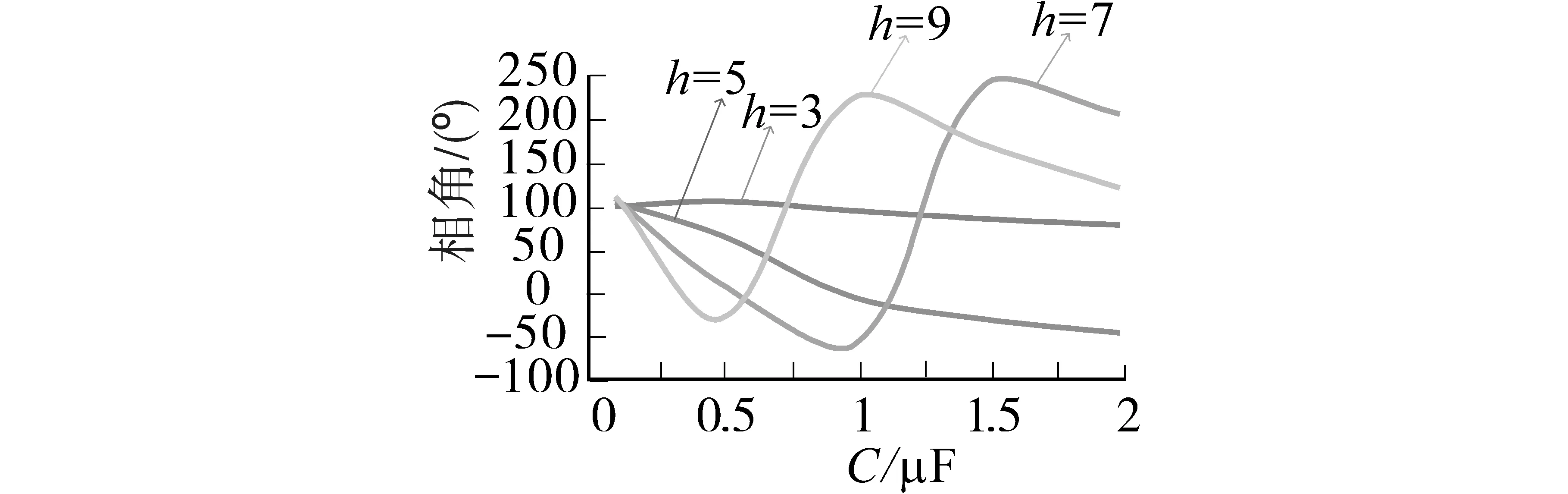
图3 滤波电容值C与各次谐波初相角之间的关系图（倒L型）Fig.3 Relationship between the filter capacitance value C and the initial phase angle of each harmonic（inverted-L-type）

图4 滤波电感值L与各次谐波初相角之间的关系图（倒L型）Fig.4 Relationship between the filter inductor value L and the initial phase angle of each harmonic（inverted-L-type）

图4中，当滤波电感取值在180～400μH范围时，负载端的纹波在110±10 V范围，可以保证LED正常发光，无频闪现象。为使3种结构可以在同一标准下有对比性，将倒L型和π型滤波结构的电感取值范围固定在180～400μH。

1.4 π型滤波电路

电容电感π型滤波电路（LCπ型）包括2个电容器和1个电感器，在整流电路之后滤除电流中的交流成分。π型滤波结构作为一个三阶滤波器，相比于一阶和二阶滤波器，其基波损耗大大减少[13]。使用此种滤波器的LED在PCC处的电流表达式如下式所示：

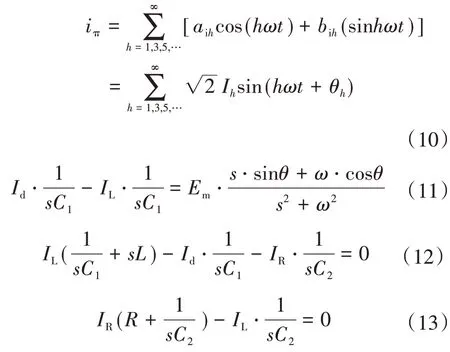
联立式（11）～式（13）即可解出Id。

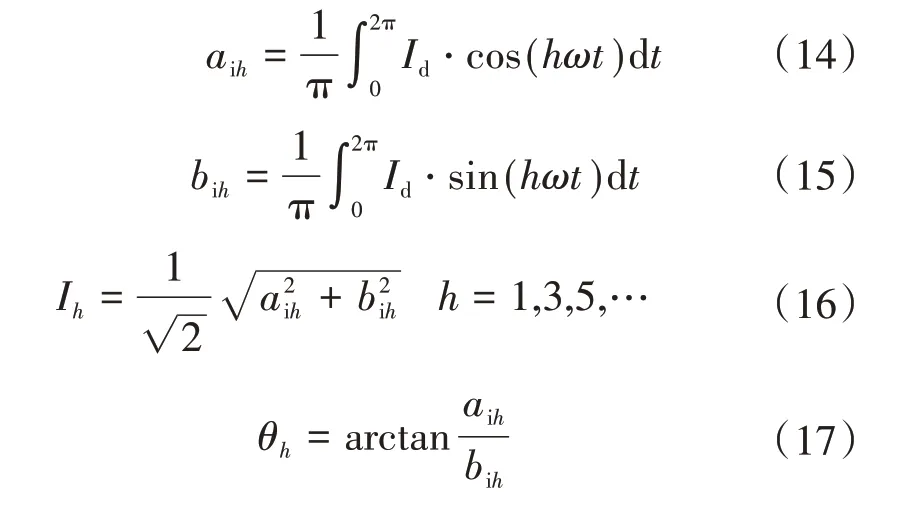
式中：Em为电压值；IL为流经滤波电感的电流；IR为流经负载的电流；C1，C2为滤波电容值；R为负载值；s为复变量。

滤波电容C、滤波电感L与各次谐波初相角之间的关系如图5和图6所示。

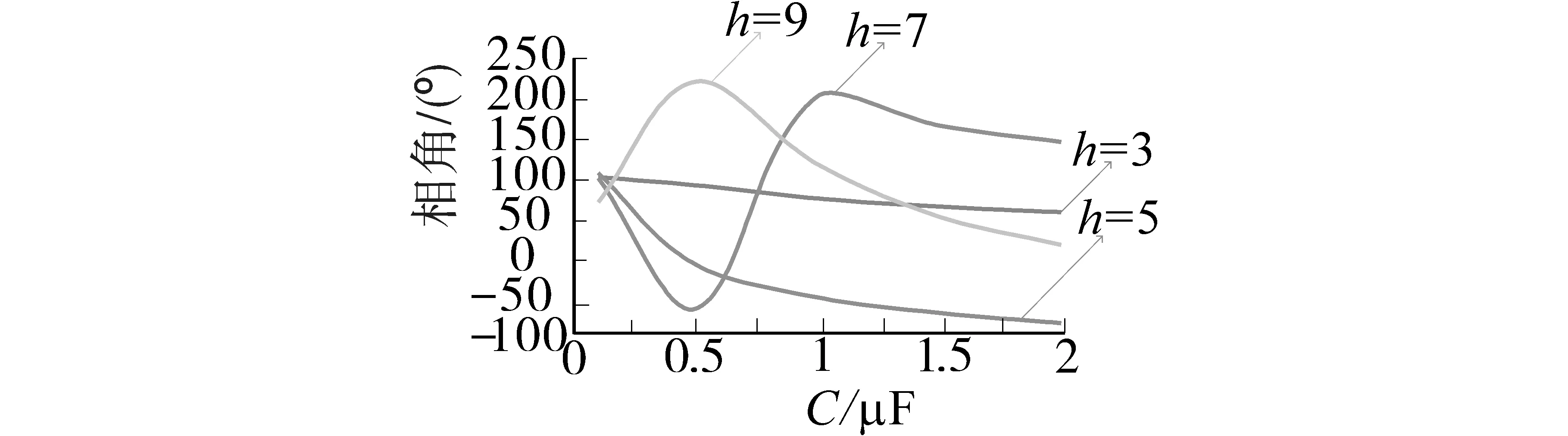
图5 滤波电容值C与各次谐波初相角之间的关系图（π型）Fig.5 Relationship between the filter capacitance value C and the initial phase angle of each harmonic（π-type）

图6 滤波电感值L与各次谐波初相角之间的关系图（π型）Fig.6 Relationship between the filter inductor value L and the initial phase angle of each harmonic（π-type）

1.5 3 种滤波结构LED的电流谐波发射特性对比分析

由于单盏无PFC的LED球泡灯电流引起的总谐波失真（total harmonic distortion，THD）要远远大于电压引起的，因此主要分析PCC处的电流情况，3种滤波电路的电流仿真波形、PCC处谐波发射特性如图7和表2所示。图7中，Uin波形为示意图，未标注纵坐标数值。

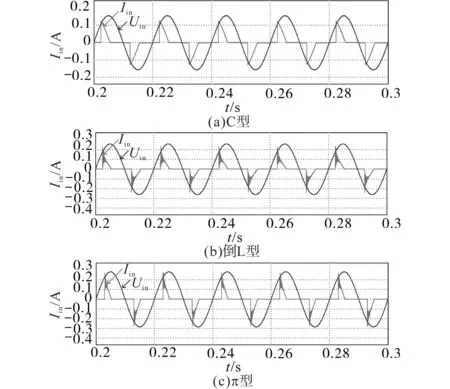
图7 C型、倒L型、π型滤波结构的PCC处波形Fig.7 Waveforms of C-type，inverted-L-type，andπ-type filter structures at PCC

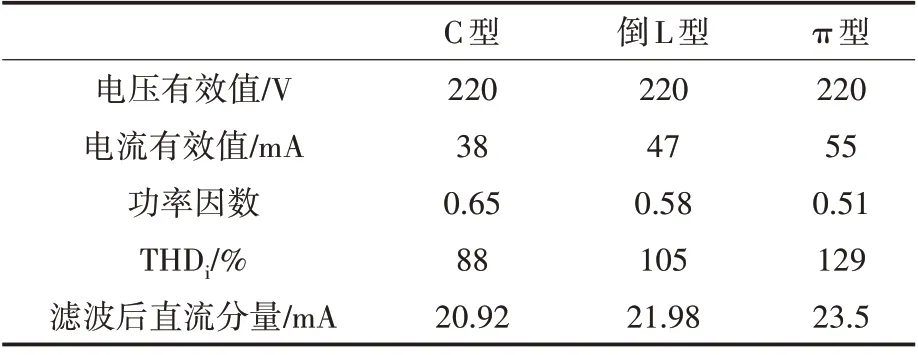
表2 不同结构的驱动电路PCC处谐波发射特性Tab.2 Harmonic emission characteristics of the drive circuit with different structures

由表2可以看出，无PFC的LED驱动电路中使用不同的滤波结构时，3种滤波结构在PCC处的电压有效值相同，均为220 V，而电流有效值不同，C型滤波结构的电流有效值最小，π型滤波结构的电流有效值最大。但是从功率因数来看，C型滤波结构的功率因数（0.65）要高于倒L型（0.58）和π型（0.51）。3种滤波结构在PCC处产生的电流畸变率不同，其中C型滤波结构产生的电流畸变率最低，为88%，π型滤波结构产生的畸变率最高，为129%。由于3种滤波结构的主要作用都是滤除经过整流电路之后残留的交流电流分量，同时保证后面的恒流型降压电路正常工作，因此文章也研究了在无PFC的LED中3种滤波电路作用之后的直流分量，其中π型滤波电路（23.5 mA）要高于倒L型滤波电路（21.98 mA）和C型滤波电路（20.92 mA）。图7所示的3种不同滤波结构的无PFC LED球泡灯在PCC点处的电流波形图，经过FFT分解后如图8所示，只含有3次、5次、7次、9次等奇次谐波，其含量均已超过10%。而在低压电力配电网系统中3次、5次、7次、9次谐波是最为常见的奇次谐波且含量较高，与IEC61000-3-2中对C类设备（照明用具）的谐波排放标准对比如表3所示。

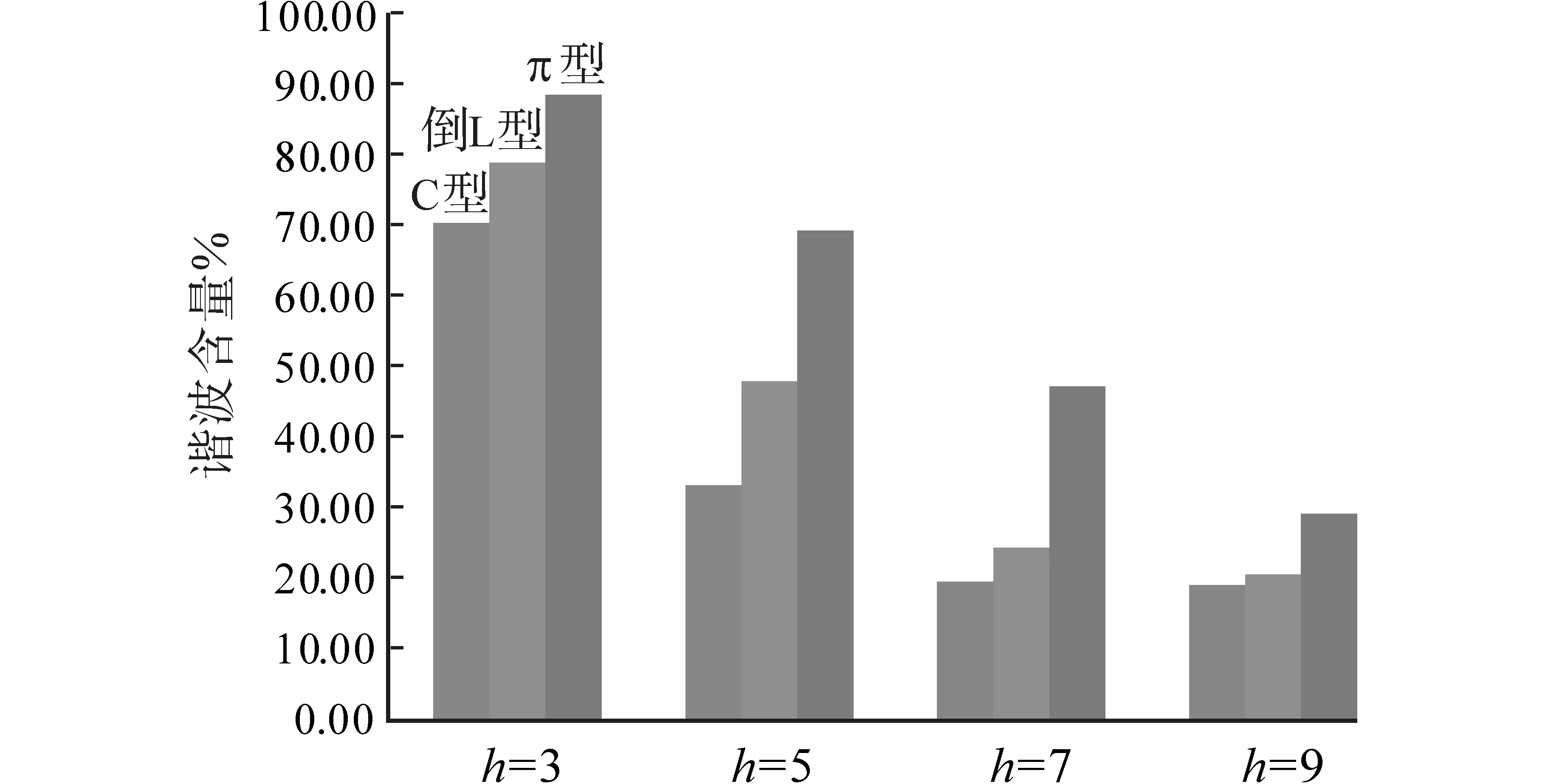
图8 3种滤波结构下的各次谐波含量图Fig.8 The harmonic content of each harmonic for the three filter structures

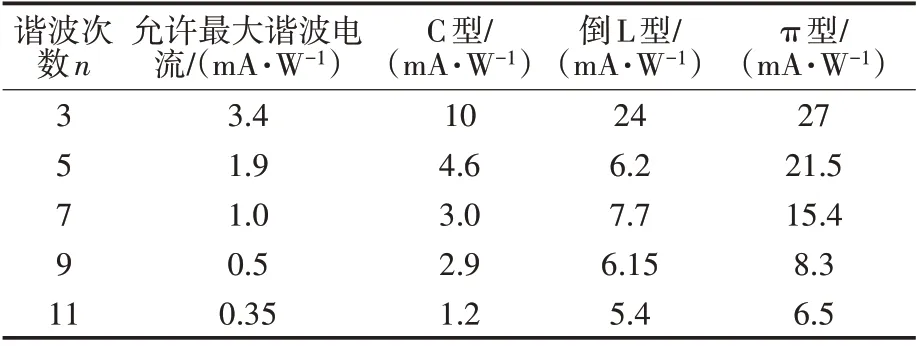
表3 三种不同滤波结构的谐波电流Tab.3 Harmonic currents of three different filter structures

由表3可以看出，各次谐波含量均超过标准，在3种不同滤波结构中3次谐波含量最大，9次谐波含量最小，且随着谐波次数的升高，其含量依次递减。由于π型滤波结构的无PFC LED驱动电路在PCC处电流畸变率最高，因此其3次、5次、7次、9次谐波含量均高于C型和倒L型。将3种不同滤波结构的各次谐波的初相角随着电容变化关系进行对比，如图9所示。

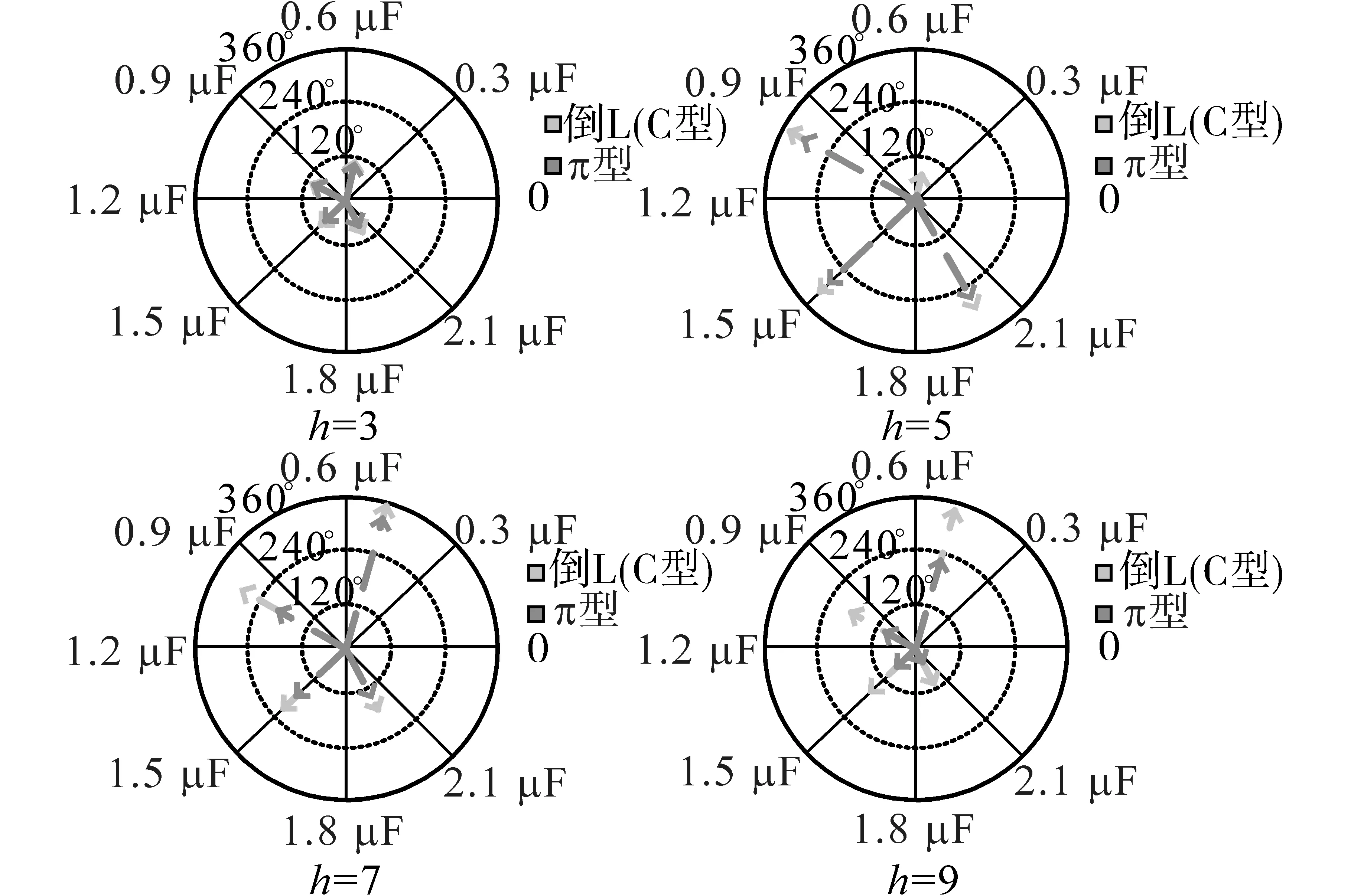
图9 谐波初相角对比图Fig.The diagram of harmonic initial phase angle comparison

通过图9可以看出，3种滤波结构在PCC处的3次、5次、7次、9次电流谐波初相角有一定的规律。C型滤波结构和倒L型滤波结构的3次、5次、7次、9次谐波初相角完全一致，这与图4和图6中初相角不随电感值变化的规律相吻合，因此说明3次、5次、7次、9次谐波的初相角不会受到电感值的影响。比较3种结构的各次谐波初相角可以看到，3次谐波的差异最小，在6°～17°之间，9次谐波的差异最大，在37°～251.4°之间。并且随着谐波频率从3次增高到9次，差异也随之从相差6°增大到相差251.4°。随着电容值的变化，C型和倒L型滤波结构的电流谐波初相角变化（-20°～120.5°）相比于π型滤波结构的电流谐波初相角变化（20°～223°）要小一些。

2 不同滤波结构LED并联后的电流谐波分析

为了分析相同功率下不同滤波结构的LED球泡灯组合后的谐波发射特性，将不同滤波结构的LED球泡灯并联于一个供电系统中如图10所示。

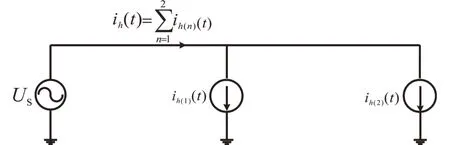
图10 不同滤波结构的LED球泡灯并联图Fig.10 Parallel diagram of LED bulbs with different filtering structures

分析图10所示电路在PCC点处的电流特性，如下式所示：

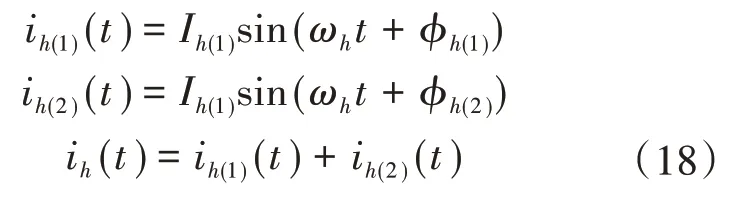
其中 ωh=2πhf

式中：1，2分别代表2种不同的滤波结构；I为电流有效值；i为电流瞬时值；ωh为角频率；φh为各次谐波初相角。

任取2种不同滤波结构的LED球泡灯作分析如下：

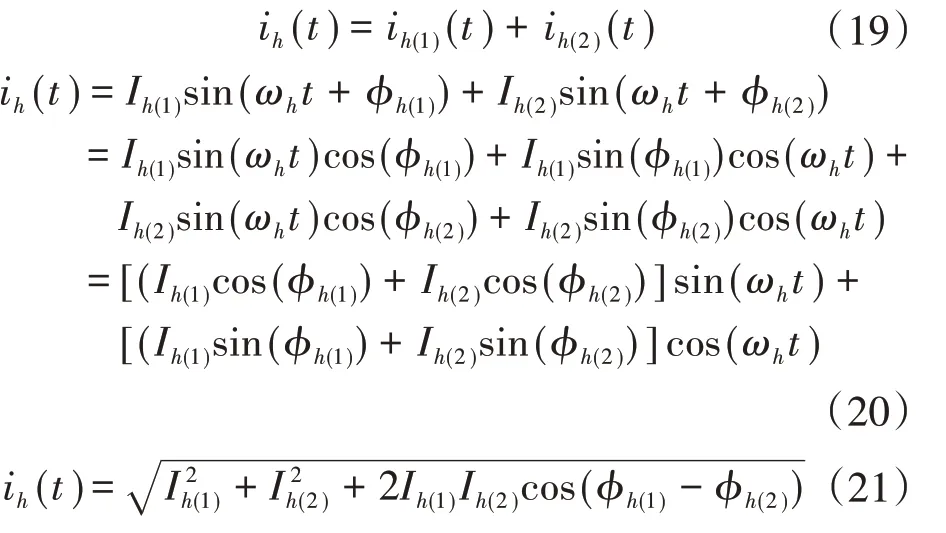
当φh（1），φh（2）∈[0，π]，若φh(2)-φh(1)＜90°，则

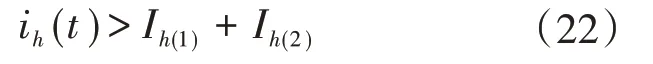
若φh(2)-φh(1)＞90°，则

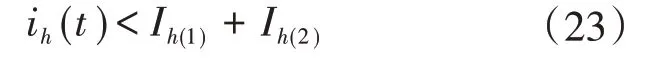
由式（22）和式（23）可以看出，只要任意2种滤波结构的LED球泡灯各次谐波初相角之间夹角小于90°，则该次谐波电流总量增加；夹角大于90°则减小。在C取1.5μF时将不同滤波结构的LED驱动电路两两并联组合仿真，结果如表4所示。

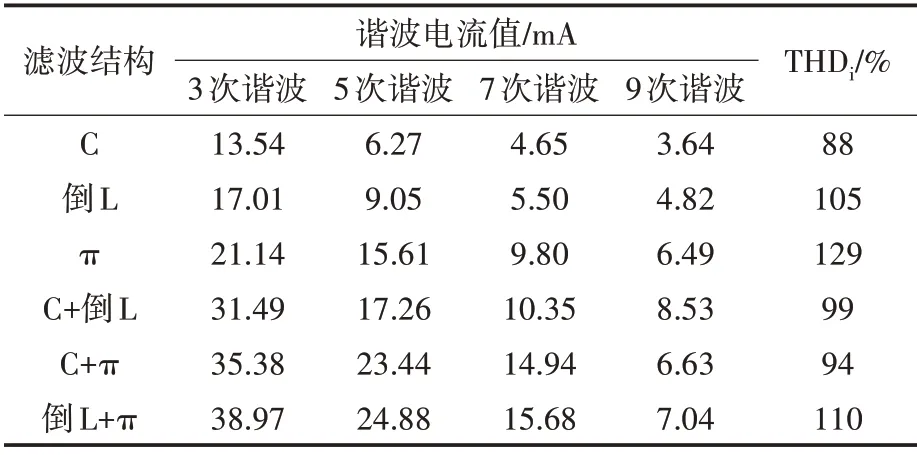
表4 不同滤波结构的LED并联后谐波分析Tab.4 Harmonic analysis of LED parallel connection with different filter structures

由图9和表4中可以看出，C型和π型的3次、5次、7次谐波初相角之间的夹角小于90°，所以组合之后PCC处3次、5次、7次谐波电流含量理论上应该为二者之和，但是考虑到并联的2个LED灯之间会有相互影响，因此组合之后的谐波电流值会略微大于二者之和，这也就验证了各次谐波初相角之间的夹角小于90°时会出现谐波叠加。C型和π型的9次谐波初相角之间的夹角大于90°，所以组合后PCC处的9次谐波电流含量小于二者之和，这也就验证了各次谐波初相角之间的夹角大于90°时会出现谐波抵消。C型和倒L型的3次、5次、7次、9次谐波的相角完全一致，因此组合之后谐波电流含量理论上应该等于二者之和，但是考虑到2盏LED的相互影响，因此组合之后的结果近似等于二者之和。虽然两两组合后3次、5次、7次谐波电流含量会增加，但是总的电流有效值也会增加，所以组合后总的电流畸变率THDi处于二者之间。根据上述结论，结合图2、图3和图5中的谐波各次初相角随电容值的变化趋势，选取使各次谐波初相角之间的夹角大于90°的2个电容值，电感值取相同值（初相角不随电感值变化），将所选的滤波参数用于2盏并联的不同滤波结构LED球泡灯的滤波电路中，以此达到一定程度上抑制网侧谐波电流的目的。

3 实验结果及分析

为了验证上文的理论分析和仿真结果，在实验室环境下用3个不同滤波结构的无PFC LED驱动电路进行了实验验证，结果如下所示。

在实验室环境中对同一主拓扑电路采用3种不同的滤波结构，在电容值C为1μF，1.5μF，2μF时测试各次谐波初相位分布，如图11所示，其与理论结果和仿真结果均有良好的吻合性。

图11 C型、倒L型、π型初相位实验图Fig.11 Initial phase experimental diagram of C-type，inverted L-shaped，π-type

测试PCC处的电流波形和谐波发射特性如图12和表5所示，可以看出电流畸变较为严重，和仿真时结果基本吻合，其中C型为89%，倒L型为109%，π型为130%。由于随着滤波阶数的提升，基波损耗逐渐降低[13]，并且不同的滤波结构驱动电路中PCC处的各次谐波含量也不相同，因此相同负载下使用3种滤波结构的LED球泡灯网侧的电流波形峰值存在较大差异。3种滤波结构的电压有效值均为220 V，电流有效值分别为：C型40 mA，倒L型48 mA，π型53 mA。

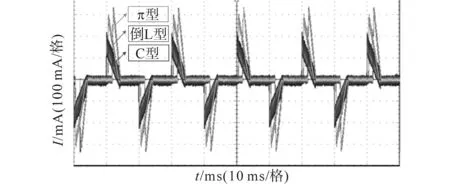
图12 C型、倒L型、π型的实验波形Fig.12 Experimental waveforms of C-type，inverted-L-type andπ-type

表5 谐波发射特性测试结果Tab.5 Test results of harmonic emission characteristics

当C值取1.5μF时，将3种不同滤波结构的LED球泡灯两两组合测试结果如表6所示，和仿真结果基本一致。当滤波电容C值在0.1～2μF变化时，LED驱动电路可以正常工作，低于0.1μF或者超过2μF时，LED球泡灯会出现闪烁和变暗的现象，因此在上文中研究电容变化引起电流谐波初相角变化时，考虑将电容值的范围控制在0.1～2μF。

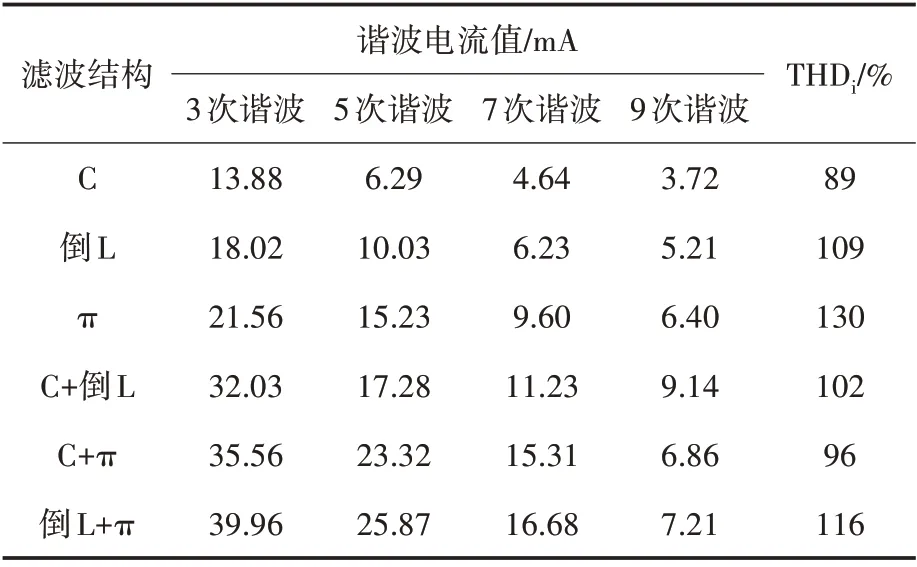
表6 不同滤波结构的LED并联后谐波分析实验数据Tab.6 Experimental data of harmonic analysis of LEDs connected in parallel with different filtering structures

4 结论

本文基于无PFC LED驱动电路模型，从滤波结构、滤波参数和谐波电流初相角方面通过理论研究和实验验证的方法对无PFC LED球泡灯的谐波发射特性进行了研究。当使用不同的滤波结构时，其PCC处的THDi不相同，其中C型滤波结构的最低，π型的最高。3次、5次、7次、9次谐波的初相角只与滤波电路中的电容值C有关并且随其变化而变化。当2种不同滤波结构的LED并联组合，各次谐波初相角之差小于90°时，总谐波电流会增加，大于90°时总谐波电流会减小。因此这就为进一步实现局部环境下不同种滤波结构的无PFC LED驱动电路之间谐波的自抵消研究和集群LED谐波发射特性的研究提供了理论支撑。