不平衡电网下储能系统直流纹波分析及抑制策略

余万荣，丁宇洁，李欢，肖小兵，田浩，蒋泽甫

（1.贵州电网有限责任公司安顺供电局，贵州安顺561000；2.清华大学电力系统及发电设备控制和仿真国家重点实验室，北京100084；3.清华大学电机系北京100084；4.贵州电网有限责任公司电网规划研究中心，贵州 贵阳550003）

近年来，随着资源、环境问题日益严峻以及人们环保意识的增强，基于电力电子变流技术的光伏（photovoltaic，PV）、风电（wind generation，WG）等可再生能源（renewable energy sources，RES）得到了迅速发展，其装机总容量不断上升[1-2]。同时，由上述单元构成的微电网逐渐得到推广、应用。为降低可再生能源发电间歇性、不确定性等对微电网稳定性造成的不利影响[3-4]，通常在微电网中配备一定容量的储能装置。根据不同应用环境和应用等级，目前工程中储能主要为采用两电平变流技术的电池储能系统，但基于多电平技术的储能系统正逐渐受到广泛关注和研究[5-7]。

由于微电网容量等级相对较小，因此单相负载或不平衡负载很容易引起微电网的不平衡运行。电网的不平衡严重影响到了微网中变流器的安全可靠运行以及电能质量等[8]。此外，不平衡的负载将在变流器直流母线电流中引入低频纹波分量[9]，而文献[10]指出低频纹波电流将会增大燃料电池的瞬时输出功率，这将使燃料电池容量增大，成本增加。且当二次纹波电流超过额定电流的8%时，电池效率下降，使用寿命缩短。

针对上述问题，文献[9]通过控制方法利用LCL滤波器中的电容提供不平衡负载引入的二次脉动功率，但该方法需要较大通流能力的滤波电容。文献[11]采用两级拓扑方式，通过控制前级变换器抑制低频脉动分量进入电池侧，但该方法不能完全消除进入电池的低频电流，且流经前级变流器的功率较大，系统效率降低。

根据电力系统中“电力弹簧”的概念[12]，本文在此基础上提出了直流母线并联Buck-Boost型直流电力弹簧（DC electrical spring，DCES）的有源低频电流纹波抑制方法。首先，通过建立三相两电平变流器的开关函数模型，分析了不平衡负荷下，直流母线低频纹波电流的产生机理，并给出了电流的时域表达式。随后，建立了DCES的频域模型，给出了采用改进型复合控制的低频纹波电流抑制方法，并利用小增益理论对该控制策略的稳定性进行了分析。最后，利用仿真模型和实验样机对DCES以及所提控制策略的可行性进行了验证。

1 低频纹波电流分析

为简化不平衡负荷条件下直流侧低频纹波电流产生机理的分析，本文以如图1所示的三相两电平储能逆变器为例进行讨论，且逆变器采用正弦脉冲宽度调制（sinusoidal pulse width modulation，SPWM）。同时假设图1中交流测三相电流ia，ib，ic均为工频正弦波。id表示直流母线电流；Q1～Q6分别表示三相桥臂中的功率器件。

图1 三相储能逆变器并网结构图Fig.1 Structure of grid-tied three-phase inverter

假设Sa，Sb，Sc分别为对应各相的桥臂的开关函数，且规定桥臂上与正母线相连的功率器件导通时Sj=1，j=a，b，c；与负母线相连的功率器件导通时Sj=-1。

采用开关函数的傅立叶形式构成SPWM调制逆变器的开关门信号，用以描述逆变器的电流和电压，并通过分析得出逆变器直流侧输入电流的谐波分量。电压型逆变器开关函数的傅里叶表达式为

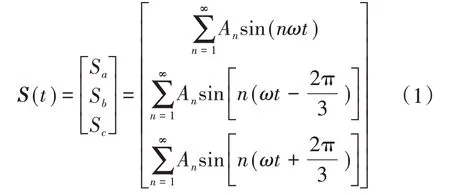
式中：ω为逆变器输出电压的基波角频率；An为输出电压n次谐波的幅值系数，n=1，3，5，7，…。

开关函数描述的逆变器直流侧电流的表达式为

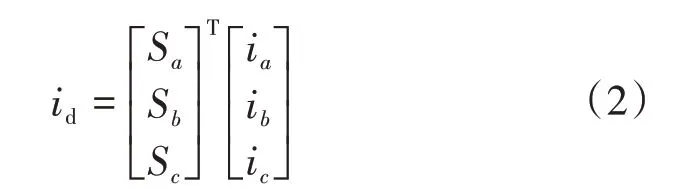
整理得

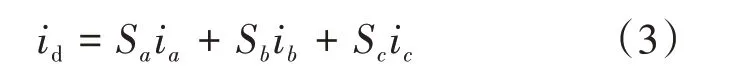
当图1所示逆变器接入的电网存在三相不平衡负荷时，不考虑开关器件死区时间的影响，此时三相电流表达式为

式中：φ为输出电流相位角；Ia，Ib，Ic分别为各相电流的幅值。

对于图1所示三相三线制逆变器，电流零序分量为0，即

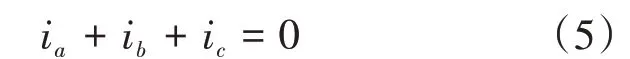
利用对称分量法对式（4）进行处理，可得不平衡相电流中正、负序分析分别为

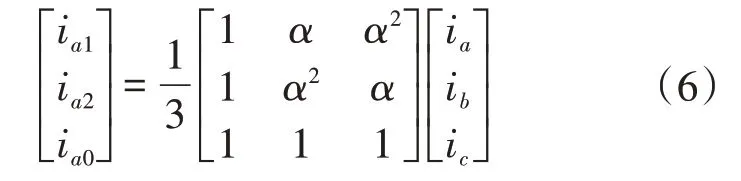
其中 α=ej120°

式中：ia1，ia2，ia0分别为正序、负序和零序电流分量。

将式（4）和式（5）代入式（6），整理得电流各序分量表达式分别为

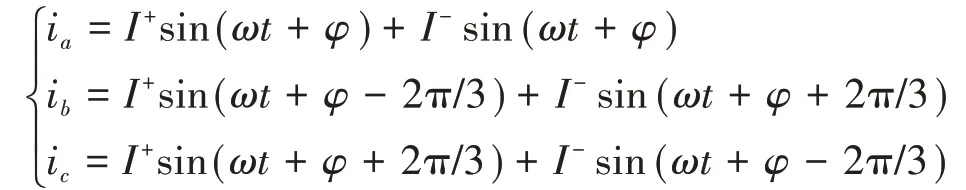
其中

式中：I+为逆变器输出电流的正序分量幅值；I-为负序电流分量幅值；γ为输出三相电流的不平衡度。

结合式（1）、式（3）和式（7），可得不平衡负荷情况下逆变器直流侧电流时域表达式如下式：

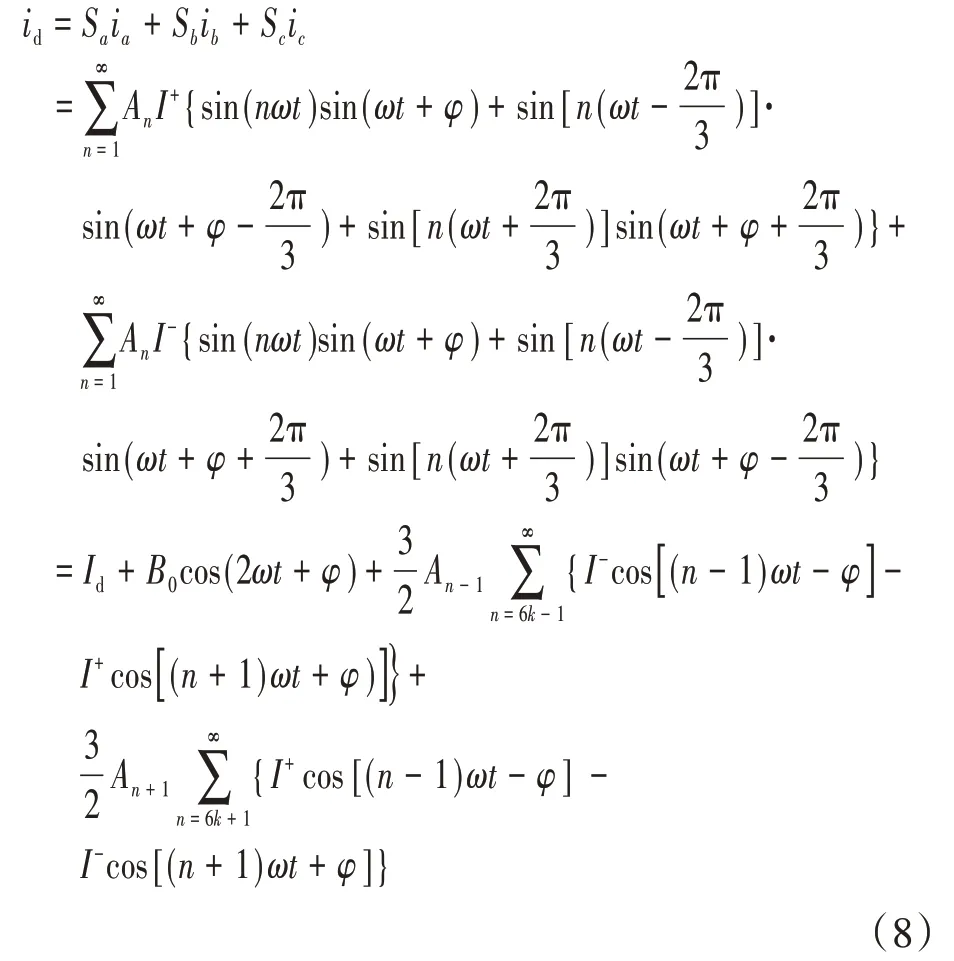
其中

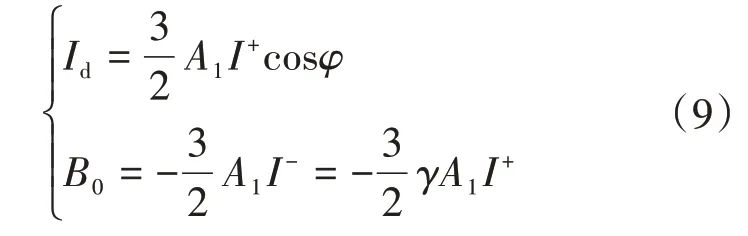
根据式（8）和式（9），可以看出，在忽略功率器件死区时间情况下，带不平衡负荷运行时，三相逆变器的直流侧电流主要包含直流分量、二次纹波分量以及其他高次谐波。其中二次电流纹波由三相不平衡负荷产生的负序电流引入，且其幅值与三相负荷的不平衡度γ成正比，即微网中负荷的不平衡度愈严重，逆变器直流母线上的二次电流纹波越大。文献[10]指出，过大的低频电流脉动将加剧储能系统电池的热老化，降低使用寿命。

此外，由于占主要成分的电流分量频率较低，传统的通过直流母线支撑电容吸收电流纹波的方法难以达到满意效果，且大容量的电容将进一步提高系统成本并增加体积。针对上述问题，本文提出采用基于Buck-Boost拓扑结构的DCES对低频电流分量进行有源抑制。

2 Buck-Boost型DCES及控制策略

图2给出了集成DCES后的储能变流器拓扑结构。其中，电感L、电容C以及功率器件Q7和Q8组成DCES。相比于图1中直接在直流侧并联电容的方法，本文所提有源抑制方法能更为有效地吸收电流低频纹波分量。

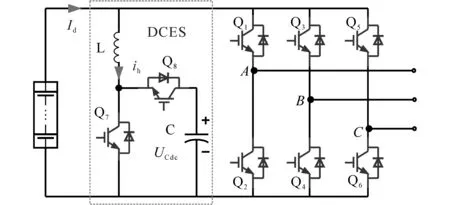
图2 集成DCES的逆变器拓扑Fig.2 Topology of inverter integrated with DCES

2.1 DCES频域模型

根据图2可以看出，DCES的拓扑结构为Buck-Boost型，分析其工作原理可知，在1个二倍工频周期内，其先后工作与Boost模式和Buck模式。为建立DCES的频域模型，根据上述工作模式，分别进行讨论。当DCES工作在Buck模式时，其拓扑结构等效为图3所示。其中，电阻R为电容C的等效并联电阻。

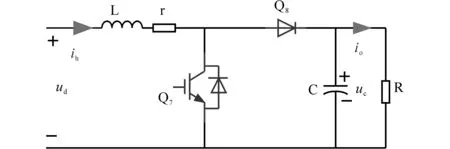
图3 Boost工作模式下等效电路结构Fig.3 Equivalent topology of DCES under Boost mode

根据图3，可得电容电压uc和电感电流ih的时域模型表达式为

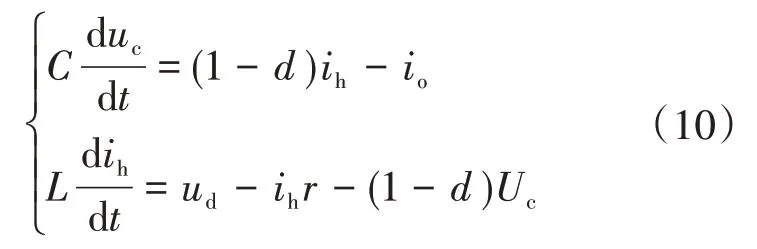
式中：ud为直流母线电压；Uc为电容稳态电压；r为电感寄生电阻；d为某一时刻时的工作占空比。

对电压、电流添加小扰动后可得

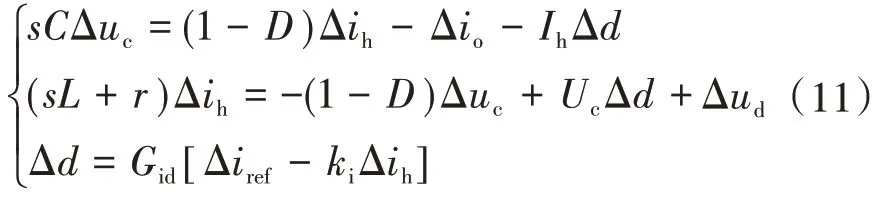
式中：ki为电流采样增益；Gid为控制系统的指令增益，本文中即为复合控制传递函数；Δiref为电流参考量；Ih为稳态电感电流。

考虑直流母线电压和电容电压波动比例很小，令Δud=0，Δuc=0，则

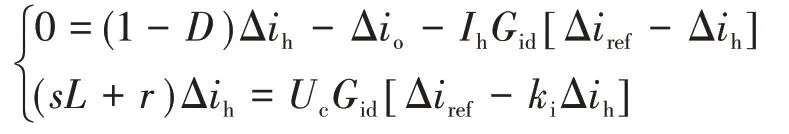
结合式（11）和式（12），可得DCES工作在Boost模式时的电流闭环控制框图，如图4所示，其中，G1为DCES频域模型。

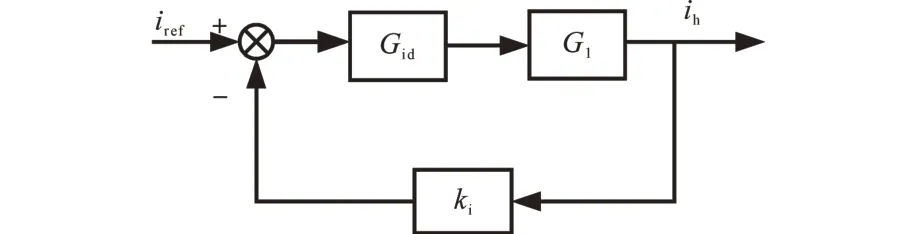
图4 Boost工作模式下控制框图Fig.4 Control block of DCES under Boost mode

同理，根据工作原理可推导出DCES工作在Buck模式下的频域模型及控制框图，其与图4所示一致。受篇幅限制，本文中不再逐一推导。

2.2 DCES复合控制

根据DCES工作原理可知，电流ih为交流量，传统的PI控制器难以实现无静态误差跟踪，而多PR控制器并联的方法较为复杂、计算量大。为此本文提出采用PI控制+重复控制（repetitive control，RP）的复合控制DCES方法。重复控制为基于内模原理的一种控制方法，通过对其内模参数的设置，可实现对某一频率及其倍数频率的交流量的无静差跟踪，其离散域内的控制框图如图5所示。

图5 离散域下重复控制原理框图Fig.5 Control block of repetitive control in z-domain

图5中，E（z）为重复控制器的输入误差的离散量；S（z）为控制器补偿函数，通常设置为二阶低通滤波传递函数；Q（z）为提高系统稳定性和鲁棒性的内模衰减函数，其通常取值为小于1的常数或一阶低通滤波传递函数；Y（z）为输出离散量。根据图5，可得出离散域下重复控制的内模传递函数为

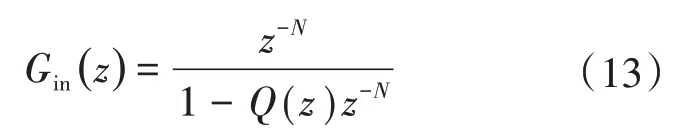
式中：N为一个纹波电流脉动周期内的采样点数。

参考文献[13]，本文中选取Q（z）=0.95。

根据式（13），分别给出重复控制和准PR控制Bode图，如图6所示。由图6可以看出，与准比例谐振控制方式比较，重复控制在基波及其周期频率出均存在谐振峰值，表明其对周期次环流谐波的均具有良好的抑制效果。此外由于重复控制和准比例谐振控制对直流偏置分量的抑制效果较差，因此，为保证DCES的稳定运行，本文提出采用PI控制+重复控制的复合控制策略。传统的复合控制为上述两种控制方式的简单并联，虽然便于参数整定，但重复控制器的补偿函数设计困难。

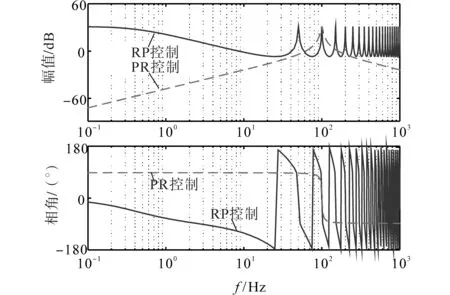
图6 准比例谐振和重复控制Bode图对比Fig.6 Comparison of quasi-PR control and RP control

对此，本文采用嵌入式结构的复合控制方式，根据2.1小节对DCES频域模型的分析，令ki=1，做出DCES整体控制框图结构，如图7所示，其中PIv（z）为稳压PI控制器的离散域传递函数。

如图7a所示，DCES的指令电流由两部分构成，其一为保证DCES电容电压稳定的稳压控制环路，另一部分为变流器直流母线电流中提取得到的低频纹波电流分量，为简化控制过程，本文采用带通滤波环节进行提取。

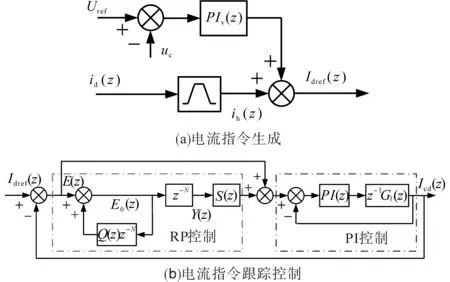
图7 DCES控制框图Fig.7 Control block of DCES

3 稳定性分析及控制参数设计

根据图7（b）所示电流环路控制框图，可以看出，在控制过程中，指令误差及重复控制输出之和共同作为PI控制器的输入。由于在暂态过程中，重复控制器需要1个周期的延时，此时控制系统的稳定性由经过前馈支路的PI控制部分决定。因此，可根据传统控制设计方法，对内环PI控制的参数进行设计。由PI控制特性可知，虽然此时PI控制无法达到无静差的调节目的，但1个周期后，重复控制发挥作用并放大控制误差，参与PI控制，当进入稳态后，输出电流即可实现对指令电流的无静差跟踪。根据图7b可得出输出与指令之间的离散域传递函数为

其中，GRP（z）为重复控制传递函数，其表达式为

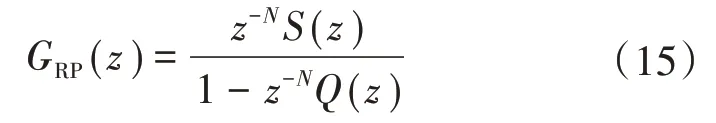
根据离散控制理论的小增益原理，为使系统处于稳定状态，离散系统的闭环传递函数的极点必须均位于单位内。式（14）所示传递函数的特征方程为

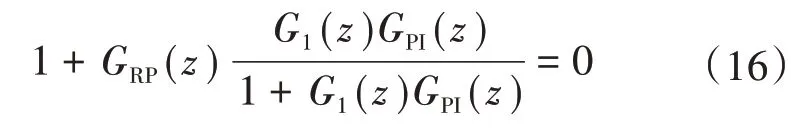
将式（15）代入式（16），整理后可得控制系统稳定的条件为

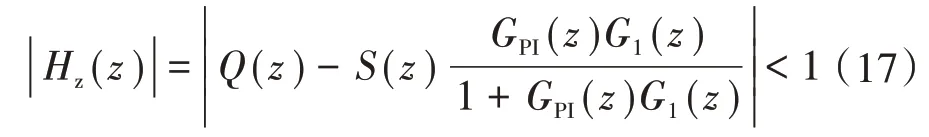
在不同系统稳定函数Q（z）情况下，根据式（17）可画出添加补偿函数S（z）前后系统稳定条件不等式的复平面关系，如图8所示，其中，ω∈[0,π/Ts]。

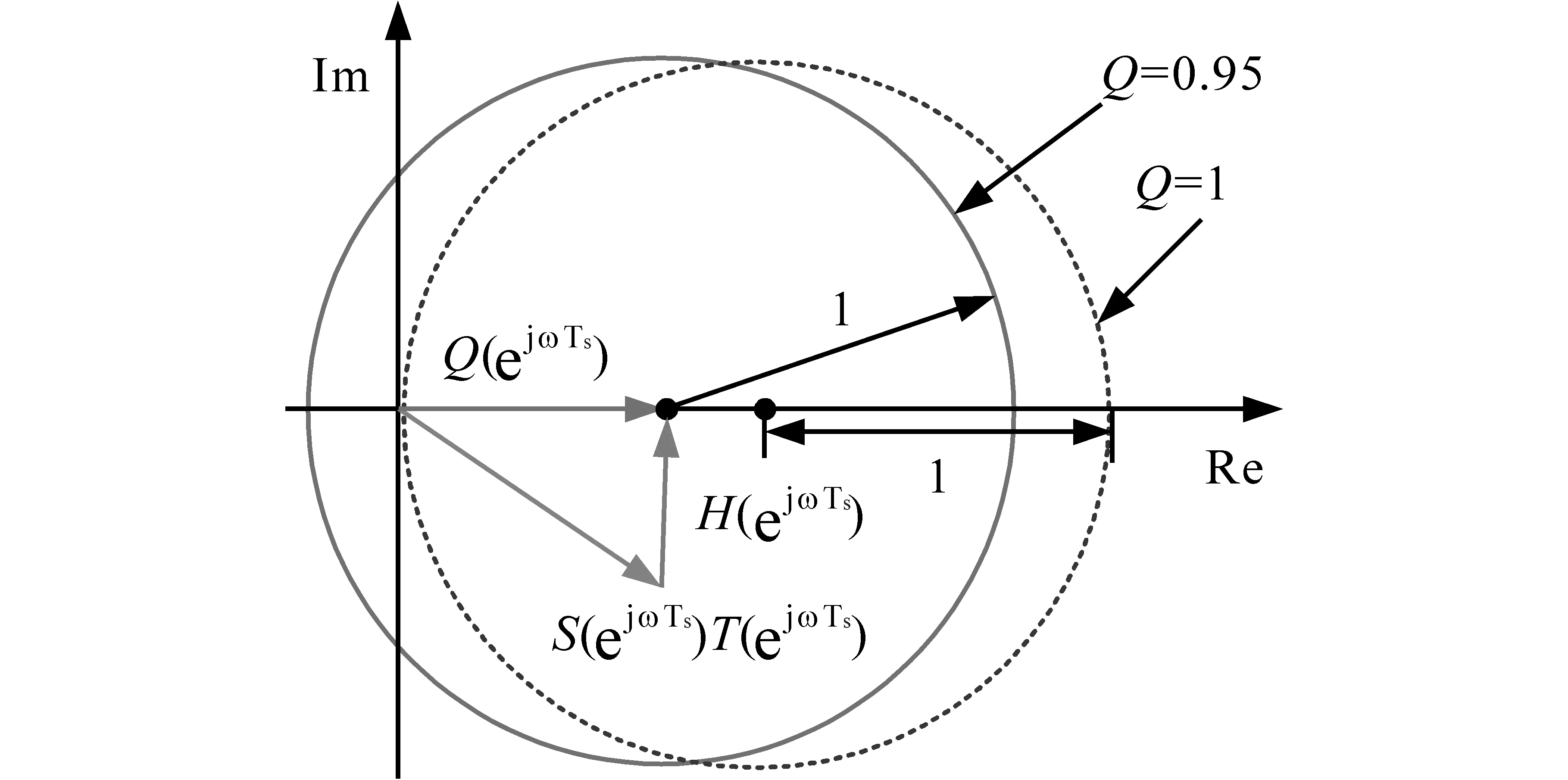
图8 复合控制的稳定性分析矢量图Fig.8 Vector diagram for stability analysis of hybrid control

由图8可以看出，当角频率ω从零增大到奈奎斯特频率时，所有特征根均被限制在一个单位圆内，系统渐进稳定。根据式（14）所示闭环传递函数特性，在高频段时，系统相位存在较大滞后，补偿器和控制对象在高频段的大幅度幅值衰减导致S（eωTs）T（eωTs）的模很小，其轨迹也可能会进入第二、第三象限内。对比取不同Q（z）时可行域与坐标轴的关系可以看出，在衰减函数取值小于1时，在系统小增益处的稳定性更好。但图7b所示控制框图表明，较小的衰减函数将降低系统的增益，控制稳态精度较差，综合考虑本文中取Q（z）=0.95。

此外，根据式（17）及图8可以看出，重复控制器的补偿函数S（z）对控制系统稳定裕度影响较大[14]。本文给定补偿函数形式为

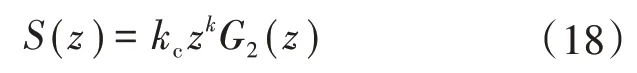
kc为重复控制前向通道增益，调节重复控制作用的强度，同衰减函数相似。

kc其取值较小时，稳态误差变大，但稳定性得到提高。因此kc需要在稳态误差和稳定性能之间折中考虑。

G2（z）对高频段的幅频特性进行矫正，主要作用为抑制高频处的干扰，为提高G2（z）衰减能力，通常设其为二阶低通滤波器，考虑补偿带宽，其截止频率应略大于待补偿环流谐波频率。考虑其高频衰减作用，本文中设定截止频率为fn=1.35 kHz，阻尼系数为ξ=0.55。离散化后表达式为

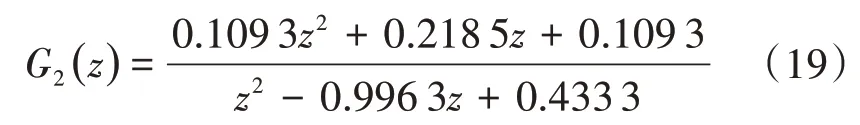
超前环节zk用来对PI控制器在中低频段的滞后相位进行矫正。图9给出了取不同k值时，补偿后zkG2（z）T（z）的频域特性，综合考虑后本文中令k=4。

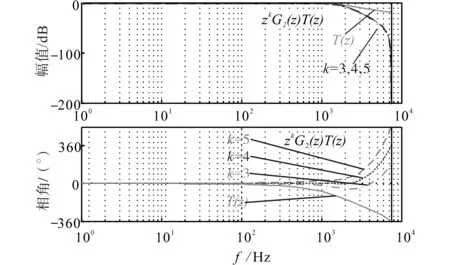
图9 补偿前后频域特性对比Fig.9 Comparison of f-domain bode diagram between with and without compensation

4 仿真及实验验证

为验证不平衡负荷下直流母线电流的频域分布以及本文所提出的有源抑制策略及其控制设计的有效性，利用Matlab/Simulink搭建了380 V储能变流器的仿真模型，其具体参数为：电网电压Un=380 V，电网频率fn=50 Hz，DCES开关频率fs=10 kHz，DCES桥臂电感L=1.5 mH，DCES电容C=2.5 mF，比例系数kp=3.6，积分系数ki=18.8。

首先，对不平衡负荷下，储能变流器的工作状态进行仿真，设定三相纯阻性负荷功率分别为5 kW，7 kW和6 kW。仿真结果如图10所示。

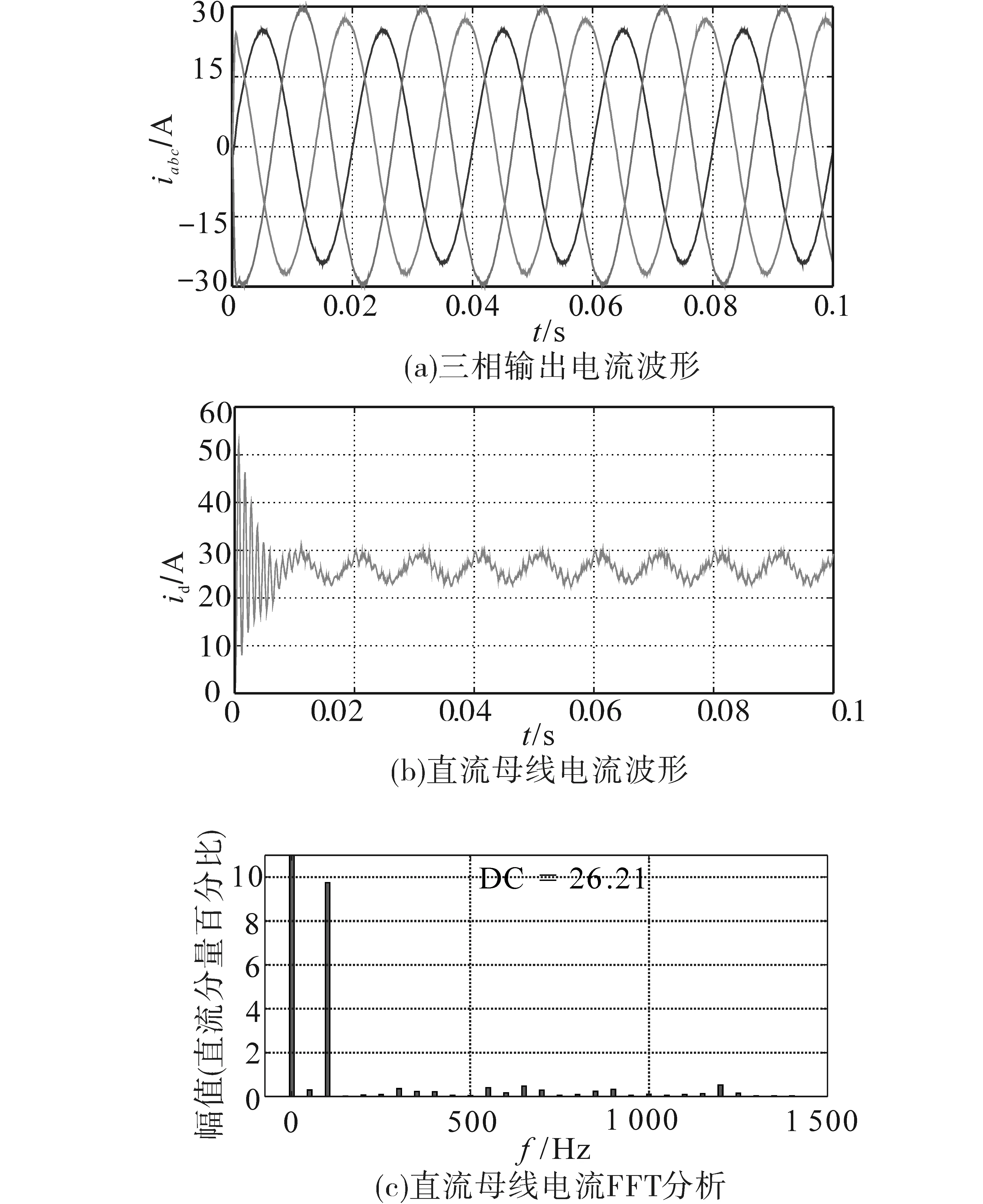
图10 不平衡负荷下仿真波形Fig.10 Simulation waveforms under unbalance three-phase load

从图10a可以看出，此时三相输出电流处于不平衡状态，而图10b显示直流母线电流存在脉动分量。对直流母线电流进行FFT分析，结果如图10c所示。可以看出，此时直流母线电流中除直流分量外还存在较大分量的两倍基波频率的电流纹波。在不加抑制措施情况下，此低频电流将直接进入电池内，造成储能电池过热。

为验证本文所提DCES的作用，在相同负载情况下，启动DCES进行仿真，并对输出相电流进行FFT分析，可得此时进入到电池的母线电流的频域分布如图11所示。

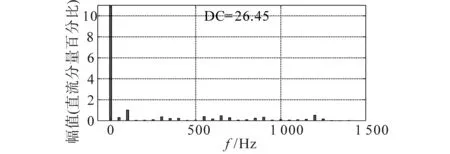
图11 DCES工作时直流母线电流FFT分析Fig.11 FFT analysis of DC current with DCES

对比图10c和图11可以看出，在DCES作用后，进入储能电池的电流中低频纹波电流分量由开始的9.7%下降至0.86%。仿真结果对比验证了DCES对直流母线低频纹波电流抑制的有效性。

在仿真模型的基础上，搭建了直流母线电压为120 V，线电压有效值为60 V，容量为2 kV·A的储能实验样机。其中，采用TMS320F28335作为主控制器，功率器件为英飞凌的MOSFETSTW56N65M2-4，通过三相逆变器输出连接不同阻值的电阻模拟不平衡负载。储能变流器及DCES的开关频率均为10 kHz。

上电后，在程序运行前期，DCES未投入使用，在某一时刻通过按键检测方式启动。实验结果如图12所示。

根据图12所示实验结果可以看出，在未接入DCES时，储能变流器直流母线电流存在较大幅值的波动，而DCES电容电压波动较小。实验结果展开图如图12b、图12c所示。与之对比，在投入DCES后，直流母线电流幅值基本维持在恒定值，波动很小，而DCES电容电压的波动幅值较大，实验结果表明，不平衡负荷引入的低频纹波脉动功率基本由DCES电容吸收，未进入储能电池。因此，实验结果验证了DCES及控制算法的有效性。

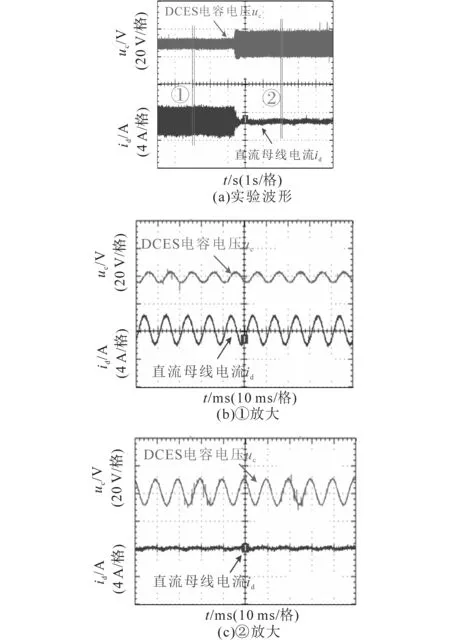
图12 直流母线电流和DCES电容电压实验波形Fig.12 Waveforms of DC-bus current and DCES capacitor voltage

5 结论

本文研究了储能变流器带不平衡负荷时，直流母线低频纹波电流问题的产生机理及有源抑制方法。利用理想情况下的两电平变流器的开关函数等效模型，推导出直流母线电流的表达式，并指出低频纹波电流与电网侧所接负荷的不平衡度成正比。随后，建立了直流电力弹簧的小信号频域模型，并针对传统PI或PR控制的局限性，给出了一种采用改进型复合控制的低频纹波电流抑制方法，并分析了控制系统的稳定性，给出了关键参数的设计原则。

最后，利用Matlab/Simulink仿真模型的仿真结果及等比例小型样机实验结果验证了本文直流电力弹簧及控制策略的可行性。