一种内嵌式永磁同步电机启动策略

郑伟杰，孙天夫，来跃深，尚雅层

（1.西安工业大学机电工程学院，陕西西安710016；2.中国科学院深圳先进技术研究院，广东深圳518000）

内嵌式永磁同步电机（IPMSM）具有高功率密度、高转矩电流比、调速范围广等特点，在新能源汽车、数控机床、机器人等领域得到了广泛的应用[1-2]。在电机启动阶段，为获取高性能的控制系统，需要检测转子角度进行磁场定向控制。传统的检测方法是安装机械式传感器（如绝对式编码器、增量式编码器、霍耳传感器等）。但机械式传感器的使用在增加系统成本的同时，也降低了系统的抗干扰性。无位置传感器控制技术通过构建位置观测器估计转子角度，避免了机械式传感器的使用[3-4]。在低速与零速时，通常采用具有强鲁棒性的高频注入法，但该方法无法判断永磁体N/S极，难以准确地获取电机转子的初始位置，导致电机启动困难[5]。

针对上述问题，文献[6]通过向d，q轴注入高频脉振方波电压信号，采用无滤波器载波信号分离的方法获取转子角度误差信号，并向d轴施加等幅反向的电流偏置，比较d轴高频电流响应幅值大小完成永磁体N/S极判断。该方法减少了带通滤波器与低通滤波器的使用，避免了高阶滤波器带来的相位延迟，但电流偏置的施加破坏了高频注入法的连续性且高频电流响应幅值大小受电流噪声影响难以准确获取。文献[7]将正交方波电压信号注入静止坐标系，利用其高频响应电流估计转子角度，再通过向d轴注入正弦电流信号完成永磁体N/S极判断。该方法直接通过求反正切获取转子角度，收敛速度快，具有良好的启动性能，但需要进行多次电流差值计算，估计精度受电流零点偏移现象影响严重。

基于以上分析，本文提出了一种内嵌式永磁同步电机启动策略。所提出的策略使用Luenberger位置观测器代替单PI调节器构成的锁相环估计转子角度，降低了转矩波动对估计精度的影响，提高了位置观测器的鲁棒性；针对基于高频脉振三角波电压信号注入法的无位置传感器控制系统无法判断永磁体N/S极的问题，采用两次转子预定位法将转子定位于零度位置（机械角度为零处），无需永磁体N/S极判断，控制过程简单易行，保证了高频脉振三角波电压信号注入法的连续性与电机启动的平稳性。最后，在Matlab/Simulink上搭建了该策略的仿真模型，仿真结果表明该启动策略稳定有效。

1 高频脉振三角波注入法原理

IPMSM在d-q坐标系下的数学模型为

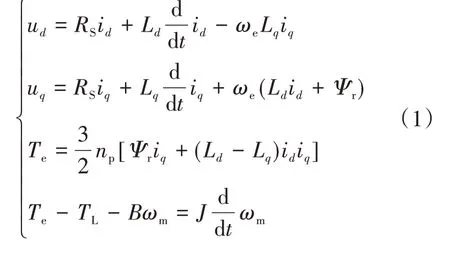
式中：ud，ud，id，iq，Ld，Lq分别为d，q轴电压、电流、电感；np为极对数；RS为定子电阻；Ψr为永磁体磁链；ωe为电角速度；Te为电磁转矩；TL为负载转矩；J为转动惯量；B为摩擦系数；ωm为机械角速度。

图1 各坐标系关系示意图Fig.1 Schematic diagram of the relationship of each coordinate system

其中 X1=(Xdh+Xqh)/2 X2=(Xdh-Xqh)/2

式中：uinj(t)为幅值是Ua的三角波函数。

图2 高频脉振三角波电压信号时序图Fig.2 Sequence diagram of high-frequency pulsating triangle wave voltage signal injection

将注入的高频脉振三角波电压信号进行傅里叶分解并代入式（2）中可得：

其中 M=4U(Ld-Lq)sin(2Δθ)/π2

Xdhn=RS+j(2n+1)ωhLd

Xqhn=RS+j(2n+1)ωhLq

ηdhn=arctan[(2n+1)ωhLd/RS]

ηqhn=arctan[(2n+1)ωhLq/RS]

式中：ωh为注入的高频脉振三角波电压信号频率；Xdhn，Xqhn分别为d，q轴第n次谐波高频阻抗，n=0,1,2…；ηdhn，ηqhn分别为d，q轴第n次谐波高频阻抗相角。

高频激励下电感阻抗远远大于电阻阻抗，因此式（4）可简化为

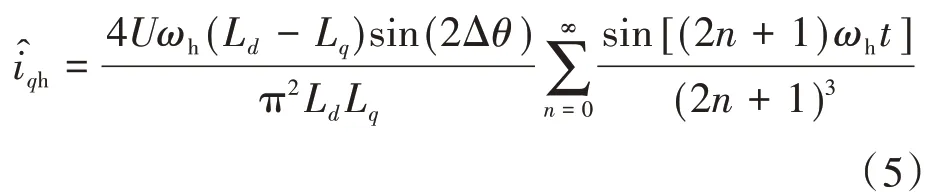
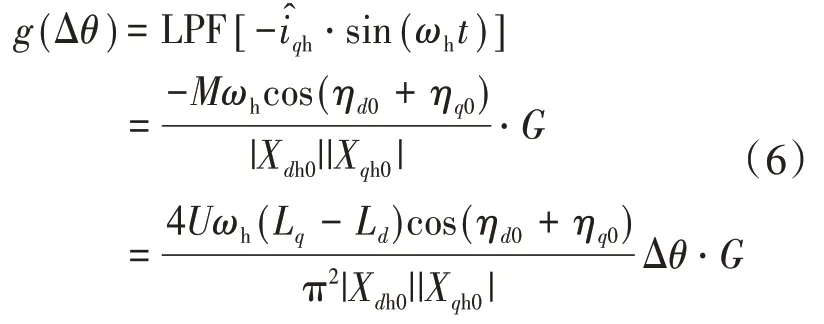
式中：G为LPF在ωh上的增益；ηd0，ηq0分别为d，q轴第零次高频阻抗相角。

式（6）中，由于LPF仅需滤除高频分量，得到含有转子角度误差信息的低频分量g(Δθ)，因此截止频率可提高至与注入的高频脉振三角波电压信号频率相同，则引起的相位滞后可被忽略。

由式（6）可知，当调节g(Δθ)为零时，Δθ也为零，即θ^收敛于θ。单PI调节器构成的锁相环收敛速度受转矩波动影响大，严重时易出现超调现象，因此本文采用基于IPMSM数学模型的Luenberger位置观测器进行转子角度估计，提高了位置观测器的鲁棒性。信号解调过程如图3所示。

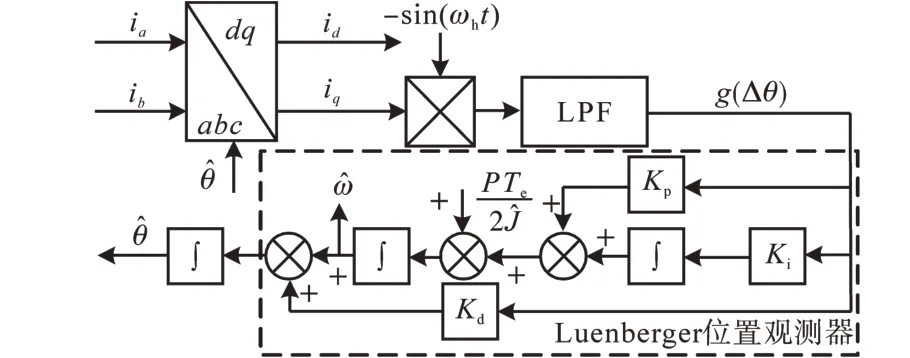
图3 位置观测器工作原理图Fig.3 Schematic diagram of position observer

图3中，Luenberger位置观测器传递函数为

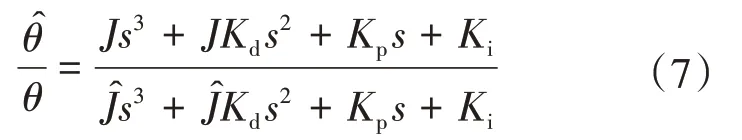
2 两次转子预定位法

图3所示的位置观测器在Δθ=0或Δθ=π时皆收敛，无法进行永磁体N/S极判断。文献[5]和文献[6]提出的永磁体N/S极判断方法虽然能够有效地识别永磁体N/S极，但向d^轴注入外部信号时都破坏了高频注入法的连续性。因此本文采用两次预定位法将转子定位到零度位置之后再进行基于高频脉振三角波电压信号注入法的无位置传感器控制，无需判断永磁体N/S极，保证了高频脉振三角波电压信号注入法的连续性与电机启动的平稳性。

转子预定位法就是向定子绕组中施加方向不变的定子电流矢量，使其产生同方向的定子电枢反应磁场，与永磁体磁场互相作用产生电磁转矩，将转子旋转于定子电流矢量的位置。

由式（1）中机械运动方程可知，电机转动需满足Te＞TL，因此会存在一个预定位盲区，且盲区大小与负载转矩成正比[10]。为了避免因定位盲区导致的电机预定位失败问题，本文采用两次转子预定位法。将转子预定位于零度位置为例，如图4所示，向定子绕组先后施加两次定子电流矢量。第1次预定位时，向定子绕组施加的定子电流矢量在d，q轴的分量为irq=A，ird=0，给定预定位转子角度θ′=-π，则第1次预定位后转子将定位至θ=-0.5π的位置，如图4a所示。第2次预定位时，向定子绕组施加的定子电流矢量在d，q轴的分量为irq=A，ird=0，给定预定位转子角度θ′=-0.5π，则第2次预定位后转子将定位至θ=0的位置，如图4b所示。

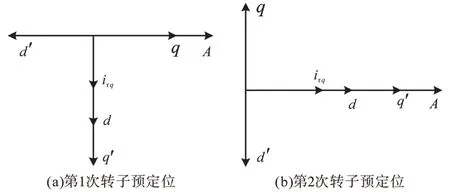
图4 两次转子预定位法Fig.4 Twice rotor reservation method

图5所示为本文所提出的启动策略工作流程图。首先，通过施加给定电流irq=A，ird=0，给定预定位转子角度θ′=-π完成第1次转子预定位；第1次转子预定位完成后，通过施加给定电流irq=A，ird=0，给定预定位转子角度θ′=-0.5π完成第2次转子预定位；第2次转子预定位完成后，转子处于零度位置，通过注入高频脉振三角波电压信号进行无位置传感器控制。

图5 所提出的内嵌式永磁同步电机启动策略流程图Fig.5 Flowchart of the proposed starting strategy for IPMSM

3 仿真实验结果

为了验证本文所提出的内嵌式永磁同步电机启动策略，在Matlab/Simulink上搭建了该启动策略的仿真模型。仿真所用的电机参数为：额定电压320 V，额定功率30 kW，d轴电感3.15 mH，q轴电感4.83 mH，定子电阻0.051 2Ω，极对数4，转动惯量0.004 3 kg·m2。注入高频脉振三角波频率2 kHz，LPF截止频率2 kHz，电压幅值50 V，逆变器开关频率10 kHz。

图6所示为电机初始位置为θ=0.5π，给定电流矢量大小50 A（irq=50 A，ird=0）时，电机所产生的电磁转矩大小。由图6a可知，在第1次预定位时，由于给定的电流矢量方向为θ′=-π，与转子位置反向，则此时的电磁转矩大小约等于零，无法迫使电机转动。由图6b可知，当第1次预定位结束后，电机仍处于θ=0.5π处，此时保持给定电流矢量大小不变，给定电流矢量方向为θ′=-0.5π，根据式（1）中的电磁转矩方程可得此时的电磁转矩大小为17.43 N·m，方向为负，可迫使电机转子顺时针旋转至零度位置。

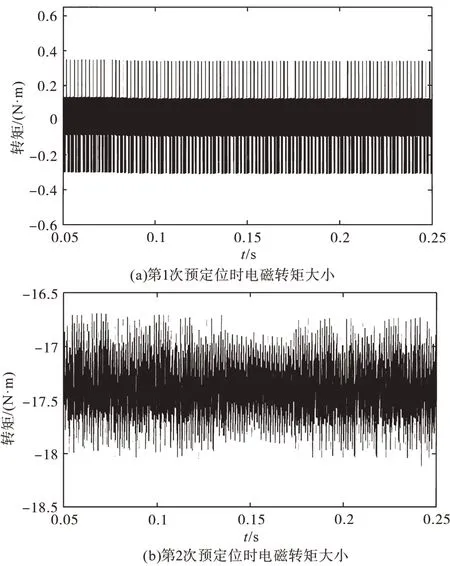
图6 转子初始位置θ=0.5π时产生的电磁转矩波形图Fig.6 Waveforms diagram of electromagnetic torque generated when rotor initial positionθ=0.5π

图7所示为电机初始位置为θ=π，给定电流矢量大小50 A（irq=50 A，ird=0）时，电机所产生的电磁转矩大小。由图7a可知，在第1次预定位时，由于给定的电流矢量方向为θ′=-π，与转子位置相差0.5π，则根据电磁转矩方程计算可得此时的电磁转矩大小为17.43 N·m，方向为正，可迫使电机逆时针旋转至θ=-0.5π处。由图7b可知，当第1次预定位结束后，电机处于θ=-0.5π处，此时保持给定电流矢量大小不变，给定电流矢量方向为θ′=-0.5π，根据电磁转矩方程可得此时的电磁转矩大小为17.43 N·m，方向为正，可迫使电机转子逆时针旋转至零度位置。

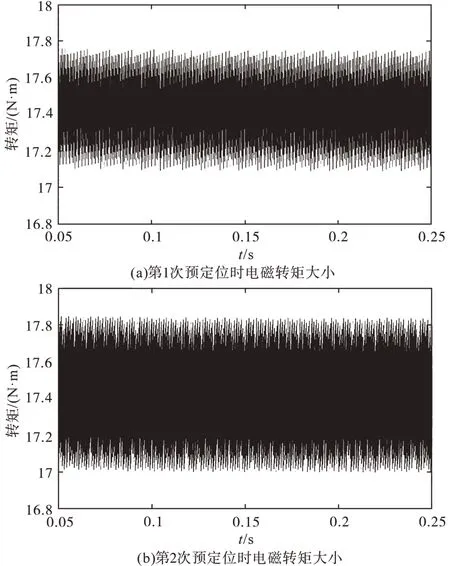
图7 转子初始位置θ=π时产生的电磁转矩波形图Fig.7 Waveforms diagram of electromagnetic torque generated when rotor initial positionθ=π

根据图6与图7可知，两次转子预定位法可有效地避免定位盲区导致的预定位失败问题，确保转子在任意初始位置都可被定位至零度位置，保障了高频脉振三角波电压信号注入法估计转子初始角度的准确性。

图8所示为电机稳定运行在ωm=20 rad/s时的仿真结果。从图8a中可知，位置观测器可精准地估计实际转子角度，收敛速度快。从图8b中可知，估计转子角度与实际转子角度误差一直稳定在0.04 rad左右，证明本文提出的高频脉振三角波电压信号注入法具有较高估计精度。

图9所示为电机稳定运行在ωm=40 rad/s时的仿真结果。从图9a中可知，随着转速的提高，位置观测器仍可有效地估计实际转子角度，无超调现象，动态性能好。从图9b中可知，估计转子角度与实际转子角度误差一直稳定在0.03 rad左右，证明本文提出的高频脉振三角波电压信号注入法在不同转速下皆具有较高的估计精度。

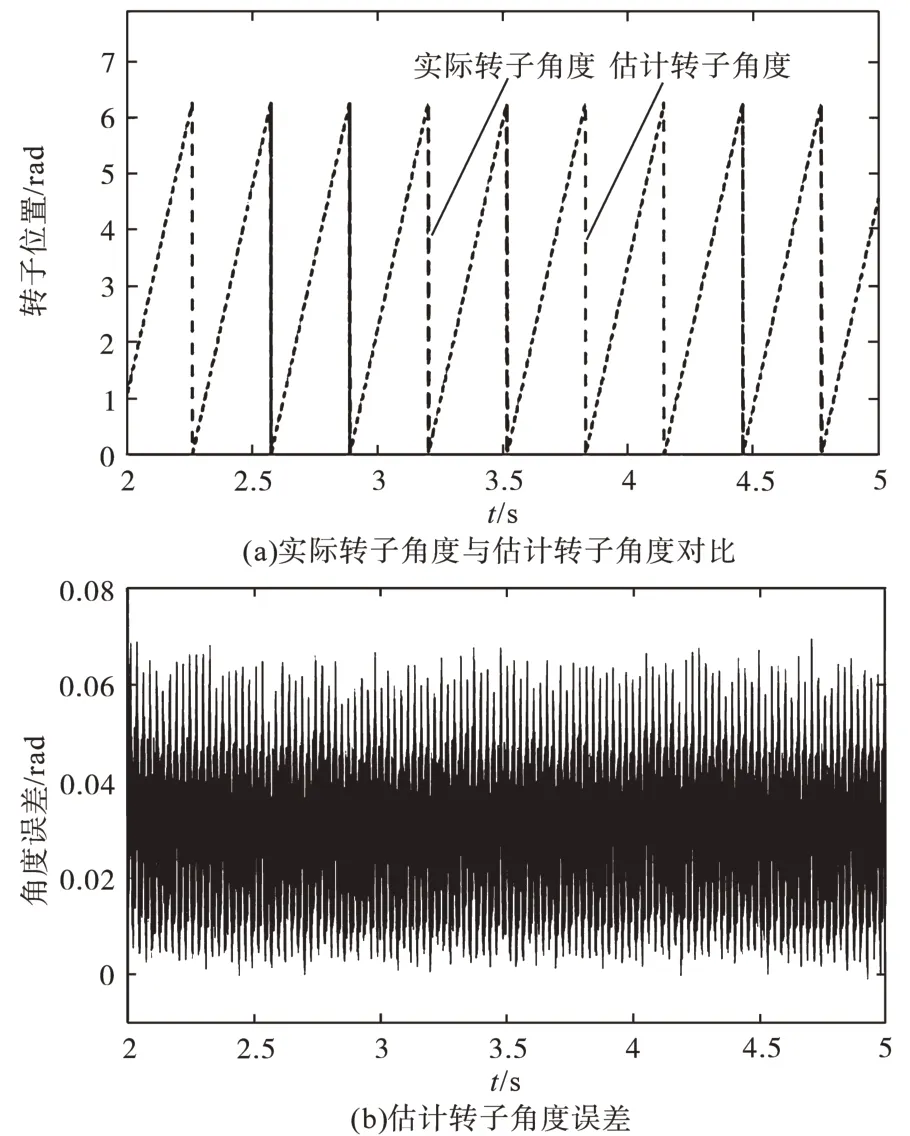
图8 ωm=20 rad/s时仿真波形图Fig.8 Simulation waveforms whenωm=20 rad/s

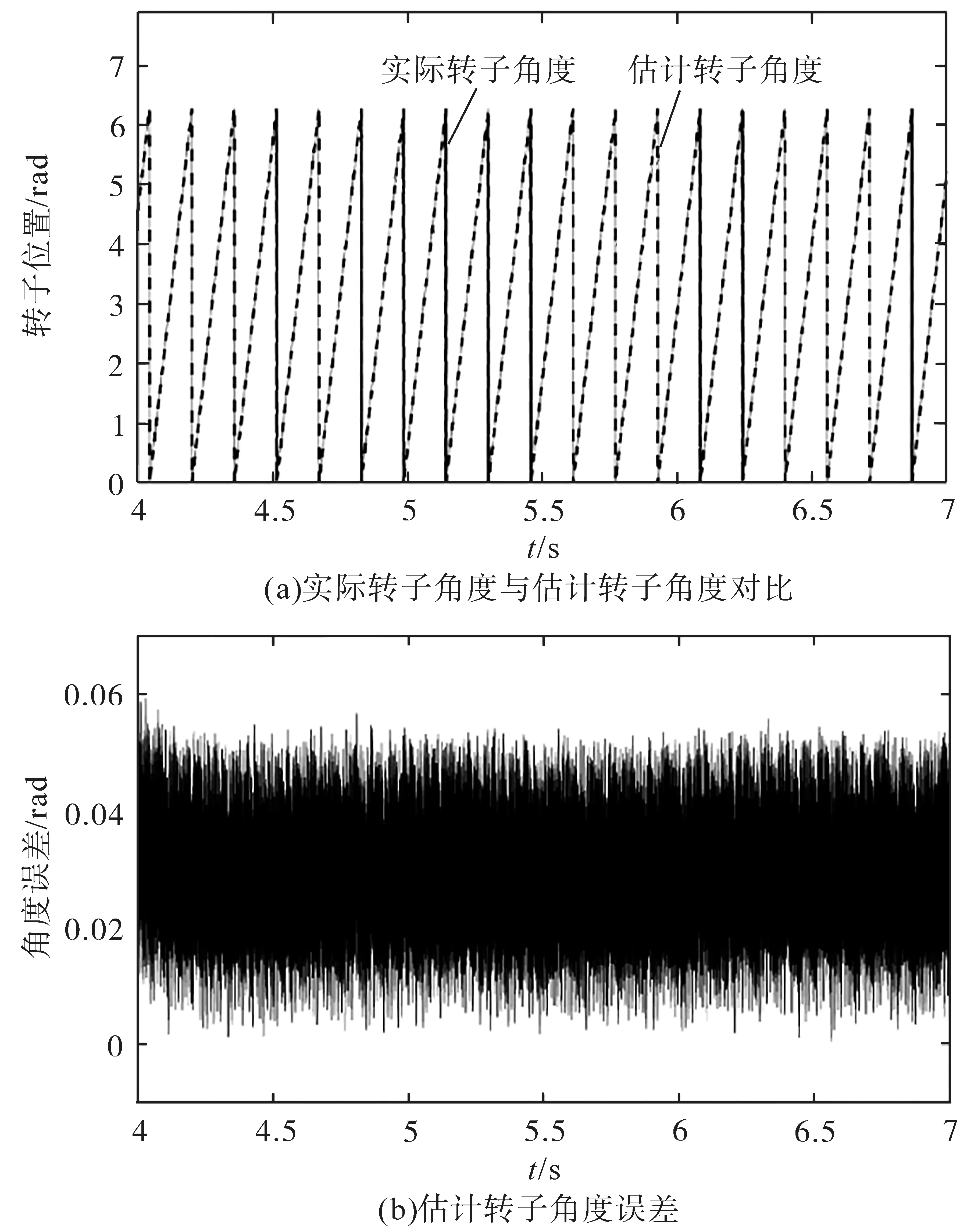
图9 ωm=40 rad/s时仿真波形图Fig.9 Simulation waveforms whenωm=40 rad/s

由图8与图9可知，本文所提出的高频脉振三角波电压信号注入法收敛速度快，不同转速工况下皆无超调现象，具有较高的估计精度。

4 结论

本文提出了一种内嵌式永磁同步电机启动策略。该启动策略通过基于Luenberger位置观测器的高频脉振三角波电压信号注入法估计转子角度；针对高频脉振三角波电压信号注入法无法进行永磁体N/S极判断问题，采用了两次转子预定位法将转子定位至零度位置。在Matlab/Simulink平台上搭建了该启动策略的仿真模型，仿真结果显示，电机转子处于任意初始位置时，两次转子预定位法皆可产生较大的电磁转矩将转子旋转至零度位置。当电机运行在不同转速下，基于Luenberger观测器的高频脉振三角波注入法估计误差都在0.04 rad左右，满足电机平稳启动的角度估计要求。综上，本文所提出的启动策略在估计初始位置时无需永磁体N/S极判断，结构简单、易实现，并具有较高的角度估计精度。