克拉茨数学问题与智能视觉时空数据应用

近期收到International Journal of Software Innovation的邮件通知，由第一作者叶洪源、通讯作者张雷共同发表的Reconstruction and Trial Verification of the Collatz Conjecture已被正式录用。该学术论文从国际数学界的克拉茨猜想入手，基于计算机“树”数据结构来构建非负整数继承十叉树模型，实现继承十叉树上的节点与非负整数对应。从理论上，定义了克拉茨-叶节点，也就是克拉茨-叶整数。经过计算发现，在继承十叉树上，当层数为800 时，所有节点都是克拉茨-叶节点；对于任意大于1 的正整数N，其由N 变换为1 的最小克拉茨变换次数为log2N，最大变换次数为800 ＊（N-1）。论文的研究成果将对多源异构数据、非线性时空数据等数据智能处理方面都有理论借鉴意义。

克拉茨猜想的魅力

1976 年的某一天，《华盛顿邮报》于头版报道了一条数学科普新闻：美国大学校园内，人们都发疯一般，夜以继日，废寝忘食地在玩一种数学游戏。这个游戏十分简单：任意取一个大于1 的自然数N，并且按照以下的规律进行变换：如果是个奇数，则下一步变成3N+1；如果是个偶数，则下一步变成N/2。

不单单是学生，许多教师、研究员及资深教授都纷纷加入。无论N 是怎样一个数字，最终都无法逃脱回到谷底1。这个问题就是著名的“克拉茨猜想”。它几乎可以说是数学史上未解问题中表达形式最简单的一个，也因此成为数学这棵参天大树上最诱人的那颗果实。

克拉茨猜想是由德国数学家Lothar Collatz于20 世纪30 年代提出。在日本，该猜想由角谷静夫教授提出，故称为角谷猜想，角谷1953 年成为耶鲁大学教授，当时被列为日本二战后“头脑外流”名单上的第一号人物。克拉茨猜想在传播过程中，收获了许多名字：3n+1 猜想、奇偶归一猜想、冰雹猜想、乌拉姆(Ulam)问题。目前，数学家们测试了几百亿亿个数，结果克拉茨猜想全部是正确的。

来自不同领域的数学家们采用数论、拓扑结构、计算数学、数理统计、微分方程与动力系统等现代数学的诸多理论试图揭开这个谜底。不少资深数学家警告称，这个问题简直有“毒”，堪称魅惑十足的“海妖之歌”：你走进来就再也出不去，再也无力做出其他任何有意义的成果。著名学者盖伊(R.K.Guy)在介绍这一世界难题的时候，竟然冠以“不要试图去解决这个问题”作为标题。密歇根大学数学家、克拉茨猜想问题专家Jeffrey Lagarias 表示：“这是一个危险的问题，很多人为其如痴如醉，但目前看真的不可能解决”。

2019 年9 月，当代最杰出的华裔青年数学家，菲尔兹奖获得者陶哲轩(Terence Tao) 给出了一份证明，表明至少对绝大部分自然数，克拉茨猜想都是正确的。陶哲轩选择合适的初始数字样本，对数字样本进行权重处理。陶哲轩使用这种加权技术得出：99%的初始值大于1000 万亿的正整数，满足克拉茨猜想。尽管这份证明不是完整证明，但已经是这个堪称有“毒”的问题上近20 年走得最远的成果。“我没指望能完全解决这个问题，但目前取得的进展已经超出了我的预期。”陶哲轩说。

大胆假设与谨慎研究

近年来，在中国科学院褚君浩院士的顾问指导下，同济大学张雷教授和微软授权资深软件构架师叶洪源共同就“克拉茨猜想”在时空大数据与光电信号等方面进行了理论重构、技术攻关和应用实践，依托浙江图元智能装备科技有限公司和同济大学上海自主智能无人系统科学中心，倾力合作，潜心研究。研究工作参照国际另一数学问题“四色猜想”，首先把二叉树数据结构加以推广，发现了非负整数十叉树，十叉树上的每一个节点和正整数唯一对应。

如果把1 看作山的谷底，N 看作山的顶峰；N越大，顶峰越高，从N 变换到1 的过程更变幻莫测。让在下山的路上，把注意力放到下一个台阶，基于这样的想法，对克拉茨猜想重新构造，提出了强克拉茨猜想：任取一个大于1 的正整数N，经m 有限次克拉茨变换，其变换结果Nm 必小于N。显然，在下山的路上，如果每次总能找到更低的下一个台阶，必定能回到山底。在数学上能严格地证明强克拉茨猜想成立，克拉茨猜想必定成立。

至此，形式简单直白，难以用数学表述的克拉茨猜想，通过重新构造并基于非负整数十叉树实现了计算机建模。在十叉树上怎样找出一条下山的路，人工智能的经典算法——迷宫路径搜索。万亿亿巨量数据的计算机处理，人工智能和大数据并没有带来期望的结果。《周期三意味着混沌》是李天岩和詹姆斯·约克在1975 年发表的，被誉为“数学文献中不朽的珍品之一”；在克拉茨变换3N+1 中，其变换系数3，似乎同样让变换结果产生混沌效应，充满偶然性。

求证似乎进入了路的尽头。一个想法悠悠地出现在脑际：是否可以把克拉茨变换次数和十叉树的层数关联起来。十叉树上一类特殊性能的节点进入视野：当其变换结果小于其初始值时，其克拉茨变换次数小于等于其层数，该类节点定义为克拉茨-叶节点。显然，克拉茨-叶节点满足强克拉茨猜想。更让人惊喜的是克拉茨-叶节点具有继承性，即克拉茨-叶节点的子节点也必定为克拉茨-叶节点。图1 为非负整数十叉树的前3 层。在第1 层上的节点2 通过一次克拉茨变换其结果为1，小于其初始数值2，所以数值2 对应的节点是克拉茨-叶节点，我们不难得出节点2 的10 个子节点02，12，22 …82 及92 也同样都是克拉茨-叶节点。继承性，这是现代面向对象计算机软件的核心思想。由此，对有限节点进行处理，得出的结论可以推广到无限的所有正整数。

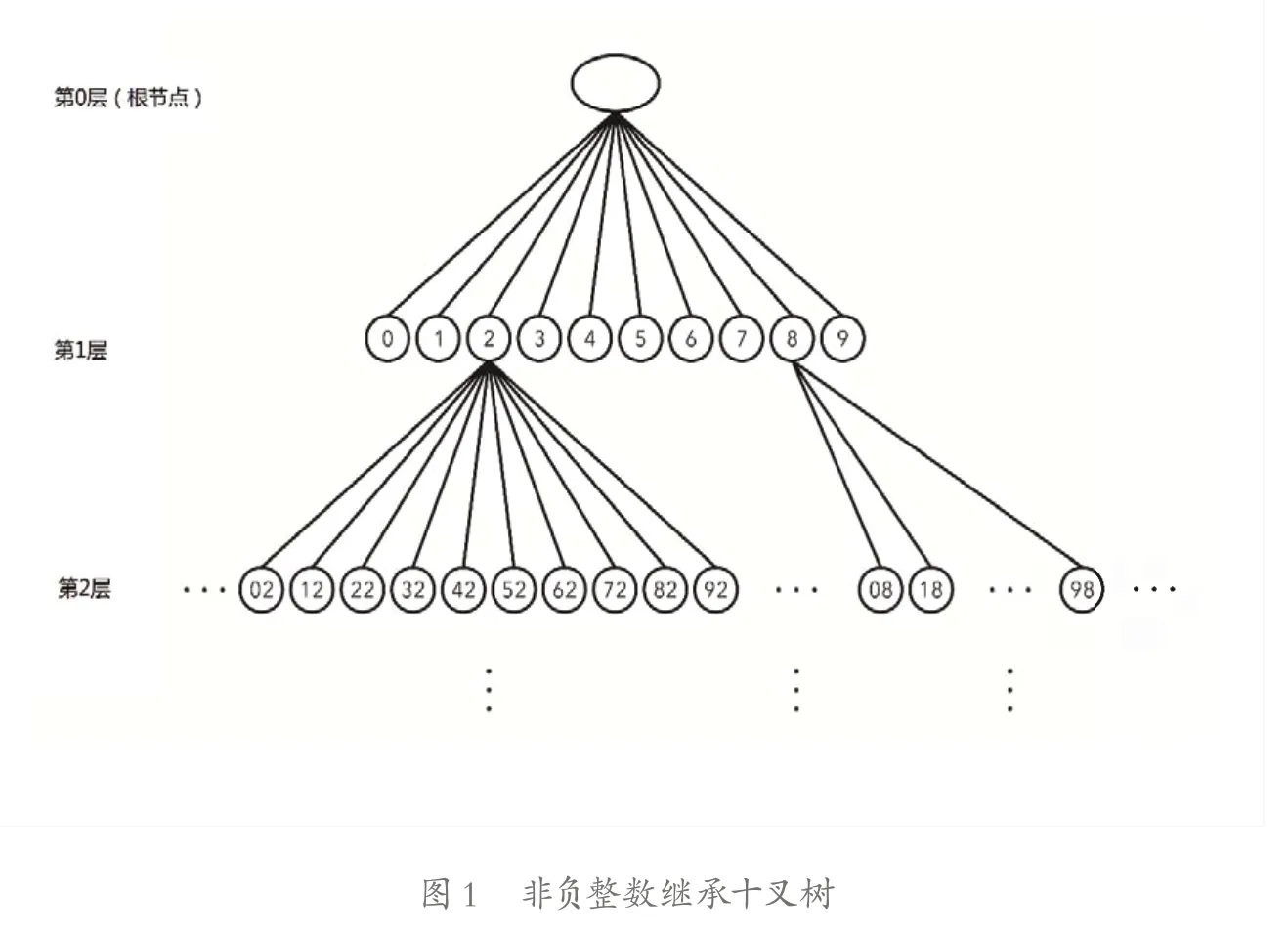
非负整数十叉树经继承性归一化处理，构建了非负整数继承十叉树。在非负整数继承十叉树对第2 层百位数计算处理，得出74.4897959% 的节点为克拉茨-叶节点，由此74.4897959% 的所有无穷多的正整数满足强克拉茨猜想；对第10 层10位正整数计算处理，得出93.7499999% 的节点为克拉茨-叶节点，由此93.7499999% 的所有正整数满足强克拉茨猜想；对第12 层12 位正整数计算处理，得出94.4824218% 的节点为克拉茨-叶节点，由此94.4824218% 的所有正整数满足强克拉茨猜想；对第100 层100 位正整数随机抽样100 亿节点计算处理，得出99.97618831% 的节点为克拉茨-叶节点，由此99.97618831% 的所有正整数满足强克拉茨猜想。

计算试证与应用验证

依托同济大学对算法、软件及其实验数据的分析与处理。在第300 层300 位正整数随机抽样1000 亿节点的计算处理中，得出99.999994779% 的节点为克拉茨-叶节点，由此99.999994779% 的所有正整数满足强克拉茨猜想。对第600 层600 位正整数随机抽样1000 亿节点计算处理，得 出99.999999997% 的节点为克拉茨-叶节点，由此99.999999997% 的所有正整数满足强克拉茨猜想。对第800 层800 位正整数随机抽样1000 亿节点计算处理，得出该1000 亿所有节点都克拉茨-叶节点，由此所有正整数满足强克拉茨猜想。该层所有节点都是克拉茨-叶节点。“上述的结论是基于随机抽样1000 亿节点计算处理得出的，并不能保证第1001 亿个节点也必定是克拉茨-叶节点。从严格的数学意义上，上述的证明结论和完全证明还有1000 亿分之一的距离。进一步的工作需要超大规模计算中心和云计算对非负整数继承十叉树进行遍历计算及处理”。该研究论文的通讯作者、同济大学张雷教授如是说。

在非负正整数十进制交叉树上，该论文对50，100，200，300，400，600 及800 层节点，分别独立随机抽样100 亿或1000 亿节点计算处理，表1为计算结果。随着节点层数的增加，克拉茨-叶节点比率也越趋近于1，在节点层数为800，克拉茨-叶节点比率为1，即在该层所有节点都是克拉茨-叶节点。

对于克拉茨猜想的证明，论文第一作者叶洪源更是感触良多。叶洪源中学时代正值改革开放之初，邓小平主持科技工作，开启了科学的春天。在那“学好数理化，走遍天下都不怕”单纯而又相对封闭的年代，徐迟的报告文学《哥德巴赫猜想》及主人公陈景润影响了整整一代人的科学理想。春天播下的种子，在科学强国的今天终于发芽结果。此次与同济大学人工智能团队张雷教授的合作，让叶洪源初尝了“科学人”的甜味。张雷教授与叶洪源的合作不仅限于兴趣性的数学问题研究。张雷教授在结束圣彼得堡彼得大帝理工大学的两年访问后，在光电信息处理方面与叶洪源开始了合作研究，探索具有多源、异构、高维、动态和海量等特征的时空数据深度学习应用领域。

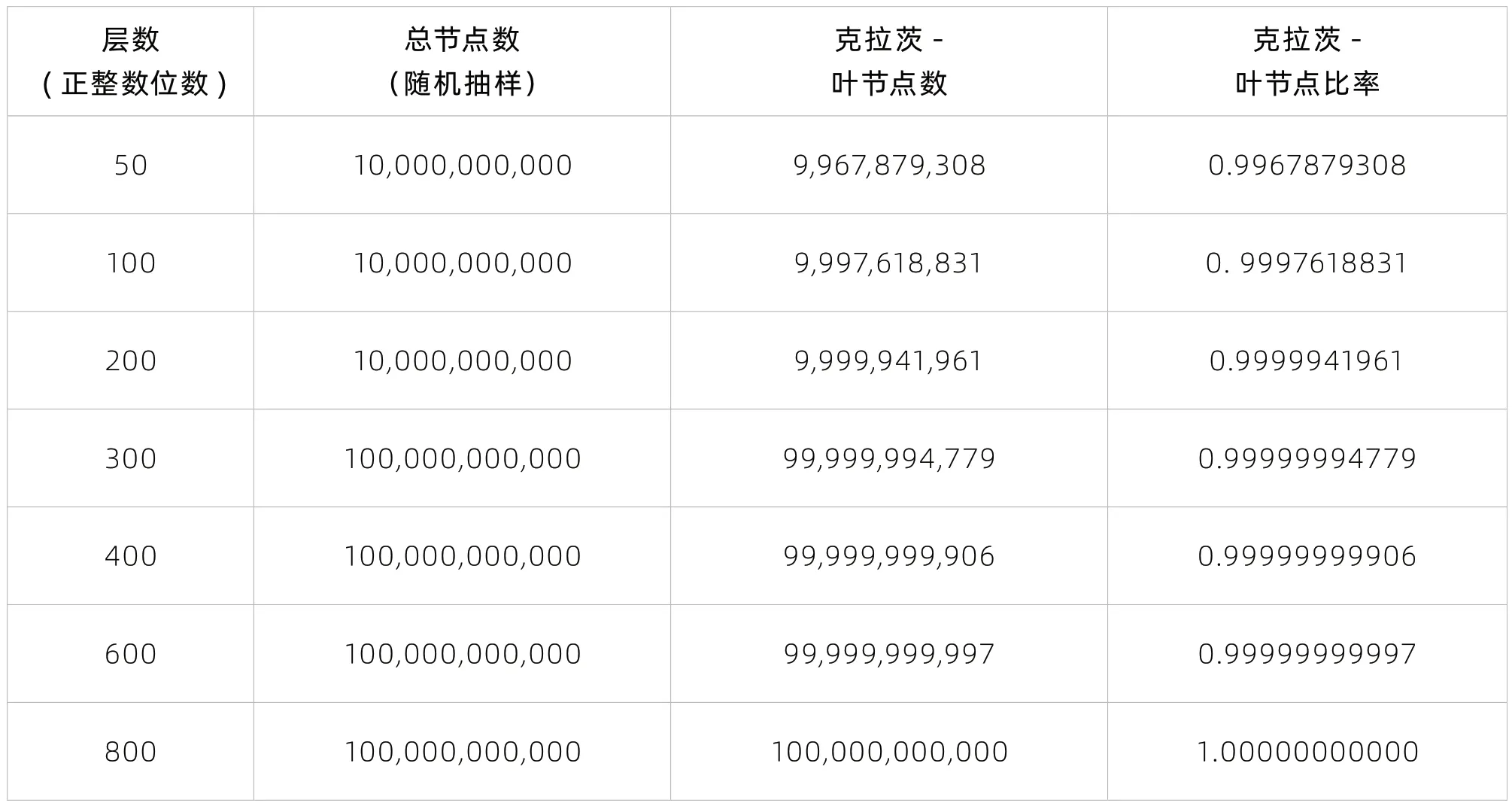
表1 大数随机抽样克拉茨-叶节点比率

基础研究是科技创新的原动力，应用导向是产学研合作的生命力。科学发现和技术发明的赋能是促进社会发展的核心使命。两位作者共同发起的“智能视觉研究中心”已经成为浙江图元智能装备科技有限公司科技创新的蓄水池。在视觉处理方面，该论文提出的“克拉茨重构”方法正在被应用中，公司正在研发“基于视觉识别的自润轴承石墨自动镶嵌系统”。自润轴承行业龙头，上市企业浙江双飞滑动轴承股份有限公司周引春董事长曾说：“自润轴承石墨镶嵌即使在日本及德国企业也是人工操作，10 年前我们就委托国内知名科研机构和国外研发团队进行开发，一直没有成功。当他们第一次找到我们计划开发该产品，我还规劝他们这个项目难度太大，不要贸然投入。过了1 年，他们把设备的工作视频展示在我的面前，我真的感到惊讶，现在我们已经向他们首批订购了5 台套。”