正交时频空:适用于高多普勒扩展场景的调制技术

徐 湛，李青宇，巩 译，孟繁轲，张校旗

(1.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192；2.北京好扑信息科技有限公司，北京 100026；3.南方科技大学 电子与电气工程系EM信息实验室，广东 深圳 518000)

为了满足未来无线通信的需求，特别是各种新业务、新场景不断涌现，第五代移动通信系统(5th Generation Mobile Communication System,5G)应运而生。高移动性案例是5G的重要应用场景之一，在高移动性和时延扩展的无线信道中实现高数据速率是IMT2020的目标[1]。高速铁路通信[2-6]、车与车之间的通信[7-12](Vehicle-to-Vehicle Communication,V2V)、车对外界通信[13-16](Vehicle to External,V2X)和无人机通信[17-20]等高移动性环境中的数据传输已被认为是未来无线通信的重要要求。而在实际应用中，高移动性场景中的通信会遭受严重的多普勒扩展，正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是目前在4G长期演进(Long Term Evolution，LTE)移动通信系统中广泛应用的调制技术，其已被应用于对抗时不变信道中的符号间干扰(Inter Symbol Interference,ISI)。众所周知，OFDM在时间不变的频率选择性信道中实现了良好的鲁棒性和较高的频谱效率。然而，对于诸如高速铁路移动通信的高移动性环境，信道通常是时变的，具有高多普勒扩展，OFDM系统在快衰落信道中容易受到多普勒效应引起的载波间干扰。因此，在高多普勒条件下，高移动性会导致OFDM出现严重的载波间干扰，从而降低信道容量[3]。

为了有效地改善OFDM调制中出现的高多普勒灵敏度问题，Hadani等[21]提出了正交时频空(Orthogonal Time Frequency Space,OTFS)调制。OTFS在时延-多普勒平面上传输信息符号，时延-多普勒平面捕获无线信道中存在的时延和多普勒频移，并能够稀疏地表示信道[22]，且OTFS可以通过在现有的OFDM系统中增加预处理和后处理模块实现传输信息符号。

通过回顾、总结国内外研究人员针对OTFS调制提出的不同方案，可以明确系统的效率和性能取决于整个通信系统。因此，应当讨论整个通信系统所有必要的细节。目前，所有的研究成果都讨论了OTFS系统的基本步骤，如信道估计、信号检测、信道均衡、分集和多址接入等，但都集中在一个具体的步骤上。因此，需要按照信道估计或信号检测等重点技术对其进行分类。首先，详细说明了OTFS系统的信道估计、信号检测、信道均衡、分集与多址接入的研究成果。其次，对时间选择性信道和OTFS基本原理进行了详细介绍。最后，总结了OTFS存在的开放性问题。

1 OTFS主要研究工作

1.1 OTFS系统的信道估计

信道估计指从接收到的信号估计信道参数，与OFDM系统中广泛使用的时频域信道估计方法不同，OTFS系统可以利用信道的时延多普勒域特性实现开销更低、效果更好的信道估计。现有文献中针对OTFS系统提出了多种信道估计技术[23-49]。Murali 等[23]提出了一种基于伪随机噪声(Pseudo-random Noise,PN)序列导频的时延-多普勒域信道估计方案，Fish等[24]使用群表示技术构造伪随机序列，能显著改善匹配滤波器算法的信道估计性能。以上两种方法均是在时频域进行信道估计，系统结构非常复杂[25-27]。

Raviteja等[25-26]利用了多径信号的叠加特性进行信道估计。针对存在分数多普勒的OTFS多径信道，提出了一种嵌入式OTFS信道估计方案，适用于具有理想脉冲整形波形和矩形脉冲整形波形的点对点单输入单输出(Single-Input Single-Output,SISO)系统。该方案在时延-多普勒网格中插入单个导频符号、保护符号和数据符号，保护符号可以适当地避免导频符号和数据符号之间的干扰，也能使信道估计和信号检测发生在同一OTFS帧内，不会产生大于帧本身的检测延迟。针对文献[25-26]的方案存在保护符号过多导致的系统容量显著下降的问题，文献[28]提出了一种基于先验信道统计的方案，在保证时延-多普勒信道下OTFS的高质量性能的同时，通过优化信道估计开销最大化系统遍历容量。针对文献[25-26]需要相对高功率的导频减小信道路径检测过程中的错误对信道估计的影响的问题，文献[29]提出了一种最大似然(Maximum Likelihood,ML)信道路径检测方法，并提供了一个最小均方误差(Minimum Mean Squared Error,MMSE)信道估计器，该方案即使在低功率导频的情况下也可以超过文献[25-26]的估计性能。文献[30]以提高OTFS系统的误码率和信道估计精度为目标，提出了一种新的导频模式，并对导频序列进行了进一步优化。首先，根据OTFS的输入输出关系推导出接收端测量矩阵的表达式，然后，根据平均互不一致性(Mutual Incoherence Property,MIP)准则，构造了以最小化平均MIP为目标的导频序列优化问题。考虑该优化问题没有闭式解，采用粒子群优化(Particle Swarm Optimization,PSO)算法求解。与文献[25-26]提出的单导频方案相比，优化后的多导频方案能够以更低的功耗获得更高的信道估计精度，同时，获得更低的误码率。

针对OTFS的信道估计问题，有研究者利用时延-多普勒域信道的稀疏性，将时延-多普勒域信道估计转换为OTFS系统中的稀疏信号恢复的问题。文献[31-32]提出了一种三维正交匹配追踪(3D Structured Orthogonal Matching Pursuit,3D-SOMP)下行链路信道估计技术，该技术能够在较少的导频消耗的条件下实现准确的信道估计。文献[33]提出的方案相比于文献[31-32]进一步降低了导频开销，提出了一种基于稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)的信道估计算法。该算法采用了文献[31-32]将信道估计问题转化为稀疏信号恢复问题的思想，再引入稀疏贝叶斯框架，将稀疏信号先验模型构造为分层拉普拉斯先验，利用期望最大化(Expected Maximum,EM)算法迭代更新先验模型的参数。文献[34]针对目前对分数多普勒信道估计研究的不足，提出了一种联合估计信道增益和分数多普勒频移的MP算法，将OTFS信道估计问题描述为一个结构化的稀疏信号恢复问题，并利用贝叶斯推理进行求解。该算法既能使用单个导频，也可以使用多个导频，并且使OTFS峰均比较于文献[25-26]显著降低。文献[35]针对毫米波大规模MIMO-OTFS系统，利用时延-多普勒角域的信道稀疏性，提出了一种基于张量的正交匹配追踪(Orthogonal Matching Pursuit,OMP)信道估计算法，并提出了一种时频域OTFS符号结构导频设计方案。基于所提的导频结构，将信道估计问题描述为稀疏信号恢复问题，并将张量分解和并行支持检测引入到基于张量的OMP算法中，降低了信号处理的维数。

袁伟杰等[36]提出一种数据辅助的信道估计方法。该方法使用整个OTFS帧传输数据，只利用一个导频符号并叠加到数据符号上传输，能实现比现有方法更高的频谱效率。针对导频与数据符号之间的干扰，设计了一种低复杂度的迭代信道估计、干扰消除和数据检测算法。该算法先通过阈值粗略地估计信道参数，再将估计的信道用于数据检测。随后，利用一种基于和积算法(Sum-Product Algorithm,SPA)的检测器，在检测到的数据码元执行干扰消除之后，用适当修改的阈值改进信道估计。袁伟杰等[37]还提出了一种基于集成传感与通信(Integrated Sensing and Communication,ISAC)信号和OTFS调制的车载网络下行传输方案。基于ISAC-OTFS信号，路边单元(Roadside Units,RSU)能够基于反射回波估计各种与运动相关的参数，如车辆的位置和速度，这些参数被进一步用于预测时延-多普勒域下行链路信道参数。因此，RSU可以产生有效地发射波束形成器，该波束形成器可以在发射ISAC信号之前补偿信道路径损耗和多普勒频移。

国内外研究者针对MIMO-OTFS系统的信道估计进行了研究。 Raviteja等[25-26]将基于脉冲的方案推广到MIMO-OTFS系统，通过在相邻脉冲之间传输多个脉冲，并在两个相邻脉冲之间设置适当的保护用以区分不同的BS天线。文献[31]基于三维结构稀疏信道将大规模MIMO-OTFS系统的下行信道估计问题定义为一个稀疏信号恢复问题。该估计器利用了在时延-多普勒域中传输的训练导频，通过在导频和数据之间插入保护间隔，接收的导频可以表示为发射导频与时延-多普勒信道的相位补偿的二维周期卷积。文献[38]利用上行训练得到的信道参数进行下行信道估计，采用基于期望最大化的变分贝叶斯(Expectation Maximization Based Variational Bayesian,EM-VB)框架恢复了各物理散射路径的上行信道参数，包括角度、时延、多普勒频移和信道增益。再充分利用上行和下行信道之间的角度、时延和多普勒互易性，重构了基站下行信道的角度、时延和多普勒频移。文献[39]利用时延-多普勒域中的脉冲作为导频进行信道估计，该方法使用单个MIMO-OTFS帧的同时估计所有发射-接收天线对的信道。文献[40]先分析了SISO-OTFS的输入输出关系，并将其扩展到大规模MIMO-OTFS，随后提出一种确定性导频设计和一种基于感知矩阵的信道估计算法(Modified Sensing Matrix Based Channel Estimation,MSMCE)，从而获取下行信道的信道状态信息。

1.2 OTFS系统的信号检测

信号检测指在接收到的原始数据和噪声数据中检测信号，信号检测是充分发挥OTFS优势的关键，已有研究者针对信号检测的内容展开研究[50-77]。消息传递(Message Passing,MP)算法是应用最广泛的OTFS信号检测算法，文献[50]和文献[52-58]采用了MP或改进了MP作为OTFS信号的检测算法。 Raviteja等[50-54]推导了未编码的时延-多普勒信道的输入输出关系，并利用信道的稀疏性提出一种低复杂度的MP检测算法。文献[55]提出了一种基于低复杂度匹配滤波的消息传递检测器(Matched Filtering Based Message Passing Detector,MF-MPD)，证明了匹配滤波OTFS信道矩阵与原始信道矩阵具有相同的结构，匹配滤波后有效信道矩阵的稀疏性保持不变。得益于匹配滤波处理，该方案可以降低复杂度和存储需求，并在低信噪比条件下获得更好的误码率性能。文献[56]利用了主成分分析(Principal Component Analysis,PCA)的优势，提出了一种基于协方差处理的近似消息传递(Approximate Message Passing,AMP)改进算法。该改进算法的复杂度与传统AMP算法相当，但误码率(Bit Error Rate,BER)性能优于传统AMP算法。文献[57]提出了一种阻尼广义近似消息传递(Generalized Approximate Message Passing,GAMP)算法。该算法基于深度学习(Deep Learning,DL)技术对阻尼因子进行优化，其每一次迭代都被展开成类似于神经网络的分层结构，并学习阻尼因子以提高检测性能。优化后的阻尼因子可直接用于原GAMP算法，而不增加其计算复杂度，该算法性能优于经典的GAMP算法和MP算法。文献[58]提出了一种联合MP-最大比合并(Maximum Ration Combining,MRC)的OTFS迭代检测方法，其MRC的集成显著提高了迭代的收敛性能，并获得了优异的系统误码性能。

袁伟杰等[59]提出了一种最大后验(Maximum a Posteriori,MAP)检测的OTFS系统的低复杂度检测器。采用变分贝叶斯方法迭代最大化证据下界(Maximize the Evidence Lower Bound,ELBO)，为每个符号产生边缘分布，从而生成低复杂度的点式MAP检测。与广泛使用的消息传递算法相比，变分贝叶斯方案的复杂度低得多，而且其ELBO最大化问题是严格凸的，可以有效地获得全局最优解，从而获得收敛保证的接收机，变分贝叶斯算法收敛速度快且检测性能优于消息传递接收机。为了降低MAP检测算法的复杂度，李双洋等[60]提出了一种划分规则。该规则根据相应的路径增益将相关的接收符号分成两个子集，用于检测每个发送符号。同时，根据划分规则，设计了利用各子集功率差异的混合检测算法。其中，MAP检测应用于信道增益较大的子集，并行干扰抵消(Parallel Interference Cancellation,PIC)检测应用于信道增益较小的子集。通过仿真得到，该混合检测算法性能接近最大后验概率检测算法，并且与现有算法相比有较大的性能提升。

Thaj等[61]提出了一种线性复杂度迭代RAKE检测器。其基本思想是利用最大比合并、等增益合并和选择合并等线性分集合并方案，在时延-多普勒网格中提取和合并发射符号的接收多径分量，以提高合并信号的信噪比。在文献[61]的基础上，Tharaj等[62]通过在时延-多普勒域中放置一些零符号，即补零(Zero Padding ,ZP)，得到了一种简化的输入输出关系，允许使用最大比合并设计低复杂度的OTFS检测器，时延-多普勒域中的这些零码元充当时域中的交错ZP保护带。利用这种交织的时域ZP，进一步提出了一种基于低复杂度时域MRC的交替OTFS检测方法。

国内外研究者针对大规模MIMO-OTFS系统的信号检测算法进行了研究[39,64-66]，并提出相应的解决方案。Kollengode等[39]采用基于MP的迭代算法进行MIMO-OTFS信号检测。首先，给出了MIMO-OTFS系统的矢量化输入输出公式，这种线性矢量信道模型能够使用各种检测算法进行MIMO-OTFS信号检测。随后，采用基于MP的迭代信号检测算法，该算法复杂度低，取得了很好的性能。Pandey等[66]提出一种在基站(Base Station,BS)基于OTFS的多用户预编码器和在用户终端(User Terminals,UTs)的低复杂度检测器(Low Complexity Detector,LCD)，解决用户终端对所有信息符号进行联合解调的挑战，所提出的LCD检测器对每个信息符号进行单独的检测。因此，具有极低的复杂度，该检测器所获得的频谱效率总和接近于在每个解决用户终端处进行最优联合解调所获得的频谱效率之和。

1.3 OTFS系统的信道均衡

信道均衡是信道估计之后的步骤，信道均衡的目的是从接收信号中去除干扰，有研究者针对OTFS系统提出了信道均衡方案[78-87]。文献[78]研究了OTFS传输矩阵的结构和特性，并针对连续多普勒扩展信道中的符号检测和干扰消除问题设计了基于最小二乘最小残差(Least Squares Minimum Residual,LSMR)的信道均衡器。该均衡器基于可靠性的动态检测器恢复传输的QAM符号，而不是采用传统的符号估计的硬判决或软判决。Surabhi等[79]提出了一种低复杂度的MMSE和迫零(Zero-Forcing,ZF)均衡器用于OTFS信号检测，不同于传统的MMSE和ZF均衡器采用的传统矩阵求逆方法。该方法识别OTFS信道矩阵的块循环特性，并利用块循环矩阵的特性显著降低复杂度，从而以更低的复杂度获得了精确的MMSE和ZF解。Pfadler等[80-81]针对不同的双色散信道，提出了不同网格和脉冲匹配的移动模式。该移动模式将自干扰控制在粗略的水平上，并通过估计导频和保护符号的剩余自干扰功率瞬时调谐线性MMSE均衡器。文献[82]提出了一种两级均衡器，将接收的信号在两个域进行处理。首先，在时频域，提出了一种滑动窗辅助的最小均方误差(Window-Assisted Minimum Mean Square Error,SW-MMSE)均衡器，有效地抑制了载波间干扰。然后，在第二级中，时延-多普勒均衡器(Delay-Doppler Equalizer,DDE)进一步减少第一级的残余码间干扰。文献[83]为了联合对抗二维干扰，采用基于线性最小均方误差的并行干扰抵消(Linear Minimum Mean Squared Error Based Parallel Interference Cancellation,LMMSEPIC)作为OTFS的均衡器。利用一阶Neumann级数近似为LMMSEPIC中涉及的OTFS矩阵求逆，将均衡器复杂度降低到与发射符号总数的准线性关系。文献[84]提出了一种基于频域预编码和MMSE均衡的自适应传输方案。首先，回顾了快衰落信道在不同领域的表示，将OTFS描述为一个更一般的预编码OFDM系统。随后，引入了一种更实用的频域MMSE均衡器，与时域MMSE和迭代均衡器如MP相比，其计算复杂度要低得多。为了优化系统性能，设计了基于信道矩阵特征值分解的预编码矩阵，以获得自适应传输。

针对MIMO-OTFS系统，Surabhi等[85]提出了适用于2×2 MIMO-OTFS系统的低复杂度线性均衡器，该均衡器利用MIMO-OTFS系统中有效时延-多普勒MIMO信道矩阵的结构所设计。MIMO-OTFS系统中的信道矩阵是由具有循环块结构的块组成，其利用了分块矩阵和分块循环矩阵的性质，降低了线性均衡器的计算复杂度。

1.4 OTFS系统的分集

OTFS系统中运用时延-多普勒网格的符号放置方式提供了信道全分集增益的潜力，OTFS调制的分集优势已在最近的研究中得到证明[88-96]。文献[90]通过接收信噪比分析研究了OTFS系统的分集阶数，并预测了OTFS有可能在时延域和多普勒域实现完全分集。Surabhi等[91]针对OTFS在双色散信道中实现的分集阶数进行了形式化分析，并给出了相应的仿真结果，证明了OTFS在信噪比趋近于正无穷时的渐近分集阶数为1。Francis等[92]研究了OTFS调制中时延-多普勒域的索引问题，提出了提高OTFS分集阶数的索引设计方案，研究了OTFS中的二维索引。其中，索引既沿时延轴也沿多普勒轴进行，证明了在OTFS中的时延-多普勒域的索引可以将渐近分集阶数提高到2。Raviteja等[93]主张使用有效分集(Effective Diversity,ED)的概念，认为在大量传输符号的情况下，有效分集比理论分集更重要。文献[93]还研究了假设矩形波形和具有两条路径的时延-多普勒信道的OTFS的分集，分析了OTFS实现QAM符号的完全有效分集的条件。由此可知，尽管OTFS的理论分集为1，但有效分集取值为2。

Augustine等[94]提出并研究了空时编码(Space-Time Coding,STC)在MIMO-OTFS调制中的应用。使用推广到矩阵的Alamouti码的结构实现OTFS中的完全发射分集，解析地证明结合相位旋转的STC-OTFS可以实现空域和时延-多普勒域的完全分集。Augustine等[94]还进一步注意到，带相位旋转的STC-OTFS很有实际意义，其即使在较小的帧情况下也能获得良好的分集性能，这使得其适合于低延迟应用。

1.5 OTFS系统的多址接入

多址接入技术的目的是让多个用户能同时接入基站，享受基站提供的通信服务，保证各个用户之间的信号不会互相干扰。针对OTFS系统的多址接入技术，已有国内外研究者展开研究[96-104]。Khammammett等[97]提出了一种在基于OTFS调制的无线通信系统上行链路中的多址方法。给每个用户终端分配时延-多普勒资源块，其在时延-多普勒域中间隔相等，将相应的时频发射信号限制到整个时频域的子域。通过将非重叠部分分配给不同用户终端，避免了多用户干扰(Multi-User Interference,MUI)。Augustine等[98]针对OTFS上行链路的多址接入，提出了一种新的在时频平面复用用户的交织方式，给用户分配了互不重叠和交织的时频资源块(Time-Frequency Resource Blocks,TFRB)进行传输。该方案被称为基于OTFS调制的交织时频多址(Interleaved Time-Frequency Multiple Access,ITFMA)方案，信道与每个用户的信号在时频域中的相乘作用确保了对应于每个用户的信号在时频平面上是可分离的，并且可以在接收机处独立地检测到。 Sinha等[99]提出一种新的基于OTFS调制的随机接入(Random Access,RA)前导码波形。先提出了一种基于时延-多普勒域中接收到的RA前导码估计用户终端和基站之间往返传播时延的方法。该估计即称为定时提前估计，被反馈给相应的用户终端，使得其可以提前进行上行链路定时，以便以时间同步的方式在基站处接收来自小区中所有用户终端的信号。

李牧野等[100-101]针对大规模MIMO系统在高移动性场景的上行链路和下行链路提出了一种路径分多址(Path Division Multiple Access,PDMA)方案。在分析了三维信道的能量分散和能量泄漏的基础上，设计了一种路径调度算法，合理地分配了用户侧的角域资源，保证了不同用户在三维立方体区域上的观测区域不重叠。通过执行调度算法，不同的用户可以独立地将各自的数据映射到调度的时延-多普勒域网格，并且在相同的OTFS块中同时向基站发送数据，而不会受到用户间干扰。

国内外多位研究者针对OTFS系统中的NOMA技术进行了研究。 Deka等[96]提出了一种基于码域NOMA技术的多用户OTFS系统，称为稀疏码分多址(Sparse Code Multiple Access,SCMA)，该系统称为OTFS-SCMA模型。推导了OTFS-SCMA系统在下行链路和上行链路下的渐近分集阶数表达式，证明了OTFS-SCMA为OTFS提供了比其他多址系统更显著的分集增益。在分集分析的基础上，提出了一种优化码字分配方案的算法。通过在下行链路和上行链路上的大量仿真，验证了所提出的OTFS-SCMA系统的性能。结果表明，Deka等提出的OTFS-SCMA系统比传统的OTFS-OMA具有更好的误码率性能。丁志国等[102]考虑了一种具有挑战性的通信场景，用户具有不同的移动性特征，如一些用户在高速移动，而另一些用户是静态的。在此基础上提出了一种结合OTFS调制的NOMA传输协议，使具有不同移动性的用户被分在一起以实现NOMA，该OTFS-NOMA协议适用于上行链路和下行链路传输。其中，复杂的发送和接收策略用于消除符号间干扰并获得多用户分集。分析与仿真结果表明，高移动性用户和低移动性用户都受益于OTFS-NOMA的应用，特别是NOMA的使用允许高移动性用户的信号在大量的时频资源上扩展，提高了OTFS的分辨率和检测的可靠性。此外，OTFS-NOMA保证了低移动性用户能够访问在传统的OTFS-OMA中只由高移动性用户占用的带宽资源。因此，该OTFS-NOMA方案提高了频谱效率，减少了时延。

2 时间选择性信道与OTFS基本架构

高移动性场景中的无线信道具有双选择性，其多径效应导致符号间干扰和多普勒频移，高多普勒频移使得信道具有高度的时间选择性，在这种场景下，当前广泛应用的OFDM系统会出现严重失真，从而降低系统容量。通过掌握信道的特征，并应用如信道估计等相应的技术，从而降低信道对系统性能的影响。因此，需要介绍时频域与时延-多普勒域中信道的表示，并介绍能对抗双选择性信道的调制技术——OTFS的基本架构。

2.1 无线信道的时延-多普勒表示

2.1.1 无线信道的传输特性

无线通信的过程中，发送端的信号会经过多条路径到达接收端，即多径效应。这种会使发送端信号到达接收端的时延不同的信道成为时间色散信道，也叫做频率选择性信道。

当无线通信双方相对位置发生变化时，频率也会随之改变，这就是多普勒效应，也称作多普勒频移。由于多径效应，发送端信号会沿不同的路径到接收端，导致发送端信号到接收端的入射角不同，不同路径的发送端信号存在不同的多普勒偏移，由此形成了多普勒扩展。5G定义的高移动场景最常见的就是高铁场景，在高铁场景下，基站位置固定，移动台位置不断发生变化，移动台发送信号与基站的角度会随时发生变化。该信号的多普勒频移的表达式为

(1)

其中：v为高铁的速率；λ为波长；c为光速；fc为载波频率；θ为高铁运动方向与基站的夹角；Fmax为最大多普勒频移。

相干时间约为多普勒扩展的倒数，表达式为

(2)

如果符号周期小于相干时间，那么在该时间内信道特性变化较小，接收端信号的幅度变化也较小，该信道被称为慢衰落信道。如果符号周期大于相干时间，在信号传输的过程中，信道特性会发生较大的变化，接收端信号的幅度变化也较大，则被称为快衰落信道，也被称为时间选择性信道。

2.1.2 无线信道的数学模型

无线信道可以由时频域与时延-多普勒域表示，假设发射端的信号会经过P个信道到达接收端，无线信道的时频域数学模型表达式为

(3)

其中：t′表示时间；f′表示频率；βp为信道增益；τp为信道p的时延；vp为信道p的多普勒频移；e表示自然对数；j是虚数单位。可以看出，无线信道的时频特性会随着信道的时延与多普勒频移不断变化。

无线信道的时延—多普勒域数学模型表达式为

(4)

其中，δ为单位冲击响应。信道的时延-多普勒域表示较为稀疏，易于接收端进行信道估计与信道校准，时延与多普勒频移是无线信道最主要的特征。因此，时延-多普勒域的信道表示非常直观。

2.2 OTFS基本概念

对时频信号进行时域抽样与频域抽样，时间轴的抽样间隔为T，频率轴抽样间隔为Δf，其中TΔf=1，抽样得到的离散信号表达式为

Λ=(nT,mΔf),n=0,…,N-1,m=0,…,M-1

(5)

时频调制的结果为X[n,m],X[n,m]表示为一个OTFS帧，一帧的持续时间为NT，占用带宽为MΔf，时频调制网格如图1所示。

图1 时频调制网格图

时延-多普勒调制网格定义为

(6)

时延-多普勒域中的信号为准周期信号，时延轴量化步长为1/NT，多普勒轴量化步长为1/MΔf，时延-多普勒调制网格图如图2所示。

图2 时延-多普勒调制网格图

一个OTFS帧包括MN个数据信息，一帧的持续时间为NT，占用带宽为MΔf。因此，一个OTFS系统参数包括N、M和T。考虑TΔf=1，T与Δf只需确定一个即可。其中，T与Δf的选择取决于信道参数，T要大于等于最大时延扩展τmax，Δf要大于等于最大多普勒频移vmax。

2.3 OTFS基本架构

OTFS调制与解调的系统架构如图3所示。

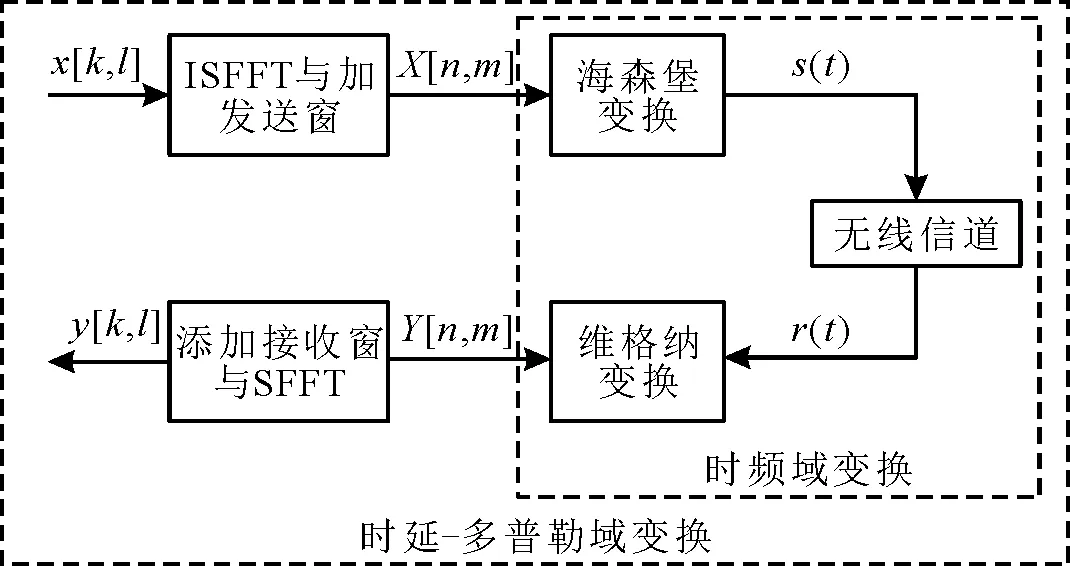
图3 OTFS调制解调框图

由图3可以看出，OTFS系统的调制解调全过程包括了OTFS调制和解调两个部分。

2.3.1 OTFS调制

OTFS调制第一步是将一个OTFS帧的M×N个数据信息映射到图2的网格中，得到时延-多普勒信号x[k,l],k=0,1,2,…,N-2,N-1,l=0,1,2,…,M-2,M-1。随后，x[k,l]经过逆辛-傅里叶变换(Inverse Symplectic-Finite Fourier Transform,ISFFT)转换至时频域，其表达式为

(7)

其中，X[n,m]为时频域信号。对时频域信号加发送窗Wtx[n,m]得

(8)

时频域调制使用发射脉冲gtx将时频域信号转为时域，该过程被称为海森堡变换，表达式为

(9)

2.3.2 OTFS解调

接收到的信号的表达式为

r(t)=∬h(τ,ν)s(t-τ)ej2πν(t-τ)dτdν+n(t)

(10)

其中：lτi与kνi为整数；κνi为分数，用于表示第i条路径的时延与多普勒频移的指标，且κνi∈[-1/2,1/2]，用于表示距离最近的多普勒分数偏移；采样时间1/MΔf近似于典型宽带系统中最近采样点的路径时延[105-106]，不需要考虑分数时延。

接收端利用匹配滤波器获得接收信号，此过程称为维格纳变换。分两步进行，第一步，计算r(t)与接收脉冲的互模糊函数为

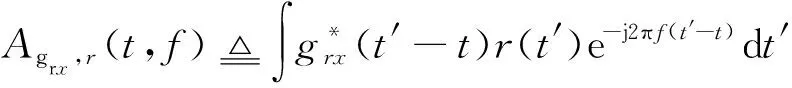
(11)

其中：grx(t)为接收脉冲；*表示共轭。

第二步，对第一步的结果以间隔t=nT,f=mΔf进行抽样，其表达式为

Y[n,m]=Y(t,f)|t=nT,f=mΔf

(12)

加接收窗Wrx[n,m]后，式(12)可表示为

Y[n,m]=Wrx[n,m]Y(t,f)|t=nT,f=mΔf

(13)

使用辛-傅里叶变换(Symplectic-Finite Fourier Transform,SFFT)将Y[n,m]从时频域变到时延-多普勒域，其表达式为

(14)

3 OTFS需要解决的问题

3.1 峰均比

峰均比可以表示为最大峰值功率除以平均功率的值。OFDM存在一个主要问题是峰均比高，其是多载波调制，所有子载波信号的叠加会导致峰值功率比平均功率高得多。OTFS系统与OFDM系统一样，具有较高的峰均比。高功率放大器由固态器件组成，其输入输出特性是非线性的[107]，高峰均比会加剧高功率放大器的非线性失真，降低通信系统的功率效率[108-111]。

Surabhi等[112]对OTFS的峰均比进行了详细的数学分析，峰均比随OTFS中多普勒抽头数目N的增加而增加。考虑了N×M延时多普勒网格上的调制符号，其中N和M分别是多普勒和时延网格数。推导出了峰均比的解析上界，这一界限与多普勒网格的数量N线性增加，即等效地为时频域中的子载波的数量线性增加，与峰均比随M线性增长的传统多载波波形不同。因此，与具有M个子载波的多载波系统相比，具有N

虽然当N较小时OTFS峰均比较低，但随着N值的增加，OTFS和OFDM的峰均比基本相同[113]。然而，在OTFS的研究中通常假设N较大，从而可以忽略检测器中的分数多普勒效应，降低了算法的复杂度[114]。因此，高峰均比仍然是OTFS中的一个主要问题。

3.2 分数多普勒

在OTFS中，时延域的偏移和多普勒域的偏移在DD域离散。一般而言，宽带系统能够提供足够的延迟分辨率，不需要考虑分数延迟偏移[105]，但多普勒分辨率取决于OTFS块的持续时间。为了满足未来通信的低延迟要求，OTFS块的时间持续时间应该相对较小。因此，必须考虑分数多普勒偏移，以避免由于假设整数多普勒偏移而产生的显著建模误差[34]。

目前，针对OTFS系统的信道估计和信号检测等方面的研究大多只考虑整数多普勒，当不考虑分数多普勒时，算法复杂度大幅度降低。若通过增大多普勒抽头数，可以减小分数多普勒的影响，从而忽略分数多普勒效应，但又会导致OTFS系统峰均比增大，加剧高功率放大器的非线性失真，降低通信系统的功率效率。因此，处理分数多普勒也是OTFS系统的主要问题之一。

3.3 基带脉冲

目前，很多研究已经使用理想的基带脉冲形状分析了OTFS性能，理想脉冲能使OTFS系统不存在ISI，使时延-多普勒域输入输出关系变得简单，从而易于进行接收机的设计。但是，考虑海森堡不确定性原理，理想脉冲是不可能在实践中实现的。因此，一个具有挑战性和开放性的问题是为实际的OTFS系统开发有效的接收器，这些系统必须依赖非理想的脉冲形状进行传输[106]。

4 结语

5G乃至6G通信的一个重要应用案例是高移动性通信场景，如高速列车通信和卫星通信。然而，在高移动性的情况下，考虑时变信道的多普勒扩展，OFDM可能会存在显著的载波间干扰，从而严重降低系统性能。为了解决这个问题，Hadani等提出了OTFS调制。首先，综述了OTFS领域国内外几乎所有的研究工作，介绍了OTFS发展概况，从信道估计、信号检测、信道均衡、分集以及多址接入5个方面详细阐述了OTFS的研究成果。其次，对OTFS的基本原理以及输入输出关系进行了分析总结。同时，对比了OTFS与OFDM。最后，介绍了OTFS的峰均比、分数多普勒和基带脉冲等几个开放性问题。