强化问题探究 促进“深度学习” 发展核心素养——由一道“解三角形”试题的探究教学引发的思考

郑 良 (安徽省合肥市第四中学 230000)

在当前的数学教与学中，不少教师反复评讲若干例题与习题，学生不断演练大量的试题，结果却只有少数学生解题时能辨识部分数学模型，实现“对号入座”，更多学生产生机械操练的熟能生笨、望文生义等后果.简而言之，学生的“四基”与“四能”并未得到显著的提高.其中的原因是多方面的，如师生不重视概念的学习和理解导致教与学中“掐头去尾烧中间”，而没有充分发掘试题资源，未能做到题尽其用更是主要的原因.布鲁纳说过：探索是数学的生命线，没有探索就没有数学的发展.要使全体学生都能主动地得到发展，就必须使全体学生都能参与到探究新知的过程中，为他们创设一个独立思考的空间.本文以一道“解三角形”试题为例，通过追根溯源、提出合适的问题，让学生从不同的角度认识数学中的同一个对象，实现全方位、多视角、立体式的研究与学习，使试题在平凡中见真奇，朴实中显能力，促进学生“深度学习”，演绎探究教与学的精彩，从而促进学生数学学科核心素养的提升.

1 案例剖析

例在△ABC中，内角A，B，C的对边分别为a,b,c，已知cos2A=sin2B+cos2C+sinAsinB.

(1)求角C的大小；

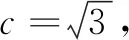
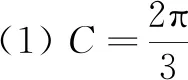
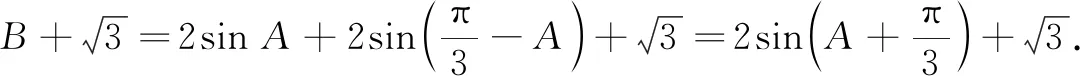
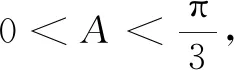
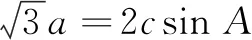
(1)求角C；

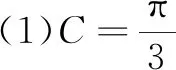
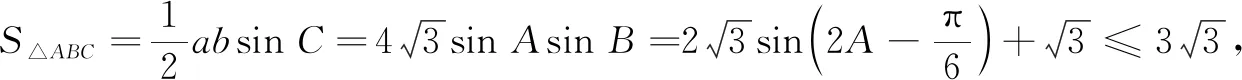
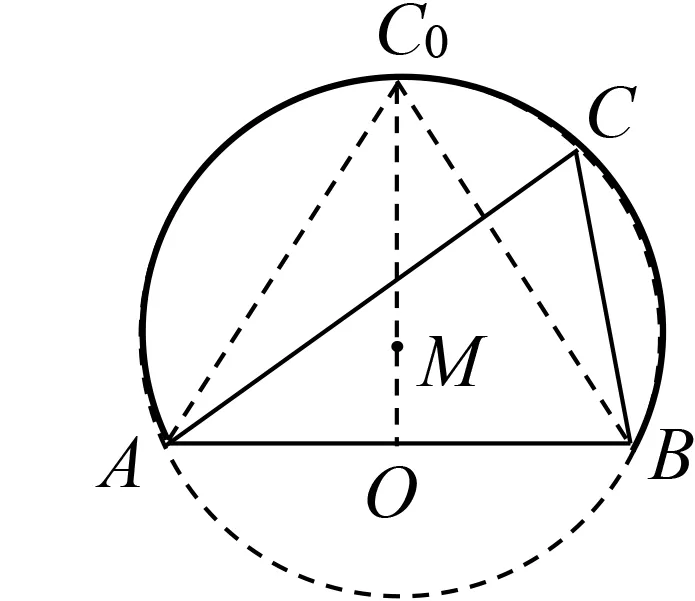
图1

例题及其变式这两个问题中，已知条件为△ABC的一边c和它的对角C，分别求△ABC的周长与面积的取值范围(或最值).由于变式求解目标为△ABC面积的最大值(特殊性)，只需满足函数最大值的定义即可，方法1是求函数取值范围的通性通法，方法2只关注函数的最值从均值不等式角度切入，方法3在动静中转换，揭示出问题的几何背景.从求解过程可以看出，当点C从点B按逆时针方向向C0运动时，△ABC的周长与面积逐渐增大，当点C从点C0逆时针向A运动时，△ABC的周长与面积逐渐减少，且当点C与C0重合时，△ABC的周长与面积取得最大值.以上结论是否具有一般性呢？周长与面积的单调性能否保持一致？为什么？

探究1在△ABC中，已知一边c和它的对角C，求其周长l和面积S的取值范围.

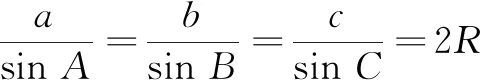
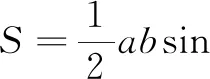
探究2在△ABC中，已知一边c和它的对角C，周长l和面积S关于A∈(0,π-C)的单调性相同.

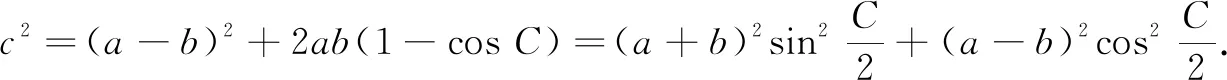
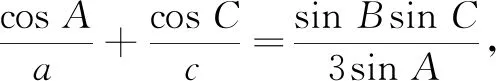
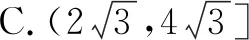
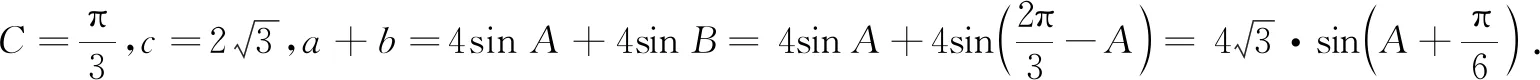
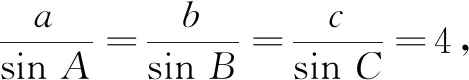
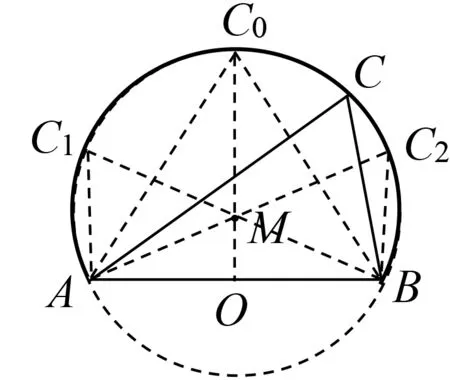
图2

评注例题与变式1分别聚焦于△ABC的周长范围与面积最大值，通过数学抽象，建立“已知△ABC的一边c和它的对角C，求其周长l和面积S的取值范围”的数学模型.通过数学运算，探究1与探究2给出(已知一边c和它的对角C)△ABC的周长l和面积S与内角A的变化关系和(海伦公式直接反应了面积与周长的关系)变化一致性，使学生实现从直观想象到逻辑推理的认知过程.例题与变式1着眼于问题的整体，而变式2则关注问题的局部.

2 教学思考

2.1 强化专业素养，提高教学能力

当前教学中存在着“不考不教，不教不研”的现象，点对点的教学真的精准吗？例题及变式中涉及“同弧所对的圆周角相等”，部分教师对此熟视无睹.在高考数学全国卷“三(几何证明选讲、坐标系与参数方程、不等式选讲)选一”时期，教师往往直接排除平面几何，导致其对平面几何基础知识与基本技能生疏.

笔者曾与部分教师交流，他们对“概率中的或然性”“立体几何(平面几何)作辅助线的灵活”“圆锥曲线中的数学运算”“导数的函数构造”等难题心中没底，教学中强化“基本套路”，通过通性通法让学生确保基础分，至于高超技巧全靠学生天分与临场发挥.笔者认为“基本套路”与特殊技巧并不对立，它与解题者基础知识的储备、解题经验的积累、解题技能的熟练程度等息息相关，通过培养，可以让学生理解知识、提高能力并提升素养.登高才能望远，教师要避免简单的重复，灵活地驾驭课堂，必须掌握与教学相关及教学以外的内容，这就要不断地学习.

2.2 强化问题探究，促进学生参与

教学中(尤其是试卷批阅后)经常听到教师抱怨：学生的基础越来越薄弱，钻研劲头不足，优化意识不强，优化能力不够.对于学生为什么上课听懂了考试却不会做题，罗增儒教授曾做了一个开车的比喻：“学生在课堂上听懂了就相当于使用导航开车，从起点到终点步步都有正确路线的指导，每到十字路口都有左拐、右拐或直行的提示，所以能很顺利地到达终点.因此，解决问题的办法之一是：平时就要锻炼‘无导航开车’，提高学生的素养.”[1]多数教师课堂教学时不敢放手，生怕学生犯错，影响教学进度.教师抢先的提示与点拨剥夺了学生独立(深度)思考的机会，越位的纠错侵占了学生自查自纠的时空，看似扩充了教学容量、加快了教学节奏，实则降低了教学效率.

每个人都能在自身基础上做力所能及的探究.教师与学生首先要有探究的意识，其次要具备探究所必备的基础知识与基本技能并掌握常见的探究方式，再次要有思维变通的能力，最后还要有锲而不舍的探究精神.探究的源头在哪里？首先要多做，从诸多事物中发现共性现象；其次要多想，可探寻解题的方式方法和一般性的结论，改变条件或结论生成新的问题.最后要多用，实践是检验真理的唯一标准.通过查缺补漏来完善认知，实现对结论的拓展.师生对以上例题与变式可谓耳熟能详，但对其认知支离破碎、不成体系，更谈不上形成数学综合素养.通过教师的合理设计，充分创设问题情境，引导学生进行探究，静等花开，相信每个学生都会有不同的收获与感受.