基于网络结构的大坝管理评价方法研究

曾昭诚，周志维

（1.江西省吉安市白云山水利水电管理局，江西 吉安 343009；2.江西省水利科学院，江西 南昌 330029）

0 引言

水库管理是一项综合性的工作，管理水平的高低直接影响水库的功能效益发挥及使用寿命，因此，合理评价水库管理水平是提升管理水平的前提条件，也是践行当前“水利工程补短板、水利行业强监管”总基调的重要方面。一般而言，管理指标体系采用递阶层结构，采用线性加权的方法进行评价，该方法是基于各元素之间相互独立、未考虑相互影响关系，实际上，各元素之间存在千丝万缕的联系，简单的线性加权进行评价可能存在偏差，难以准确的描述管理水平。因此，有必要对水库管理评价方法进行研究。

管理作为系统理论范畴，通过判断管理元素的重要性，采取针对性的措施，以达到提高管理效率的目的。管理元素的重要性可用权重大小来描述，权重越大，工作越重要。因此，科学合理的计算元素权重值，并进行排序，是首要问题。目前，在分析元素及决策领域，相关理论研究与方法相对完善，Bashiri等[1]提出了交互式线性分配法决策方法；Bertolini等[2]提出了层次分析（AHP）决策方法，该法能将决策问题构建成类似于系谱树的层次结构，通过两两比较得到判断矩阵，然而该法在构建判断矩阵是基于各元素之间相互独立的前提下，与管理元素相互影响不相适应，影响了决策的可靠性；在分析元素存在相互影响关系的方法中，主要有模糊积分法和网络分析法（ANP）[3]两种，模糊积分法存在模糊测度难以确定的局限，网络分析法是基于AHP下，并分析各指标之间相互联系的多因素评价方法，该方法适用于分析复杂结构且不易量化的评价问题[4]，在处理水库管理模糊问题时，具有一定的局限性。

在已有评价方法的基础上，采用三角模糊数来构建判断矩阵，建立基于网络分析法的模糊综合评价模型（以下简称F-ANP法）[5]。该方法已在风险决策等领域中得到发展及应用[6，7]，将其应用于水库管理评价中，可丰富水库的管理评价理论，为科学合理进行水库管理评价提供技术手段。

1 F-ANP法的基本思路

1.1 ANP网络结构

ANP结构分为控制层和网络层。以管理水平作为单一目标，控制层仅为管理等级[8]，因此，在建立ANP网络图时，仅考虑网络层。根据国家对水库的管理要求，水库管理体系由5个主要元素集组成：管理基础、安全管理、运行管理、维养管理、保障管理，编号分别为C1～C5。其中，管理基础C1包括机构人员、管理手册、注册鉴定、管理设施、工程划界、档案管理等6个元素，编号分别为e11～e16；安全管理C2包括责任人、安全生产、应急管理、防汛度汛等4个元素，编号分别为e21～e24；运行管理C3包括工程检查、工程观测、运行操作、调度运用等4个元素，编号分别为e31～e34；维养管理C4包括维修养护、设备保养、库区管理、工程形象等4个元素，编号分别为e41～e44；保障管理C5包括信息化水平、考评激励、管理经费等3个元素，编号分别为e51～e53。各元素之间的存在内在联系，其网络结构如图1。

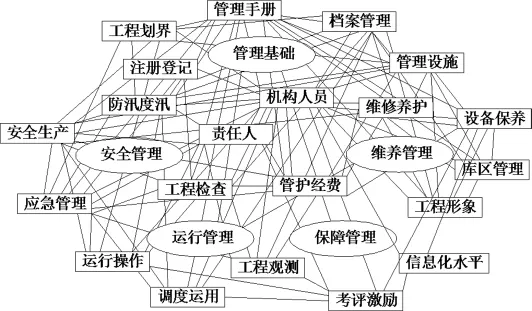
图1 水库管理元素网络结构

1.2 确定权重

各元素的权重是影响决策合理与否的关键所在。由于网络层的元素集仅有5个，且相对独立，权重的确定可由层次分析法确定，而网络层元素之间的依存关系，计算步骤如下：

1）对于元素集 C1，C2，…，C5，假定元素集 Ci中有 m个元素 ei1，ei2，…，eim，Cj中有 n 个元素 ej1，ej2，…，ejn，其中m，n由1.1节的网络结构确定。

在使用两两比较法进行判断时，当判断矩阵一致性检验不通过时，需要重点对指标进行两两比较，增加了工作量。因此，采用三角模糊数来构造[9]，用M=（l，m，u）表示。在以Ci元素集下的元素ejk（k=1，2，…m）为准则条件下，对Cj元素集下的元素进行比较，判别矩阵可表示为：

式中：（lp，mp，up）表示第 p 个专家的意见，up-lp为评判区间，反映专家在元素间相对重要程度，值越大，不确定性越大，反之亦然。矩阵中eik准则下的特征值为。

同理，以其它元素作为准则，相应归一化特征向量，则获得以Ci各元素下为准则下特征向量Wji，并表示为：

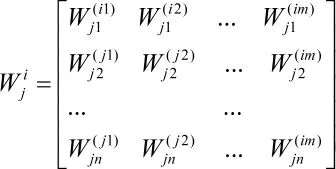
同样地，分析其它元素集Cj特征向量，最终获得超级矩阵：

该超级矩阵是非负矩阵，但不是归一化矩阵，对各元素集Cj的重要性进行比较，求得加权矩阵A：

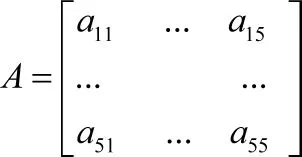
将W与A矩阵相乘，得加权超级矩阵W=A×Wij。矩阵中包含了各元素的相互影响关系，难以直接判断权重的大小，需要计算极限超级矩阵。根据极限超级矩阵存在的基本定理[1，8]，当 Wt在 t→∞ 时收敛，即：

1.3 模糊关系矩阵

确定模糊关系矩阵需要明确因素集、评价集及单因素评价矩阵。因素集即网络层下的各元素集合，评价集是各层指标的评语集合。目前，水库评价等级划分为5级，具体为：

进行单因素评价，可选取熟悉水库管理的专家，利用德尔菲法[1，10]，以问卷调查的形式，建立模糊关系矩阵R，即从U到V的模糊关系变换。

1.4 模糊网络综合评价

表1 四种算子的主要特征[1，11]

最后，按最大隶属度原则确定总体评价结论。

1.5 F-ANP法计算步骤

F-ANP法结合了德尔菲法、模糊综合评判法和网络分析法等多种方法[1，13]，通过构建模糊关系矩阵，分析评语集及因素集。在考虑各因素集的权重时，考虑了各因素之间的内在联系，并将各元素的权重进行重新分配[1，12]，计算步骤如图 2。

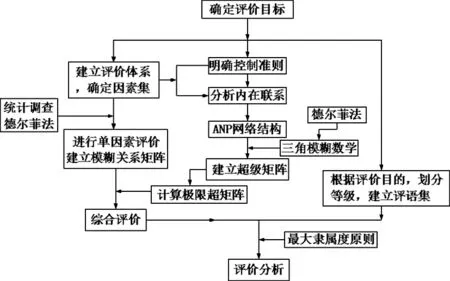
图2 F-ANP法计算步骤

2 F-ANP网络模型的构建

2.1 构建未加权的二级指标超级矩阵

根据1.1节描述的网络结构，将管理水平指标体系分为5个元素集，每个元素集又分为若干个元素，各元素之间存在相互依存的关系，且元素集内部元素也存在相互影响的关系，征询专家的意见后，采用三角模糊数表示。因篇幅有限，仅显示计算结果，构建的二级指标未加权超级矩阵W如图3。

图3 构建的二级指标未加权超级矩阵W

2.2 构建一级指标模糊权重

对于一级指标的权重，采用AHP法。关键在于构建判断矩阵。由于一级指标内容与现有管理评价标准类同，因此在确定指标间的重要性时，主要根据分值分布情况，对于分值高的指标，则重要性更大，反之亦然，最终得到元素集的权重矩阵A：

将求得的二级指标超级矩阵与一级指标权重矩阵相乘，则可构建模糊加权超矩阵：

2.3 计算极限超矩阵

将W代入式（2），通过不断矩阵迭代相乘及归一，求得极限超级矩阵。最终，获得归一化特征向量为：

对特征向量各元素大小进行排序，排序结果为：档案管理<注册鉴定<工程划界<信息化水平<管理设施<管理手册<安全生产<库区管理<应急管理<工程形象<考评激励<工程观测<运行操作<设备保养<管护经费<机构人员<调度运用<工程检查<维修养护<责任人<防汛度汛。从排序结果可知，水库的防汛安全应作为水库管理最重要的工作。

3 实例应用

3.1 模糊关系矩阵

根据以上建立的F-ANP网络模型，选取江西省某两座水库（分别为水库1、水库2）作为应用实例。现选取熟悉水库管理的5名专家组成评审团，以问卷调查的形式对第2层元素进行单因素评价，构造模糊评判矩阵R，有关数据见表2。

表2 模糊评判矩阵数据

3.2 综合评价

计算结果为 B1=（0.088，0.262，0.336，0.246，0.068），B2=（0.018，0.082，0.286，0.346，0.268）。根据最大隶属度原则，最大权重值对应的评价集作为水库的管理评价等级，水库1各评价集最大权重为0.336，隶属评价集为三级，表明水库1的管理等级为三级；同理，水库2最大权重值为0.346，隶属评价集为二级，表明水库2的管理等级为二级，管理水平比水库1要好。

为定量评价水库管理水平，不妨假定V=｛不合格、四级、三级、二级、一级｝各评价等级对应的分值为F=｛1分，2分，3分，4分，5分｝，其中，评价集等级越低，水库得分越高。将F代入式（4）

式中：F为评价集分值向量，H可表示水库综合得分。经计算，H1=2.944分，H2=3.764分，水库2管理水平优于水库1，与最大隶属度原则求得的结果相符合。

4 结论

科学合理的管理评价方法是实现精准施策、提高水库管理水平的主要手段。目前应用模糊综合评价时，指标权重的确定是主要难点之一。为此，本文采用网络结构法，通过引入三角模糊数法，分析水库管理指标的内在联系，建立管理指标网络模型。利用超级矩阵及极限矩阵，分析了各指标权重大小。以两座水库为计算案例，开展了水库管理模糊综合评估。研究结果表明，FANP法的计算结果较为客观和稳定，方法具有普遍性及通用性，在水库综合管理评价中具有应用价值。