基于累加性和均衡性的林分质量综合评价方法*

张岗岗 惠刚盈

(1.中国林业科学研究院林业研究所 国家林业和草原局林木培育重点实验室 北京 100091；2.河南师范大学 新乡 453007)

森林质量是森林在生态、社会和经济效益方面的所有功能与价值总和(Dudleyetal., 2006)，及时进行森林质量评价，反映森林资源质量现状和变化趋势，可为政府和企业制定森林资源可持续经营战略、提高森林资源管理水平和改善区域生态环境提供科学依据(曲松，2008)。近年来，众多学者根据不同研究目的对森林质量评价开展了大量研究(赵惠勋等，2000；党普兴等，2008；曲松，2008；王乃江等，2010；邓海燕等，2017；安慧君等，2018)，但评价方法各异(安慧君等，2018)，尚无统一的评价指标体系(邓海燕等，2017)，评价结果的可靠性难以令人信服(安慧君等，2018)。林分状态是林分在自然生境中所处的状况和特征(惠刚盈等，2016a)，既是林分动态变化过程中测度时点林分质量的具体表达，也是森林未来生长潜力和发展方向的基石，基于林分状态的森林质量评价时效性和可操作性较强，其评价结果对森林经营措施调整具有重要启示作用，是有效提升林分质量的必要手段。林分质量综合评价是森林经营决策的前提和关键，只有构建科学的指标体系、选择合理的评价方法评估现实林分质量优劣，才能有针对性地制定森林经营措施，精准提升林分质量。

综合评价是指对以多属性体系结构描述的对象系统作出全局性、整体性评价，既要考虑各评价指标的“累加性”(各评价指标值大小)，又要兼顾各评价指标之间的“均衡性”(强调各评价指标值之间的协调性)(郭亚军等，2001；漆艳茹，2010)。当前，不同综合评价方法及其应用广泛深入开展(Mendozaetal.，2005；Ochoa-Gaonaetal.，2010；Stafoggiaetal.，2011；Thomasetal.，2014；Thiviergeetal.，2014；张会儒等，2014；Lietal.，2015；Franketal.，2015；王得祥等，2015；惠刚盈等，2016a；Valls-Donderisetal.，2017)，但大多数研究偏重强调不同评价对象最终评价得分，并未考虑不同指标之间的均衡性。如王乃江等(2010)采用层次分析法评价黄土高原蔡家川林场森林质量，仅考虑了森林质量累加性，且评价结果两两相等的样地高达38.8%，无法判别和排列评价值相等的林分质量优劣。根据木桶原理(短板理论)和利比希最小因子定律(Hooker，1917)可知，评价对象优劣取决于最小值，如某些评价对象的指标取值分别为(1，3，5)和(3，3，3)，虽然其总评分相等，但前者取值为1的因子可能成为评价对象优劣的限制因素(Yangetal.，2018)。因此，科学的林分质量评价模型应既能准确刻画林分质量各方面功能大小，又能客观反映其指标之间的协调性，完整的评价体系本质上是系统累加性和均衡性的协调统一(Zhangetal.，2018)，以全面评估林分整体质量并有效促进其均衡发展。此外，雷达图法(Saary，2008；Stafoggiaetal.，2011)和单位圆法(惠刚盈等，2016a；李录林等，2018)依据指标多少等分圆周，忽略了各指标之间的相对重要程度，而权重代表生态系统中各生态要素的重要性和地位，其大小既反映该指标体现生态指标总目标的程度或比例，又直接影响生态指标体系的评价结果和使用效果(吝涛等，2007；漆艳茹，2010)，因此，综合评价中考虑权重也尤为重要。

鉴于此，本研究以甘肃小陇山林区锐齿栎(Quercusalienavar.acuteserrata)天然林、吉林蛟河林区阔叶红松(Pinuskoraiensis)混交林和模拟天然林为例，基于等周定理和等圆理论试图提出林分质量均衡性测度指标，并构建兼顾林分质量累加性和均衡性的综合评价模型比较不同林分质量优劣，以期为林分质量问题诊断及精准提升提供参考。

1 材料与方法

1.1 试验林分

锐齿栎天然林(a和b)位于甘肃省小陇山林区百花林场小阳沟(33°30′—34°49′N，104°22′—106°43′E)，该区属暖温带湿润-中温带半湿润大陆性季风季候，海拔1 000～2 000 m，年均气温7～12 ℃，年均降水量600～900 mm，以山地棕色土和褐土为主，地处我国华中、华北、喜马拉雅和蒙新四大自然植被区系交汇区，海拔2 200 m以下是以锐齿栎和辽东栎(Quercusliaotungensis)为主的天然林。阔叶红松林(c和d)位于吉林省蛟河林业局东大坡经营区(45°51′—44°05′N，127°35′—127°51′E)，该区属温带大陆性季风山地气候，海拔在800 m以下，年均气温3.5 ℃，年均降水量700～800 mm，以暗棕壤为主，地处长白植被区系，主要有红松阔叶混交林和硬阔叶林等天然林。林分e和f为模拟天然林。样地概况见表1。

表1 样地概况

1.2 研究方法

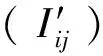
1.2.2 指标赋权 采用熵权法(Guey-Shinetal.，2011；Gorgijetal.，2017)对各指标赋权，得到第i个林分各指标的权重向量p=(pi1,pi2,…,pin)。

1.2.3 图形绘制 将单位圆划分成n个圆心角分别为θij=2πpij的扇形区域，每个扇形半径和圆心角分别代表单个指标取值和权重大小，整体上形成反映林分质量的闭合图形。

1.2.4 特征向量提取 设sij、lij分别表示第i个林分闭合图形中第j个指标所对应扇形的面积和弧长，则第i个林分闭合图形的面积Si和弧长Li特征量分别为：

(1)

(2)

式中：Iij和pij分别为第i个林分第j个指标取值和权重大小；n为指标个数。

当所有指标均取1时，林分质量最优，此时林分对应闭合图形的面积和弧长最大，且分别恒等于单位圆面积Smax=π和圆的周长Lmax=2π，此即最优林分质量期望值。

1.2.5 评价向量构造 设ωi1、ωi2分别表示第i个林分的累加性和均衡性，则第i个林分的评价向量ωi=(ωi1，ωi2)。

1)林分累加性(ωi1)定义为林分质量各评价指标累加值大小，采用第i个林分对应闭合图形面积Si与最优林分质量期望值Smax的相对大小表示，其计算式为：

ωi1=Si/Smax=Si/π。

(3)

式中：ωi1∈[0，1]，其值越大，林分质量累加性越强。

2)林分均衡性(ωi2)反映林分不同评价指标之间的协调性，采用αi2、βi2和γi23个指标测度。

①基于单位圆的αi2和βi2指标 由等周定理可知，面积相等的几何图形中圆的周长最小，周长相等的几何图形中圆的面积最大(Osserman，1978；Kesavan，2002)，若某一几何图形的周长与其等面积的圆的周长越接近或某一几何图形的面积与其等周长的圆的面积越接近，则该几何图形越趋于圆形。因此，可用单位圆中第i个林分闭合图形的弧长与其等面积的圆的周长的比值(αi2)或该几何图形的面积与其等周长的圆的面积的比值(βi2)(Zhangetal.，2018)表达单位圆中各指标接近圆边缘的程度，即以圆的边缘为参考，测度各指标之间的接近程度，借此表达各指标之间的均衡性：

(4)

βi2=π(Li/2π)2/Si。

(5)

式中：αi2、βi2为第i个林分质量的均衡性，介于[0，1]，二者均可反映林分质量各评价指标之间的协调发展程度，其值越大，林分质量各方面越均衡。

②基于等圆的γi2指标 众所周知，半径(Rci)、面积(Sci)或周长(Lci)相等的圆为同圆或等圆，由Sci、Lci数学推导可得：

Rci=2Sci/Lci。

(6)

在同圆或等圆中，所有半径均相等，当已知几何图形的面积、周长时，可求得与此面积和周长对应的圆的半径Rci，该圆的所有半径均相等。因此，可采用不同林分质量各评价指标平均值与此圆半径的差异程度衡量不同评价指标之间的协调性，即：

(7)

(8)

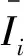
1.2.6 评价函数构造 采用ωi1和ωi2的几何均值构造评价函数Fi，即：

(9)

式中：Fi为第i个林分质量的综合评价值，Fi∈[0，1]，其值越大，林分质量越优良；反之越差。

1.3 数据处理与分析

以锐齿栎天然林(a和b)、阔叶红松林(c和d)和模拟天然林(e和f)的林分质量综合评价为例，从林分结构和活力2方面筛选出10个评价指标(惠刚盈等，2016a)，采用赋值法和熵权法分别对各指标进行标准化和赋权，利用Excel 2016、Origin 2017和Adobe Illustrator CC 2018软件进行数据计算和作图，分别以各指标等权重和不等权重2种情况比较不同天然林林分质量优劣。林分质量评价指标体系和计算公式详见文献(惠刚盈等，2016a)，等权重下林分c和e以及不等权重下林分d和f累加性分别相等，以此验证现有βi2和本研究提出的αi2和γi2测度各指标均衡程度的有效性。

2 结果与分析

2.1 不同天然林林分质量特征

锐齿栎天然林(a和b)为复层林，直径分布呈倒J形，符合典型异龄林直径分布特征，林分中苗高>50 cm的更新幼苗数量分别达8 100和7 480株·hm-2，更新良好，但二者均较为拥挤(表2)；林分a呈随机分布，混交较好，整体长势优良且目的树种优势明显，健康林木比例较高，而林分b为多优势树种混交林，林木水平分布格局为均匀分布，混交状况、林分长势和顶级种竞争势相对较差，健康林木比例相对较低。阔叶红松林均为随机分布，直径分布呈倒J形，健康林木比例≥90%，但较为拥挤且更新一般；林分c为多层混交林，混交度相对较低，顶级种竞争势不明显，而林分d为多优势树种复层混交林，混交状况和目的树种优势较高。林分e和f均为不完整异龄复层林，健康林木比例>90%，林分长势、密度、更新和顶级种竞争势处于中等水平，其中，林分e树种丰富且林木随机分布，而林分f为团状分布，树种组成简单且多样性相对较低。

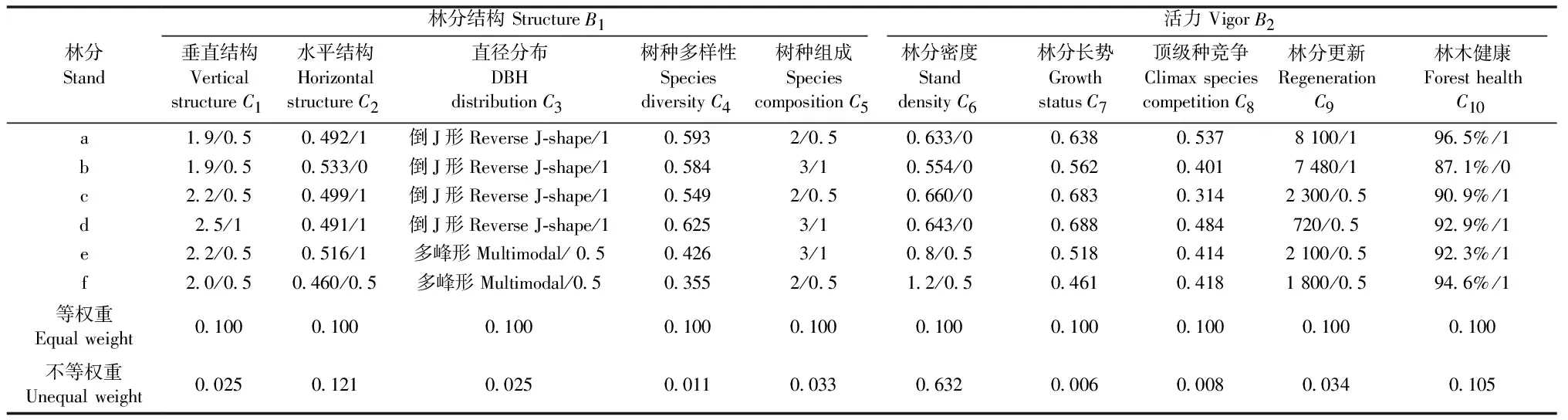
表2 天然林林分质量各指标取值

2.2 等权重下不同林分质量综合评价特征值

等权重下阔叶红松林c和模拟天然林e闭合图形面积相等(图1)，ωi1均为0.462，表明二者累加性相等。林分e中C2、C5和C10取值均为1，即绝大多数为健康林木且为多优势树种组成的随机分布林分，其他方面各指标取值相对集中，而林分c中C2、C3和C10取值均为1，即该林分直径分布呈倒J形，90%以上为健康林木且林分整体呈随机分布，其他方面离散程度较大，其αi2、βi2和γi2均小于林分e。这说明，不同林分累加性相等时，可借助αi2、βi2和γi2比较各林分质量评价指标的均衡性，且3个指标评价结果一致。

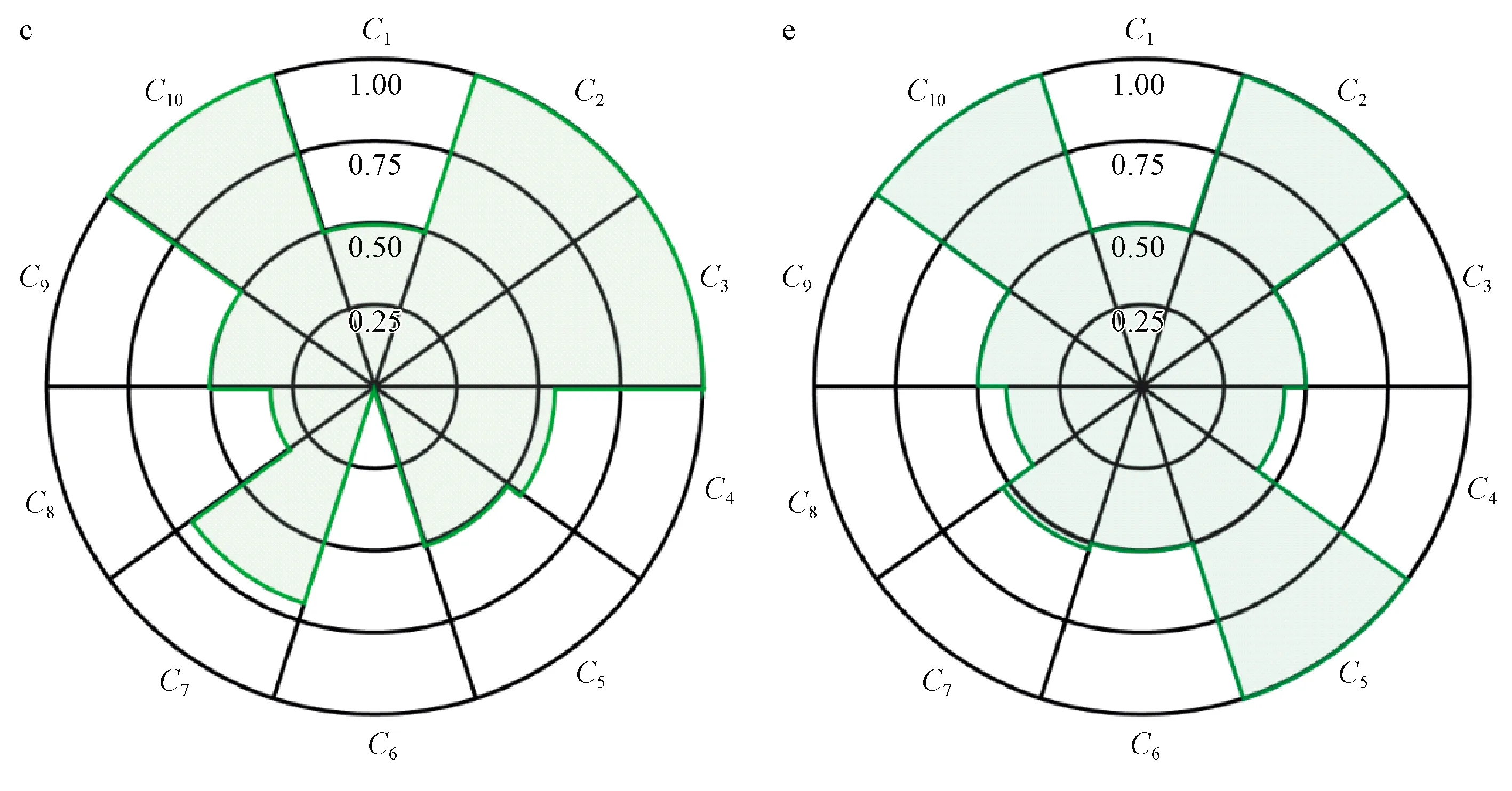
图1 等权重下不同天然林(c和e)单位圆示例

等权重下锐齿栎天然林(a和b)和阔叶红松林(c和d)ωi1分别为0.555、0.407、0.462和0.635(表3)，不同林分累加性由大到小排序为d>a>c>b，即林分d累加性较为优良，林分a和c次之，林分b相对较差。不同天然林αi2、βi2和γi2均表现为d>a>c>b，即林分d各指标取值差异较小，林分质量各方面发展相对均衡，林分b各指标离散程度较高，仅个别方面较为优良。虽然不同天然林αi2、βi2和γi2各指标取值大小不同，但其均衡性判别结果一致，侧面反映出这3个指标测度林分质量均衡性的有效性。结合ωi1和ωi2可知，不同天然林综合评价值排序为d>a>c>b，阔叶红松林d林分质量最为优良，林分a次之，然后为林分c，锐齿栎天然林b质量最差。

表3 等权重下不同天然林质量特征值

2.3 不等权重下不同林分质量综合评价特征值

不等权重下阔叶红松林d和模拟天然林f闭合图形面积相等(图2)，ωi1均为0.327，表明二者累加性相等。林分d中C6圆心角最大，但取值为0，C1～C3、C5和C10取值均为1，圆心角相对较大，其余扇形半径和圆心角均较小，即其余指标取值和权重均较小，而林分f各指标权重与林分d相同，该林分中90%以上为健康林木(C10=1)，其余指标离散程度较小，αi2、βi2和γi2分别为0.963、0.926和0.930，均显著大于林分d，即林分f的均衡性明显优于林分d。这说明，不同林分累加性相等时，αi2、βi2和γi2可有效比较林分质量各评价指标的均衡性，且评价结果具有一致性。

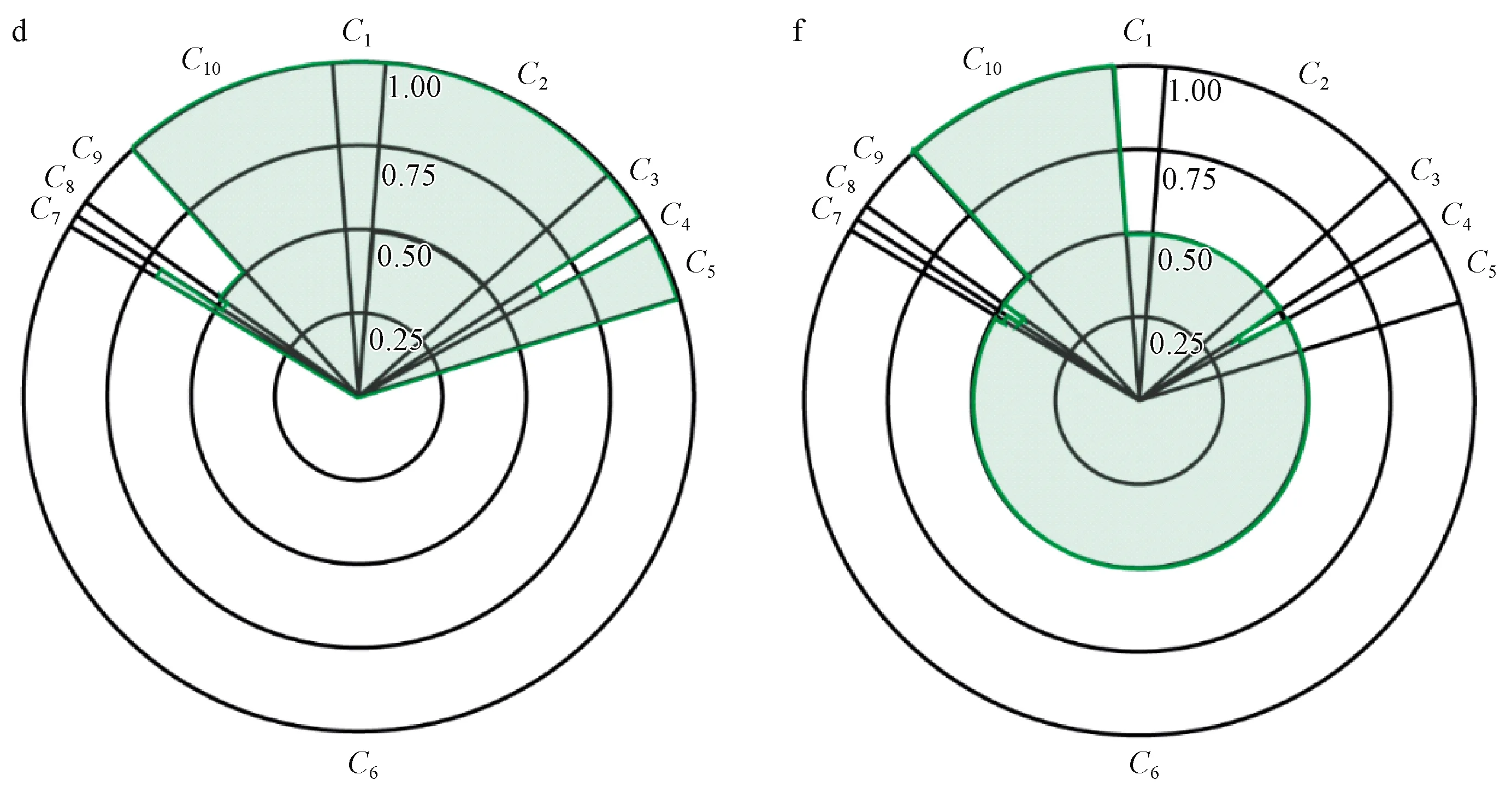
图2 不等权重下不同天然林(d和f)单位圆示例

不等权重下锐齿栎天然林(a和b)和阔叶红松林(c和d)ωi1分别为0.308、0.105、0.281和0.327(表4)，即林分d累加性最优，林分a和c次之，林分b相对较差。不同天然林αi2、βi2和γi2大小存在差异，但其均衡性判别结果一致，均表现为d>a>c>b，即林分d林分质量各方面发展最均衡，林分b各指标离散程度较高，仅个别方面较为优良，反映出这3个指标测度林分质量均衡性的有效性。不同天然林综合评价值排序为d>a>c>b，即阔叶红松林d林分质量最为优良，林分a次之，然后为林分c，锐齿栎天然林b质量最差。

表4 不等权重下不同天然林质量特征值

3 讨论

本研究提出的新方法兼顾林分质量累加性和均衡性，优于以往侧重累加性的评价方法，雷达图(Saary，2008；Stafoggiaetal.，2011；Lietal.，2015；Franketal.，2015)、目标图(Stafoggiaetal.，2011)、Spie图(Stafoggiaetal.，2011；Thomasetal.，2014)、单位圆法(惠刚盈等，2016a；李录林等，2018)、综合指数法(Jiangetal.，2015；Wiréhnetal.，2015)、层次分析法(王乃江等，2010；张会儒等，2014；王得祥等，2015；Coulteretal., 2015)等强调各评价对象的累加性优劣，适用于评价对象累加性定量或定性分析。根据木桶原理(短板理论)和利比希最小因子定律可知，最小因子决定评价对象整体优劣(Hooker，1917)，因此，在考虑评价对象累加性的基础上，各评价指标之间应有相应的均衡性，否则评价结果可能会出现“表面上的科学性掩盖着实质上的不科学性”的现象(郭亚军等，2001)。科学的评价模型应既能准确刻画评价对象各方面功能大小，又能客观反映各指标之间的协调性，完整的评价体系本质上是系统累加性和均衡性的协调统一(Zhangetal.，2018)。累加性相等的林分c和e及d和f比较结果表明，现有βi2(Zhangetal.，2018)与本研究提出的αi2和γi2均能较好表达不同林分质量各指标之间的协调程度，且三者之间具有较强一致性，是对综合判别林分质量优劣方法的有效补充和完善。在累加性评价基础上引入均衡性测度的优越性在于，若采用如上所述单位圆法、综合指数法、层次分析法等测度若干评价对象累加性出现评价结果相等或相近时，可借助αi2、βi2和γi2均衡性测度方法进行比较，以确保综合评价结果的可靠性、全面性和客观性。因此，本研究提出的综合评价方法兼顾了林分质量累加性和均衡性2方面，可全面评估林分整体质量，并有效促进其均衡发展。

本研究提出的改进单位圆与单位圆(惠刚盈等，2016a)均借助单位圆中闭合图形面积累加值评判不同评价对象累加性的优劣，二者累加性排序结果完全一致，均表现为d>a>c>b。单位圆首先需要依据指标值大小进行排序，并根据形成的闭合图形中扇形和三角形面积累加值测度累加性大小(惠刚盈等，2016a)，适用于等权重评价对象的定量评价，而改进单位圆采用每个扇形半径和圆心角代表单个指标取值和权重大小，运用各扇形面积累加值测度林分质量累加性，并根据αi2、βi2和γi2得出不同天然林均衡性为d>a>c>b，综合评价排序也为d>a>c>b。因此，改进单位圆兼顾了指标权重和均衡性，更具普适性和说服力。

改进单位圆具有评价指标体系的完备性。完整评价指标体系的数学描述为Z=f(E，S，W)，其中，Z表示评价指标体系；E表示评价指标体系所有构成要素(指标)的集合；S表示按照一定规则构成的层次结构，反映指标间的所属及其相互关系；W表示指标的权重集合，反映单一指标对整个研究对象影响重要程度的量化；f表示E、S、W之间相互联系、相互作用的函数关系(杜锁房，2006)。改进单位圆全面呈现了评价指标体系的三要素，即借助改进单位圆中若干扇形半径和圆心角分别表征指标集合和权重，基于指标层C的顺序排列间接反映评价指标体系的层次结构，基于扇形面积和弧长的计算反映不同元素之间的函数关系，可直观体现出指标体系的构成要素和层次结构，并有效表达出各指标的相对重要程度，具有较强的综合性和普适性，而雷达图法(Stafoggiaetal.，2011；Lietal.，2015；Franketal.，2015；Thomasetal.，2014)和单位圆法(惠刚盈等，2016a；Zhangetal.，2018)仅反映指标体系要素集合，无法全面呈现指标体系的完备性。

基于累加性和均衡性的林分质量综合评价方法更为全面客观，其评价结果对林分质量问题诊断和森林经营决策具有重要启示作用。单位圆中的1.00、0.50、0.25同心圆分别是最优、平均和较差林分质量的基准线，大于0.50被认为是合理指标(惠刚盈等，2016b)。因此，在现实森林经营实践中，需根据不同林分质量不合理指标分布状况，优先制定经营措施解决这些问题，即经营措施优先性(惠刚盈等，2016b)，同时保证林分全面均衡发展。如林分a累加性相对较好，但较为拥挤，可能成为林分健康稳定的短板，需要抚育采伐或打枝(Bauhusetal.，2015)；林分b累加性和均衡性最差，需要多措并举，包括单株择伐(Nyland，1998)不健康林木，优先调整顶级种竞争微环境、水平分布格局和密度，同时提升林分均衡性，确保林分全面均衡发展；林分c与d均需要优先调整林分密度和顶级种竞争微环境，但林分c在垂直结构、树种多样性和组成及其均衡性方面不如林分d，经营迫切性(惠刚盈等，2010)更为紧迫，应尽早改善林分质量。兼顾林分质量累加性和均衡性的经营措施优先性和森林经营处方(惠刚盈等，2016b)有助于全面提升林分质量，并有效促进林分均衡发展。

4 结论

锐齿栎天然林和阔叶红松林累加性、均衡性和综合评价值均表现为d>a>c>b，即阔叶红松林d累加性最好，林分各方面发展较为均衡，整体质量最优，其次是林分a和c，锐齿栎天然林b质量较差。累加性相等的林分c和e及d和f比较结果表明，现有βi2以及本研究提出的αi2和γi2均能有效测度林分质量各评价指标间的均衡性，且评价结果具有较强一致性，ωi1可量化描述林分质量累加性优劣，Fi能全面刻画林分质量综合评价结果，林分质量单个或多个方面的改善可有效提升林分整体质量并促进其均衡发展。