盾构下穿地下综合管廊变形规律的数值模拟研究

文｜中天建设集团有限公司 金明亮/中天建设集团有限公司，长安大学 李浩然/长安大学 李明倩

1 引言

地下综合管廊解决了“拉链式路面”的弊病，成为建设“海绵城市”的重要载体。盾构施工会不可避免地对地下结构周边土体产生较大扰动并触发相关建筑物应力重分布。揭示盾构施工对地下综合管廊变形的影响机理成为地下工程建设需要解决的重要问题之一。对盾构施工引起既有地下结构的变形破坏，部分学者开展了数值模拟研究。例如，杨广武等采用Flac3d软件对盾构下穿隧道施工进行数值模拟，分析了地铁隧道沉降的变化规律，得到了地基变形模量和沉降量的关系。胡军等针对盾构下穿既有地铁暗挖隧道进行数值模拟，得到了隧道横向扭转随盾构推力的变化规律。祝树红等利用ABAQUS 软件，研究了盾构下穿过程中的土体扰动和邻近既有管线的变形规律。张文超等利用ABAQUS 软件对盾构下穿隧道施工进行数值模拟，分析了不同覆土厚度和隧道间距对隧道应力和位移的影响。张平采用ANSYS 软件模拟盾构下穿既有管线，计算了管线和邻近土体的相互作用力以及隧道开挖时地下管线变形量。Li 等建立了不同工况下盾构下穿隧道的有限元模型，对隧道各节段的应力和变形进行了分析。Li 等分别采用经验公式模型、等效地损模型和随机介质理论模型计算了盾构下穿隧道施工引起的沉降，分析了各模型主要参数对计算结果的影响。史晓涛构建了盾构近距离下穿隧道的数值分析模型，研究了不同断面和工况下的盾构隧道施工位移场变化规律。方继安等采用Flac3d软件分析了盾构隧道开挖速度、掌子面支撑压力比、隧道直径和管隧间距等因素对既有管线沉降的影响。

Flac3d作为材料三维结构受力特性模拟和塑性流动分析的经典软件，越来越多地用于地下结构施工模拟中，本文采用该软件对盾构下穿地下综合管廊施工进行模拟，分析地下综合管廊的沉降和各管节的变形规律。

2 实验设计

2.1 实验模型

建立了盾构隧道-土体-管廊的三维有限差分模型，该模型长75m、宽45m、高40m。管廊上顶板埋深3m、底板埋深6m，盾构隧道顶部埋深12m、直径6m，管廊断面采用3m×3m，结构顶板及侧板厚0.3m，底板厚0.35m，每15m 设置一条变形缝，如图1所示。

2.2 模型参数

模型中土体采用砂土，本构关系采用摩尔库伦模型，土体参数如表1所示。

管廊结构（管廊衬砌、注浆材料、盾壳、管片）均采用线弹性力学本构关系，材料参数如表2所示。

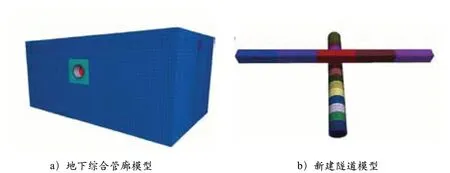
图1 盾构隧道-土体-管廊结构三维模型

表1 土体参数

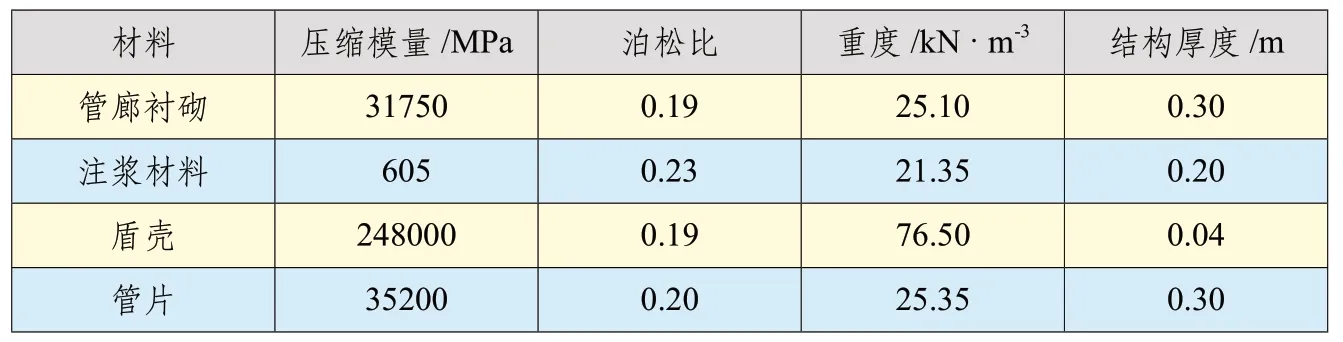
表2 管廊结构材料参数

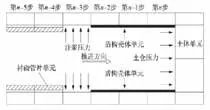
图2 刚度迁移法示意图

3 计算模拟过程

盾构施工开挖的前进支护过程如图2所示。在盾构机沿设计隧道中心线开挖时，以3m 为一个开挖步，共开挖15 步，总开挖距离45m。

本模型中盾构采用欠压方式推进，掌子面土压力为梯形荷载，其大小按欠压比为0.4 进行施加。欠压比如式1 所示。

式中：p 和p0 分别表示掌子面施加压力和理论压力。在该模型中建立接触面，如图3所示。

4 管廊沉降监测结果分析

4.1 监测点设置

在管廊结构上设置沉降监测点，由于管节1～管节5 关于管节3 的中线对称，因此本文仅列出管节1～管节3 结构的沉降监测点位置和编号，如图4所示。

管廊结构共布置3 个测面35 个监测点，采用双段法对各监测点命名，例如，3-1 点表示第三侧面从左到右数第一个监测点。

4.2 监测点沉降分析

将管节2～管节4 沉降监测点数据绘制成曲线，如图5所示。

由图5可知：

（1）各监测点均经历了沉降缓慢及加剧阶段（-19.5m～-4.5m）、沉降剧烈阶段（-4.5m～4.5m）、沉降趋缓及稳定阶段（4.5m以上）。

图3 接触面模型

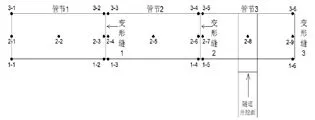
图4 管廊沉降监测点

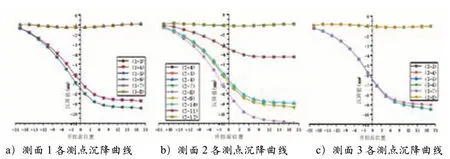
图5 各测点沉降曲线（横坐标以开挖面位于管廊中心为零点，未到达中心为负，超过中心为正）

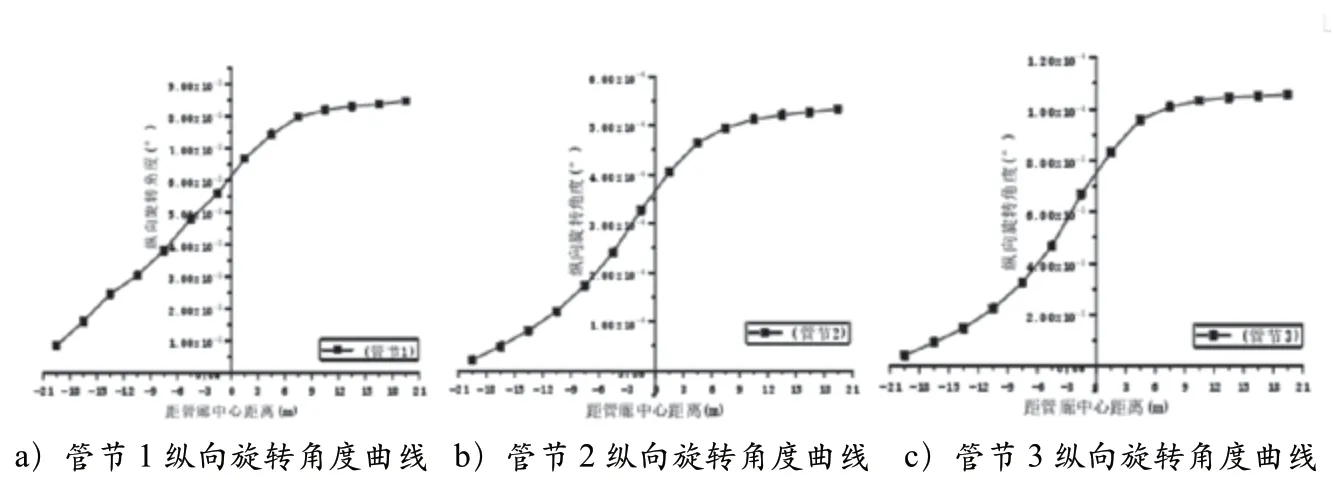
图6 管节旋转角度曲线图

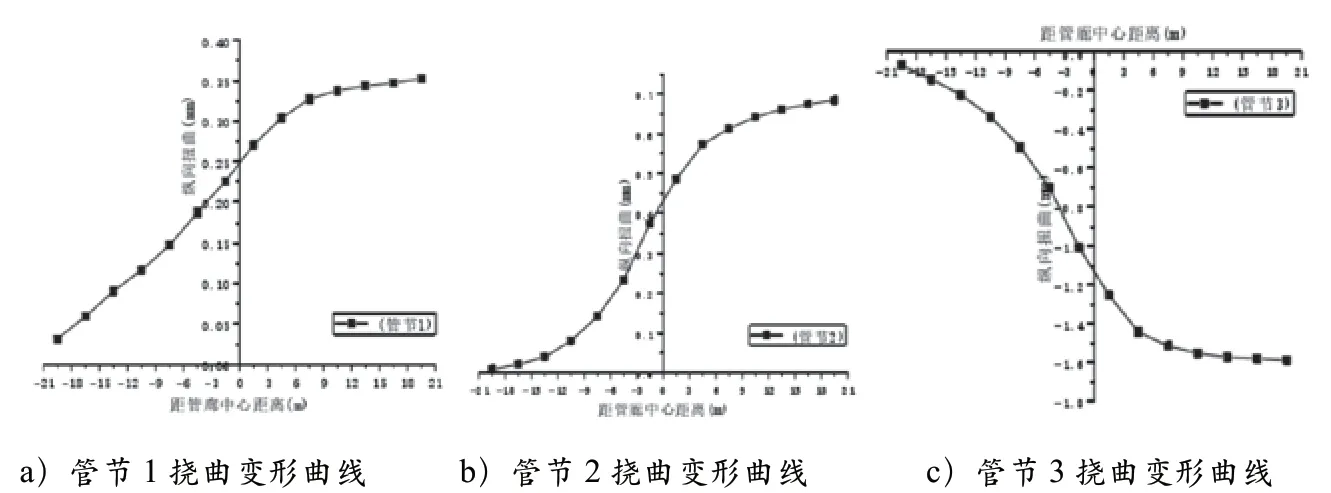
图7 管节挠曲变形曲线

（2）不同测面、不同阶段的沉降值不相同：

距盾构隧道中心越远，管廊结构沉降值越小；

管廊结构在盾构下穿过程中产生了横向倾斜或扭转；

沉降监测点1-3、2-4、3-3 后期均产生了一定程度的上升，说明该管节产生了旋转。

4.3 管节变形规律分析

（1）纵向旋转分析

管节的纵向旋转通过第二测面沉降值表示，如式2 所示。

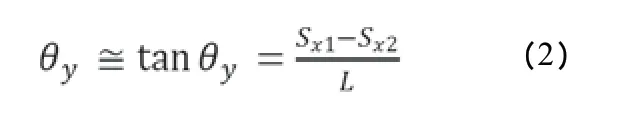
式中：Sx1、Sx2为监测点沉降值，y、L为单管节编号和长度。分别绘制管节1～管节3 的纵向旋转角度曲线，如图6所示。

由图6可知：

随着盾构开挖面的推进，管节的旋转角度逐渐增大；

盾构接近并通过管廊中线之前对管廊结构的旋转影响大于盾构通过并远离管廊时的影响；

盾构施工对距隧道中线较远的管节1影响较小，对较近的管节2 影响大。

（2）纵向挠曲分析

管节的纵向挠曲通过第二测面沉降值表示，如式3 所示。

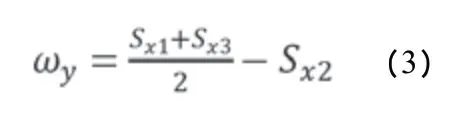
式中：Sx1、Sx2、Sx3分别表示管节1～管节3 第二测面监测点的沉降值。分别绘制管节1～管节3 的挠曲变形曲线（规定向上为正、向下为负），如图7所示。

由图7可知：

管节1、2 纵向挠曲为正，说明其发生“凸” 形变形，管节3 纵向挠曲为负，说明其发生“凹”形变形。比较管节纵向挠曲的绝对值，说明距中心线越近挠曲变形越大；管节组合产生了“柔性”的纵向挠曲变形。

（3）相对扭转分析

三个测面的监测点沉降值不相等，说明管廊结构产生了相对扭转，如式4 所示。

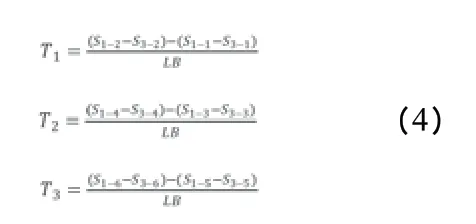
式中：T1、T2、T3为管节1～管节3的相对扭转，其他符号意义不变。分别绘制管节1 和管节2 的相对扭转曲线，如图8所示。

由图8可知：

管节1、2 的相对扭转曲线变化趋势类似；随着盾构施工进行，盾构开挖面逐渐靠近管廊中心，管节的相对扭转逐渐增大，当盾构开挖面距管廊中心-4.5m 左右时，管节相对扭转达到最大值，此时管节1 相对扭转为1.84×10-6rad/m，管节2 相对扭转为5.92×10-6rad/m，说明距盾构隧道中线越近的管节相对扭转越大；

（4）差异沉降分析

将管节2 和管节3 间前端面和后端面的差异沉降绘制成曲线，如图9所示。

由图9可知：

盾构开挖面接近管廊前端面过程中产生的差异沉降大于盾构开挖面通过管廊中心之后产生的差异沉降。

5 结论

本文利用Flac3d软件对盾构下穿地下综合管廊的变形规律进行数值模拟分析，得到以下结论：

（1）管廊单管节的变形主要为纵向旋转、纵向挠曲和横截面的相对扭转，多管节组合变形则呈现“柔性”的特征。

（2）在盾构开挖面穿过管廊前后端面阶段最容易发生事故。

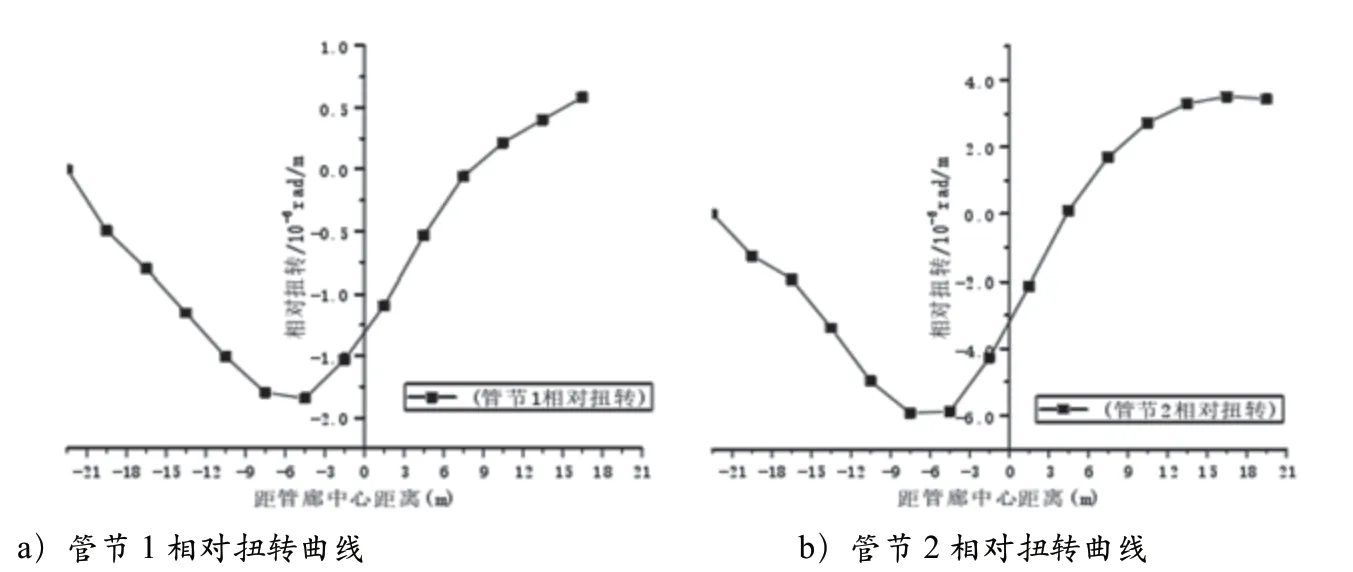
图8 管节相对扭转曲线

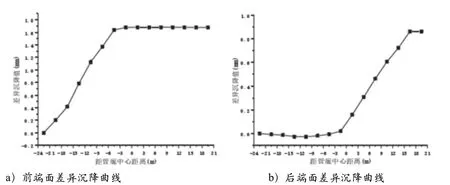
图9 差异沉降曲线