BP神经网络模型在深基坑爆破振速上的应用研究
张 齐,贾文超,莫爵同
(广东省工程勘察院 广州510510)
0 前言
深基坑爆破工程普遍存在危险程度高、爆破振动影响范围广等特点,近年国内外爆破工程事故频繁发生,引起了相关单位的高度重视。而为了提高爆破效率,应掌握爆破安全可控度,减小深基坑爆破施工对周边环境的影响[1-3]。在深基坑用药量较小的试爆阶段,需要积累数据并对振速进行预测,在后续工作中指导信息化施工。
城区内深基坑爆破工程周边环境含有大量振动敏感建筑,如广州地铁某项目基坑爆破影响范围内存在既有地铁三号线、重要医院、区政府大楼及周边的各种敏感管线等,在这些环境振动敏感地区进行深基坑爆破施工作业,振速监测单位需要提前预测爆破振动强度,减小爆破对周边环境的影响,爆破振速的预测,对周边环境安全及后续基坑开挖方案的完善有着重要的指导意义。《爆破安全规程:GB 6722—2014》和国内外学者的诸多研究中常用萨道夫斯基经验公式进行爆破振速预测,周边建构筑物的爆破振动速度与诸多因素有关,如震心与测点的水平距离、震心与测点的高差、最大单段用药量、总用药量等,由于传统的萨道夫斯基经验公式考虑因素较少,其预测的振速与实际数据相比效果较差,相关研究表明其平均相对误差高达42%[4-7]。
在数据预测及处理时效性上,人工神经网络相较于其他方法优势明显,并且泛化能力强、容错性能好。本文以广州地铁某基坑爆破开挖影响周边建筑物的监测实例数据,构建BP 神经网络模型,并将其与萨道夫斯基经验公式预测的数值进行对比分析,探讨BP神经网络在深基坑爆破振速预测上的适用性。
1 BP神经网络原理与建模
1.1 BP神经网络原理
BP 神经网络一般由输入层、隐含层和输出层组成,隐含层可以是一层或多层,每个层中又包含许多单神经元,在BP 神经网络中,层与层之间的神经元是全连接,层内部的神经元之间是无连接的,其输入层和输出层激励函数可以根据应用的不同需要而异。BP 神经网络的主要训练过程可以分为2个部分:第一部分为正向传播过程,在给出的输入信息通过输入层经隐含层处理,并计算每个单元的实际输出值;第二部分为反向误差传播,若在输出层未能得到期望的输出值,则逐层递归地计算实际输出与期望输出之差值(即误差),以便根据此差值调节权值[[8-10]。BP神经网络模型结构如图1所示。
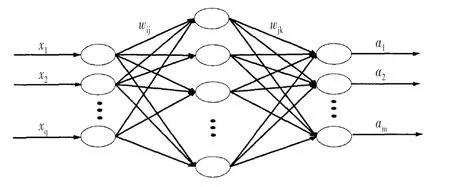
图1 BP神经网络模型结构示意Fig.1 Schematic of BP Neural Network Model Structure
1.2 BP神经网络建模步骤
1.2.1 输入的样本训练数据进行正向传播

1.2.2 输出误差反向传播
经过正向传播的计算,能够求出实际输出,然而一般情况下,实际的期望值与预测值之间存在误差,当两者误差超过了设定的允许值,这时开始对网络模型作相应的学习修正,该步骤如下:
⑴计算全局误差
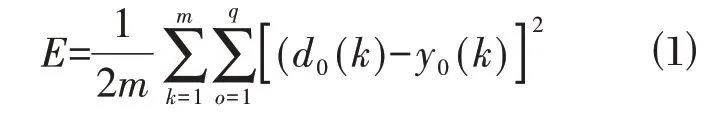
⑵计算误差函数对输出层的各神经元的偏导数δ0(k)[11]
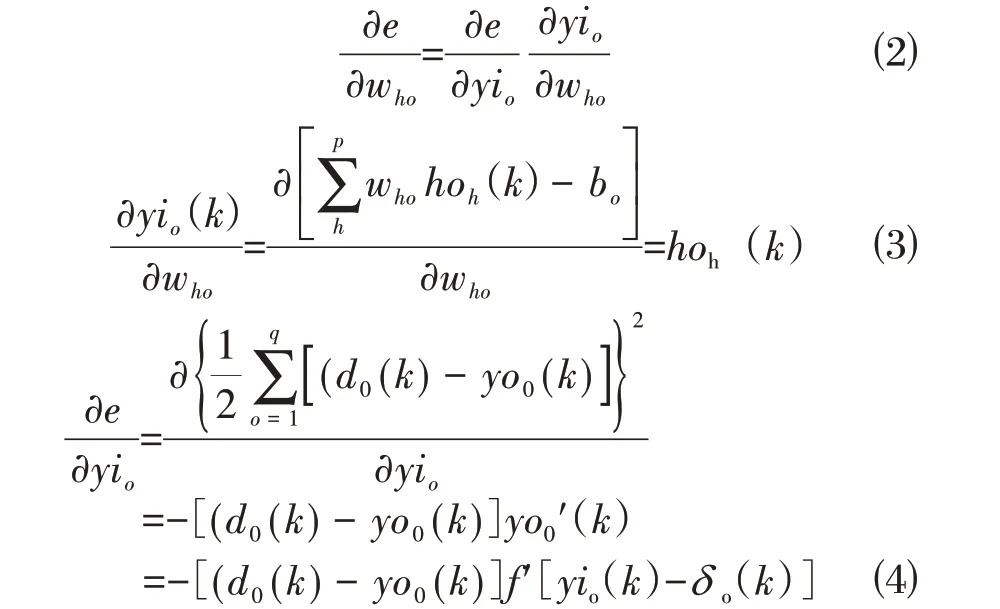
⑶利用隐含层与输出层的连接权值、输出层的δo(k)和隐含层的输出计算误差函数对隐含层各神经元的偏导数δh(k)[12]
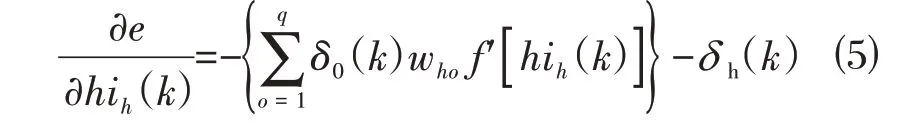
⑷ 利用输出层各神经元的δo(k)和隐含层各神经元的输出来修正连接权值who(k)。
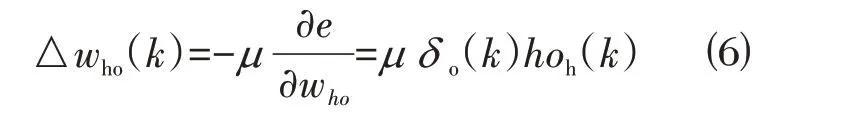
⑸利用隐含层各神经元的δh(k)和输入层各神经元的输入修正连接权wih(k)

1.2.3 样本循环训练及检查
要想提高BP 神经网络仿真模型的预测精度,输出误差满足设定要求,需要将BP 神经网络中输入的训练样本做循环记忆训练,每次完成循环记忆训练之后检查输出误差是否合限,若符合要求,可结束此学习过程,若不符合要求,则重复此过程[13-14]。
2 工程实例
2.1 工程概况
广州地铁10号线某项目基坑,西临中山一立交引桥、广州大道中路,北近在建地铁13号线,周边环境复杂,振动监测设备选用TC-4850 爆破振动记录仪,测点放置2 个水平传感器和1 个垂直传感器,传感器托盘采用石膏粉(石膏粉加少量水搅拌,5 min 后凝固)牢牢固定于预先筑好的平台上。振动测试点位如图2所示。

图2 振动测试点位Fig.2 Vibration Test Point
2.2 实验数据及实验环境
外业监测数据的采集及内业监测数据的处理采用中科测振的TC-4850设备及其配套的软件系统,BP神经网络及萨道夫斯基经验公式建模则采用Mat⁃lab2016a编写相应仿真程序进行预测分析。
本次实验采取前5 次试爆监测采取的23 组数据,监测数据如表1所示。
2.3 BP神经网络预测模型建立
2.3.1 输入层和输出层设计
BP 神经网络输入层神经元节点的数目,对于神经网络来说十分重要,节点数过少会造成预测精度不准确,而节点数过多则导致模型计算量过大,同时精度提升却不明显,所以需要根据实际应用的需要来确定。对深基坑爆破开挖影响建筑物振速监测的实际应用中,影响既有测点振速的因素很多,本文选取的主要影响因子有:测点与震心的高差(m)、测点与震心的水平距离(m)、最大单段用药量(kg)、总用药量(kg),包含测点振速(cm/s)的输入层的神经元节点数为5,输出层为测点振速(cm/s),神经元节点数量为1。具体设计如表2所示。

表2 输入及输出层设计Tab.2 Input and Output Layer Design
2.3.2 隐含层设计
根据以往建模经验,将隐含层节点数确定一个取值范围,在本工程实例训练样本数据的基础下,将所有取值范围内的节点数值逐个进行实验,根据实验结果取最小相对误差值对应的隐含层节点数,隐含层节点数取值范围的计算公式如式⑻:

式中:n为输入层神经元节点数量;q为输出层神经元节点数量;a 为1~10 之间的随机整数。通过式⑻结合输入层和输出层设计神经元节点数量,本次实验构建的BP神经网络结构隐含层神经元节点数量为3~13之间。
2.3.3 传递函数及学习函数的确定
传递函数对于网络的输出有着很大的影响,传递函数的特性将直接影响BP 神经网络的学习速率和仿真结果,本文根据实际需要采用sigmoid 函数为隐含层传递函数,输出层的神经元采用线性传递函数pure⁃lin函数。不同的学习函数采用不同的学习算法,在众多研究中LM 算法在同时兼具优秀的收敛特性下,极大地提高了BP 神经网络的收敛速度,是一种十分优秀的算法,本文学习算法采用LM算法。
2.3.4 模型参数的建立
本实验BP 神经网络仿真模型设定的参数如下:最大迭代次数为2 000,最小误差改进率为0.000 01,误差进度目标值为0.001,学习速率为0.05,最高失败次数为6。
2.4 数据预测及分析
利用训练好的BP 预测模型进行数据爆破振速预测,预测结果如表3所示。
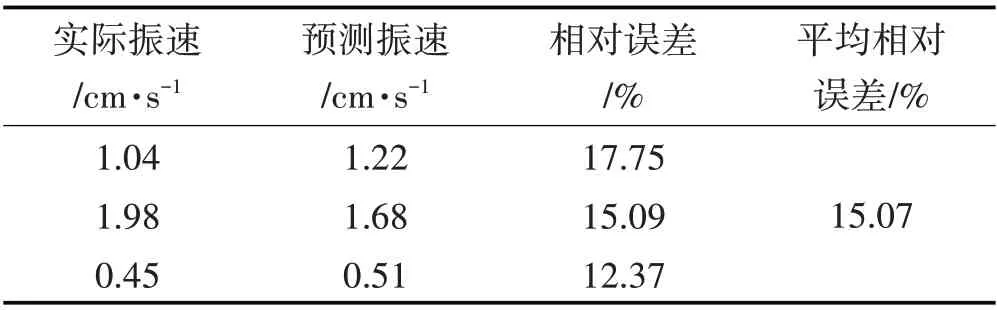
表3 BP神经网络模型下预测数据Tab.3 Forecast Data under BP Neural Network Model
国内普遍采用萨道夫斯基经验公式对爆破振速进行预测[15],其预测公式如下:

式中:V 为需监测对象的质点振速(cm/s);R 为需监测对象距离震心V 的爆心距(m);Q 为单段最大用药量(kg);k、a为与地质和地形有关的系数及衰减参数
式⑼中萨道夫斯基经验公式并不具备线性关系,要利用线性回归分析计算k、a 取值,其模型建立步骤如下:
⑴对式⑻两端取对数得到:

⑶利用最小二乘原理的线性回归分析计算k、a值。
利用萨道夫斯基经验公式预测结果如表4所示。
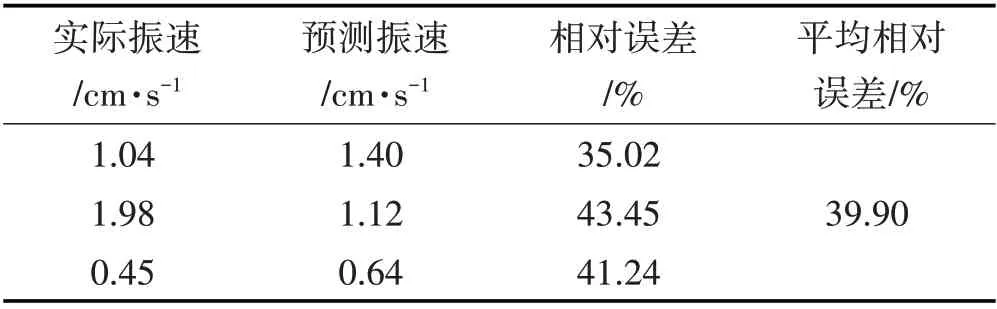
表4 萨道夫斯基经验公式下预测数据Tab.4 Predicting Data under Sadowski Empirical Formula
3 结论
本文介绍了BP 神经网络模型的原理及建模方法,并通过实例对BP 神经网络模型与传统的萨道夫斯基经验公式在振速预测上进行对比分析,结果表明:传统的萨道夫斯基经验公式在振速预测上精度较差,其最大误差为43.45%,平均相对误差为39.90%,而利用BP 神经网络模型对深基坑爆破振速进行预测,预测值达到了良好的精度效果,最大误差为17.75%,平均误差为15.07%。BP 神经网络模型相对于萨道夫斯基经验公式在振速预测上精度更高,可靠性更好,BP 神经网络模型在深基坑爆破振速监测领域内具有良好的适用性,可广泛应用。

