一种基于广义互相关的水声直扩信号检测方法
张 伟,董阳泽,张刚强,刘俊凯,张俊清
(上海船舶电子设备研究所,上海201108)
0 引 言
直扩信号(Direct Sequence Spread Spectrum,DSSS)具有较低的截获概率和较强的抗衰落能力,且易于组网,因而被广泛应用于水声网络通信中[1]。非合作条件下的水声直扩信号因其低功率谱密度特性使得检测十分困难[2]。
传统自相关法通过将接收信号与自身延时后的信号作相关积分处理并搜索相关峰达到检测的目的,在低信噪比条件下,相关峰容易被噪声淹没,不易提取。文献[3]在自相关检测法的基础上,提出一种基于分段集平均区域统计量的改进自相关检测方法,相较于传统自相关检测法,信噪比容限降低了约3 dB。
本文提出一种基于广义互相关的水声直扩信号检测方法。由理论分析可知,广义互相关加权函数能够增强信号中信噪比较高的频率成分,锐化相关峰,抑制噪声[4-5],且广义互相关运算在频域进行,可以通过快速傅里叶变换来提升算法的效率。通过对相邻分段信号互相关估计结果采用非相干积累平均二阶矩处理,提取相关峰并与检测门限比较,可以在低信噪比条件下检测到水声直扩信号,具有一定的实用价值。仿真结果和水池试验结果都验证了本文方法的有效性。
1 直扩信号数学模型

2 自相关检测法
由式(3)可知,扩频调制采用的伪随机序列周期性重复,因此直扩信号具有周期性,可利用自相关检测法提取周期特征,实现对直扩信号的检测。
2.1 传统自相关检测法
考虑含噪直扩接收信号,如式(7)所示,假设信号s(t)与噪声n(t)互不相关,则含噪接收信号r(t)的自相关函数为
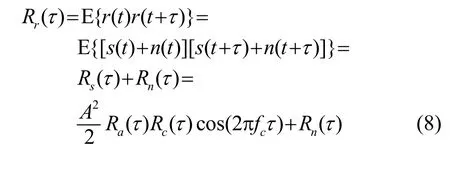
图1是在信噪比(Signal to Noise Ratio, SNR)为-5、-10、-15 dB条件下直扩信号的自相关绝对值平方归一化的结果,扩频码周期为15.5 ms。
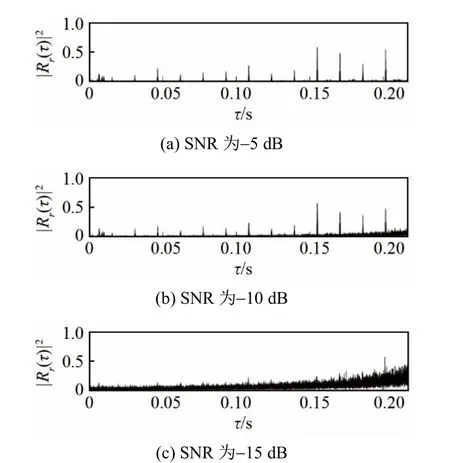
图1 不同信噪比下直扩信号自相关结果Fig1 Autocorrelation functions of DSSS signals under different signal-to-noise ratios
从图1可见,当接收信号SNR较高时,扩频码整数倍周期处会出现相关峰,随着信噪比的降低,相关峰逐渐被噪声淹没,无法检测到直扩信号。
2.2 改进自相关检测法
传统自相关法极易受噪声的影响。在自相关检测法的基础上,文献[3]提出一种基于分段集平均区域统计量的改进自相关检测方法。图2为改进自相关检测法流程图。
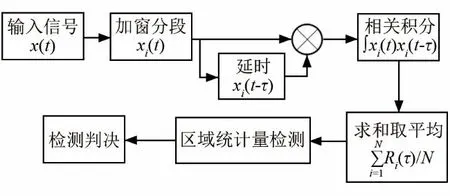
图2 改进自相关检测法流程图Fig.2 Flow chart of improved autocorrelation detection method
将接收信号利用窗函数分段,相邻信号段允许重叠[3],N段信号分别为xi(t),i= 1,2,… ,N,Ri(τ)为第i段信号自相关结果,对每段信号分别进行相关积分并求和取平均得到检测函数J(τ):

改进自相关检测法相比于传统自相关检测法,信噪比容限能够降低约3 dB。
3 广义互相关检测法
广义互相关的概念来自于时延估计。通过求出两个信号的互功率谱,采用加权函数对互功率谱给予一定的权重进行前置滤波,以增强信号中信噪比较高的频率成分,抑制噪声的影响[4],最后通过逆傅里叶变换变换到时域,得到信号的互相关函数。加权函数的意义在于能够使相关峰得到锐化,提高检测性能[5]。
3.1 广义互相关

图3是在信噪比为-5、-10、-15 dB条件下直扩信号的广义互相关绝对值平方归一化的结果,扩频码周期同样为15.5 ms。
与图1传统自相关估计结果相比,能够看出当信噪比为-15 dB时,图3中相关峰仍然清晰可见,表明广义互相关的检测性能更好。且广义互相关运算在频域进行,可以通过快速傅里叶变换来提升算法的效率。
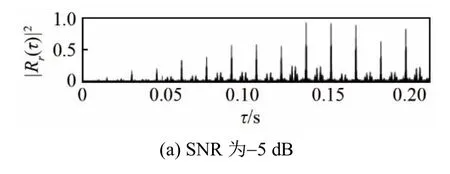
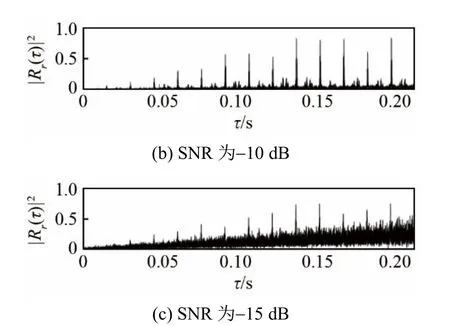
图3 不同信噪比下直扩信号广义互相关结果Fig.3 Generalized cross-correlation functions of DSSS signals under different signal-to-noise ratios
3.2 非相干积累平均二阶矩
由于实际检测时间为有限长,信号的自相关为估计值,传统自相关检测法极易受噪声的影响,当信噪比较低时,一些相关峰会被噪声所淹没,难以得到检测统计量。
本文在时域相关法的基础上,首先将接收信号分段,分别计算相邻信号段的广义互相关估计,经过N次非相干积累平均后,由于噪声之间的非相关性,噪声的方差将减小为原来的1/N,而信号互相关峰值不变,因此可以通过非相干积累提高检测性能[6]。由于直扩信号受BPSK调制的影响,相关函数存在负值,因此,用非相干积累平均互相关二阶矩来消除负值的影响,定义为
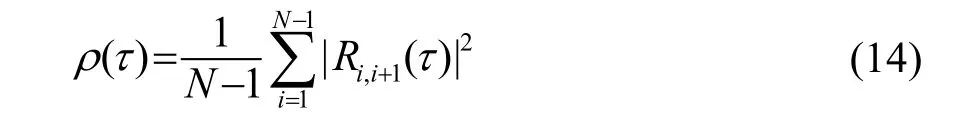
其中:N为信号的分段数;为第i段和第i+1段信号的广义互相关结果绝对值的平方。
3.3 相关峰提取
非合作水声直扩信号的参数是未知的,当信噪比较低时,相关峰受噪声的影响,极容易造成误判[7]。当不能准确判断相关峰间隔时,容易错误提取噪声峰值作为检测统计量。
非合作检测中,由于扩频码的周期Tb未知,无法在相关函数中按照间隔Tb提取相关峰。本文采用相关峰提取方法,不仅可在低信噪比条件下得到检测统计量,而且能够实现相关峰的自动提取[7]。假设扩频码周期为,根据式(15)可知,当时,检测统计量取最大值。
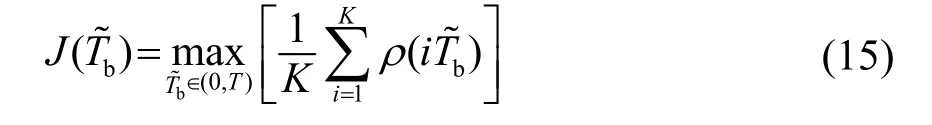
其中:T为假设的最大扩频码周期;K为提取的相关峰个数;ρ为接收信号非相干积累平均互相关二阶矩。
3.4 本文算法原理
结合3.1~3.3节,本文提出一种非合作水声直扩信号检测方法,具体流程框图如图4所示。
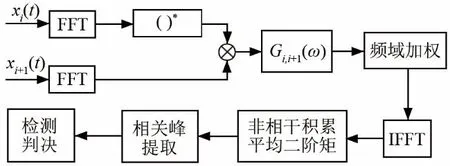
图4 本文检测方法流程图Fig.4 Flow chart of the proposed detection method
算法具体步骤如下:

4 仿真分析与水池试验
4.1 仿真分析
仿真参数如表1所示。仿真中一个码元的采样点数为 1 488,分段数据长度通常为一个码元采样点数的 5~20倍。因此仿真中设置分段数据长度M=22 320,分段数K=12。
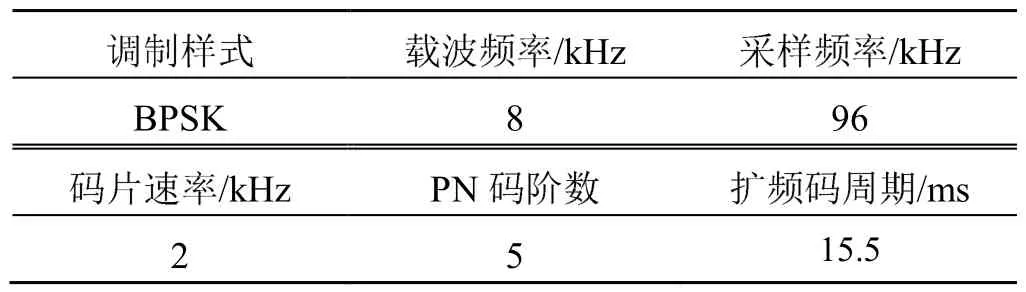
表1 发射信号仿真参数Table 1 Simulation parameters of transmitting signal
为了确定检测门限,生成与接收数据长度相同但功率不同的高斯白噪声,使得信噪比分布为-25~0 dB。同时假设信号不存在和存在两种情况下相关峰均值和相关域整体幅度均值的比值分别为[8]。

利用上述方法分别得到自相关检测法、改进自相关检测法和本文方法在不同虚警概率下的检测概率,如图5所示。
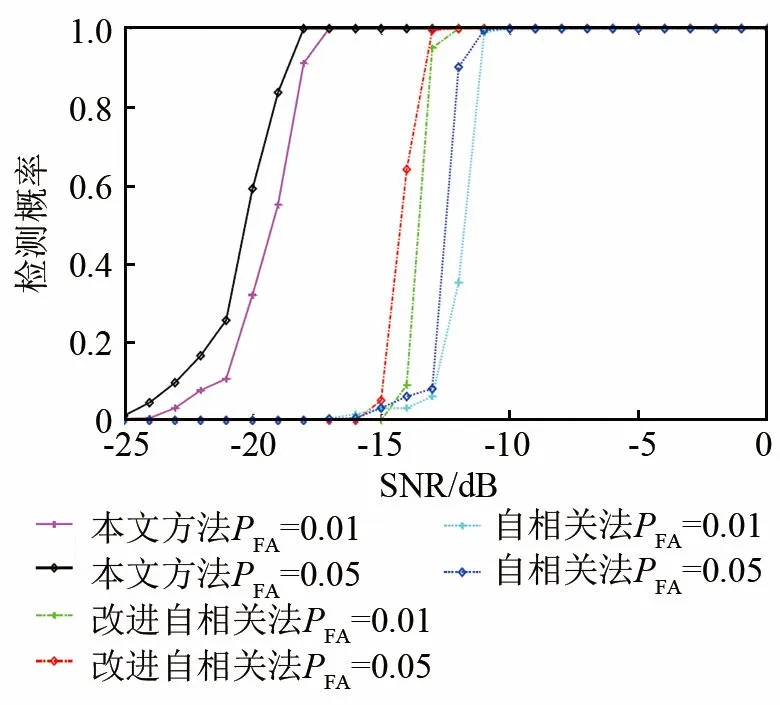
图5 不同虚警概率时三种方法检测概率比较Fig.5 Comparison of detection probabilities of three methods under different false alarm probabilities
分别研究了自相关检测法、改进自相关检测法和本文方法在虚警概率为0.05和0.01时,直扩信号的检测概率随信噪比的变化曲线。虚警概率相同时,本文方法相比于改进自相关检测法信噪比容限降低了5 dB,对直扩信号的检测性能大大提升。在虚警概率为0.05时,本文方法在信噪比大于-18 dB仍能获得很好的检测效果。
4.2 水池试验
通过水池试验来验证本文方法的有效性。在试验中,确定检测门限的方法是:在接收机检测信号前,采集1 000段与接收信号长度相同的环境噪声,采用与接收信号相同的算法参数,分别计算每段噪声相关峰峰值和相关域整体幅度均值的比值,对比值进行降序排列,在给定的虚警概率条件下,根据式(18),确定检测门限。
发射信号参数如表1所示。发射换能器和接收换能器间距为 6 m,布放深度为 3 m,水池平均深度为8 m。图6为接收信号时域波形。
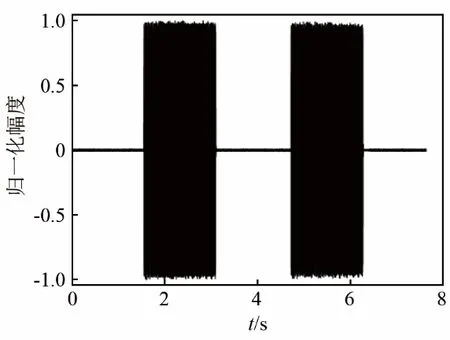
图6 接收信号时域图Fig.6 Time domain graph of received signal
图7为本文检测方法处理结果,处理中设置分段数据长度M=22 320,分段数K=3。
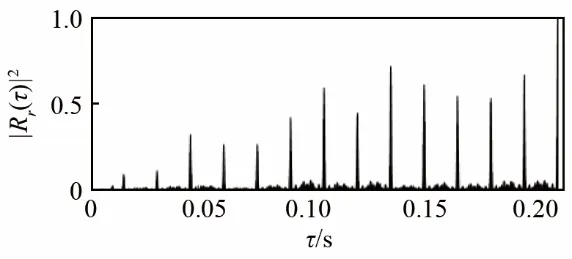
图7 本文方法处理结果图Fig.7 The processing result of the proposed method to the received signal
由于水池环境噪声较小,可以通过对试验接收信号叠加高斯白噪声来重构信号,验证低信噪比条件下本文方法的检测性能。利用式(19)来估计叠加高斯白噪声后待检测信号的信噪比RSN:

图8为对接收信号叠加高斯白噪声后,信噪比为-15 dB时本文检测方法的处理结果。
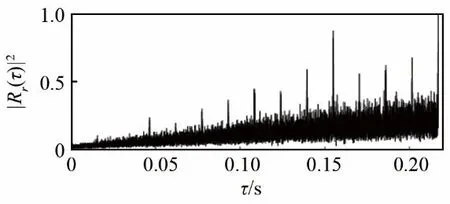
图8 SNR为-15 dB时本文方法处理结果Fig.8 The processing result of the proposed method to the received signal with a signal to noise ratio of -15 dB
从图8可以看出,叠加高斯白噪声后,在信噪比为-15 dB时,相关峰仍然清晰可见,验证了本文算法的有效性与实用性。
5 结 论
本文提出了一种基于广义互相关的水声直扩信号检测方法。通过广义互相关加权运算,可以锐化相关峰,抑制噪声。通过对相邻分段信号互相关运算结果采用非相干积累平均二阶矩处理并提取相关峰,可以实现低信噪比条件下的水声直扩信号检测,具有一定的实用价值。仿真结果和水池试验处理结果都验证了本文方法的有效性与实用性。

