信息源在香浓熵及邓熵中的应用原理

摘 要：在量子决策中，一个事件发生的概率无法单一使用实数来表示。从薛定谔的猫到人类决策。一个事件伴随着多种状态。故需要引入复数来表示这类事件，它也被叫做信息源。香浓熵及邓熵作为一种信息融合方式，表示一组数据的相关程度，混乱程度。用信息源表示邓熵，要解决复数在香浓熵和邓熵公式中的运用，以及所得结果的数学意义。

关键词：量子决策;信息源;香浓熵

一、复数概率的量子性

量子概率来源于量子物理，但不一定要用来描述微观粒子，而是去描述更一般的宏观系统，如人类的认知现象。从数学的角度上来讲，就是将概率取复数这个特点切入到量子概率的理论体系中。量子概率可以说是将经典概率扩展到复数域之后的数学产物，故整个量子概率体系的结论都可以自然得到。

量子概率可以解释成经典概率在复数域的扩充，其实刻画的是观察者对于外界信息的不确定情况下的描述。这种不确定要比经典概率不确定更不确定：一个是量子概率考虑到了观察对观测系统的影响，也考虑到观察者处理信息能力的极限。

量子概率的最主要的特点是不兼容属性-指一个客观物体所具备的两种属性，这两种属性不能同时得到确切的测量值。其中可以用不确定性原理来解释。具体说是我们对两个属性 A 和 B 的认识存在着局限性，如果我们对 A 取某值的信念程度越高，我们对 B 取值的看法就会变得更模糊不清。

例如，由于我们人类的观察、信息处理能力有限，在某一个特定时刻，我们掌握了 A 属性的性质，也就必然会伴随着对 B属性的不掌握。如我们看到了月球的正面，就看不到其反面。故正反面就构成了一对不兼容的属性，并呈现出不确定的关系。

二、信息源在量子化DS证据理论中的形态

Dempster-Shafer证据理论作为对处理未知的信息与模型的时候要比经典证据理论更加灵活。这种未知与量子概率的不确定性相似。因此，在识别框架下的mass（质量）函数除了可以用DS证据理论表示，还应可以在量子理论基础上进行表示。

量子识别框架下的mass函数：

如图所示，要用信息源（|q1>与|q2>）表示一个证据事件对于两个信念|A>与|B>的支持度。

量子框架下的mass函数与DS类似：

Q（|A>）=γeiθ   Q（Φ）=0

其中量子框架下的mass函数Q（|A>）也可以被称作QBPA，叫信息源。

三、香农熵和邓熵的介绍

香农信息熵，解决了对信息的量化度量问题。一条信息的信息量大小和它的不确定性有直接的关系。比如我们要搞清楚一件非常不确定的事，就需要了解大量的信息。相反，如果对某件事已经有了较多的了解，我们不需太多的信息就能把它搞清楚。从这个角度，我们可认为，信息量的度量等于不确定性的多少。

香农熵 H（U）=E[-logpi]=-Σni=1PilogPi

该公式表示，变量的不确定性越大，熵就越大，所需要的信息量也就越大。

香农熵可以度量一个概率分布的不确定度和信息容量，是信息论的基础。证据理论中的基本概率指派（Basic Probability Assignment， BPA），作为视作对概率分布的一种推广。如何度量BPA的不确定度和信息容量，仍然是一个有待解决的问题。针对该问题，提出了一种基本概率指派的熵—邓熵。

Ed （m） = -A    X m（A）log2 m（A）/2|A|-1;

当BPA从幂集退化为单子集上的概率分布时，邓熵退化为香农熵。

四、香浓熵与邓熵在mass函数中的应用与区别

Ed （m） = -A    X m（A）log2 m（A） /2|A| - 1

给出一个识别框架 X = {a， b， c}，已知它们的质量mass函数值为 m（a） = m（b） = m（c） = 1/3， 得到香浓熵和邓熵均为1.585：（香浓熵和邓熵在单子集所得的结果一致

给定一个辨识框架 X={a，b}，对于这个辨识框架的质量函数为m1（a，b）=1

则邓熵表示为

Ed （m）=-log21/22-1

此时无法用香农熵来表示。

五、香农熵与邓熵的信息源表示

在辨识框架Ω={|A>，|B>，|C>}下，有单元素信息源如下

Q（|A>）=0.574eiθ1

Q（|B>）=0.574eiθ2

Q（|C>）=0.574eiθ3

则香农熵邓熵均为

-（0.574eiθ1log20.574eiθ1+0.574eiθ2log20.574eiθ2+0.574eiθ3log20.574eiθ3

根据对数公式和欧拉公式可以得出

-0.574eiθlog20.574eiθ=-0.574（cosθ+isinθ）[ln（0.574）+i（θ+2nπ）]

展开得到

-0.574[ln（0.574）（cosθ+isinθ）+θ（icosθ-sinθ）]

-0.574[ln（0.574）ejθ+θe-i（θ-1/2π）]

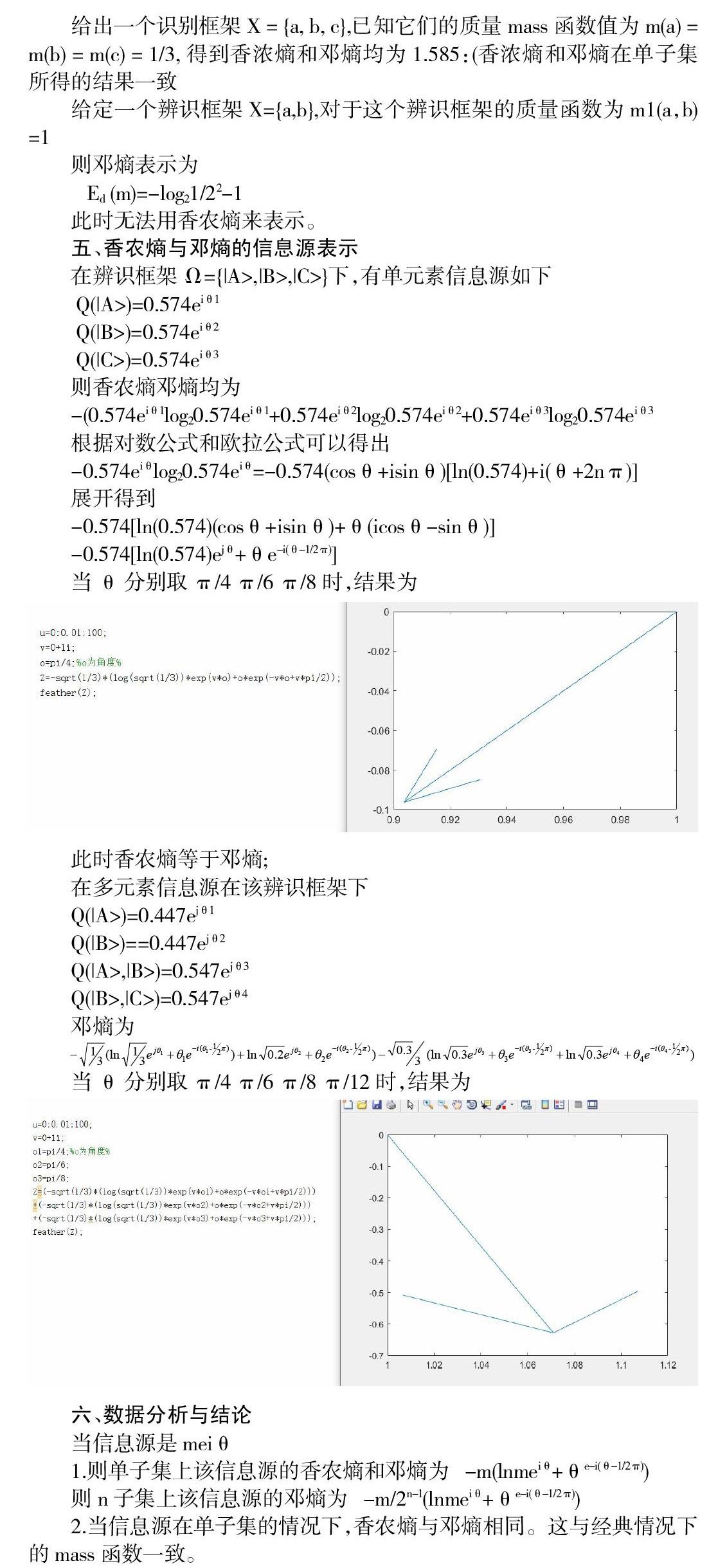
当θ分别取 π/4 π/6 π/8时，结果为

此时香农熵等于邓熵;

在多元素信息源在该辨识框架下

Q（|A>）=0.447ejθ1

Q（|B>）==0.447ejθ2

Q（|A>，|B>）=0.547ejθ3

Q（|B>，|C>）=0.547ejθ4

邓熵为

当θ分别取 π/4 π/6 π/8 π/12时，结果为

六、数据分析与结论

当信息源是meiθ

1.则单子集上该信息源的香农熵和邓熵为   -m（lnmeiθ+θe-i（θ-1/2π））

则n子集上该信息源的邓熵为   -m/2n-1（lnmeiθ+θe-i（θ-1/2π））

2.当信息源在单子集的情况下，香农熵与邓熵相同。这与经典情况下的mass 函数一致。

而信息源扩充到多子集的时候，只有邓熵可以表示该信息源。

3.关于θ的探究

每个信息源而言，θ独立，变化范围在0-360之间。

θ与m无具体的联系，且与概率信念无关，表示的并不是信息源与坐标轴的夹角。

参考文献：

[1]X.Z. Gao and Y.Deng ”Quantum model of mass function” WILEY Int J Intell Syst. 2020;35;267-282.;

[2]Y.Deng “不确定性度量的新方法” 陕西西安：陕西师范大学. 2019.6.18

[3]Pan Y， Zhang L， Li Z， Ding L. Improved fuzzy bayesian network‐based risk analysis with interval-valued fuzzy sets and d‐s evidence theory. IEEE Trans Fuzzy Syst. 2019：1-1. https：//doi.org/10.1109/TFUZZ.2019. 2929024

作者简介：

刘荣政（2001.06- ）男，汉族，辽宁沈阳人，西南大学计信院自动化专业，本科在读，主要研究方向為信息融合与决策。