分布式电源对配电网距离保护的影响及优化
付文秀,高 路,张学瑾
(上海船舶设备研究所,上海 200031)
0 引言
分布式发电(Distributed Generation,DG)作为一种具有竞争力的发电方式,因投资省、能耗低、清洁环保、供电灵活等优势,在现代电力系统中的地位越来越重要[1]。但当DG接入配电网后,配电系统不再是简单的单电源网络,大量的 发电机和负荷同时存在,配电系统中的潮流方向理论上可以是任意的,这势必要影响配电网保护的灵敏性和选择性[2-4]。目前,DG接入配网后保护方案归纳起来大致有3种:1)应用发达的通信网络实现配电网保护间信息交换,如文献[5],利用广域保护技术和电流综合幅值的比较将故障范围缩小到1个故障搜索区域之内,然后利用该区域电流间的相位关系对故障线段进行定位,但该保护方案在较高程度上依赖于通信网络,一旦通信失效,整个保护系统也随之失效,况且就目前我国配网实际建设情况而言,若要实现发达可靠的通信网络,还得投入大量财力物力,需要很长一段时间;2)对配网中采用的传统电流保护方案进行改进,通过复杂的算法和判据来提高保护性能,包括采用自适应保护原理[6]、加装方向元件[7],接入故障限流器[8]等,该方案不需要太多的硬件投入,但对于量大、点多、面广的配电系统而言,安装维护过于复杂,且保护装置之间的定值整定以及配合都相当繁琐,无法在DG高渗透率下的配电系统内广泛使用;3)将输电线路中成熟的保护原理、方案应用于配电系统中。输电线路中的保护原理相对于配电网中的电流保护更加完善,在DG高渗透下采用改进的距离保护不失为一种有效的保护方案。
DG的种类很多,按照运行方式的不同一般可以将其分为传统旋转电机型DG和逆变型DG(IIDG)。传统旋转电机型DG与传统发电机的特性一样,可以等效为电势源与阻抗的串联;IIDG则与之有很大不同[9-10]。本文研究分布式电源对3段式距离保护的影响,在此基础上,结合含IIDG配电系统故障时的特点,考虑IIDG并网时最大输出电流受限于DG容量的影响,分2两种情况探讨了分布式电源的优化策略。
1 分布式电源对距离保护的影响
距离保护是一种反映测量阻抗数值的下降而动作的保护,测量元件都具有明确的方向性,相对于电流保护性能更加完善,因此适合将其应用到含分布式电源的配电网[11]中。距离保护的整定阻抗,用Zset表示;当保护的测量阻抗Zk<Zset时,保护动作。为了分析分布式电源对距离保护产生的影响,以图1所示含DG的放射性配电网络为例,讨论3段式距离保护在DG容量不变而接入系统位置变化和DG接入位置固定而容量变化时所受的影响。

图1 含DG 的放射性配电网络
1.1 距离Ⅰ段
距离保护Ⅰ段瞬时动作,其整定值必须躲开下一段线路出口处故障时阻抗继电器的测量阻抗。距离保护Ⅰ段整定阻抗为

由此可见,距离保护同时反应电压量和电流量,当有DG产生助增作用时,继电器的测量电流增大,相应的测量电压也增大,因此,可以认为无论DG机组的接入位置和容量是否变化,其对原有距离Ⅰ段保护均无影响。但是距离保护Ⅰ段只能够保护本线路全长的80%~85%,必须依靠距离保护Ⅱ段保护线路全长。
1.2 距离Ⅱ段
距离保护Ⅱ段的整定按照与相邻线路距离保护Ⅰ段相配合,并且考虑到分支系数Kb的影响的原则整定,即

如图1所示,DG接于母线C处时,保护1、保护4处的测量阻抗由于不受DG分支作用的影响,距离保护Ⅱ段能够正确动作。保护3受DG助增分支的影响,如图1所示,当在αZ4(α为短路点到母线C的距离占CD段总长的百分比)处发生短路故障时,保护3继电器的测量阻抗为
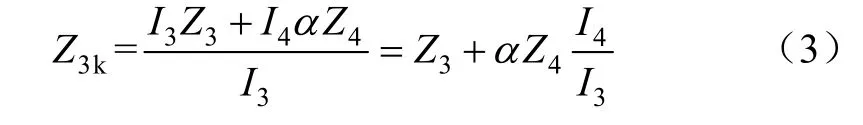
此时流过短路点的电流由主电网和分布式电源共同提供。分流原理为

式中:ZG、ZS分别为DG和系统的等效阻抗值。
记DG额定容量为SG,额定电压为U,则DG满足式

当DG从母线D处接入时,保护1、保护2、保护3均不受DG分支作用的影响,距离保护Ⅱ段能正确动作。保护4由于DG助增分支的作用,当DE段末端短路故障时的测量阻抗为

保护4的测量阻抗增大,且随DG容量的增加,距离保护Ⅱ段灵敏度降低。
DG从母线B、母线E及母线F处接入时同理可分析,从母线A处接入时各保护均不受影响。
1.3 距离Ⅲ段
配电网距离保护Ⅲ段整定值通常按照按照躲开最小负荷阻抗minLZ来整定,其整定值为

因一般DG机组的容量都很小,向距离保护Ⅲ段提供的助增电流也很小,并且距离保护Ⅲ段能够从时限上躲过DG助增电流对它的影响,因此可认为分布式电源的接入对距离保护Ⅲ段基本无影响。
2 分布式电源的并网特点
使用逆变器控制方式的分布式电源并网时,发电单元都是通过一个直流部分连接电容器与逆变控制装置连接再接入电网的,该电容器通过吸收或释放能量来抵消快速的暂态过程,直流电压通过逆变器转换为三相交流电压[12]。逆变型分布式电源不同于传统旋转电机型DG,不能简单地等效为电势源与阻抗的串联,IIDG在并网运行时一般采用电流型PQ控制方式,即通过调节有功电流、无功电流使其跟踪参考电流,对逆变器输出功率的控制问题转化为对电流的控制问题,只要实现对参考电流的跟踪,也就实现了对参考有功和无功的跟踪,采用这种控制方式的IIDG,其供出电流是三相平衡的[13]。图2为采用PQ控制方式的分布式电源并网系统结构图。其中,前端直流部分与单相系统相同,通过三相逆变器和滤波器将直流电能转化为满足并网标准的工频交流电能,经隔离变压器并入中低压电网的公共连接点(PCC)。
因此,在进行短路电流计算时,可以假定逆变型分布式电源在故障后输出功率是不变的。另外在逆变器的控制装置中,大部分都有一个电流限制装置,该装置能够调整DG的输出电流使其保持在某一定值以内[14]。
图3所示的仿真结果验证了这一点。仿真结果表明,对于不同容量的DG,其输出的最大短路电流的受限值不同。

图2 分布式电源并网系统结构图

图3 PI限幅增大时某短路电流
3 基于距离保护的DG 的优化策略
配电网中分布式电源的接入主要对距离保护Ⅱ段的灵敏度产生影响,并且其影响程度随DG位置和容量的改变而改变,因此采用距离保护时有必要对DG进行优化。考虑DG输出的短路电流受限于某一定值,即受最大输出短路电流的影响,以下分2种情况进行分析。
3.1 不考虑DG 最大输出短路电流的影响
此种情况主要是适合于DG输出的短路电流未到达所对应的定值。

联合式(9)~式(12),得到关于DG容量和位置的目标函数以及约束条件:


3.2 考虑DG 最大输出短路电流的影响
对应于一定容量的DG,其输出的短路电流不能超过某个定值,设为IM。图1中,记CD段的线路长度为L4,当在线路CD段αL4(α为短路点到母线C的距离占CD段总长的百分比)处发生短路故障时,DG的输出的短路电流为

式中:E为电源电动势。
考虑DG受限于其最大输出短路电流,可令GM=II,得到对应于DG输出最大短路电流时CD段距离保护的测量阻抗值:


从选址的角度来考虑时,令x=Z4或者x=Z3代入式(18),同样,求出x的范围后,由于x只能取各段线路阻抗值,需根据这些离散点进一步确定x的取值,最终确定DG的合适接入位置;从定容的角度来考虑时,由于DG容量SG与IM有关,令x=IM代入式(18),求出IM的范围后,需根据SG与IM的实际关系,选定DG的容量。
在对DG进行优化计算时,对是否会发生2种情况下对应的优化关系式(13)和式(18)所包围的区域相互越界的情况分析如下:由式(13)、式(15)和式(18)可以看出,计算的优化方向为目标函数f(x)增大的方向,不妨首先设Z4''≤Z4',即DG输出的短流电流已达到受限值IM,此时应采用DG的优化算法关系式(18),可以看出,随着f(x)的逐渐增大,Z3逐渐减小,Z4逐渐增大,而Z4逐渐减小,计算情况会逐渐趋于越界,进入关系式(13)的区域范围内,即Z4''>Z4',此时随着f(x)的增大,Z3逐渐减小,Z4逐渐增大,但不会再出现Z4''≤Z4'的情况。可以看出,此时如果再考虑DG容量选择的问题,则有可能又使得优化方向由关系式(13)返回到式(18)的范围内。
因此,在对DG进行选址定容时,首先要进行DG容量的选择,容量确定后,再按照式(15)考虑DG最大输出电流受限的情况计算,然后进行选址判断。如果计算结果落在关系式(18)所包围的区域内,则在优化计算时有可能要进入关系式(13)的区域内继续优化;而如果进入到关系式(13)所包围的区域内,则不会再返回到关系式(18)的区域中,此时在关系式(13)区域范围中的解即为最优解。
4 算例分析


图4 某10 kV 配电系统
1)DG接于母线B处,如图4所示,其容量SG在0~50 MVA内变化,当BC末端(k处)发生三相短路故障时,保护1、保护2的测量阻抗值Z1k、Z2k如表1所示。其中,DG容量为0,表示未加入DG时原配电网的阻抗参数。
由表1可以看出:保护2的测量阻抗值保持不变,不受DG并入的影响;保护1的测量阻抗值随DG出力的增加而增加,对于原配电网,保护的整定值不变,因而保护1距离保护Ⅱ段的灵敏度降低。
2)DG固定接于母线B处,其容量SG在0~50 MVA内变化,保护1距离保护Ⅱ段的整定值及灵敏度随其出力的变化关系如表2所示。
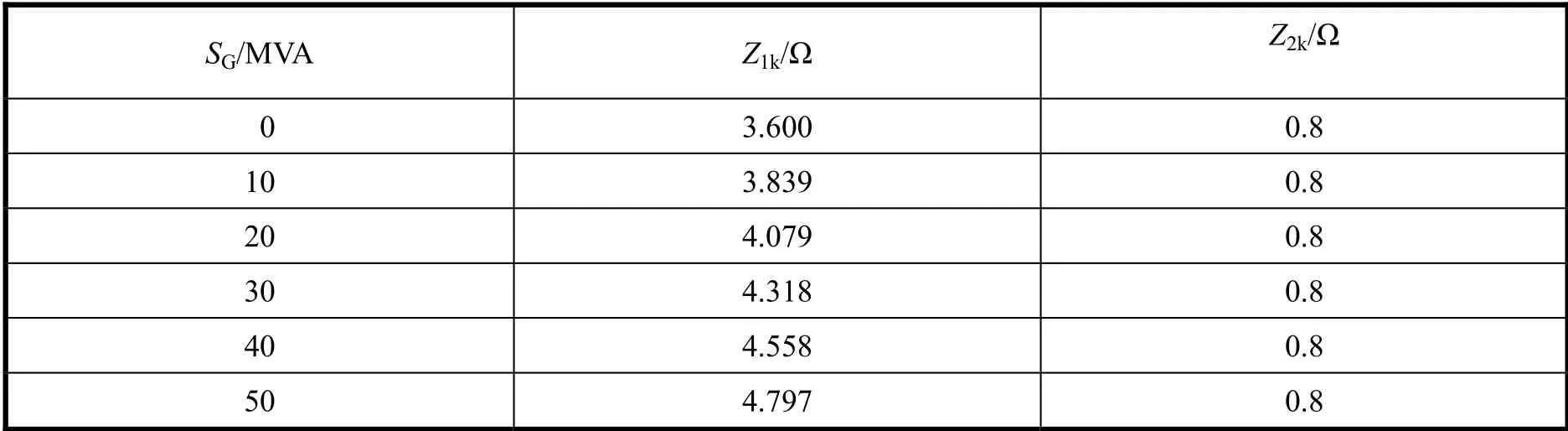
表1 各保护测量阻抗值与DG 出力变化关系

表2 保护1距离保护Ⅱ段整定值及灵敏度与DG 出力变化关系
由表2可以看出:当DG容量在0~50 MVA内变化时,保护1距离Ⅱ段的灵敏度随DG出力的增大而增大,但DG容量小于40 MVA时保护的灵敏度均小于1.25,不满足要求;当DG容量为50 MVA时,灵敏度大于1.25,满足要求。因此,对于本例的配电网,DG的容量可选取50 MVA及以上。


表3 DG 容量为10 MVA 时的最大输出短路电流及相应的测量阻抗值



表4 DG 容量为50 MVA 时的最大输出短路电流及相应的测量阻抗值

5 结论
鉴于对传统配电网保护进行整定值修改的复杂性,本文提出将输电线路中较为成熟的距离保护应用于含分布式电源的配电系统中,分析了DG位置和容量变化对3段式距离保护的影响,结果表明DG的并网主要影响距离保护Ⅱ段的灵敏度。在此基础上,根据逆变型DG的并网特性,考虑其接入配电网后短路电流与DG容量的对应关系,分2种情况提出了DG的优化策略,即通过保证DG接入前后距离保护Ⅱ段的灵敏度来对DG进行选址定容。结合PSCAD仿真软件,通过某10 kV配电系统进行仿真分析,验证了该优化策略的有效性和可行性。

