基于初始化非负矩阵分解的光伏发电预测

彭 飞，张健男，张晓华，王汉军，吴 奕，陈志奎

(1.国家电网公司 东北分部，辽宁 沈阳 110180；2.中国科学院 沈阳计算技术研究所有限公司，辽宁 沈阳 110180；3.大连理工大学 软件学院，辽宁 大连 116620)

0 引 言

目前,在光伏发电的预测领域,国内外学者对光伏发电功率的预测做了大量研究,常用且高效的模型主要有以下几种:

第一种是传统预测法，比如回归法[1]、趋势外推法[2]、基于ARIMA[3-5]的系列方法。传统预测方法较为简单，对于变化规律明显、趋势变化显著的气象数据预测能力较差。

第二种是人工智能算法，人工智能算法主要依托各种神经网络[6-10]、支持向量机[11]、小波分析算法[12]，这类算法突破了传统预测法的局限性，近年来得到广泛应用。虽然人工智能算法具有较强的非线性映射能力、处理大量复杂数据的能力以及容错能力，但由于需要进行逐步分层预训练，学习时间较长，若参数选择不当极易陷入局部最优解。

针对上述问题，提出一种基于初始化非负矩阵分解(NMF)的光伏发电预测方法，使用模糊C均值聚类(FCM)[13]的初始化方法，有效解决了NMF算法[14]收敛速度慢和易于陷入局部极小的问题。相比于其他算法，该算法在一定程度上降低了求解难度，提高了求解速度与预测准确率。

1 相关理论

1.1 模糊C均值聚类算法

模糊C均值聚类算法(FCM)是模糊聚类算法的一种，它具有普通C均值算法的一些特性，不同于普通C均值算法的地方在于其加入了模糊的概念，改进了其性能，通过模糊划分，用一个隶属度来表征数据集中每个对象属于该类的程度，其中隶属度的取值范围为0～1。FCM算法改善了普通C均值算法对于数据对象非A即B划分规则的缺陷，将原来的硬性划分变成柔性划分。

FCM算法将数据集X={x1,x2,…,xn}划分为C个模糊组，矩阵V的元素vi表示聚类中心，矩阵中Q的元素qli表示第l(l=1,2,…,n)项数据属于第i类的隶属度，qli(i=1,2,…,c)满足以下条件：

(1)

∀i,l,qli∈[0,1]

(2)

(3)

其中FCM的价值函数为：

(4)

(5)

上述公式中：m∈[1,∞]为加权指数；dli是样本数据和聚类中心的距离。

1.2 非负矩阵分解算法

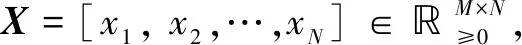
由于求解完全非负矩阵分解(X=UP)是一个NP难问题，并且缺少合适的凸表达式，所以近似非负矩阵分解(X≈UP)被人们广泛使用，因此，许多非负矩阵分解的实现方法是最小化X和UP间的重构误差，这些方法的主要区别在于重构误差的衡量标准和优化过程。

为了量化X和UP间的重构误差，需要先定义一个度量D(X‖UP)。度量D(X‖UP)主要有距离或散度两种形式，不同的度量也决定了目标函数是一个单独的损失函数还是需要同时最小化的一组损失函数。该文采用欧几里得矩阵的平方(SED)来衡量X与UP,对应的目标函数如下:

(6)

式中，‖·‖F表示Frobenuis范数。式(6)中的目标函数J1相对于联合变量(U,P)是非凸的，但是当固定(U,P)中的一个变量，相对于另一个变量，此时J1是凸的。

2 构建初始化非负矩阵分解的光伏发电预测模型

根据光伏发电的特点，结合第一节提到的相关理论,给出基于初始化非负矩阵分解的光伏发电预测方法,包括自适应相似日的选取、模型的搭建与预测。

2.1 自适应相似日的选取

在光伏发电预测的初始化非负矩阵分解的光伏发电预测模型中，相似日的选取是影响预测结果精度的重要影响因素，该文使用自适应的方法对相似日进行筛选，选取流程如图1所示。

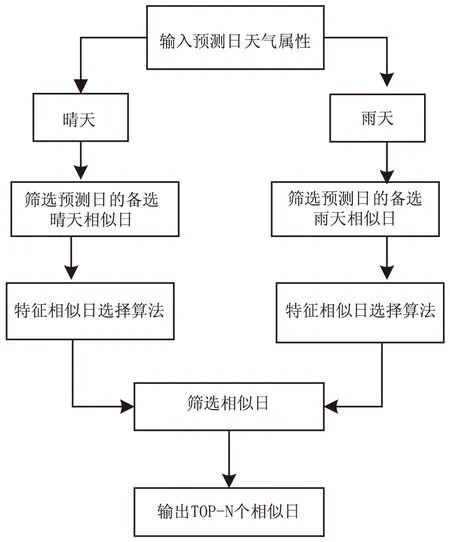
图1 自适应的方法筛选相似日流程

自适应相似日选取的主要步骤如下：首先根据预测日的天气属性(雨、晴)，从预测日之前的历史日筛选出预测日的备选相似日，然后通过特征相似日选择算法筛选最终相似日，特征相似日选择算法是将预测日的日特征向量和备选相似日的日特征向量进行相似度度量，经过该方法筛选出的相似日可以有效提高基于初始化非负矩阵分解的光伏发电预测的预测精度。一般关于光伏发电功率的日特征向量包含气温、太阳辐射度天气类型等因素，设定日特征选择有n个评价因素，则第i日的特征向量表示如下：

xi={xi1,xi2,…,xik,xin}

(7)

为了合理进行相似日的选择,该文采用欧氏距离法求取第j日与第i日的相似度，如下所示：

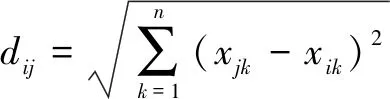
(8)

式(9)的Oij为第j日与第i日的相似程度，α的取值为1/max(dij)。

Oij=1-αdij

(9)

使用上述相关方法对样本数据进行相似日样本筛选，可以计算出与预测日属性最为接近的样本数据，为预测准确性奠定基础。

2.2 预测模型的搭建

将量化后数据作为预测模型的输入，因此利用上节提到的相似日选择算法选取的与预测日天气类型相同、气象特征相近的训练样本对预测模型进行训练。每个相似日属性数据包含最高气温Temp-h、最低气温Temp-l、风力Ave-wind、辐照度Irradiance、光伏实发电量PV-power，预测日中的数据包含已获得的最低Temp-l、最高气温Temp-h、风力Ave-wind和需要预测的光伏发电量PV-power，由于风力Ave-wind、辐照度Irradiance等环境因素是随时间动态变化的，所以在每一个时刻都构建一个预测日-相似日关系矩阵RN×M，该矩阵的前n-1行代表相似日数据，第n行代表预测日数据，该矩阵的前m-1列代表影响光伏实发电量的属性因素，第m列代表光伏发电量，由于预测日的光伏实发电量未知，所以将其初始值设置为0。数据模型建立之后，每个时刻的关系矩阵RN×M通过基于初始化非负矩阵分解的光伏发电预测算法得到预测日每个时刻的预测值，如图2所示。

图2 FCM_NMF的光伏预测模型

2.3 模型的预测

结合FCM和NMF算法，从数据选择的角度提高预测的准确度。首先，考虑天气因素，将预测日分为不同的天气类型；其次，FCM对晴天或者雨天的数据进行聚类分析。最后，结合NMF算法对光伏发电进行精确预测。

图3是光伏发电功率预测框图。

图3 光伏发电功率预测框图

首先将每个时刻tn的关系矩阵R进行FCM聚类，通过式(10)、式(11)分别得到每个时刻关系矩阵R的最优隶属度矩阵Q和聚类中心V；

(10)

(11)

将上述FCM得到的隶属度矩阵Q和类中心V作为NMF分解的初值，然后采用交替式方法进行迭代求解。为了有效地求解NMF的目标函数，采用Lee等[15]提出的著名的乘子更新法，采用简单的乘式迭代方法即可进行求解。对于式(6)，其对应的更新规则为：

(12)

(13)

式中，t表示当前迭代次数。根据上述更新规则，在满足一定次数迭代后算法收敛。

该文提出的初始化非负矩阵分解的光伏发电预测模型具体步骤如下：

输入：根据预测日筛选出相似日每个时刻(t1,t2,…,tn)对应的Temp-h、Temp-l、Ave-wind、Irradiance、PV-power，预测日对应的每个时刻的Temp-h、Temp-l、Ave-wind、Irradiance，并将预测日发电量初始值设置为0。

输出：预测日每个时刻(t1,t2,…,tn)对应的光伏发电量。

Step1：根据预测日构建预测日-相似日矩阵R；

Step2：将每个时刻tn的关系矩阵R进行FCM聚类，得到每个时刻的最优V、Q；

Step3：将每个时刻tn对应的预测日-相似日关系矩阵R进行NMF，并将上步得到的最优V，Q分别对应为关系矩阵NMF参数的初始化的初值，得到每一个时刻NMF的分解结果U,P；

Step4：得到每个时刻tn的NMF分解结果后，对原始模型进行重构，获得每个时刻预测日的光伏发电预测值Predictive value；

Step5：end

3 实验验证

本节使用某省份光伏发电的历史数据作为实验数据集,应用第一节的相关理论和第二节的模型构建方法展开实验验证,主要包括数据准备、实验结果、对比实验分析三部分。

3.1 实验数据集

实验数据选取某省份的光伏发电历史数据。数据包含辐照度、风速、实发电量等实时采集的数据。采样时间范围为2019年1月1日～11月3日。此外，由于光伏发电情况受温度等环境因素影响，在实验中从网络上获取了上述地区在该段时间的历史天气情况，将每天的天气情况也作为实验数据。按照天气类型，分别对晴天和雨天进行预测，选取该省份2019年8月29日(雨天)和9月12日(晴天)作为预测日，根据预测日的天气类型在8，9月份中使用自适应相似日的选取方法，选取了最相近的七个相似日(具体见表1)，并选取该省份温度、风速、辐照度以及光伏发电功率的现场实时测量数据，采样周期为15 min,选取的预测时间段为早上7点到晚上6点15分，即每天46个采样点。

表1 相似日以及预测日

3.2 度量指标

在模型预测效果度量中,采用检验模型较普遍的两个评价指标:均方根误差(RMSE)和绝对误差(MAE),具体表达式如下:

(14)

(15)

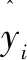
3.3 实验平台和环境

为评价文中算法的有效性，实验所使用的计算机配置如下：2.6 GHz CPU，16 GB内存，在pycharm 2019.3.1环境上实现。

3.4 实验结果

3.4.1 不同天气类型预测结果

将基于初始化非负矩阵分解的光伏发电预测算法应用到雨天(8月29日)和晴天(9月12日)的光伏发电预测中，对两组实验的仿真结果进行了汇总,并对每组46个采样点的仿真结果做了对比显示，如图4和图5所示。

图4 雨天功率预测结果 图5 晴天功率预测结果

3.4.2 结果对比

将初始化非负矩阵分解的光伏发电预测模型(FCM-NMF)与Elman神经网络预测模型[16]、BPNN预测模型[8]、LSTM预测模型[9]进行准确率测评，模型运行结果如图6和图7所示。

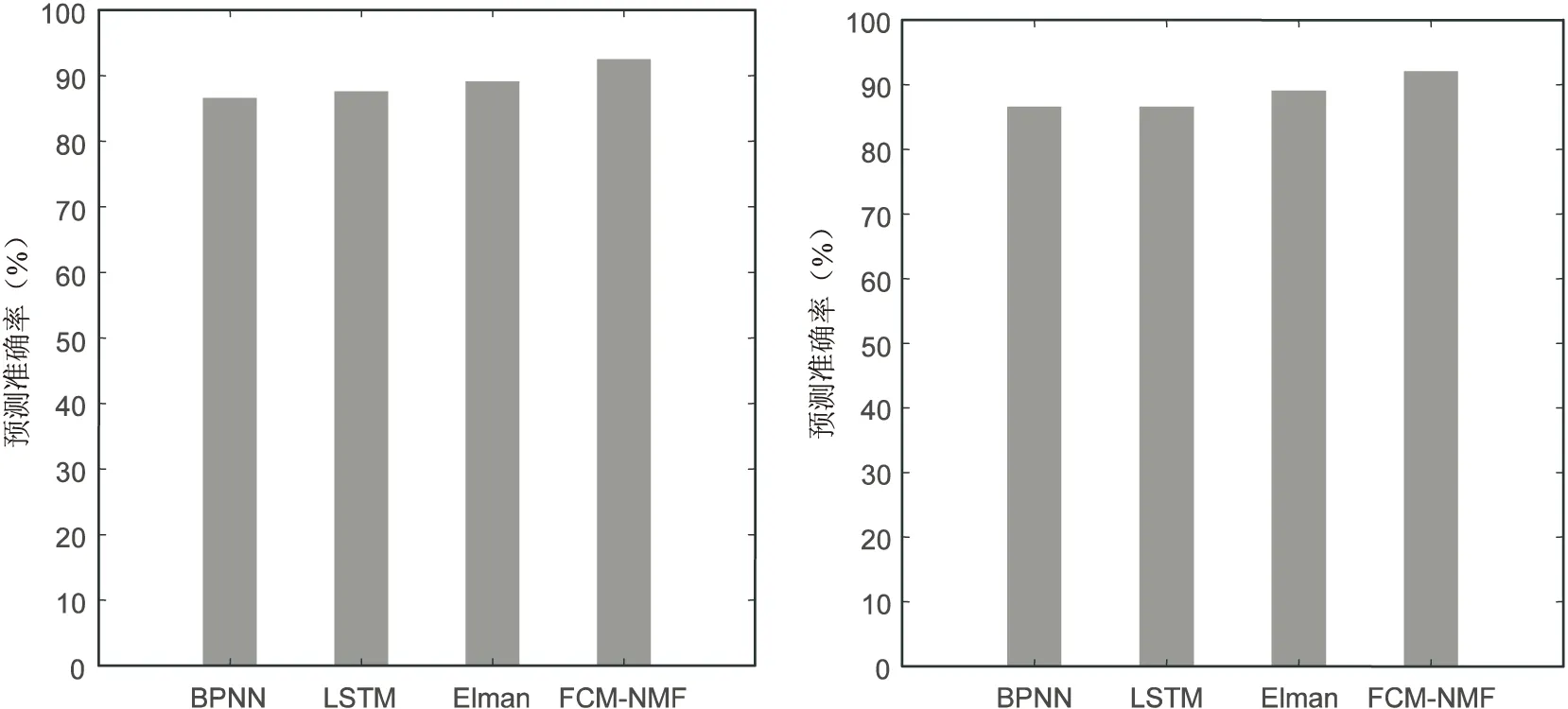
图6 雨天准确率预测结果对比 图7 晴天准确率预测结果对比

为了验证基于初始化非负矩阵分解的光伏发电预测模型在不同天气类型中的预测优势，将该文提出的算法与基本的非负矩阵分解算法(NMF)进行了预测效果度量比较，结果如表2和表3所示。

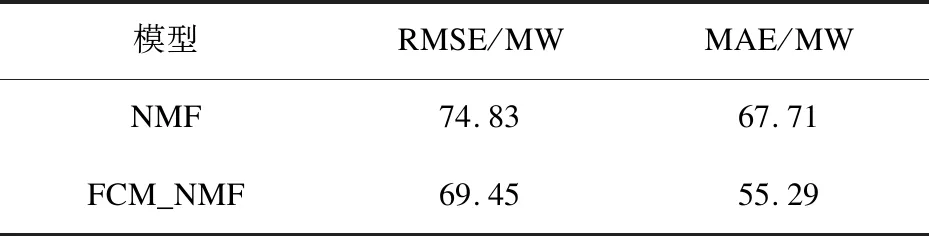
表2 雨天2种预测模型的预测误差统计

表3 晴天2种预测模型的预测误差统计

可见,无论是RMSE还是MAE,由表2与表3对比数据可看出，FCM_NMF的预测精度高于NMF的预测模型。

4 结束语

将初始化非负矩阵分解的方法应用到光伏发电预测中，实现了对预测日某个时刻的发电预测。考虑到天气属性和历史发电对预测日发电的影响，对预测日筛选出的相似日进一步做了划分，最后采用基于初始化非负矩阵分解的光伏发电预测模型进行了预测模型的预测。实验结果表明，最终的预测效果较BPNN等模型有所提高。

总的来说，验证了初始化非负矩阵分解模型在光伏发电预测领域的适用性，扩展了该方向的应用范畴。基于当前的工作，后续将从以下方面继续研究：在筛选相似日的时候，将季节因素的影响考虑在内；寻找有效的方法优化初始化的非负矩阵分解模型，提高预测精度。