钢管混凝土拱桥成桥及施工阶段索力优化研究

杨志魁

摘 要：为确定钢管混凝土拱桥合理成桥索力和施工阶段张拉力的优化方法，以实际工程为背景，通过借助有限元软件Midas Civli和数值分析软件Matlab，并利用最小弯曲能量法初步求解钢管混凝土拱桥的成桥索力，再通过影响矩阵原理对拱桥内力进行调整，进而求解最终成桥索力。对施工阶段索力则是采取正装迭代法，并结合施工阶段的影响矩阵，进而求解施工过程中各吊杆的索力。最后，通过观察成桥索力下拱桥内力、线形是否符合要求，从而确定该方法的可行性。

关键词：钢管混凝土拱桥;最小弯曲能量法;影响矩阵

中图分类号：U448.222     文献标识码：A     文章编号：1003-5168（2021）36-0070-03

Research on Optimization of Cable Force of CFST Arch Bridge During Completion and Construction

YANG Zhikui

（Shaanxi Vocational & Technical College ，Xi'an Shaanxi 710000）

Abstract：In order to study the method of cable force optimization of concrete-filled steel tube arch bridge，this article takes the actual project as the background and uses finite element software Midas Civli and numerical analysis software Matlab to solve the cable force of concrete-filled steel tube arch bridge.In this paper，at first，the minimum bending energy method is used to solve the bridge cable force and then the internal force of the arch bridge is adjusted by the influence matrix principle to solve the final cable force.In the construction stage，the cable force of each boom is solved by means of the formal installation iteration with the influence matrix of the construction stage.Finally，the feasibility of the method is determined by observing whether the internal force and line shape of the arch bridge meet the requirements.

Keywords：concrete-filled steel tube arch bridge;minimum bending energy method;influence matrix

钢管混凝土能兼顾钢管混凝土结构和系杆拱桥的特点而被国内外广泛使用。钢管混凝土拱桥设计过程中，要考虑在吊杆力作用下，系梁和拱肋受力较合理且线形平顺。但是在实际工程中，由于施工过程的复杂性[1-2]，施工时会受到各种因素的影响，甚至会影响到成桥索力。因此，需要正确地给出不同吊杆在施工阶段的索力[3-4]。

本文通过有限元软件Madis Civil并结合Matlab软件，以实际工程项目江東大桥为例，分析验证最小弯曲能量法和影响矩阵法对其成桥和施工阶段索力求解的可行性。

1 索力优化方法

1.1 影响矩阵法

结构设计和施工过程中，会选择任意阶段随机截面进行控制，这些截面被称为关键截面，选取截面上的特性参数作为控制变量，通过这些控制变量判断结构的内力、线形是否合理。为了实现截面目标的调整，引入了影响矩阵这一概念，即当结构满足线形叠加原理时，有：

[CX=D]       （1）

其中[C]为影响矩阵，是指当施调向量第[i]个向量[xi]发生单位变化时，引起受调向量[{D}]的变化量成为影响向量;[X]为施调向量，是指结构中可通过调整来改变受调向量的[l]个独立元素（[l≤n]）所组成的列向量;[D]为受调向量，是指结构中关心截面上[n]个独立元素所组成的列向量。这些元素一般是关心截面的内力、位移。调整这些元素使结构达到期望的状态。

当影响矩阵[C]中[n>l]时，即控制参数的个数多于施调向量中元素的个数时，影响矩阵不为方阵，此时求解该线形方程可通过最小二乘理论近似计算。

令[Qx=CX-D2]，为使[Qx]最小，对[xi]求偏导使[∂Q∂xi=0]。用矩阵表示为[CTCX=CTD]，此时[CTC]为[l]阶方阵，只要保证[C]的列向量线性无关即可近似解出：

[X=CTC-1CTD]     （2）

1.2 最小弯曲能量法

本文中实际工程的成桥索力采用影响矩阵原理下的最小弯曲能量法进行初步求解，其基本原理是当结构中的弯曲应变能最小时，此时的索力值即成桥状态下吊杆的合理索力。结构的弯曲应变能公式如（3）所示：

[U=SM2S2EIdS]       （3）

将结构离散，离散后公式如（4）所示：

[U=i=1mLi4EiIiM2Li+M2Ri]      （4）

式中：[m]为离散单元的数量;[Li]、[Ei]、[Ii]分别为单元的长度、材料的弹性模量和截面惯性矩;[MLi]、[MRi]分别表示单元的左右端弯矩。

将式（4）写成矩阵形式：

[U=MLTBML+MRTBMR]   （5）

其中，[ML]和[MR]分别表示左右端弯矩组成的向量;[B]为对角系数矩阵，且对角元素为：

[bii=Li4EiIi][i=1，2，...，m]     （6）

根据影响矩阵的原理，令调索前单元的弯矩向量为[M0]，施调向量为吊杆索力向量[T]，影响矩阵[C]，则调整后的弯矩为：

[M=M0+CT]      （7）

将式（7）代入式（5）化简得：

[U=C0+M0TBCT+TTCTBM0+TTCTBCT]

（8）

其中，[C0]是与[T]的无关常数。

当结构的弯曲应变能最小时满足：

[∂U∂Ti=0][i=1，2，3，...，l]    （9）

则式（8）求导后并用矩阵表示为：

[CTBCT+CTBM0=0]   （10）

至此，最小能量法索力优化问题就转化成线形方程组的求解问题，对于此线形方程组的求解，可以通过数学软件编辑计算程序。但实际求解过程可以通过有限元软件进行快速近似求解。由于公式（10）与力法方程表达形式类似，区别在于力法方程考虑了弯矩、轴力和剪力的影响，而公式（10）仅考虑了弯矩的影响。假如将结构各单元的抗弯刚度[EiIi]人为缩小[ξ1]（[ξ1]为较大的某数，如1 000），或将轴向刚度[EiAi]扩大[ξ2]倍（[ξ2]为较大的某数，如10 000），力法方程便可忽略轴力、剪力项进而仅考虑弯矩项的影响。

1.3 正装迭代法

正装迭代是按照实际施工顺序对实际工程进行施工阶段的仿真模拟，相比倒装迭代，其能较好地模拟实际过程，且能考虑施工中的非线性因素。其具体步骤是先确定一组迭代初始值，然后将该初始值代入模型中循环迭代，最终与目标索力闭合。迭代的初始值理论上可以为任意数值，但单纯地利用正装迭代计算量相对较大，且迭代次数一般较多，这在实际应用中会比较烦琐。因此，初始值不妨先利用倒装法初步求得，以该初始值作为第一次迭代的索力值，在每次迭代后先求出该阶段的影响矩阵，然后根据影响矩阵原理微调，将调整后的结果作为下一次迭代的初始值，可极大地减少迭代次数，提高计算效率。

2 算例分析

2.1 工程概况

本文钢管混凝土拱桥为预应力混凝土系杆拱结构，采用刚性系梁刚性拱，计算跨径L为126.28 m，拱轴线为二次抛物线。拱肋采用哑铃形钢管砼，内充C50微膨胀砼。系梁采用箱形断面，每一系梁内设有24束预应力束。桥面2%横坡通过横梁高度的变化进行调整，风撑采用K型，主桥桥面设10 cm现浇整体化混凝土。每片拱肋設吊杆19根，由于吊杆为对称结构，为了便于计算，将同一对称部位的吊杆取相同编号。

2.2 参数设置

本文拱桥实例采用有限元软件Midas进行模拟，全桥共760单元。拱肋采用梁单元模拟，并采用施工阶段联合截面模拟拱肋不同施工阶段下的状态。系梁、桥面板均采用梁单元模拟，吊杆采用桁架单元模拟。拱脚采用简支边界条件，施工阶段吊杆力为体外力输入方式。主要模型材料特性见表1。

2.3 成桥索力优化

采用最小弯曲能量法计算成桥索力时，将结构各单元的抗弯刚度缩小1 000，做一次落架计算。得到初始索力之后再利用影响矩阵进行二次调索。调索时把拱脚处和各吊杆与横梁交点处作为控制点，以该点处的弯矩为控制目标，利用Madis软件求解出影响矩阵，并结合Matlab软件计算得到初拉力和最终索力图，如图1所示。图2表示优化前后系梁的弯矩图。

从图1、图2可以看出，先利用弯曲能量法对索力进行初步求解后，再用影响矩阵原理对求得的索力进行二次优化，可以使吊杆满足由短到长索力逐渐增大的特性，系梁弯矩相比于优化前更均匀，且最终成桥索力下的结构受力满足连续梁受力形式。

2.4 施工阶段索力优化

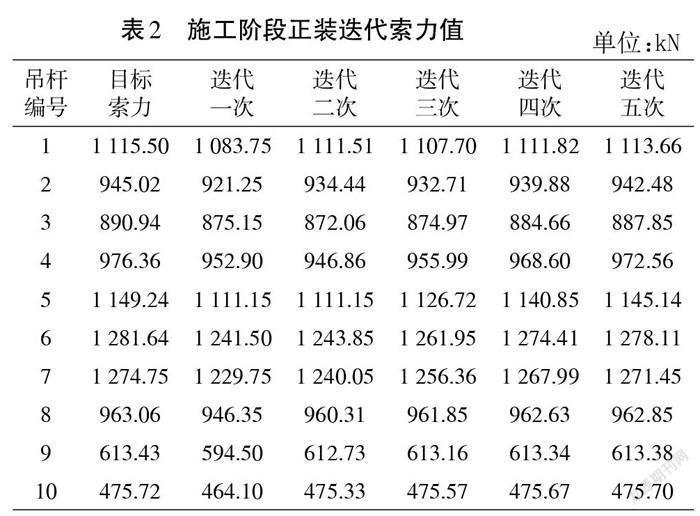
对于施工阶段各吊杆的索力求解方法则是先采用倒装求出一组索力，然后以该索力作为正装迭代的索力初始值，再根据影响矩阵原理对每次迭代后的结果微调，然后将调整后的索力作为下一次迭代的初始值，就这样循环迭代，最终实现闭合。迭代结果如表2所示。

由表2可以看出，本实例采用影响矩阵下的正装迭代计算方法，在仅迭代了5次后，吊杆索力即可接近目标索力，且第一次迭代到第五次迭代，最大误差由3.54%减小到0.01%。由此可得，利用此方法可以较好且较快地求得目标索力值。

3 结语

本文在有限元软件模拟试验的基础上，考虑了系杆拱桥的弯矩和线形，对结构成桥阶段和施工阶段进行索力优化，主要结论如下。

①将弯曲最小能量法与影响矩阵原理相结合，求得成桥状态下的索力满足系杆拱桥内力和线形的要求，且操作方法简便，极大减少了工作量。

②正装迭代法辅以影响矩阵的方法求解吊杆施工阶段索力，不仅能考虑到结构的经济效益，同时还能兼顾施工过程的非线性因素，能够较为准确、高效地得到结果。

本文使用的方法可进一步推广到线性或弱线性结构，在实际工程中有较好的应用前景。

参考文献：

[1] 李晔，李勇，李继军.采用斜拉扣挂法施工的大跨径钢管混凝土拱桥的全过程索力优化计算方法[J].建筑钢结构进展，2019（2）：33-39.

[2] 朱利明，申昆，濮卫，等.空间三索面斜吊杆非对称系杆钢拱桥合理成桥索力优化[J].世界桥梁，2020（6）：54-59.

[3] 周倩，周建庭，马虎，等.钢管拱肋分段吊装扣索一次张拉索力改进算法[J].交通运输工程学报，2020（1）：92-101.

[4] 王祥国，邓博，杨孟刚.考虑施工阶段的高铁系杆拱桥吊杆张拉优化研究[J].铁道科学与工程学报，2020（4）：808-814.