基于动网格与滑移网格技术的隧道列车活塞风计算对比

赵 珀 李 炎 杜 强 韩福成

（兰州交通大学环境与市政工程学院 兰州 730070）

0 引言

隧道活塞风对运营通风起到非常重要的作用。列车在隧道内克服阻力行进的过程中，实现了列车与气流间的能量交换，使隧道内的气流运动，气流的压力和速度发生变化，即产生活塞风。因此活塞风属于自然通风的范畴，最大程度上利用隧道内的自然通风不仅可以降低隧道内环境的温度，还能节省空调能耗，降低运行成本。

由于研究具有一定的特殊性，测量活塞风相关参数需要在隧道内布置测点、安装设备，存在一定危险性和限制性，国内外虽有学者进行实测实验[1,2]，但大都利用理论推导[3-5]、模型试验[3-5]、数值模拟的方式展开研究，近年来，随着流体力学计算软件的逐渐发展，数值模拟研究的方式越来越普遍。国外已经有很多学者利用数值模拟的方法进行相关研究[9-11]。如2014年Gilbert T 等[12]利用动网格技术模拟研究了列车在不同横截面积、不同长度的隧道内运行时产生的列车活塞风大小及变化规律；Gonzalez M L[13]等利用动网格技术模拟了相邻地铁车站间活塞风的影响范围。国内方面，2005年包海涛[13]首次采用动网格技术对南京地铁珠江路站列车运行产生的活塞风对站台内的影响进行了动态研究，推动了我国进一步开展隧道空气动力学的研究进程。近年来，崔景东[15]利用滑移网格技术，以石太专线上的太行山隧道的部分参数作为模拟时的设定参数进行了活塞风特性变化影响参数的相关研究。滑移网格技术须划分出运动域和静止域，对滑动的接触面还有网格节点分布的要求，动网格则依赖于UDF 编程，对网格质量的要求较高，但更符合流体运动的实际状态。动网格技术与滑移网格技术对研究流场的瞬态特性均体现出一定的有效性，目前虽有关于两种方法的对比研究[16,17]，但针对隧道活塞风的对比研究却几乎没有。本文针对列车在隧道中运行产生活塞风的过程，尝试采用数值模拟的方法，将滑移网格技术与动网格技术的模拟数据与参考文献[4]中的实测数据做对比，在验证模拟方法正确性的基础上，比较两种方法在二维情况下模拟隧道列车活塞风时的适用性及优劣性。

1 建模及模拟合理性验证

1.1 动网格

动网格技术是将列车本身看成一个整体，空气流场为另一部分，将车速以UDF 函数的形式赋予列车壁面，列车为刚体运动带动周边网格进行更新及数据交换。动网格的计算遵循守恒方程，二维情况下其通式为：

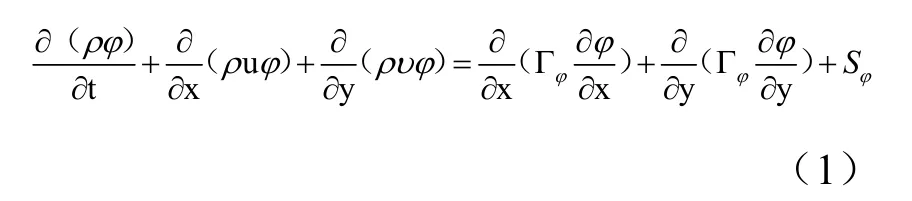
式中：ρ是流体的密度；u、v 是流体的速度矢量；Γ 是扩散系数；是通量的源项φ[18]。

1.1.1 动网格划分及设定

在动网格模型中，网格质量和参数设定都会对网格更新产生很大影响，若设置不当会导致迭代过程中网格产生负体积报错而不能完成计算。本文采用弹簧光顺（Smoothing）和局部重构（Remeshing）两种方法实现动网格的更新。局部重构法是指当网格尺寸及畸变率大于设定值时，将自动对运动边界附近区域的网格重新构建。弹簧光顺法是将网格的边界节点视为相互连接的理想化弹簧，网格节点发生位移后，原有的理想弹簧平衡状态被打破，通过不断调整最终达到新的平衡[18]。此方法适用于三角形及四面体网格模型中，在非三角形及非四面体网格模型中使用时容易引起网格变形率过大而更新失败。

图1 是三角形非结构化网格划分的示意图。根据上述，本文选用三角形非结构化网格进行动网格计算，并对列车壁面附近的网格进行加密。计算时运动的列车壁面将带动附近区域的网格更新，列车前方网格受到挤压，列车后侧网格受到拉伸，当拉升超过限制时网格将自动重新组合。

图1 三角形非结构化网格划分示意图Fig.1 Schematic Diagram of Triangular Unstructured Mesh Partition

1.1.2 动网格独立性验证

本文选取三组不同数量、不同密度的非结构化网格进行活塞风速的模拟，网格数及节点数如表1所示。

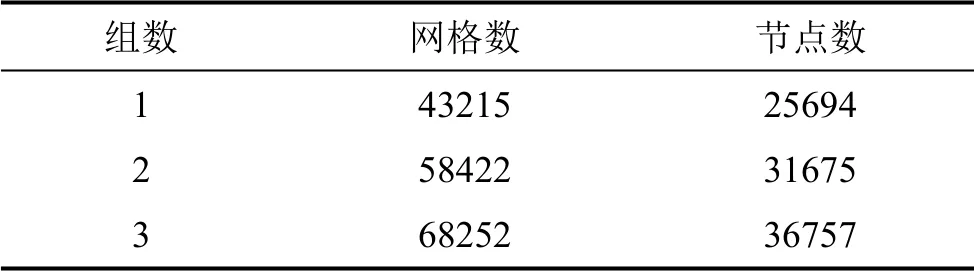
表1 网格独立性验证取值表Table 1 Grid independence validation value table

选取车体经过监测面阶段的风速平均值进行比较，整理成点线图如图2所示。从图中可见，5.8万网格数模拟出的平均风速与6.8 万网格数模拟出的平均风速相差不大且与实测平均值差别较小，此时的网格密度已经足够保证计算精度，故可以用作整个隧道活塞风的模拟。

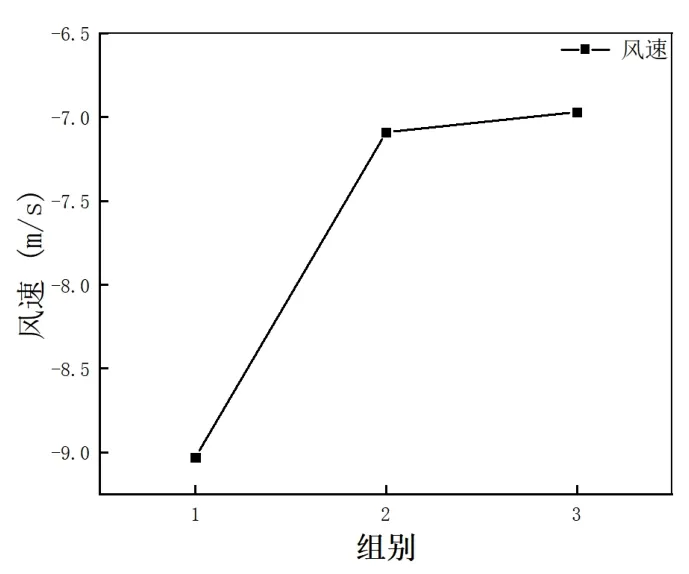
图2 平均风速随网格数变化图Fig.2 Variation of average wind speed with grid number

1.2 滑移网格

滑移网格在建模时较动网格复杂得多，它不需要网格进行形变或重构，而是通过不同滑移网格区域接触面间互相信息传递进行计算，因此在建模时需要将模型划分为含有列车的运动网格区域和相对静止区域，两者通过滑移网格交界面（interface）进行接触。迭代过程中由profile 文件或UDF 文件指定滑动区域按一定的方向进行整体移动。技术原理图如图3所示。

图3 滑移网格信息交换示意图Fig.3 Schematic diagram of sliding grid information exchange

图中，交界面区域由A-B 面、B-C 面、C-D 面及E-F 面、F-G 面和G-H 面组成，交叉处产生a-b面、b-c 面和c-d 面等。在两个单元区域重叠处产生b-c 面、c-d 面、d-e 面、e-f 面、f-g 面，剩余的a-b 面和g-h 面成对形成周期性区域。在图中，若计算分界面流入2 单元的流量，则用d-e 面和e-f面代替B-C 面从而进行信息传递。

1.2.1 滑移网格划分及设定

本文依然采用patchway 隧道的相关数据[4]进行滑移网格的计算，采用四边形结构化网格。列车从距离隧道入口35m 处出发，为简化计算，将列车及周围网格定义为刚体运动，网格划分较为密集；列车前后区域属于变形区域，网格划分应稀疏一些；由于隧道壁附近区域在计算时需采用壁面函数法，网格划分也应密集一些；其他远场区域用来模拟列车进隧道前的外界环境，对计算影响不大，网格划分较为稀疏。具体如图4所示。

图4 四边形结构化网格划分示意图Fig.4 Schematic Diagram of Quadrilateral Structured Grid Division

1.2.2 网格独立性验证

本文分别选取总数为23 万、27 万和31 万的三组网格进行模拟，图5 对比了车体经过监测面阶段的风速平均值。从图中可见，27 万网格数模拟出的平均风速与31 万网格数模拟出的平均风速基本一致，故此时的网格密度已经足够保证计算精度。研究中为便于计算、节省计算时间，选取27万网格的模型作为整个隧道活塞风的模拟。

图5 平均风速随网格数变化图Fig.5 Variation of average wind speed with grid number

1.3 数值方法

非稳态流场的模拟两种方法均采用CFD 软件fluent 完成，计算时采用双精度的隐性分离算法器进行计算，压力和速度耦合运用PISO 算法，动量项、湍流动能项、湍流扩散项都采用QUICK 格式。各变量的松弛因子取0.7～1.0，其他压力松弛因子为0.3～0.4。处理边界条件时本文将隧道入口和出口均设置为压力进、出口，将隧道壁面设置为常壁温，隧道和列车的当量粗糙高度分别为5mm、9.2mm。湍流模型采用RNGk-ε双方程模型，时间步长为最小网格尺寸与列车最大运动速度的比值，取0.008s。

2 模拟计算及对比分析

隧道内的列车都呈现出细长的特性，当列车高速通过隧道时，会引起隧道中的流场发生复杂变化。由于隧道壁面的限制，隧道内的空气部分被车挤压而绕流到列车后方，部分被列车推动顺着列车行驶方向流动，近似于做活塞运动。为方便模拟，在建模时对实际情况做出以下简化：

（1）将隧道和列车均简化为长方形；

（2）忽略隧道内部围护结构及辅助设施对流场研究的影响，忽略车表面门把手、车灯等凸起物；

（3）不考虑隧道截面尺寸及轨道坡度的变化且认为列车做匀速运动；

（4）将隧道内部空气视为理想气体，隧道内部流体视为不可压缩流体。

本文首先采用动网格方法来验证数值模拟的有效性，建模的参数参考有实测数据的英国Patchway 隧道[6]，具体数据如表2所示。

表2 Patchway 隧道及列车基本参数Table 2 Basic parameters of the Patchway tunnel and train

2.1 隧道列车活塞风速模拟计算及对比分析

本次模拟设定列车运行速度为与实际运行速度一致的35m/s，监测面设置于距离隧道入口150m处。计算出动网格技术与滑移网格技术分别在列车车头未到达测点、列车车身经过测点、列车车尾过测点后三个阶段的活塞风速平均值，并与实测值[6]进行比较，如表3所示。

表3 活塞风速平均值对比Table 3 Comparison of mean piston wind speed

对比表中数据可以看出：

（1）整体三个阶段动网格技术模拟出的数据平均值均较滑移网格偏差率小；

（2）滑移网格技术与动网格技术均在计算第二阶段时产生较一、二阶段大的偏差。这一阶段为车身经过监测面阶段，此时空气流通截面急剧减小，环隙空间的空气受到列车壁面及隧道面的双重阻碍，运动方向复杂变化，故模拟数据可能产生较大波动，与实际情况相符；

（3）比较一、三阶段数据可以看出，滑移网格技术与动网格技术均在计算第一阶段时产生比第三阶段相对更大的偏差，这是因为第一阶段列车车头刚进入隧道运行，此时活塞风还处于发展阶段，不太稳定；第三阶段列车已在隧道内运行了较长一段距离，此时活塞风发展的较为稳定。因此上述差异符合活塞风的发展规律。

将实测数据与动网格和滑移网格模拟出的数据整理成折线图绘制如图6所示。

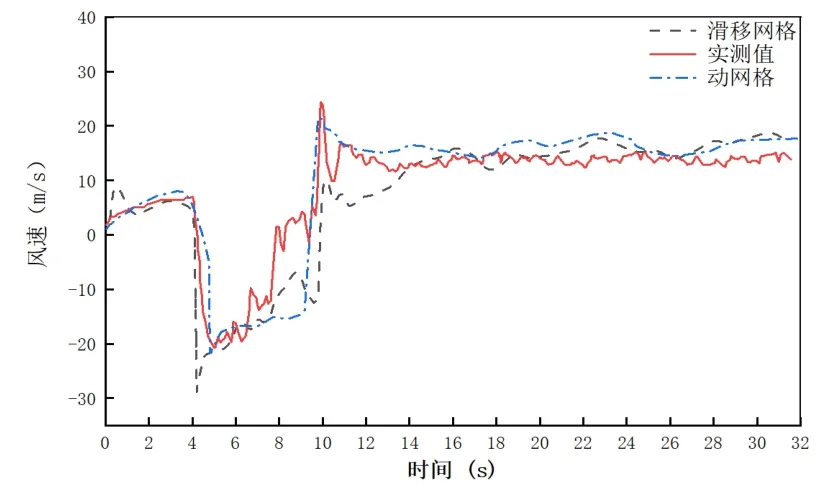
图6 不同方法计算隧道活塞风速的比较Fig.6 Comparison of tunnel piston wind speed calculated by different methods

观察图6 可以得出以下结论：

（1）滑移网格与动网格在模拟过程中活塞风的变化趋势与实测时的变化趋势基本一致，这验证了模拟方法的正确性，即两种方法均适用于模拟隧道活塞风；

（2）两种模拟方法的曲线均较实测数据平滑，这是因为模拟过程中忽略了隧道及列车表面一些附属设施对活塞风的影响，且实测是在隧道截面上的一个点进行监测，而模拟是选取二维模型中一个面进行监测，因此上述差异存在一定合理性。

2.2 隧道列车压力云图对比及分析

图7 是两种技术在模拟列车运行到隧道内210m 处时车头、车尾部位的压力云图。其中（a）（c）是动网格，（b）（d）是滑移网格。

图7 动网格和滑移网格压力场对比Fig.7 Pressure field comparison between moving mesh and sliding mesh

两种方式下列车均运行到相同位置，故具有一定的参照性。对比得出两种方法模拟出的趋势一致，均在车头处表现出正压，车尾处表现出负压。但动网格对于列车在隧道中运行的描述较为准确，可以看到动网格车头处压力变化对称均匀且发展完全，车头顶端及底端表现出较小范围的负压区域，最大正压的边界区域较滑移网格小。而滑移网格车头处压力在滑移面处有明显的小范围波动，压力发展速度较动网格快。动网格模拟出的车尾部分压力发展较为均匀，而滑移网格可以看出明显的负压的尾涡区域。此外，根据2.2 的分析，环隙区域应为活塞风变化最剧烈的部分，在动网格压力云图中可以观察到压力复杂变化的痕迹，而滑移网格在环隙部分的压力却均匀变化。

3 结论

本文以有实测数据的隧道为数据模型，应用动网格技术与滑移网格技术分别对隧道进行了动态模拟，对比得到以下结论：

（1）就活塞风速而言，动网格与滑移网格模拟出的变化趋势均与实测数据基本一致，但均值动网格的偏差率更小，两者偏差率在车身经过测点阶段时相差最大，达29%。

（2）就压力变化而言，动网格与滑移网格对于列车在隧道中压力变化过程的模拟趋势一致，但动网格能较好的还原这一过程，更符合隧道活塞风发展的理论研究。

（3）在模拟隧道活塞风时，动网格建模的计算思路与我们对实际问题的理解一致，而滑移网格需要对模型进行转化，建立滑移面并适当扩大计算区域，且滑移网格法在滑移面处有较小波动。