基于核熵成分分析的综合干旱指数的构建与应用—以黑河流域中上游为例

郭盛明，粟晓玲,2，吴海江，姜田亮，梁 筝，冯 凯

(1.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；2. 西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

旱灾发生频率高、影响范围广、灾害损失大，被认为是世界上最严重的自然灾害之一[1-2]。随着全球气候变化和社会经济的高速发展，人类对自然环境的干预越来越大，降低了气候系统的稳定性，加速了降水、蒸发等水循环过程，使得洪旱灾害的发生风险进一步增大[3-4]。

干旱通常被分为气象干旱、农业干旱、水文干旱、社会经济干旱4种类型。常用影响干旱的气象、水文要素构建干旱指数监测干旱。气象干旱是指降水量与蒸发量之间长时间不平衡而出现的水分短缺现象[5]，常用帕尔默干旱指数(Palmer drought severity index，PDSI)、标准化降水指数(Standardized precipitation index，SPI)、标准化降水蒸散发指数(Standardized precipitation evapotranspiration index，SPEI)等表征[6]。农业干旱主要指土壤水分在一段时间内持续亏缺造成农作物不能正常生长发育的现象[7]，常用K指数、降水距平百分率、标准化土壤湿度指数(Standardized soil moisture index，SSMI)等表征[8]。水文干旱是指河川径流满足不了供水需求，使得可利用水量低于正常水平的现象[9]，常用径流距平指数、地表供水指数、标准径流指数(Standardized runoff index，SRI)等表征[10]。

干旱的发展及传递过程复杂，使用单变量干旱指数无法描述干旱的全部特征，因此，需要探究一种融合多变量的方法来构建综合干旱指数[11]。常用的构建方法主要有水量平衡法、权重法和概率统计法[12]。其中，权重法包括熵权法、主成分分析法(PCA)等。王玺圳等[13]采用客观赋权法联合SPEI、NDVI、SSI和SGI构建综合干旱指数CDI；Wang 等[14]基于PCA考虑了径流变化提出了一种新的标准化降水蒸散径流指数SPERI。概率统计法常用Copula函数，Hao等[15]基于Copula 函数联合SSI和SPI提出了多变量标准化干旱指数MSDI；张迎等[16]采用Copula 函数联合SPI和SRI构建综合干旱指数MSDIp。熵权法、PCA等方法将若干变量线性组合在一起，可有效提取特征间的线性关系，但不能很好地反映变量间的非线性关系。Copula函数能连接多个不同分布的变量，但计算方法繁杂，尤其是连接3个及以上变量时。核熵成分分析(Kernel entropy component analysis，KECA)是对PCA的深层次改进，其在特征空间进行熵成分分析以实现数据变换，具有良好的非线性处理能力且计算相对简单[17]。目前，KECA已被广泛应用于目标分类、故障检测等领域[18-20]，但在干旱领域鲜有应用。本文基于SPEI、SSMI和SRI，采用KECA构建综合干旱指数SMDI，并探讨其时空演变特征和适用性，以期为干旱监测提供科学指导。

1 研究区概况和数据来源

1.1 研究区概况

黑河是我国第二大内陆河，位于河西走廊中部，东以山丹县境内的大黄山为源，西以嘉峪关境内的黑山为界，地理坐标为97°50′～102°00′E，37°50′～42°40′N[21]。黑河干流发源于祁连山系的走廊南山和冷龙岭，全长821km，由莺落峡和正义峡两断面将其划分为上、中、下游。上游为主要产流区，植被较好，为牧业区；中游为径流利用区，也是重要农业区，主要依靠黑河供水，干旱缺水；下游植被稀少，为径流消耗区[22]。

1.2 数据来源

气象数据为黑河流域中上游12个气象站1966—2016年逐月降水、风速等气象资料，来源于中国气象科学数据共享服务网(http://data.cma.cn/)。水文数据为黑河干流莺落峡和正义峡两个水文站1966—2016年的逐月径流资料，来源于国家自然科学基金委员会“黑河数据计划管理中心”。黑河流域中上游1966—2016年逐月土壤湿度数据来源于全球陆地数据同化系统(GLDAS)数据集，空间分辨率为0.25°×0.25°。通过ArcGIS将土壤湿度数据重采样为0.125°×0.125°栅格数据集，与气象、水文联合进行黑河流域中上游栅格计算。流域气象站及水文站分布见图1。

2 研究方法

2.1 单变量干旱指数的研究方法

用SPEI、SSMI和SRI3种指数分别表征气象干旱、农业干旱和水文干旱。SPEI的计算方法详见文献[23]，其中潜在蒸散发量(ET0)采用Penman-Monteith公式计算[24]。

土壤湿度的边缘累积概率P(xi)使用非参数的Gringorten[25]经验位置划分公式来计算，公式如下：

P(xi)=(i-0.44)/(n+0.12)

(1)

式中，i为土壤湿度序列升序时的次序，n为样本序列长度。

将经验累积概率P(xi)进行逆标准化即得到非参数化的SSMI，公式如下：

SSMI=φ-1(P)

(2)

式中,φ为标准正态分布函数，P为经验累积概率。

SRI的计算方法与SPI类似，但与SPI假定降水服从Gamma分布不同，SRI假定径流服从对数正态分布。在求得径流的累积概率之后将其逆标准化即得到SRI。

2.2 核熵成分分析(KECA)基本原理

KECA通过构造数据的Renyi熵，以高维特征空间能最大程度保持原始空间Renyi熵的坐标轴为投影方向[26]。

给定N维样本x，其概率密度函数为p(x)，则p(x)的Renyi 熵可表示为：

(3)

由于对数函数具有单调性，所以只需关注真数部分，真数部分用V(p)表示：

(4)

引入Parzen窗函数估计V(p)值，表达式如下：

(5)

式中，K(xi,xi)为Parzen窗函数(核函数)，xi为中心，为宽度参数。

可以获得V(p)的估计值：

(6)

式中，K是一个N阶的核矩阵，K(i,j)=K(xj,xi)；I是一个N×1向量(向量中的每个元素均为1)。

样本集的Renyi熵可通过核函数进行估计。将核矩阵K进行特征值分解：K=EDET，其中D=diag(λ1,λ2,…，λN)是特征值所构成的对角线矩阵，E=[α1,α2,…,αN]是由相应的特征向量组成的特征矩阵，λ和α为Renyi熵的估计值按降序排列后的特征值和特征向量。将D和E代入式(6)可得到Renyi熵值V(p)，表达式如下：

(7)

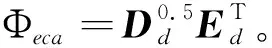
(8)

目前常用的核函数包括径向基(Radial basis function, RBF) 核函数、多项式核函数、感知器核函数等。其中RBF核函数应用广泛且具有良好的适用性[27]，本研究选用RBF核函数，表达式为：

(9)

式中,k(xi,xj)为核矩阵元素；θ为宽度参数；‖· ‖为2范数。

θ的选取原则是使用较少的主成分来达到显著的降维效果，即使得ξ值较大。通过比较不同的参数进行择优，这里θ取值范围为0～5。基于KECA将3种单变量干旱指数联合后，即可得到综合干旱指数MDI。

2.3 标准化综合干旱指数SMDI计算方法

为与SPEI、SSMI及SRI比较，对MDI标准化处理。选取正态、对数正态、Weibull、Gamma及Logistic 5种具有较强适用性的理论函数拟合MDI序列，选取极大似然法估计分布函数参数，采用K-S检验进行拟合优度检验，并用AIC准则进行最优拟合函数选择，之后将所得累积概率逆标准化，得到标准化综合干旱指数SMDI。若5种分布都不满足精度要求，则选择非参数法计算SMDI。

本研究的干旱等级划分参考SPI的统一标准(表1)。

表1 干旱指数等级划分Table 1 Drought severity grades and their corresponding D-scale

2.3.1 K-S检验法 K-S检验是一种拟合优度检验法，用于判别样本是否服从假定的理论分布。比较样本的累积分布曲线与假设的理论频率曲线并计算两者的差值，若差值的绝对值在规定范围内，表明该样本服从假设分布。

以H0、H1分别表示样本序列服从理论分布和不服从理论分布，构造统计量D：

D=max|F1(x)-F2(x)|

(10)

式中，F1(x)表示样本累积分布概率，F2(x)表示理论分布概率。

选定显著性水平α=0.05，当D>D(n,α)时，接受H1，否则接受H0。

2.3.2AIC准则AIC准则是一种常用的最优拟合函数选择方法，能找出适配数据最优且自由参数个数较少的模型。AIC值越小，拟合效果就越好[29]。

AIC=2k-lnL

(11)

式中,k为模型自由参数个数，L为拟合的极大似然函数。

2.4 Mann-Kendall(M-K)趋势检验法

M-K趋势检验是一种分析时间序列趋势的非参数检验方法，具有检测范围广、定量化程度高等优点[30]。公式如下：

(12)

式中,S为构造的统计量；n为样本序列长度；xj和xi是第j年和第i年对应数值。两者之差大于0时，sgn值为1，小于0时sgn值为-1，等于0时sgn值为0。

当n大于8时服从正态分布，均值E(S)为0，方差Var(S)通过下式求得。

Var(S)=n(n-1)(2n+5)/18

(13)

构造标准化的检验统计量ZMK:

(14)

检验统计量ZMK无量纲单位，当ZMK的值为正(负)时，表示样本序列随时间的增加有增大(减少)的趋势。当|ZMK|大于1.96时，认为在α=0.05的显著性水平下变化趋势明显，反之则不明显。

2.5 小波周期分析

小波方差图可以确定一个序列中各种时间尺度相对扰动强度的大小，进而反映样本序列的主要周期[31]。在经济学、水文学等诸多需要分析时间序列周期性的领域被广泛应用[32]。计算公式如下：

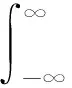
(15)

式中，Wf(a)为小波方差，a为尺度因子，b为平移因子，Wf(a,b)为小波系数。

3 结果与分析

当核函数的宽度参数θ为2时，黑河流域中上游各栅格第一主成分的累积贡献率ξ>99%，所以取参数θ为2。本研究选取季时间尺度(3个月，即3—5月为春季，6—8月为夏季，9—11月为秋季，12月—次年2月为冬季)来分析黑河流域中上游干旱指数四季的趋势变化、年代变化、周期变化和干旱发生频率变化，并与历史旱情事件比较以分析SMDI的适用性。

3.1 不同季节干旱指数序列分析

用黑河流域中、上游各栅格的不同干旱指数均值来表征中、上游的干旱状况，并按季节分别比较各干旱指数间的差异(图2～图3)。

由图2、图3可知，同时考虑气象、农业、水文3种要素的综合干旱指数SMDI与分别只反映气象干旱、农业干旱、水文干旱的单变量干旱指数SPEI、SSMI及SRI的年际变化不同，且在不同季节各干旱指数值亦有较大差异。单变量干旱指数值在同一时段有时相差很大，而综合3种变量的标准化综合干旱指数SMDI则在3者之间波动变化。在有些年份SMDI和3种单变量干旱指数值趋势相反，这是因为3种单变量干旱指数都是按照同一分布计算得到。而SMDI则是使用5种参数分布和一种非参数法进行优选得到，各个栅格的分布类型不尽相同，这样可在黑河流域中上游空间分布上达到最优。但由于不同栅格SMDI有正有负，在取栅格平均值时会抹去一些信息，从而表现为SMDI值偏大或偏小。2005年以后，SMDI值整体要比其他3种单变量干旱指数值偏小，说明近年来黑河流域中上游的干旱程度有所加剧。

3.2 干旱趋势演变分析

分析黑河流域中上游4种不同干旱指数的四季变化趋势(图4)，根据干旱加重或减轻及变化是否显著将其分为4类，分别用干旱显著加重(T1)、干旱不显著加重(T2)、干旱不显著减轻(T3)、干旱显著减轻(T4)来表示。

由图4可知，气象干旱除上游部分区域在夏、秋两季干旱不显著减轻，流域整体呈现干旱加重趋势，且春、冬两季尤为显著；农业干旱除中游边界地区有部分区域干旱加重，整体呈现干旱减轻趋势；水文干旱上游表现为干旱显著减轻趋势，中游在夏、秋两季有干旱不显著减轻趋势，而春、冬两季呈现干旱不显著加重趋势。综合了气象、农业、水文的SMDI在趋势演变上与气象干旱相近，但变化趋势不显著，除秋季中游部分区域有干旱显著加重趋势，其他区域在四季变化上整体呈现干旱不显著加重趋势。统计流域干旱不显著加重趋势的格点占比，春季85.8%，夏季62.9%，秋季80.2%，冬季80.5%，全年77.6%，所以流域有77.6%的区域呈现干旱不显著加重趋势。

考虑SPEI是由降水与潜在蒸散发的差值序列拟合分布得到，分析黑河流域中上游12个气象站四季降水和潜在蒸散发趋势变化见表2。

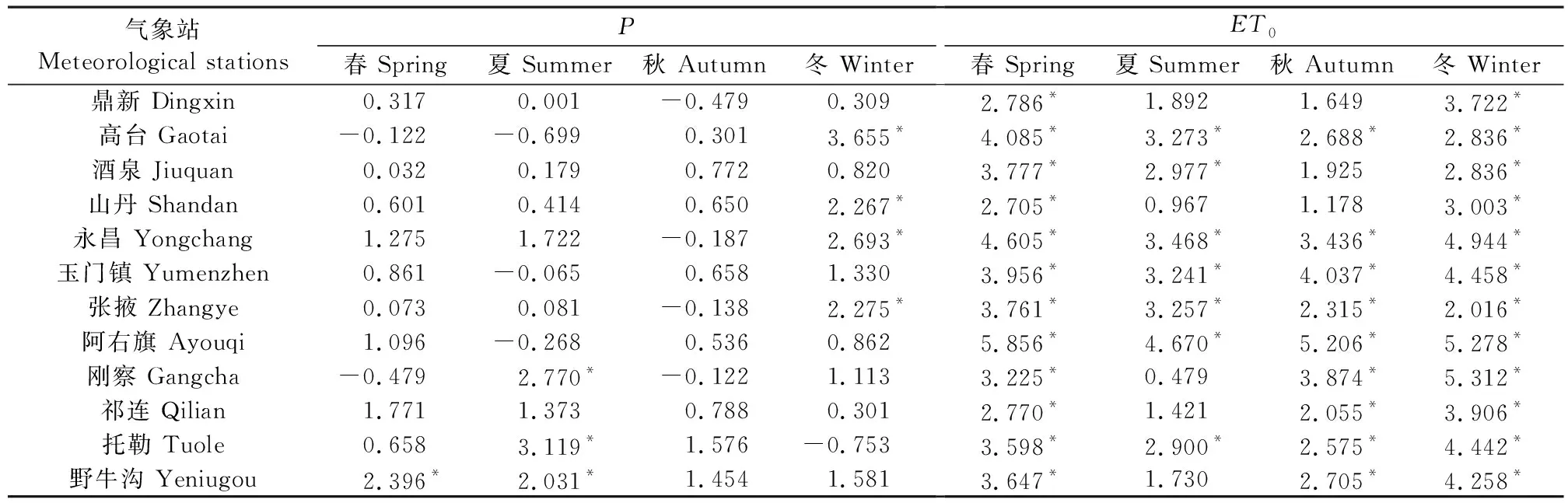
表2 黑河流域中上游四季降水量(P)、潜在蒸散发量(ET0)趋势变化Table 2 The tendency change of precipitation (P) and potential evapotran spiration (ET0)in the upper and middle Heihe River Basin

由表2可以看出，12个气象站在51年中，除个别站点在某些季节降水有不显著减小趋势外，整体呈现增大趋势，这与陈洁等[33]发现的近年来西北地区降水增多相符，但增多趋势不显著。而流域所有站点的潜在蒸散发量在各季节都呈增大趋势，且多数站点都呈显著增大趋势。降水量的增加使得径流量增多，表现为水文干旱逐渐减弱。但是降水量的增大不能完全抵消潜在蒸散发量的增大，因此气象干旱表现为在流域大部分地区仍然加重。全球气温升高导致蒸散发量增大，同时也加速了冰雪融水，使得径流量增多，表现为水文干旱逐渐减轻。由于近年来灌溉技术的不断发展且抽取地下水进行农业灌溉，农业干旱有减轻趋势。根据趋势演变结果可见，单变量干旱指数在反映干旱变化趋势时表征结果不相同。而SMDI则兼顾了气象、农业、水文三者的特征，是对干旱状况的全面反映，其趋势变化结果表明黑河流域中上游整体仍呈干旱加重趋势。

3.3 干旱年代变化分析

统计不同年代干旱的发生频率，可进一步比较不同年代旱情的严重程度。本文研究序列为1966—2016年，由于1966—1969年只有4 a的数据，将其合并于20世纪70年代。将研究序列分为4段：1966—1979年、1980—1989年、1990—1999年、2000—2016年，代表20世纪70年代、20世纪80年代、20世纪90年代、21世纪初，统计得到黑河流域中上游SMDI在这4个不同时期的干旱发生频率(图5)。

由图5可知黑河流域中上游在1980s旱情最轻，干旱发生频率在季节尺度上均低于30%，其次是1970s，仅黑河流域上游在春季干旱的发生频率较高。而1990s以及21世纪初流域旱情相对严重，同时这两个时期在不同季节干旱的发生频率又有所不同，1990s表现为夏、秋两季干旱的发生频率高，这与该时期黑河流域中上游城市化进程及工业发展迅速使得耗水量急剧增加进而导致严重水文干旱相符。而21世纪初则是在春、冬两季干旱的发生频率高。这是因为自2000年起黑河流域实施分水政策[34]等一系列积极举措，使得夏、秋两季干旱发生频率降低。但春、冬两季本身降水少，所以在21世纪初表现为春、冬两季干旱发生频率较高。

3.4 干旱空间特征分析

将干旱分为轻中旱和重特旱两类(表1)，对SMDI统计得到黑河流域中上游不同季节干旱的发生频率(图6)。

由图6可知，四季中，重特旱的发生频率均比轻中旱低，表明黑河流域中上游极端干旱事件的发生频率较低。其中春、夏两季轻中旱的发生频率要高于秋、冬两季，夏季轻中旱的发生频率最高。而重特旱的发生频率则表现为夏、秋两季高于春、冬两季，秋季重特旱的发生频率最高。整体来看，黑河流域中上游在夏季干旱的发生频率最高，中游干旱的发生频率整体上要高于上游。中游为流域重要的农业区，需要重点关注中游地区防旱减灾工作。

3.5 干旱周期变化分析

采用小波函数对黑河流域中上游SMDI序列做周期分析，得到SMDI的小波方差图(图7、8)。

小波方差图峰值显示对应主要时间尺度，根据图7、8将峰值从高到低排，可以得到黑河流域中上游SMDI四季主周期值(表3)。

由表3可知，黑河流域上游和中游的主周期在四季较为接近，但是在排序上略有区别。黑河流域中上游周期集中表现为43 a的长周期，15～23 a的中周期以及3～8 a的短周期。这与钟锋等[35]研究的黑河流域干旱存在19～23 a和14～15 a的中长振荡周期及7～10 a和4～5 a的短振荡周期结论基本一致。同时与太阳黑子活动周期约22 a、厄尔尼诺事件周期2～6 a相对应[36]，这表明黑河流域干旱的周期变化可能是太阳黑子活动及厄尔尼诺事件的综合驱动结果。其中仅上游春季第一主周期为43 a的长周期，其余阶段第一主周期皆为中周期和短周期，这与黑河流域中上游干旱发生频繁相对应。根据周期情况可预测未来干旱大致出现时间。

表3 黑河流域中上游SMDI四季主周期值Table 3 The main cycle values of SMDI in four seasons in the upper and middle Heihe River Basin

3.6 典型干旱事件验证

黑河流域中上游在行政划分上属于青海和甘肃两省。根据《中国气象灾害大典》[37-38]：青海卷和甘肃卷，青海、甘肃两省水资源公报以及中国水旱灾害公报记录：1969年甘肃全省大部分地区旱灾严重，春夏连旱，重旱灾涉及16县，同年青海省海南、海西州发生严重干旱；1997年甘肃全省均发生不同程度的干旱，是近60年来干旱范围最大、旱情最重的一年，同年青海省的祁连、野牛沟地区旱灾严重；2009年冬季西北大部区域发生干旱。

为进一步展现SMDI的干旱监测能力，选取1969年春、1997年秋和2009年冬与同时期的其他3种单变量干旱指数干旱监测情况进行比较(图9)。

由图9可知，1969年春，SPEI与SRI的指数值表现为无旱，与旱情记录的实际情况不符，而SMDI的监测结果与SSMI相近，都可以监测到较大区域的干旱。1997年秋4种干旱指数值在流域大部分区域均表现为发生干旱，但SPEI的监测结果在部分区域表现为无旱。而SMDI和SSMI及SRI识别区域基本一致，但在红框所示区域不同，此区域SMDI值比3种单变量干旱指数小，即SMDI所表征的干旱等级高于3种单变量干旱指数所表征的干旱等级。历史旱情记录1997年秋是近60年来旱情最严重的一年，可以看出SMDI与本年旱情更为相符。2009年冬，西北地区大部区域发生干旱，但SRI和SSMI在黑河流域中上游表现为无旱，而SPEI识别出的发生干旱的流域面积没有SMDI识别出来的大。与以熵权法联合SPEI及SSI构建的气象农业综合干旱指数AMDI[39]相比，AMDI在旱情验证上不能很好反映气象和农业之间的非线性关系，表现为在春旱验证上与历史旱情事件没有较好对应。而基于KECA构建的SMDI则能够反映不同类型干旱之间的非线性关系，旱情验证结果优于AMDI，体现了KECA在反映不同变量间非线性关系上具有优越性。说明SMDI比单变量干旱指数及熵权法构造的AMDI在黑河流域中上游的干旱监测适用性更好。

4 结 论

本文以黑河流域中上游为研究区，使用新的降维方法KECA联合了气象、农业、水文3种变量来构建综合干旱指数SMDI，并对黑河流域中上游干旱的时空特征进行分析，同时与典型历史旱情事件作验证比较，主要得到以下结论：

1)黑河流域中上游除部分区域表现为干旱不显著减轻外，整体仍表现为干旱加重趋势，且有些区域加重趋势显著；在20世纪90年代夏、秋两季和进入21世纪以来春、冬两季旱情最为严重；干旱存在43 a的长周期，15～23 a的中周期以及3～8 a的短周期。

2)四季中，重特旱的发生频率均比轻中旱的小，且干旱的发生频率在上游低于中游，综合来看，夏季干旱的发生频率最高。

3)历史典型旱情验证结果表明，基于KECA构建的SMDI在干旱的捕获区域以及极端干旱事件的反映上优于其他3种单变量干旱指数及熵权法构建的综合干旱指数，能够反映多种干旱变量之间的非线性关系，在黑河流域中上游干旱监测中有着更好的适用性。

在气候变化与人类活动影响更剧烈的大环境下，气象、农业、水文3种干旱之间的关系更为复杂，传统的单变量干旱指数难以全面表征干旱的综合特征，综合干旱指数的发展与应用，能够弥补传统单变量干旱指数的不足，为决策者提供有益参考。本文使用KECA构建的SMDI，可表征气象、农业和水文干旱之间的非线性关系，适用于黑河流域中上游干旱的监测。该方法是否存在区域性差异，在其他区域是否适用，需作进一步验证。