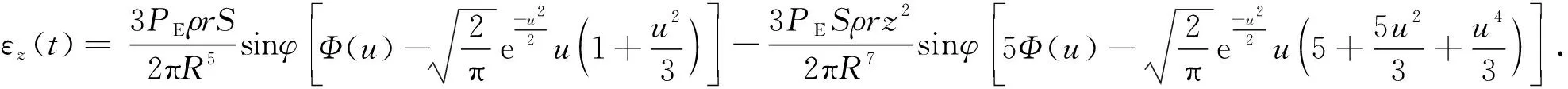地-空瞬变电磁法电阻率成像研究与应用

马振军， 底青云*， 薛国强， 高雅

1 中国科学院深地资源装备技术工程实验室, 中国科学院地质与地球物理研究所, 北京 100029 2 中国科学院页岩气与地质工程重点实验室, 中国科学院地质与地球物理研究所, 北京 100029 3 中国科学院地球科学研究院, 北京 100029 4 中国科学院大学, 北京 100049 5 中国科学院矿产资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029

0 引言

随着矿产资源的供需矛盾日进突出以及矿山开采后环境问题日益严重，亟需一种适应沼泽、山区等复杂地形的探测方法.电性地-空瞬变电磁法(Semi-airborne transient electromagnetic, SATEM)是一种利用飞行平台搭载磁探头进行观测的高效、快速、高精度电磁方法.相较于航空电磁法，铺设于地面的发射源能够带来信噪比更高的信号，探测深度大，采集方式更加简便(Smith et al., 2001; Ma and Di, 2019; 李貅等, 2015; 底青云等，2019).

地-空电磁法最早出现于20世纪70年代的俄罗斯和西欧等地，并在沿海水文地质调查(Ito et al., 2011)、火山结构调查(Mogi et al., 2009; Ito et al., 2014; Allah et al., 2014; Allah and Mogi, 2016)、矿产资源探测(Meyer et al., 2016)、煤炭采空区勘查(Xue et al., 2018; Ma et al., 2020)中进行了广泛应用.融合深部和浅部的多尺度地质-地球物理信息，解译了深部结构(Di et al., 2021).然而，SATEM的发展势必对瞬变电磁法的传统成像解释带来改变，电阻率成像是在地面、全航空电磁法应用最广泛的成像方法之一.该方法是利用转换算法得到视电阻率和成像深度联系在一起以实现电阻率成像(Huang and Rudd, 2008; 毛立峰, 2013; 殷长春, 2016).地-空瞬变电磁法的成像方法研究相对较少，成像方式主要在反演方法上进行研究(Smirnova et al., 2019; 嵇艳鞠, 2013; 徐江, 2014)，然而地-空方法数据量大，数据反演耗费时间长，尤其是对于大规模扫面探测任务，反演初始值难予确定，电阻率成像具有快速、有效等特点，既解决了大规模探测高精度成像问题，又能够为反演计算提供电阻率初始值.

针对基于电偶极子发射且与接收装置不在同一平面上的SATEM特点，本文提出了一种适用于SATEM，并考虑飞行高度及电性源瞬态电磁场感应电流特点的电阻率成像法.通过分析电磁场建场过程中横向和纵向感应电流的扩散规律，基于匀半空间的电性源SATEM在空中的磁场及感应电压解析表达，分别定义了视电阻率和成像深度.本文提出的电阻率成像法得到了实际验证，对推动SATEM方法应用具有重要作用.

1 地-空瞬变电磁响应空间分布特性

视电阻率是指地下电性不均匀体和地形起伏的综合反映，即视电阻率是空间上介质真电阻率的复杂加权平均(崔江伟，2015)，根据均匀大地表面测点处场值与均匀大地电阻率的关系来求解电阻率与场值的反函数，从而定义视电阻率(殷长春和朴华荣，1991).

在时间域电偶极子中，发射源在地下产生感应电流，其扩散特性决定了地面电磁场时空分布，所以对电磁场扩散特征进一步研究能够更加清楚的阐述电性源瞬变电磁场产生和运行机制，为多尺度探测深度提供物理解释，尤其是在地-航空瞬变电磁法探测中数据采集和处理提供帮助.相较于直立共轴或水平共面装置，不接地回线源仅存在“水平电流”(Liu et al., 2019)，而长导线—大地系统中的电流方向要复杂的多，同时存在水平和垂直感应电流，这也就导致了不同响应分布的复杂性.根据均匀大地电偶极子坐标示意图(图1)及朴化荣(1990)电偶极子源磁场表达式：

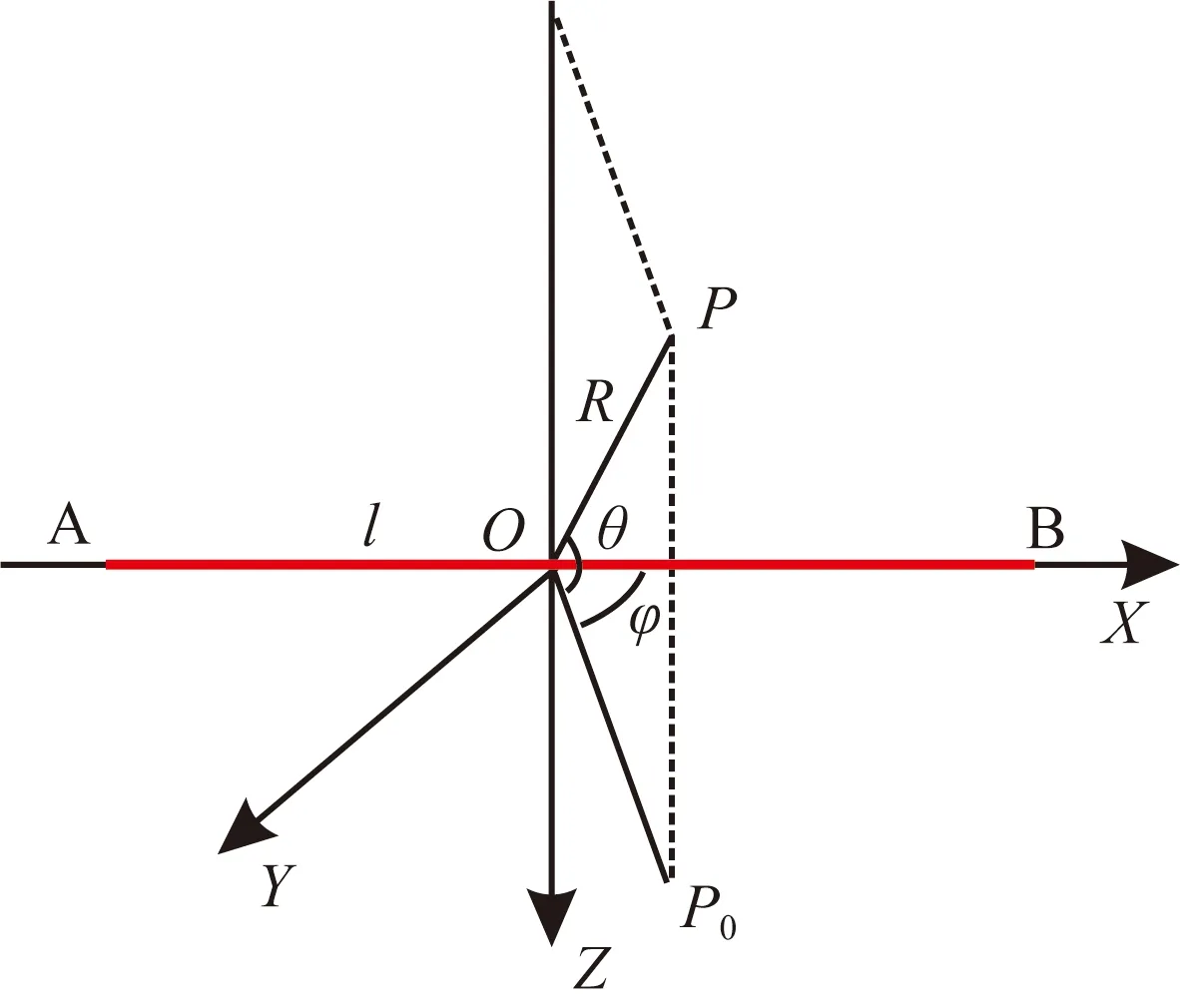
图1 均匀大地电偶极子坐标示意图Fig.1 Schematic diagram of uniform geoelectric dipole coordinates

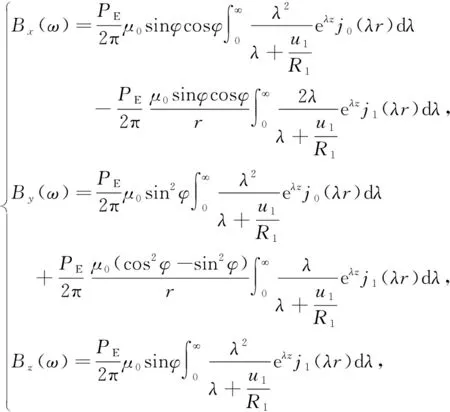
(1)

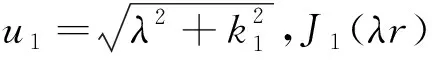
为了研究水平和垂直感应电流的分布和扩散特性，根据电流密度与电场直接的关系J=E/ρ,对电性源瞬变电磁场扩散进行可视化.本文利用公式(1)，选取200 Ωm的均匀半空间模型(如图2)计算随时间变化的电流密度分布，发射电流10A，源长1000 m.图2a、2b表示在断电1 ms,3 ms,5 ms和10 ms时在地表的感应电流平面分布，图2c、2d表示断电1 ms及10 ms在偏移距800 m处的感应电流剖面图.

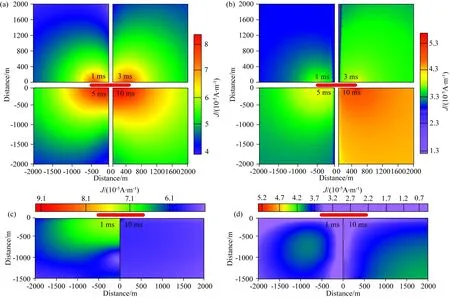
图2 电性源TEM场扩散特性(a) 地表纵向电流扩散分布; (b) 地表横向电流扩散分布; (c) 偏移距800 m时纵向电流扩散剖面分布图; (d) 偏移距800 m时横向电流扩散剖面分布图.Fig.2 TEM field diffusion characteristics(a) The distribution of longitudinal current diffusion on the earth′s surface; (b) The distribution of transverse current diffusion on the earth′s surface; (c) The distribution of longitudinal current diffusion profile when the offset is 800m; (d) The distribution of transverse current diffusion profile when the offset is 800 m.

图2表示纵向和横向感应电流的时间平面扩散特性，从图2a可以看出纵向电流首先出现在电流源附近并随时间逐渐向外扩散，电流极值逐渐向四周转移；由图2b可见，由于横向电流极值区域包括X和Y方向感应电流，主要集中在发射源正下方及发射源两侧，横向感应电流随着时间推移逐渐向外移动.图2c表示在选取偏移距为800 m时，地下感应电流及由电流引起的空中响应分布，可以看到纵向电流在均匀半空间内随时间向下移动，引起了空中横向响应(dBx/dt、dBy/dt)的幅值增强，而在图2d中，横向电流在向四周扩散时，会使得空中纵向响应(dBz/dt)减弱.

从图2可见当在均匀介质内，纵、横电流密度是连续的，但是当出现不连续的电性分界面时，电流密度会由于与电阻率界面密切相关而导致突变，形成电流密度不连续(Liu et al., 2019)，在实际应用中，利用这种现象能够精确划分电性层.

电磁场在空中的分布与扩散决定于感应电流的分布特性，对电磁场空间分布特性的研究是开展地-空瞬变电磁方法的基础.铺设于地面的电偶极源在空中可以产生dBx/dt、dBy/dt、dBz/dt三个方向的感应电压分量，虽然这三个场量都可以携带地质信息，但是每个场量由不同感应电流产生，对目标体的敏感程度，空间分布特点等出现差异.因此，我们设计200 Ωm的均匀半空间模型计算各个响应(dBx/dt、dBy/dt、dBz/dt)随时间变化的平面分布，发射电流10 A，源长1000 m，飞行高度10 m.

选取后断电1 ms,3 ms,5 ms和8 ms的各响应平面分布.如图3a，dBx/dt在平面上呈现“四瓣”状分布，最大值分布在45°线上，赤道向和轴向为0，这是由于水平磁场表达式中仅仅包含接地项，从而使得dBx/dt分别在四象限中呈现最大值，而赤道及轴线响应消失，随着时间变化dBx/dt逐渐向45°线扩散.

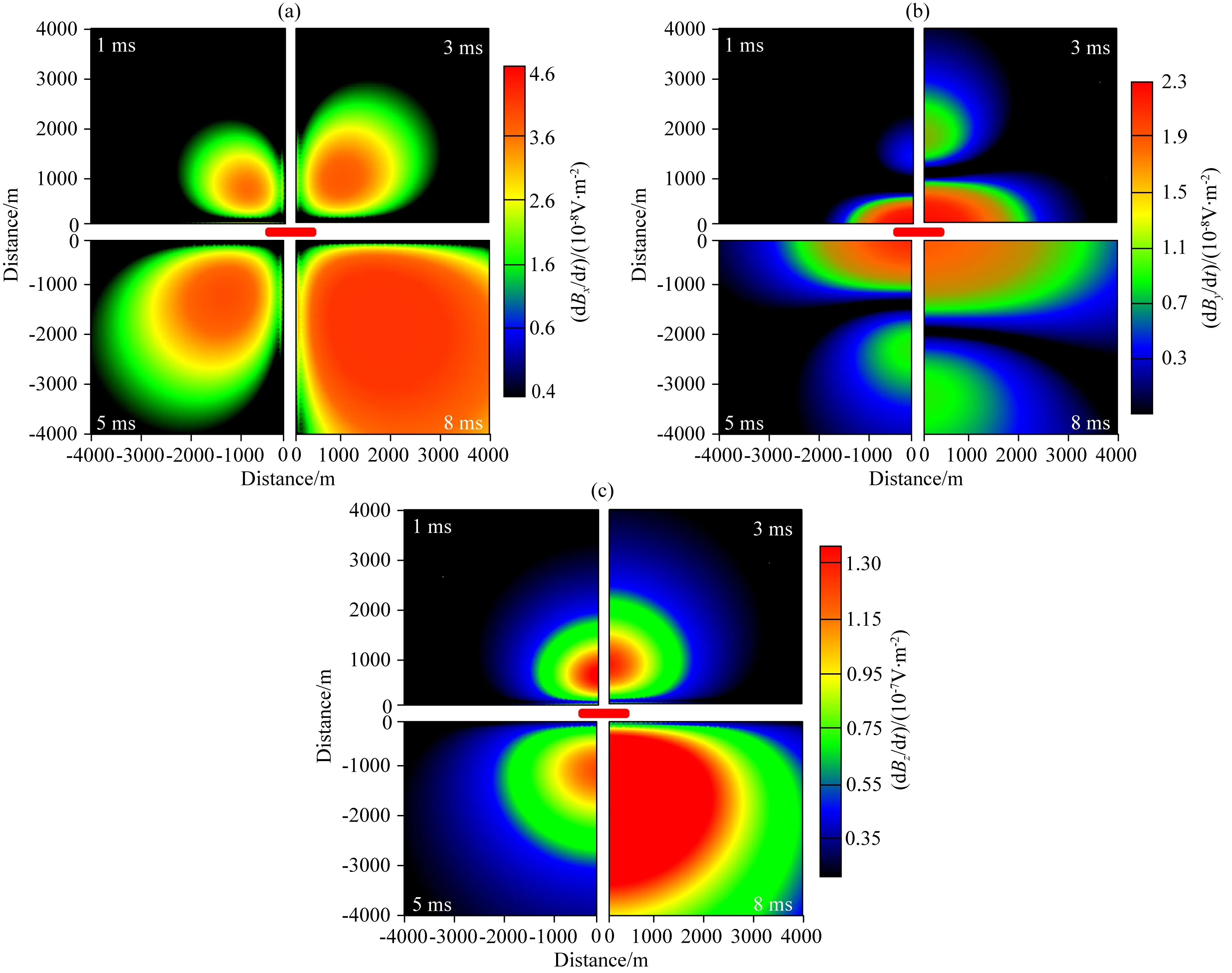
图3 电性源TEM场响应平面分布图(a) dBx/dt平面分布; (b) dBy/dt平面分布; (c) dBz/dt平面分布.Fig.3 Distribution of responses of TEM(a) Distribution of dBx/dt; (b) Distribution of dBy/dt; (c) Distribution of dBz/dt.

由图3b可知, dBy/dt在平面上呈现“三瓣”状分布，极值在发射源附近对称分布，两侧存在“次极值”，同样呈对称分布.在轴向和赤道向并没有像dBx/dt一样存在零值.我们可以把电性源感应电流分为水平感应电流和垂直感应电流，dBy/dt可以被认为由发射源所在平面的垂直感应电流和垂直感应电流感应产生，而这种垂直感应电流极值在此平面是向下扩散的(陈卫营, 2016)，所以dBy/dt的极值位置始终集中于发射源附近不会变化，“次极值”是由水平感应电流感应得来，但是符号与极值处相反.

由图3c可知，dBz/dt呈现“两瓣”状分布，其极值分布于发射源的两侧，与dBy/dt分布相同的是，在轴向上dBz/dt同样是零值，但是在赤道向上则不同.

为了研究各分量随高度变化的分布特点，偏移距设置为800 m，形成左侧为5 ms，右侧10 ms的TEM场响应剖面图(图4).如图4a所示，dBx/dt的极值存在于发射电极两侧，随着高度增加幅值降低；断电时间越久，dBx/dt幅值向上、向外扩散，高度与时间的变化没有对极值点的位置产生影响，这与平面分布、扩散相对应.如图4b所示，dBy/dt的极值点在发射源中点位置，高度的变化影响了响应幅值，并随高度升高而幅值降低；dBy/dt向四周扩散，但是极值点没有变化.如图4c所示，dBz/dt相对X和Y分量的幅值略高，但是与时间、高度的关系和其他分量相似.

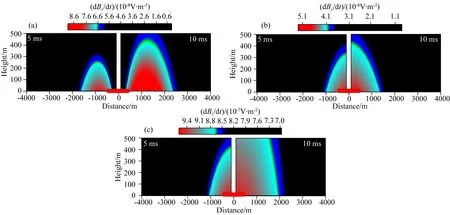
图4 电性源TEM场响应剖面图(a) dBx/dt剖面图; (b) dBy/dt剖面图; (c) dBz/dt剖面图.Fig.4 Section of responses of TEM(a) Section of dBx/dt; (b) Section of dBy/dt; (c) Section of dBz/dt.

2 视电阻率定义

飞行高度对响应强度产生影响，对实测数据进行忽略高度的传统地面视电阻率计算是不合理的.地-空瞬变电磁法电阻率成像首先要解决考虑高度视电阻率定义问题.我们根据Kaufman和Keller(1983)和底青云和王若(2008)在地面响应公式进行进一步推导，得到均匀半空间中电性源瞬变电磁场在空中响应的解析表达(推导步骤见附录)：

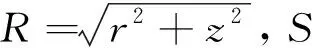
2.1 早期视电阻率

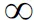
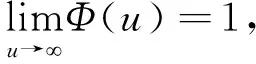
(4)

(5)

则公式(3)变为

(6)

则视电阻率为

(7)

我们设置了D、G、H、K、A、Q六种模型，飞行高度为50 m，PE=10000 Am，r=500 m，赤道向接收.黑色实线为传统基于地面公式根据单调性与二分法计算出的早期视电阻率ρearly-ground，红色实线为我们推导出的考虑飞行高度的早期视电阻率ρearly，图4下方为ρearly-ground和ρearly的相对误差.

根据G和D二层模型，τ/R<1.8时，早期视电阻率更加准确，符合真实模型，随着时间延迟，视电阻率逐渐接与真实模型误差变大以至无法反映真实电阻率.在H、K、A、Q三层模型中，ρearly-ground和ρearly对模型的反映变化相似，ρearly平行上升到ρearly-ground，所以会出现两者相对误差曲线不变的现象.利用早期视电阻率对晚期数据计算时，会出现很大误差.

设置200 Ωm的均匀半空间模型，PE=10000 Am，r=500 m，赤道向接收，选择晚期时间道时(t=0.0001 s).图5为晚期视电阻率随高度的变化曲线，红色实线为电性源地-空瞬变电磁晚期视电阻率曲线，黑色实线是基于地面感应电压公式的晚期视电阻率随高度变化曲线，柱状图为两者随高度变化的相对误差曲线.真实电阻率与飞行高度理论上讲没有联系，但是根据上图看见，利用地-空数据进行传统地面视电阻率时，会出现误差，并且误差随高度变化逐渐增大，当飞行高度从5 m变化到100 m时，早期视电阻率会降低25.6%，这极大影响了成像结果.利用考虑飞行高度的早期视电阻率进行计算时，可以得到更加准确的结果，最大变化率为2.7%，远远小于前者，而在低于50 m高度范围内，视电阻率的变化可以忽略.两种方法得到的视电阻率的相对误差随着高度的变化单调增加，最大误差为15%.

2.2 晚期视电阻率

当考虑晚期或者近区时，t→或者R很近时，考虑泰勒级数展开

(8)

(9)

令

εz(t)=εz0-Δεz(t),

(10)

εz0为地面视电阻率，Δεz(t)为地面视电阻率和空中信号计算的视电阻率之差，先求得地面视电阻率为

(11)

(12)

所以SATEM视电阻率可以为

(13)

上式中，S为接收线圈有效面积，右侧项为受高度影响后变化的视电阻率，我们利用图5中六种模型，飞行高度为50 m，PE=10000 Am，r=500 m，赤道向接收.黑色实线为传统基于地面公式推导出的晚期视电阻率ρlater-ground，红色实线为我们推导出的考虑飞行高度的晚期视电阻率ρlater，蓝色虚线为 ，图7下方为ρlater-ground和ρlater的相对误差.

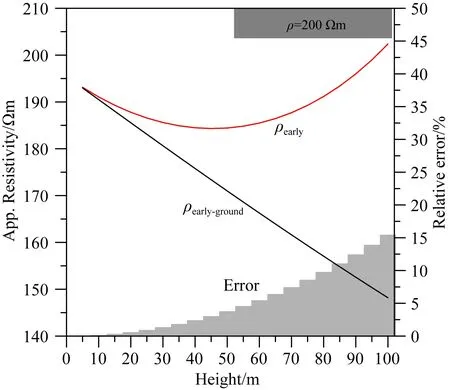
图6 早期视电阻率随高度变化图Fig.6 Early apparent resistivity changes with height

图7 晚期视电阻率典型模型计算(a) D模型; (b) G模型; (c) H模型; (d) K模型; (e) A模型; (f) Q模型.Fig.7 Typical model calculation of later apparent resistivity(a) D model; (b) G model; (c) H model; (d) K model; (E) A model; (f) Q model.

根据G和D二层模型，τ/R>4.5时，晚期视电阻率更加符合真实电阻率，随着时间延迟，视电阻率逐渐接近基底电阻率，ρlater-ground和ρlater对模型的反映变化相似，但是ρlater-ground会略高，两者相对误差在8%～9%之间；τ/R<4.5时，晚期视电阻率相差更大，极值可达40%.在H、K、A、Q三层模型中，当τ/R>3.1更接近真实电阻率，并且当中间层出现时，视电阻率会出现变化，从变化中可见，电性源地-空瞬变电磁对低阻层反映更强；利用晚期视电阻率对早期数据计算时，会出现很大误差，对晚期数据进行计算时，虽然相对误差减小，但是这种误差仍然不可忽略.

2.3 全期视电阻率

2.3.1 基于垂直B-场的全期视电阻率

根据垂直Bz表达式，可以分为两部分：

Bz(t)=Bz0+ΔBz,

(14)

(15)

ΔBz=

(16)

令

(17)

(18)

(19)

计算地-空全期视电阻率时，我们根据上式分为两步进行计算：

(20)

(21)

ρ=ρ0+Δρ,

(22)

垂直磁场计算全期视电阻率时，由于该分量与电阻率呈单调关系，我们采用二分法，该方法也是求取非线性方程常用的方法.利用该方法求取全期视电阻率的流程如图9.

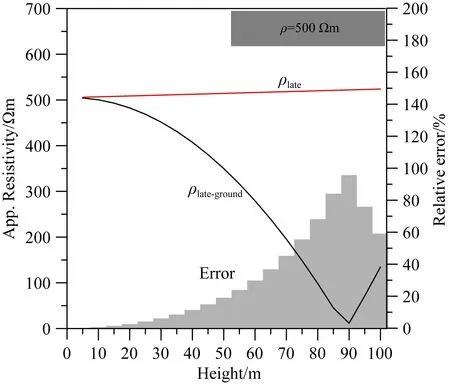
图8 晚期视电阻率随高度变化图Fig.8 Later apparent resistivity changes with height

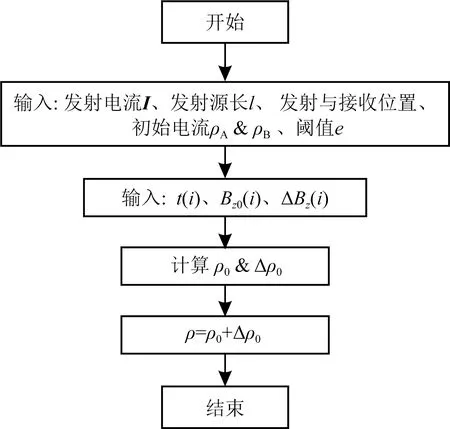
图9 B-场全期视电阻率计算流程图Fig.9 Flow chart of apparent resistivity calculation of B-field

2.3.2 基于垂直感应电压ε的全期视电阻率

感应电压计算全期视电阻率时，我们利用白登海等(2003)计算地面磁性源瞬变电磁全期视电阻率的策略，避免在对感应电压积分为垂直磁场过程中产生的较大误差，而选取迭代法对早、晚期视电阻率求解，并通过转折点构成全期视电阻率曲线.

(23)

(24)

可得

(25)

根据上述公式，我们称Q′0(t)和ΔQ′(t)为ε(t)的核函数，并通过核函数随u的变化规律.

由图10可知，在求取ρ0过程中，可以分为早期和晚期求取，在u>1.21求得早期视电阻率，在u<1.21求取晚期视电阻率，在拐点处，将该点的早、晚期视电阻率进行平均取值.同样的，计算Δρ时，在u<4.27求取晚期视电阻率，在u>4.27求取早期视电阻率，在拐点处做相同平均处理.

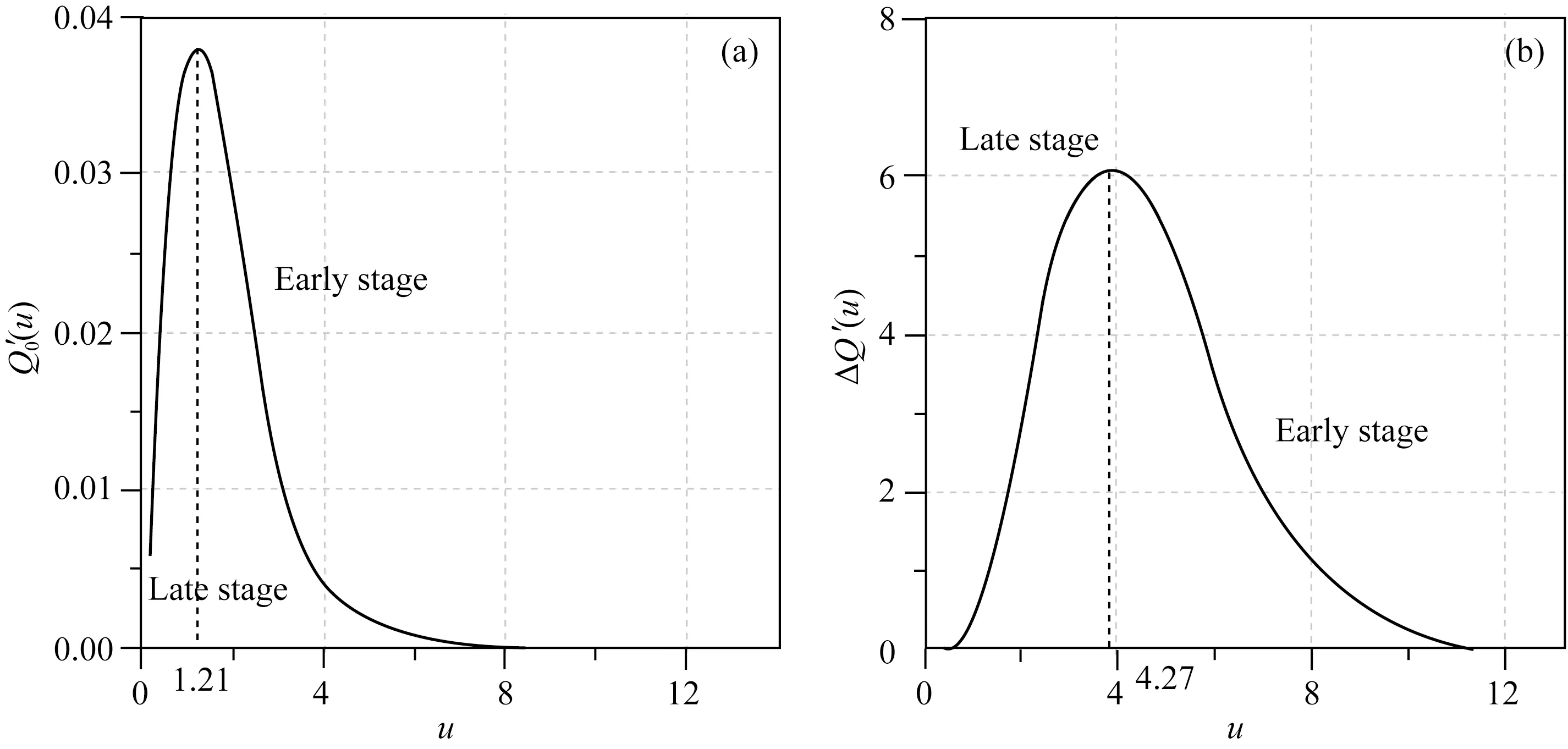
图10 核函数随u的变化特征(a) Q′0核函数与u的变化特征; (b) ΔQ′核函数与u的变化特征.Fig.10 The variation characteristics of kernel function with u(a) The variation characteristics of Q′0 with u; (b) The variation characteristics of ΔQ′ with u.

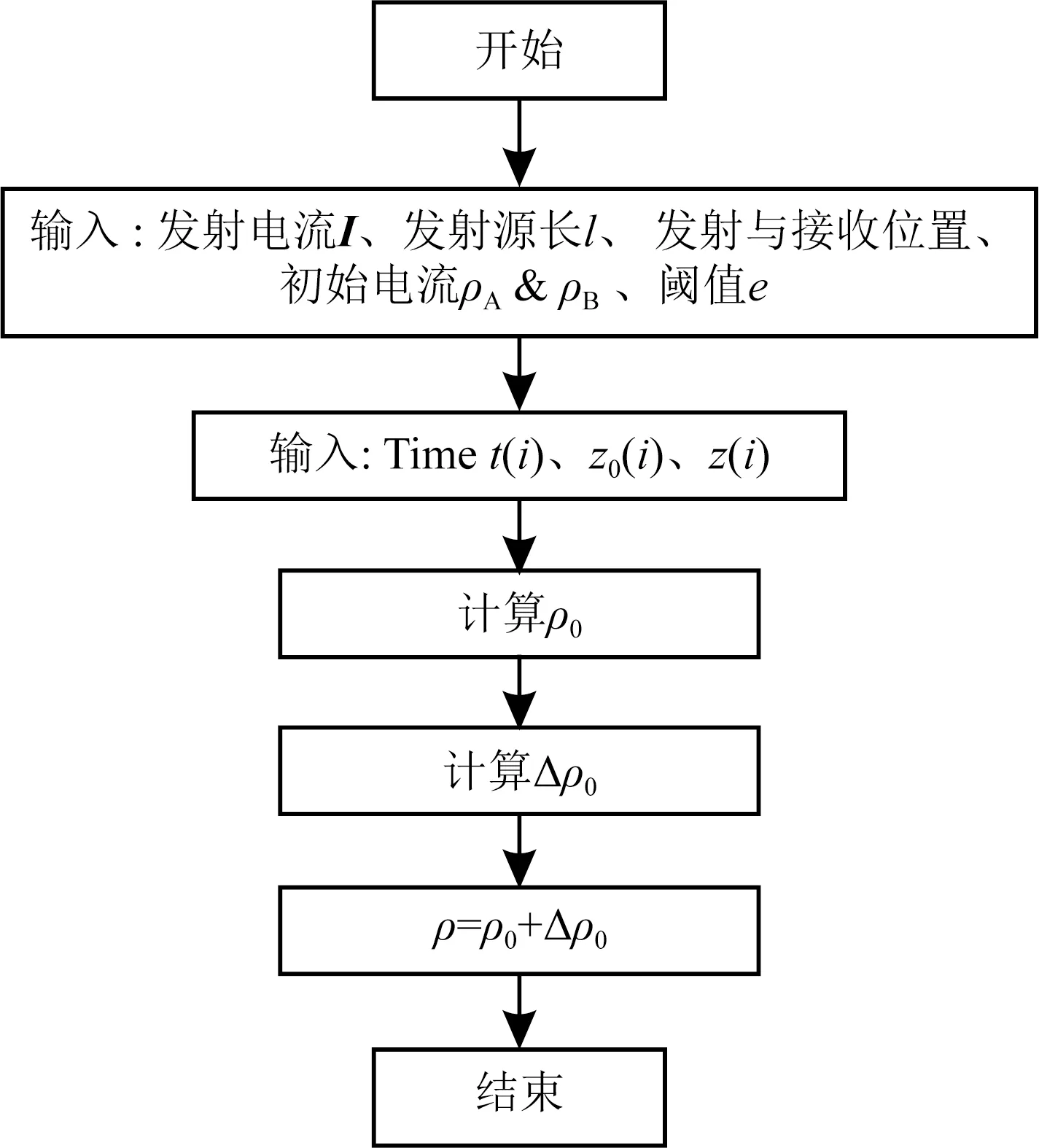
图11 基于感应电压全期视电阻率计算流程图Fig.11 Flow chart of apparent resistivity calculation of induced voltage

与利用B-场计算全期视电阻率相似，基于感应电压求取视电阻率分为两步，首先利用Bz0求取早期和晚期视电阻率，流程如图11.

我们利用三层模型，飞行高度为50 m，PE=10000 Am，r=500 m，赤道向接收，进行基于B-场及感应电压进行全期视电阻率计算.

由图12可知，利用B-场和感应电压计算全期视电阻率时都能够很好的反映地下介质的变化状况.但如果不考虑飞行高度，利用传统计算全期视电阻率时会在飞行高度的影响下降低视电阻率，而如果考虑飞行高度计算视电阻率时会消除高度带来的误差.如果在同一个测线中飞行高度不一致的情况下，利用传统忽略高度影响进行全期视电阻率计算时，极有可能出现“假异常”.

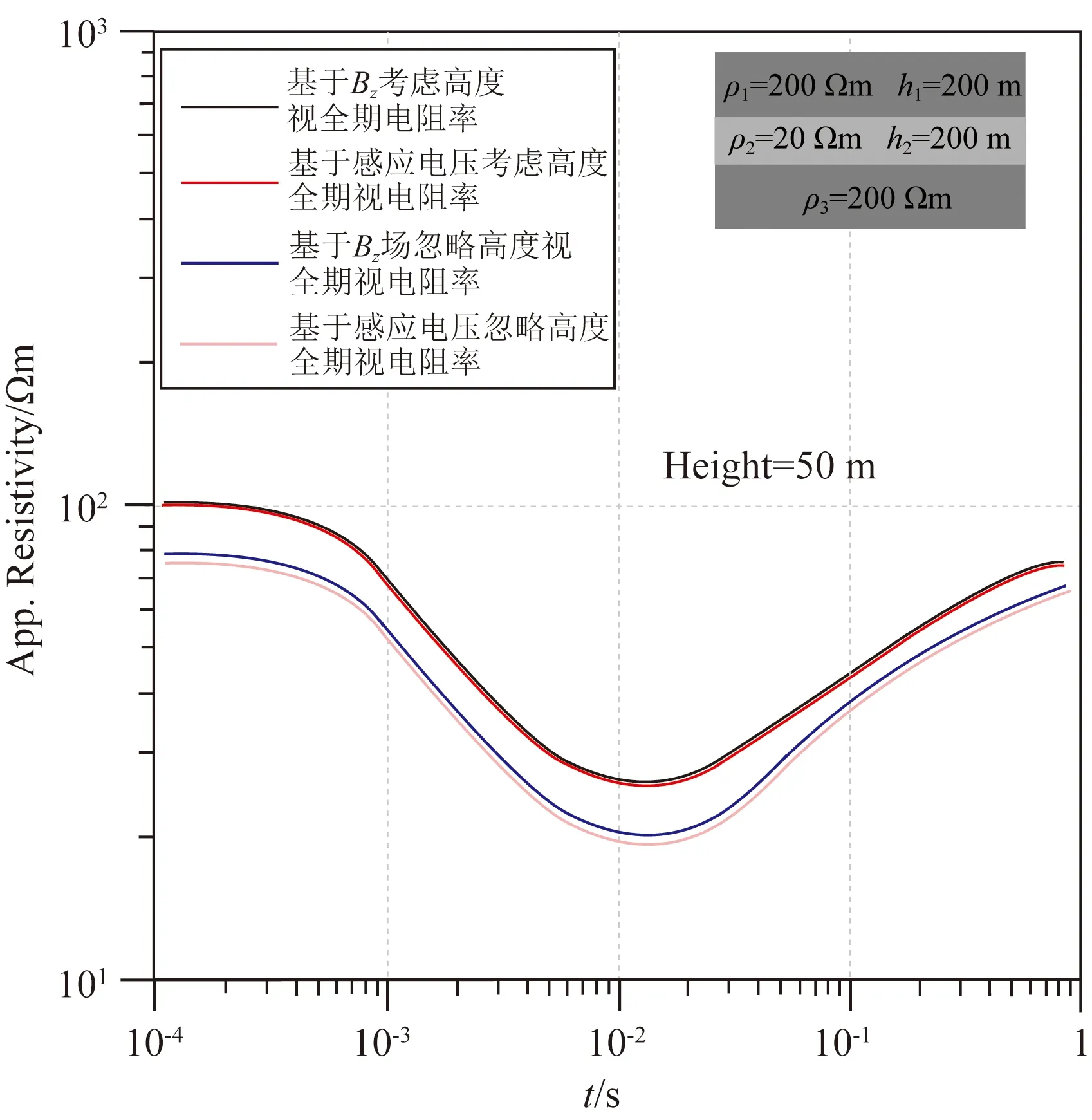
图12 基于B-场及感应电压计算全期视电阻率对比Fig.12 Comparison of apparent resistivity calculated based on B-field and induced voltage

3 成像深度

3.1 成像深度定义

在电性源地-空瞬变电磁法电阻率成像中，将时间参数转换成深度参数是构造电阻率-深度剖面的重要方面.在磁性源地面瞬变电磁法中的成像深度(闫述等, 2009)为

(26)

而在航空电磁法中，根据殷长春(2016)给出的成像深度为

(27)

但是在电性源地空瞬变电磁法中，由于出现了纵向电流，根据不同接收信号类别得到的成像深度也有所不同.为此，我们依据纵、横向感应电流扩散特点，将感应电流能量最大处定义为成像深度，以建立与扩散深度的关系.这是因为能量最大位置对信号响应的贡献最多.

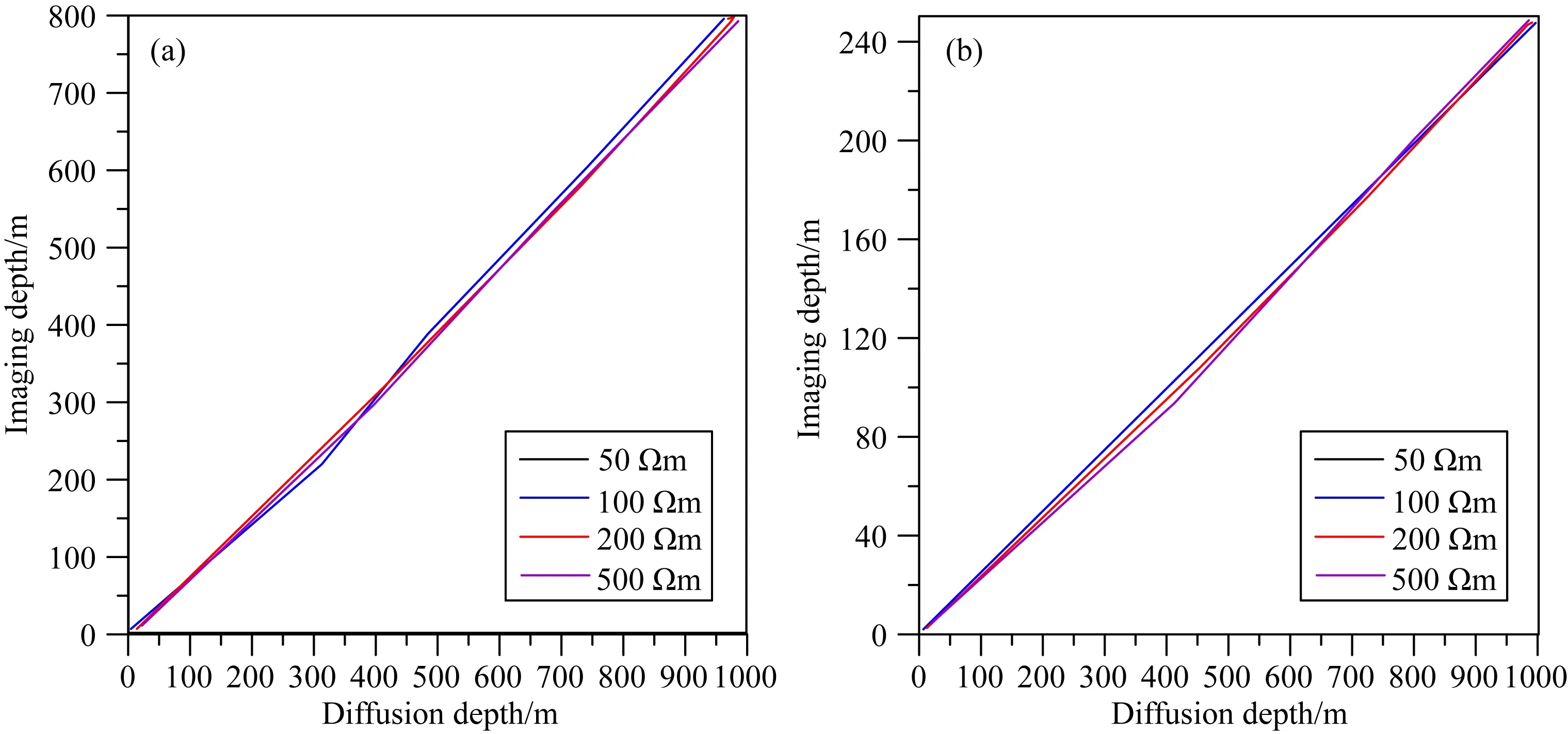
图13 成像深度与扩散深度关系图(a) 纵向电流下成像深度与扩散深度的关系; (b) 横向电流下成像深度与扩散深度的关系.Fig.13 Relation between imaging depth and diffusion depth(a) Relation between imaging depth and diffusion depth under longitudinal current; (b) Relation between imaging depth and diffusion depth under transverse current.

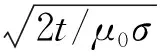
(28)

(29)

式中，δV和δH分别是考虑纵向电流和横向电流的电流能量最大处，即采用横向响应和纵向响应的成像深度.

3.2 探测深度的影响因素

在进行数据采集进行探测深度估算以设计最优化的采集方式时，往往要考虑影响探测深度的影响因素，如噪声水平、接收装置灵敏度和飞行高度等，相对于地面电磁法，地-空瞬变电磁法更易受噪声和灵敏度及飞行高度影响.

将公式(29)代入公式(3)，可得

(30)

由上式可知，影响探测深度有发射磁距(发射电流与源长的乘积)，接收装置有效面积，接收位置(偏移距、偏移角、飞行高度).

由图14a可知，飞行高度的变化对成像深度并不是单调的，在低空飞行时，随着高度升高成像深度减小，随之增大，这是因为高度的上升会更容易接收携带地质信息的短频波，探测深度更高，而高频波由于能量强，更易被消耗而不易被接收装置采集.由图14b可知，发射磁距的增强会增大探测深度，能量更强会使得感应电流深入地下，从而接收到更深的有效信号.由图14c可知，在短偏移距接收时，感应电流在偏移距更远时电流相对变弱，从而减弱探测深度.由图14d可知，在赤道向接收(φ=90°)逐渐减小到φ=52°左右时，探测深度几乎不变，偏移角度逐渐减小时，受电磁场分布影响，探测深度变化复杂，总体呈上升趋势.并且，电阻率的变化会影响探测深度，由于趋肤效应可知，低阻地区会降低探测深度，电阻率上升会增加成像深度.

图14 飞行高度和发射磁距对成像深度的影响(a) 飞行高度对成像深度的影响; (b) 发射磁距对成像深度的影响; (c) 偏移距对成像深度的影响; (d) 偏移角度对成像深度的影响.Fig.14 The influence of flight altitude and launch magnetic distance on imaging depth(a) The influence of flight altitude on imaging depth; (b) The influence of emission magnetic distance on imaging depth; (c) The influence of offset on imaging depth; (d) The influence of offset angle on imaging depth.

4 实例分析

大同市位于山西省东北部，煤炭资源丰富，众多的煤矿开采完成之后，会赋存大量的煤炭采空区.采空区的存在会大体出现两种情况，一种是采空区为空洞状态，另一个是富水状态.由于重力作用，会使得采空区往往成为低洼处，这就造成了采空区富水状态，而富水状况最少为几千立方.这些采空区的存在会极大影响人民生活和财产安全，也对煤矿的正常的生产生活造成了特别严重的隐患.

大同的煤炭主要为侏罗系和石炭二叠系煤系，又称为双纪煤田.大同煤田区域的石炭二叠纪的煤层主要为太原组和山西组，太原组含有2～10号煤，煤层厚度大约为0.1～52 m，3～5号煤是该组的主采煤层，平均厚度稳定在17.5 m左右；在山西组内，主要赋存4层煤层，是该组的主采煤层.

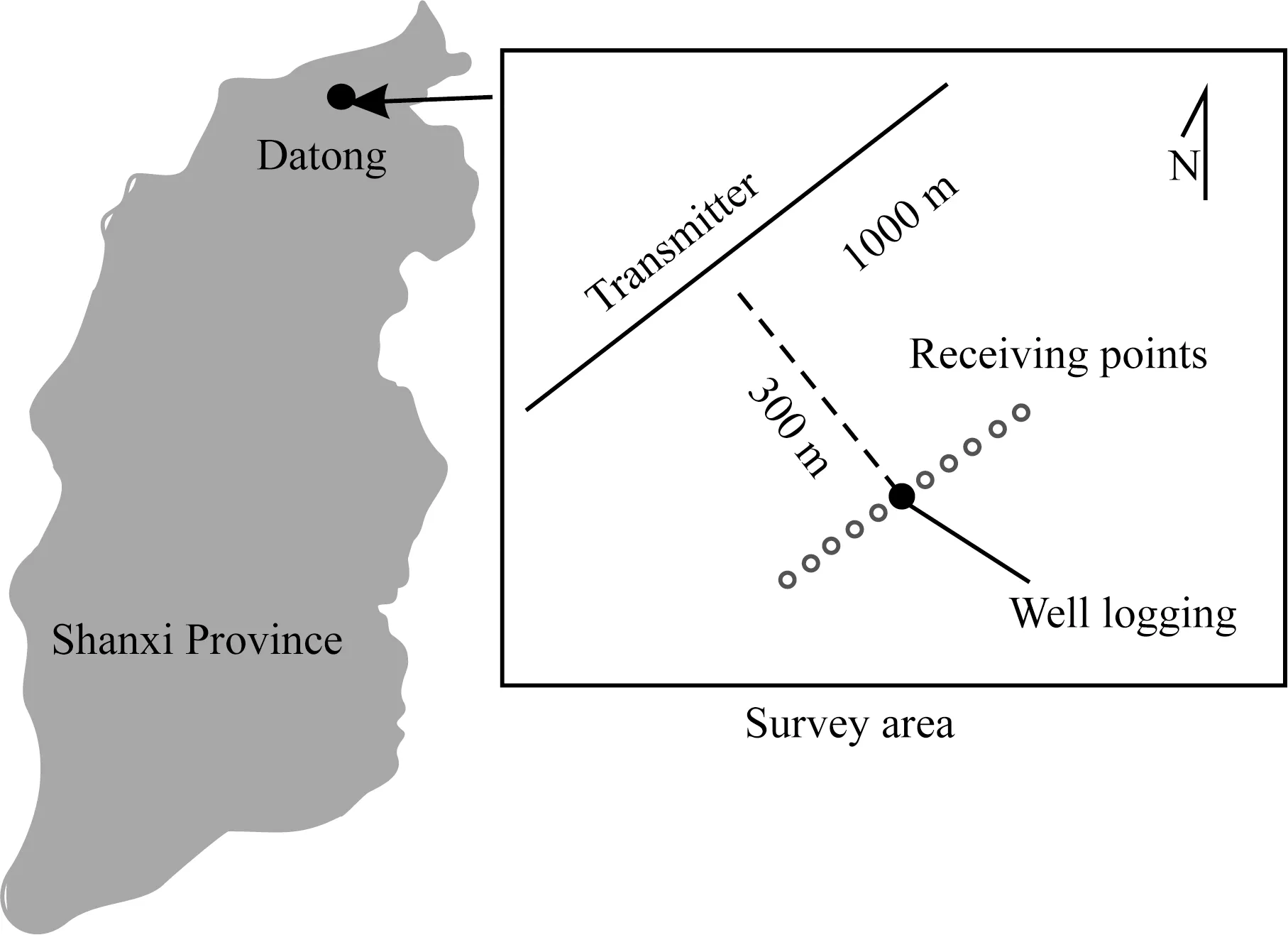
图15 测线布置图Fig.15 Survey line of SATEM

该试验区设置发射源长1000 m，偏移距300 m，测线长度600 m，点距5 m，测线设计如图15.发射电流10 A，波形为方波，基频25 Hz.接收线圈有效接收面积3000 m2，搭载在无人机平台上，在测点420～440 m间存在已知测井，勘探区域的选择参考Ma等(2020)提出的最佳观测区域.由图16a所示，传统电阻率-深度成像未考虑飞行高度及不同感应电流产生有效信号的差异，在实测过程中，高度影响会出现比实际地电结构电阻率整体偏小的结果，尤其是探测采空区等低阻靶体时，会扩大目标体的几何大小，降低了精确度.

图16b所示，当考虑飞行高度进行视电阻率计算时，与传统视电阻率相比，整体幅值增加，缩小了低阻目标体对周围的“同化”影响，而更加精确靶体位置并且强化了与深层基岩的区别；同时，考虑到垂直磁场由横向感应电流产生，成像深度会更加符合实际靶体的深度位置，两种成像方式对比，容易发现利用横向感应电流计算得到的成像深度会“升高”，结果中的视电阻率极小值点在深度250～270 m处，相比图16a结果，其极小值位置在300～400 m之间，根据图17中的由测井数据得到的岩性分布状况，水位深度267.96 m，厚度2.25 m，结果与图16b更加吻合.

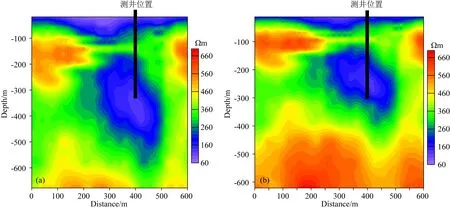
图16 视电阻率-深度成像对比(a) 传统视电阻率-深度成像； (b) 考虑高度及感应电流差异的电阻率-深度成像.Fig.16 Depth-apparent resistivity imaging contrast(a) Traditional apparent resistivity-depth imaging; (b) Resistivity-depth imaging considering the difference of height and induced current.

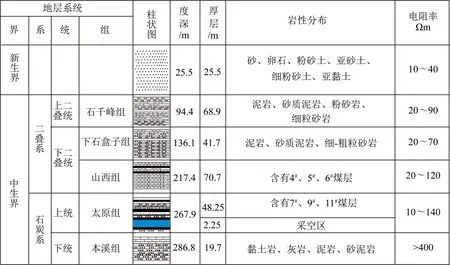
图17 基于测井数据的岩性分布图Fig.17 Formation stratigraphy of the mining area based on well logging from boreholes

两种视电阻率-成像结果对比表明，考虑感应电流差异更加符合瞬态电磁场的建场机制，考虑飞行高度使得结果更加精确.

5 结论

基于电性源半航空瞬变电磁法的电阻率-深度成像充分考虑到了包括纵向电流和横向电流的感应电流在向下、向外扩散时感应出横向和纵向响应，同时充分考虑了飞行高度对视电阻率计算的影响.在进行该方法研究、有效性验证及应用过程中，可以得到主要结论如下：

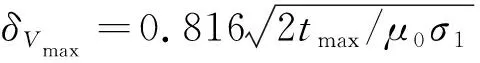
(3)基于地-空方法的视电阻率与将地-空数据简单进行地面视电阻率计算的结果相比，两者出现很大差异，飞行高度会影响传统视电阻率-深度成像的结果，增大与真实靶体位置的误差.

(4)考虑高度及感应电流差异的电阻率-深度成像突出了地-空方法的特点，提高了勘探精度，指导了该方法的实际应用.

致谢感谢中科院地质与地球物理研究所薛国强研究员课题组和山西煤田地质综合普查队在野外试验和本文的帮助和支持.

附录A

电性源地为了求解电偶源激发的瞬变电磁场，引入磁矢量位A：

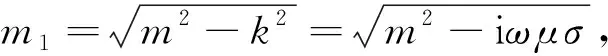
Ar=Axcosφ,

(A3)

Aφ=-Axsinφ,

(A4)

所以可得垂直磁场分量：

所以

垂直磁场分量就可以写成

(A11)

可以将上述公式分为两部分，可以写为

(A12)

当频率几乎为0时，可以认为是稳定场或者直流电源引起的电磁场，我们根据当kR≪1,kr≪1时：

(A13)

上述公式与通过毕奥-萨法尔公式计算的稳定场相同，并且我们可以写成

Hz=Hz0hz,

(A14)

所以，归一化为

(A15)

(A16)

(A17)

上式中，

(A18)

由于

(A19)

(A20)

可以得到在赤道向(φ=90°)垂直磁感应强度：

(A21)

可以得到在赤道向(φ=90°)垂直磁感应强度：

(A22)

感应电动势为