关于伪Drazin可逆的算子矩阵

王国栋，郭世乐，陈焕艮

(1. 杭州师范大学理学院,浙江 杭州 311121; 2. 福建技术师范学院电子与信息工程学院,福建 福清 350300)

0 引言

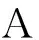
(1)ABC=0,CBC=0,BDC=0,D2C=0;

(2)CAB=0,BCB=0,DCB=0,A2B=0.

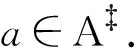
1 算子矩阵

首先给出一些需要用到的引理.

证明见文献[1, 定理 5.4].

□

证明见文献[1, 定理 5.3].

□

由于a2和ba具有伪Drazin逆,因此M和N具有伪Drazin逆.我们验证

于是,由引理1可知,P2具有伪Drazin逆.再次利用文献[2,引理2.8],P具有伪Drazin逆.证毕.

□

证明令M=P+Q,其中

我们验证

□

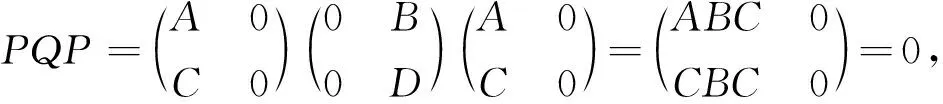
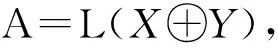
证明注意到

□

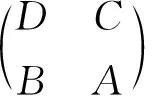
接下来,给出一个数值例子来说明定理1的结果.

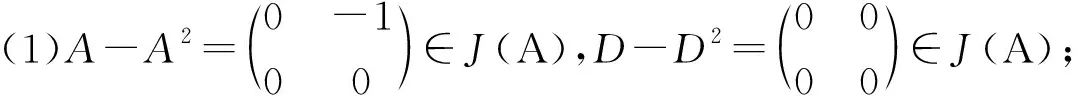
(2)BC=0,DC=0.

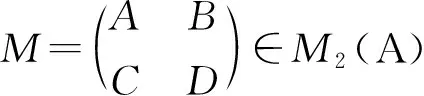
2 谱条件

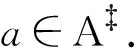
于是

□

□

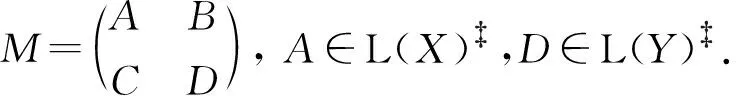
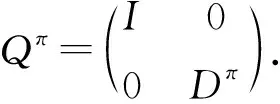
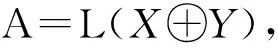
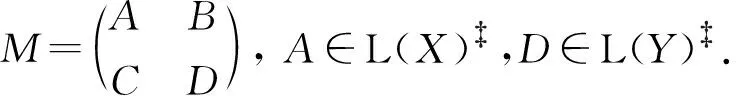
证明类似于推论1，由定理2即得.

□

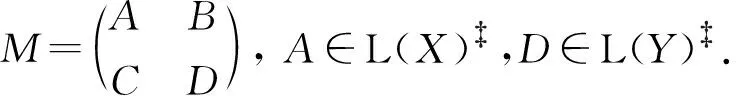
证明令

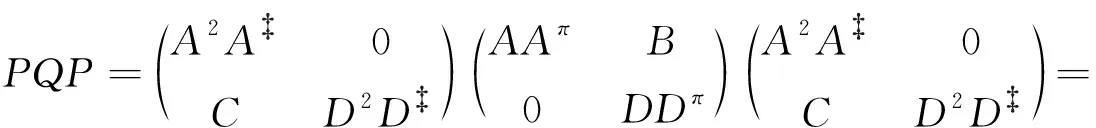
由引理3可知,定理3得证.

□

证明注意到

□

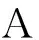
(2)D=D2;

咨询公司的做法确有不妥。从您的介绍来看，若您所述属实，那么根据《企业职工带薪年休假实施办法》中第三条“职工连续工作满12个月以上的，享受带薪年休假”的规定，您今年可以享受带薪年休假。但现在的问题是：您得证明自己已连续工作1年以上。

(3)BD=0;

(4)(I-D)C=0.

3 Schur矩阵

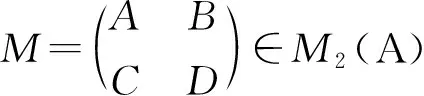
证明设M=P+Q,其中

显然,P1具有伪Drazin逆,只要证P2具有伪Drazin逆.注意到

可以验证

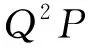
由引理3可知,M具有伪Drazin逆.

□

证明设M=P+Q,其中

我们可以验证

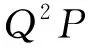
由引理3可知,M具有伪Drazin逆.

□