直线递减期累计产量新模型的建立与应用 ——以靖安油田五里湾开发区为例

康志勇，周明旺，曾宪红，李晓涛，闫鑫洋

（中国石油辽河油田分公司勘探开发研究院，辽宁盘锦 124010）

Arps 于1945 年提出的三种递减类型（指数递减、双曲线递减和调和递减），即传统Arps 递减理论已在国内外得到广泛应用[1–6]，其中指数递减应用最为普遍，如DeGolyer and MacNaughton 等国际咨询公司普遍采用指数递减预测产量。2004 年以来，从事开发研究的科研人员逐渐将传统Arps 递减理论扩展为广义Arps 递减理论，即将传统Arps 递减指数的应用范围由[0，1]扩展到（–∞，+∞），并导出广义Arps递减理论之直线递减期累计产量公式[7–12]（以下简称老模型）。为了解决老模型中由于存在明显系统误差，预测精度有限的问题，本文依据直线递减的特点，系统建立了累计产量和技术可采储量理论 方程（以下简称新模型）。新模型计算方法简便快捷、计算精度高于广义Arps 递减理论导出的直线递减期累计产量和技术可采储量公式，从而为客观评价累计产量及技术可采储量提供了有效的实现途径和广阔的应用前景。

1 直线递减模型的建立

1.1 直线递减的特点

直线递减是指产量递减呈线性变化，且有如下特点：一是任何统计单位的产量递减指数恒为- 1；二是直线递减期稳定日产量、稳定月产量或稳定年产量均为等差数列，即任意两个相邻稳定产量之间的差值为常数（稳定日产量数列的等差为q0Ddi、稳定月产量数列的等差为m2q0Ddi或Q0Dmi、稳定年产量数列的等差为(12m)2q0Ddi或Q0Dyi）。根据直线递减的特点可导出系列递减参数的相关数学表达式。

1.2 稳定产量

根据稳定产量直线递减数列的等差可导出产量递减生产到第t 天（或第x个月或第y 年）的稳定产量数学表达式：

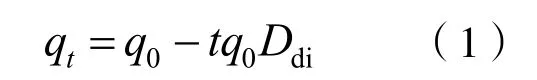
式中：tq 为递减生产第t 天的稳定日产量，m3或t；q0为初始稳定日产量，m3或t；t 为递减生产天数，d； Ddi为初始日递减率。

当式（1）中递减生产时间为月时，相应产量为月产量，递减率为初始月递减率；当递减生产时间为年时，相应产量为年产量，递减率为初始年递减率。其中，初始月产量和初始年产量与初始稳定日产量和初始日递减率等参数之间存在固定函数关系：

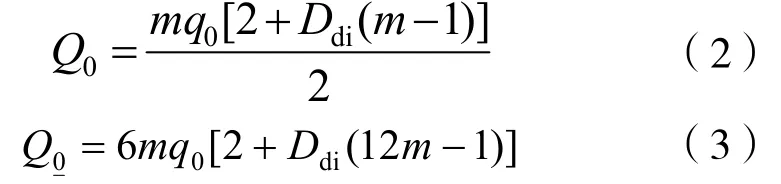
式中：Q0为初始月产量，m3或t；Q0为初始年产量，m3或t；m为平均每个月递减生产天数（31 1＜≤m），d。

对于无稳产期的评价单元，初始月产量和初始年产量为虚拟产量，计算累计产量时不能将初始月产量或初始年产量直接计入递减前的累计产量中。

1.3 初始递减率

根据初始递减率定义[7]和评价单元直线递减生产特点可采用任意相邻稳定日产量或相邻稳定月产量或相邻稳定年产量导出的初始日递减率的数学表达式：

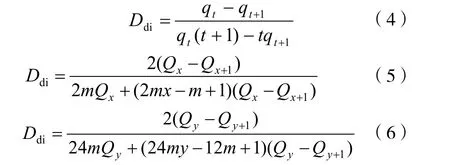
式中：1+tq 为递减生产第 1+t天的稳定日产量，m3或t；Qx、Qx+1分别为递减生产第x个月、递减生产第x+1个月的稳定月产量，m3或t；x为递减生产日历月数，mon；yQ 、1+yQ 分别为递减生产第y 年、递减生产第1+y年的稳定年产量，m3或t； y 为递减生产日历年数，a。

计算初始月递减率或初始年递减率所用公式形式与式（4）相同，只需将递减时间和产量单位进行相应变化。

1.4 递减期累计产量和技术可采储量

采用初始稳定日产量或初始月产量或初始年产量可导出直线递减期累计产量数学表达式：

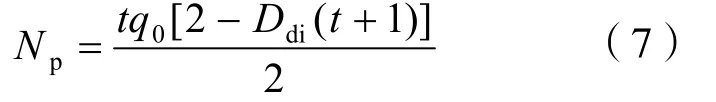
式中：Np递减生产第t 天（或递减生产第x 个月或递减生产第y 年）的累计产量（不含0q 及之前产量），m3或t。

当式（7）中的递减生产时间为月时，相应产量为初始月产量，递减率为初始月递减率；当递减生产时间为年时，相应产量为初始年产量，递减率为初始年递减率。

根据产量直线递减生产的特点可分别得到技术极限递减生产天数、技术极限递减生产日历月数和技术极限递减生产日历年数的数学表达式：

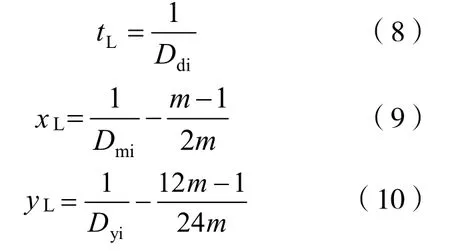
式中：tL为技术极限递减生产天数，d；xL为技术极限递减生产日历月数，mon；yL为技术极限递减生产日历年数，a；miD 为初始月递减率；yiD 为初始年递减率。

将技术极限递减生产时间方程与直线递减期累计产量方程结合可导出技术可采储量数学表达式：

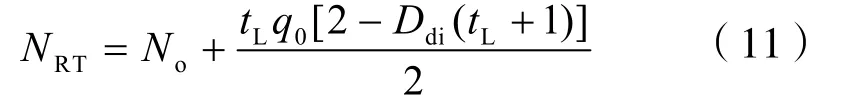
式中：RTN 为原油技术可采储量，m3或t；oN 为评价单元递减生产前原油累计产量，m3或t。

当式（11）中的技术极限递减生产时间为月时，相应产量为初始月产量，递减率为初始月递减率；当技术极限递减生产时间为年时，相应产量为初始年产量，递减率为初始年递减率。

1.5 直线递减模型适用性分析

严格地讲，递减指数等于1- 的评价单元均可采用直线递减模型评价递减期稳定产量和累计产量，但实际评价单元在递减生产过程中不完全遵循单一递减规律，特别是递减初始阶段呈直线递减的评价单元，到递减中后期并不一定依然遵循直线递减特点。因此，用直线递减模型预测评价单元产量时，产量变化要遵从持续、稳定、规律性变化的原则。

对于相邻稳定产量的差值大于平均差值%10±的评价单元，原则上不采用直线递减模型预测产量；对于递减生产到中后期的评价单元，用直线递减模型预测产量相对客观准确；对于只有较少初始产量递减生产数据的评价单元，尽管递减指数等于或近似等于 1- ，用直线递减模型预测评价单元中后期产量数据仍存在风险。

2 新老模型对比

当递减指数为1- 时，广义Arps 递减理论之直线递减期原油累计产量公式为[7–11]：

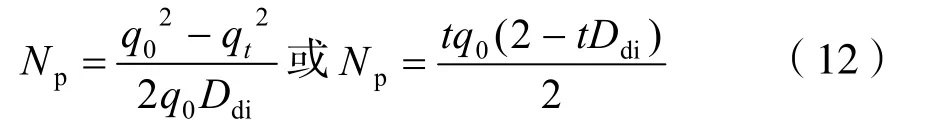
采用月产量或年产量计算递减期累计产量公式形式与式（12）相同，只需将递减时间、稳定产量、初始递减率等进行相应变化。

若评价单元直线递减期平均每个月递减生产25 d，则稳定日产量、稳定月产量、稳定年产量及递减期原油累计产量列于表1。分别采用老模型和新模型计算递减生产第900 天、递减生产第36 个月和递减生产第3 年的原油累计产量及误差情况。

根据表1 给出的理想直线递减生产数据可得到日、月、年的初始产量及初始递减率：初始日产量为50.00 m3、初始日递减率为0.001；初始月产量为1 265.00 m3、初始月递减率为25/1 012；初始年产量为17 242.50 m3、初始年递减率为600/2 299。

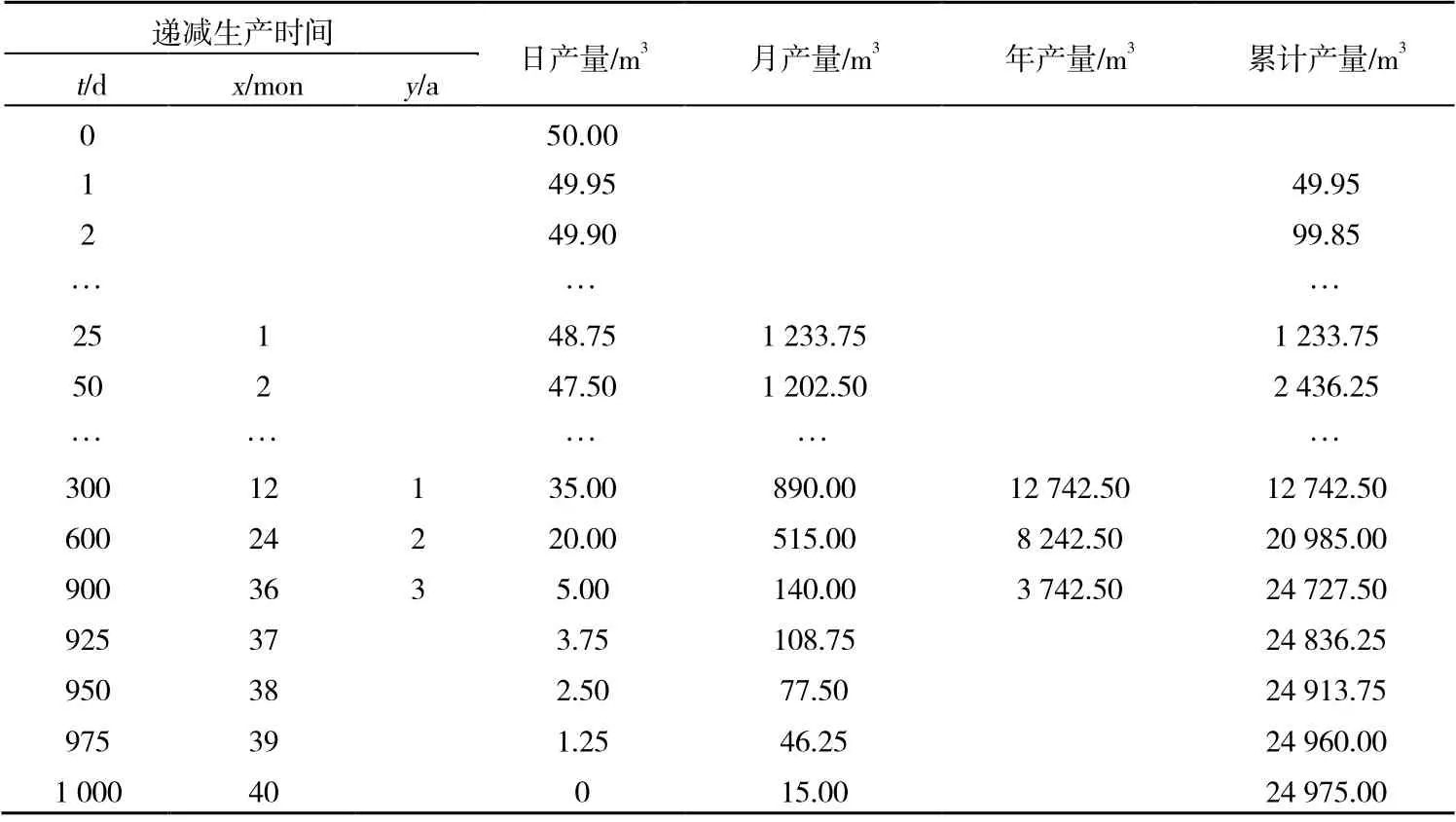
表1 直线递减生产数据表

采用新模型和老模型所计算的评价单元累计产量及误差对比情况如表2 所示。

表2 新老模型预测累计产量及误差对比

新模型计算递减期累计产量与实际产量完全吻合；老模型计算递减期累计产量均有误差，且以稳定年产量预测累计产量误差最大可达27.30%，用稳定日产量预测累计产量误差最小为0.09%。

3 应用实例

靖安油田五里湾开发区产层为三叠系延长组6段，1996 年投入试采，2000 年转入开发。该开发区投产第9 年进入直线递减期，历年年产量及累计产量情况详见图1 和表3。

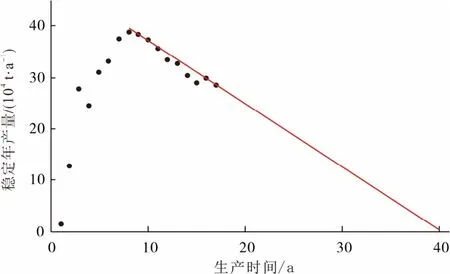
图1 五里湾开发区生产曲线

该开发区递减前累计产量206.57×104t，根据直线递减期相邻稳定年产量差值相等的特性，计算直线递减期相邻稳定年产量间的平均差值为1.22×104t，则据式（13）计算可得初始年产量为39.49×104t。

式中：Q1为递减生产第1 年的稳定年产量，据实际资料取值为38.27×104t；yQΔ 为直线递减期相邻稳定年产量间的平均差值，t。

由前述可知：

将式（13）与式（14）联立可解得初始年递减率为489/15797（或0.03）。

将初始年递减率和初始年产量分别代入式（1）和式（7）得稳定年产量和累计产量预测值（表3），预测值与实际生产数据相吻合。

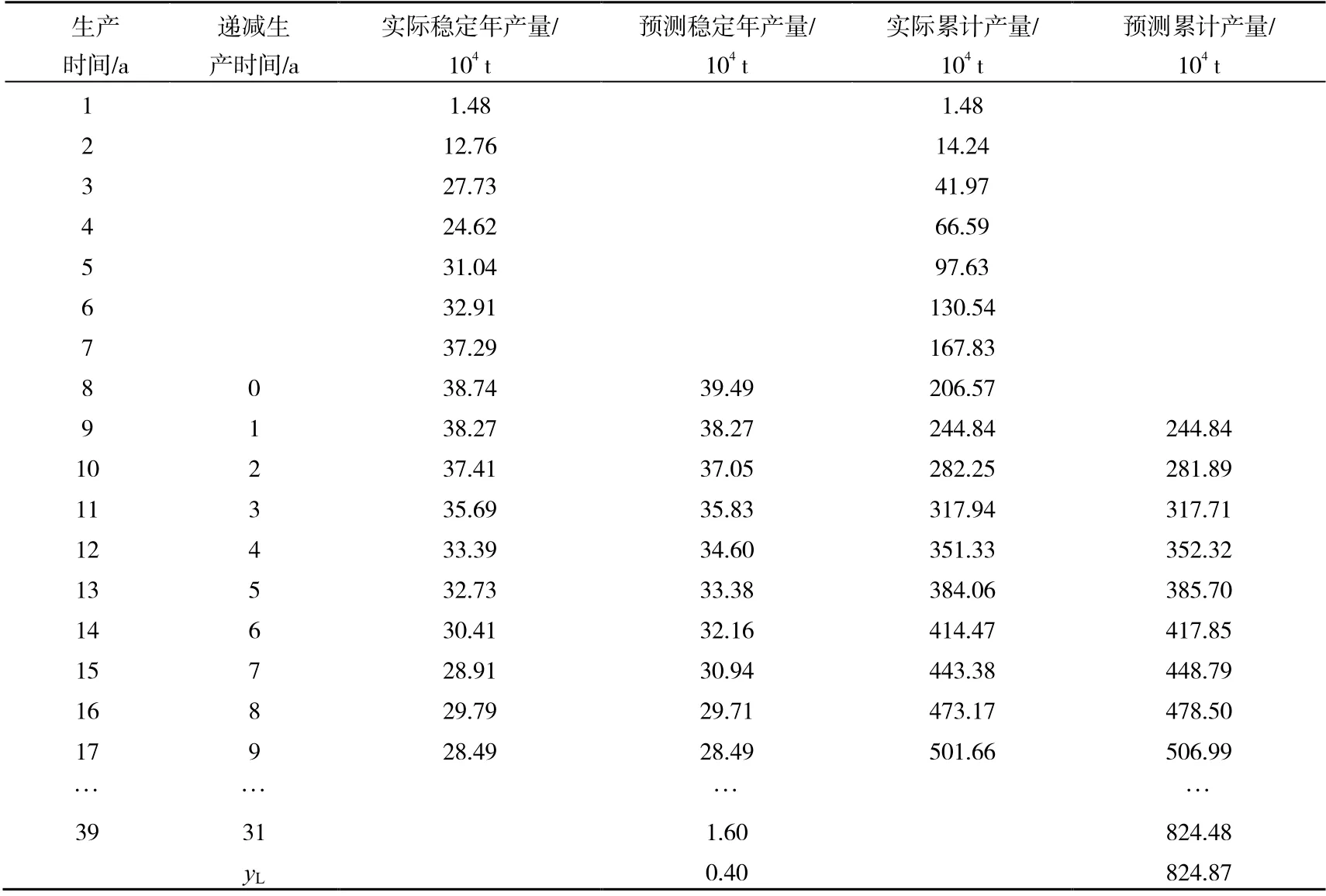
表3 五里湾开发区实际递减生产数据及预测数据对比

五里湾开发区平均每个月递减生产天数10～30 d，其递减期技术极限递减生产年数和开发区技术可采储量分别为31.806 a 和824.87×104t。

采用老模型计算五里湾开发区累计产量最大误差为3.36%，用新模型计算累计产量最大误差为1.22%（表4）。

已知该开发区探明地质储量6 067.00×104t，由此计算技术可采储量采收率为13.6%。

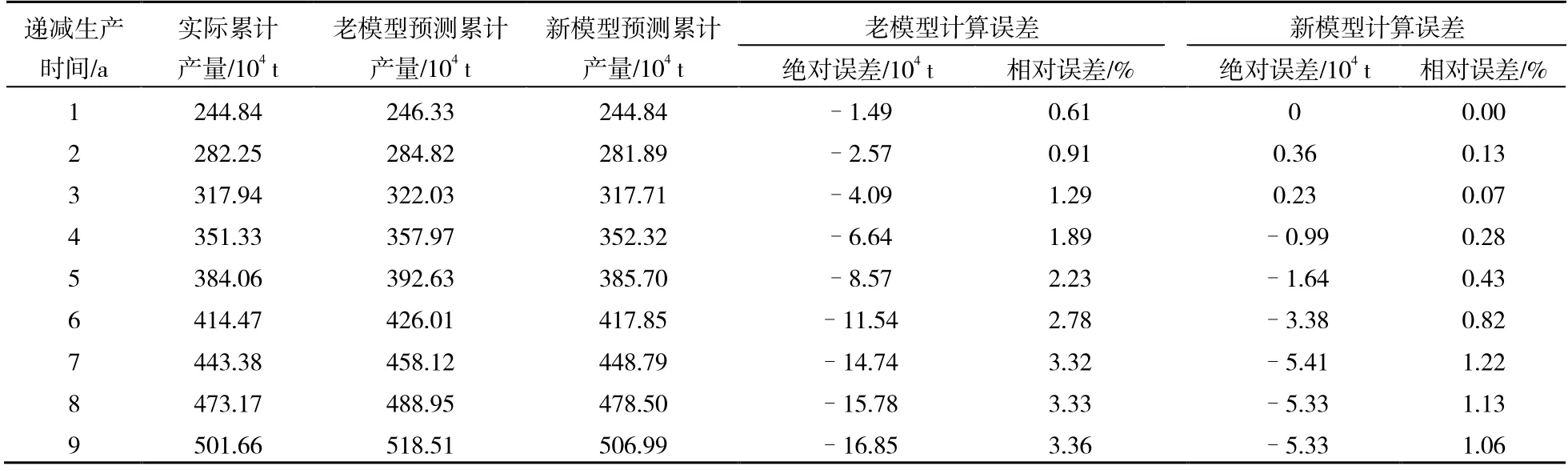
表4 五里湾开发区新模型与老模型预测产量误差对比分析

4 结论

（1）新模型和老模型分别导出的递减期累计产量及技术可采储量公式不同，计算精度差异明显：对理想直线递减数据而言，新模型计算相对误差远小于老模型计算的相对误差；对实际直线递减生产数据，新模型计算累计产量最大误差为1.22%，老模型计算累计产量最大误差为3.36%；新模型不仅是对广义Arps 递减理论的补充与完善，在实践中还具有广泛的实用性，且理论基础扎实可靠。

（2）新模型应用初始稳定日产量和初始日递减率等较易获取的参数可直接计算初始月产量和初始年产量，与回归法相比，极大地提升了初始产量的计算精度。

（3）新模型采用极限递减生产时间和初始产量及初始递减率计算可采储量，不仅计算方法简便实用，计算精度也得到了显著提高。