基于RSM与NSGA-Ⅱ的燃气灶外壳零件成形质量多目标优化

赵小云， 龚红英， 施为钟， 周志伟， 申晨彤， 嵇友迪

(上海工程技术大学 材料工程学院， 上海 201620)

家用燃气灶外壳是燃气灶的零部件之一，既有固定和保护燃气灶的作用，也增加了燃气灶具的美观和稳定以及易于清洁等附加性能。作为最直观的一个配件，其质量好坏也是灶具品质的一种重要的指标，同时也关系到家庭生活的安全问题[1]。选择合理的工艺方案对确保产品的成形质量和加工成本具有重要意义。利用CAE技术，可以预测板料拉深成形的流动情况、应力应变分布以及厚度变化，可以在模具制造前验证其成形的可能性，并且实现板材形状，尺寸和其他工艺参数的优化，同时也是提高效率和节省成本的有效方法。近年来，进行了许多关于数值模拟在板料成形工艺参数优化等方面的研究。Qiu等[2]运用eta/DYNAFORM完成了对发动机罩面板成形过程的模拟，研究了毛坯的初始形状和尺寸对其冲压成形性的影响。文艺等[3]采用二次响应面和蒙特卡罗方法对后排座靠背零件成形工艺参数进行了优化分析，对板料成形质量进行了优化。利用响应面寻优，灰色理论分析和正交试验抽样相结合的方式，熊文韬等[4]对某轻型卡车底板的成形参数进行优化，成功改善了轻型卡车地板的拉深成形质量。靳阳[5]运用DYNAFORM软件对内凹形零件的冲压成形过程进行了仿真模拟，基于正交试验分析法，研究了外转角、侧壁长度、内转角、拉伸高度、冲压速度、压边力和摩擦因数对零件壁厚的影响程度，得到了最佳的成形工艺参数组合。刘强等[6]以空调压缩机壳冲压成形的最大减薄率和最大增厚率为优化目标，利用DYNAFORM软件进行冲压成形数值仿真，采用径向基函数(RBF)神经网络结合带精英策略的非支配排序遗传算法(NSGA-Ⅱ)获得Pareto最优解集，并通过有限元分析验证方法的有效性。

由于工艺参数设置不合理导致的燃气灶外壳零件存在局部过度减薄等问题，课题组对燃气灶外壳零件拉深成形过程进行有限元仿真，采用BBD试验建立了工艺参数与最大减薄率、最大增厚率之间的响应面目标优化函数；利用NSGA-Ⅱ对2个目标函数进行求解，得到优化的Pareto最优解集并将最优解进行试验验证。

1 有限元模型

课题组以某燃气灶外壳为研究对象，三维模型如图1所示。燃气灶整体尺寸为680 mm×384 mm×50 mm，材料为304不锈钢，钢板厚度为0.7 mm，材料力学性能参数如表1所示。它属于嵌入式燃气灶外壳零件，整体形状为矩形，结构复杂且相对于Y轴对称。其顶部区域有2个凹台和1个凸台，且分布偏向一侧，因此该零件相对于X轴为非对称件，非对称的两侧的变形量存在差异。由于圆角半径r和宽度b之比r/b数值偏小，则将导致质变部分对圆角部位的变形显著，使圆角部位极易产生破裂缺陷，同时在零件的凸缘面受切向压缩易产生起皱缺陷。因此在进行拉深成形模拟分析中应当注意可能产生的缺陷问题[7]。文中试验都在确保本零件成形结果不产生开裂和起皱的前提下进行的。

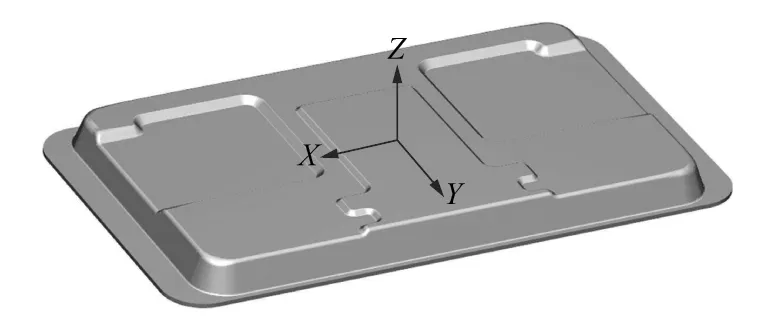
图1 燃气灶外壳三维模型Figure 1 3D model of gas stove shell

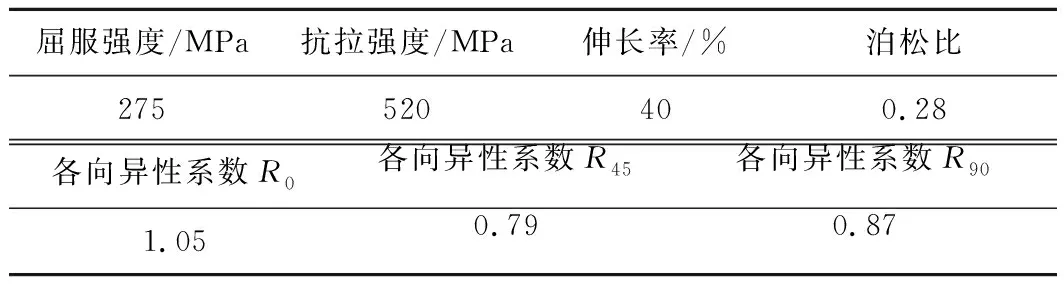
表1 SS304钢力学性能参数

以燃气灶外壳的三维模型为基准，在UG软件中设计该零件的凸、凹模和板料，输出IGS格式导入到DYNAFORM系统中。然后在DYNAFORM软件进行定义和网格划分，凹模，凸模、压边圈均定义为刚性体。其中压边圈是通过网格偏置生成，燃气灶外壳零件相关的有限元模型如图2所示。试验中，摩擦因数默认0.125，冲压速度设定2 000 mm/s，在压边圈上设置一圈等效拉延筋。本试验选用Barlat′89各向异性屈服准则建立材料模型，为基于平面应力条件下考虑面内各向异性提出的屈服准则，可以较好地描述各向异性材料的屈服行为，即适用于薄板金属成形分析，其表达式为：

(1)

其中：

(2)

(3)

(4)

(5)

式中：f为屈服准则函数；r0，r90为各向异性系数；σs为等效应力；σx，σy和τxy分别为主次应力和剪应力；m为非二次屈服函数指数,对钢而言m=6;x,y和z分别为平行于轧制方向、垂直于轧制方向和垂直于板平面方向;a,h和p为表征各向异性的材料参数。

对零件成形工艺参数进行设置，均采用Closure控制上下模闭合，gap设置为1.05～1.20倍数的料厚。运动过程为凹模向下运动压住板料，然后压住压边圈一起向下运动，直到凸模位置，完成零件冲压成形过程。

图2 有限元模型Figure 2 Finite element model

2 响应面试验设计及分析

虽然可以获得较好的拉深成形效果，但是厚度变化中最大减薄率较大，因此采用中心复合试验[8]设计建立工艺参数与目标间的二阶响应面模型，结合NSGA-Ⅱ算法实现多目标优化[9]，使得模拟结果满足最大减薄率和最大增厚率的条件下获得较好的拉深成形效果。

2.1 试验设计

试验选取圆角半径A、压边力B和模具间隙C3个工艺参数作为优化自变量，将最大减薄率y1和最大增厚率y2作为模型响应值。由于燃气灶外壳零件成形工艺参数和优化目标之间具有高度非线性变化特点，根据BBD设计原理采用多项式对目标函数进行拟合，其二阶多项式[10]模型可表示为

(5)

式中：β0,βi,βii,βij均为多项式待定系数；k为设计变量的数量；xi为设计变量集合；ε为次要误差。

试验各工艺参数的因子和水平表如表2所示，采用DYNAFORM进行模拟试验前处理设置，在Ls-Dyna求解器中进行数值运算，获得的17组试验模拟仿真结果如表3所示。

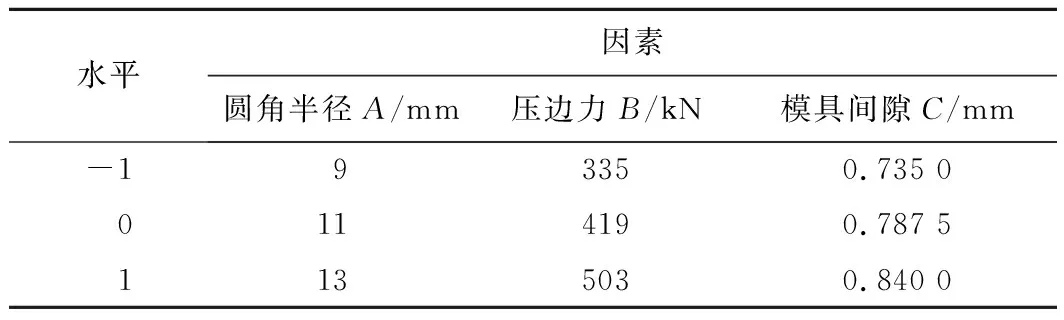
表2 工艺参数因子与水平

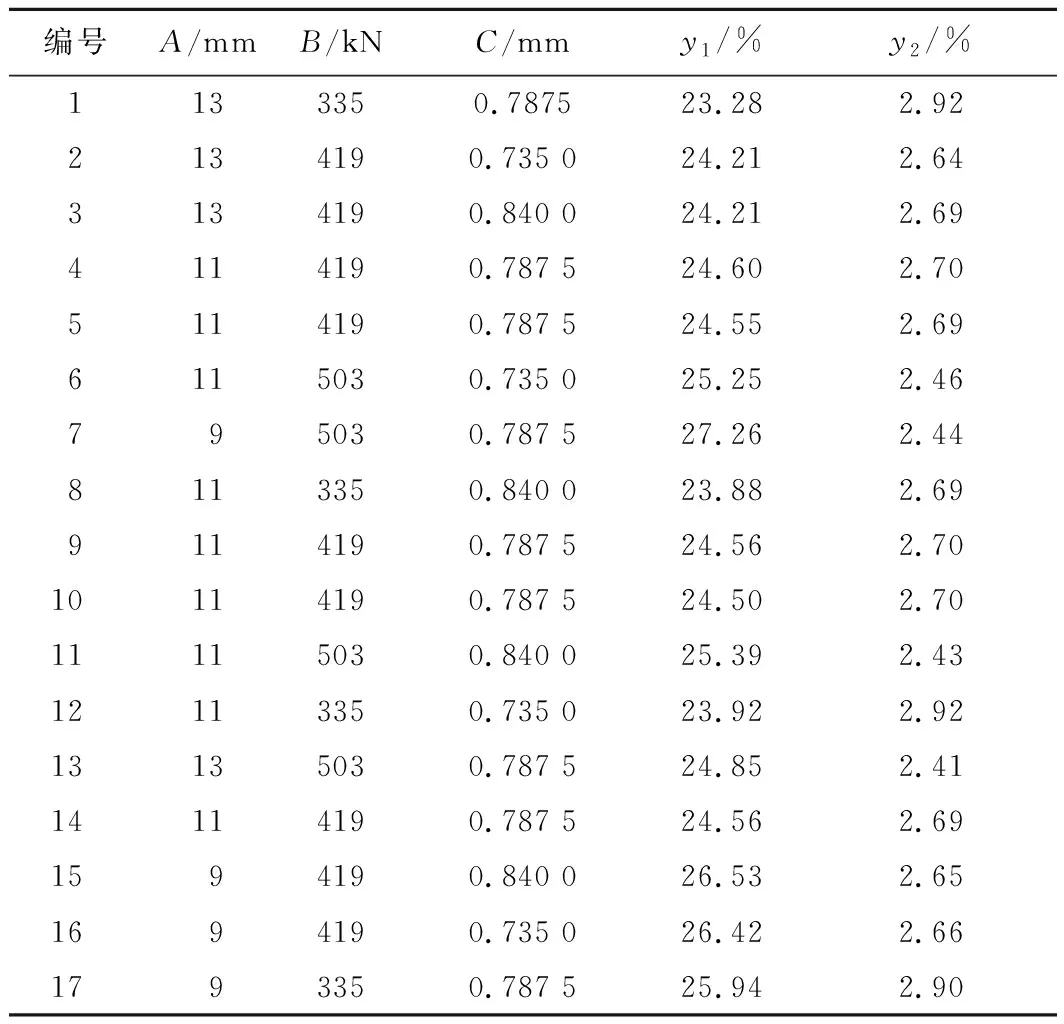
表3 试验方案与结果

2.2 方差分析

对表3试验结果进行数学分析，考虑各工艺参数间的交互作用，线性和平方项采用最小二乘法进行拟合，建立目标y1,y2与设计变量的非线性回归模型，响应目标函数为：

y1=55.242 02-4.928 24A-3.601 19×10-3B-3.775 51C+3.720 24×10-4AB+0.0102 04BC+0.189 65A2;

(6)

y2=-24.925 92+4.374 27A-0.028 99B+58.082 77C+4.017 86×10-3AB-7.714 29AC+0.011 338BC-0.202 50A2-4.499 72×10-6B2-14.240 36C2-1.860 12×10-4A2B+0.357 14A2C。

(7)

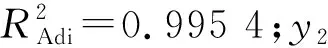
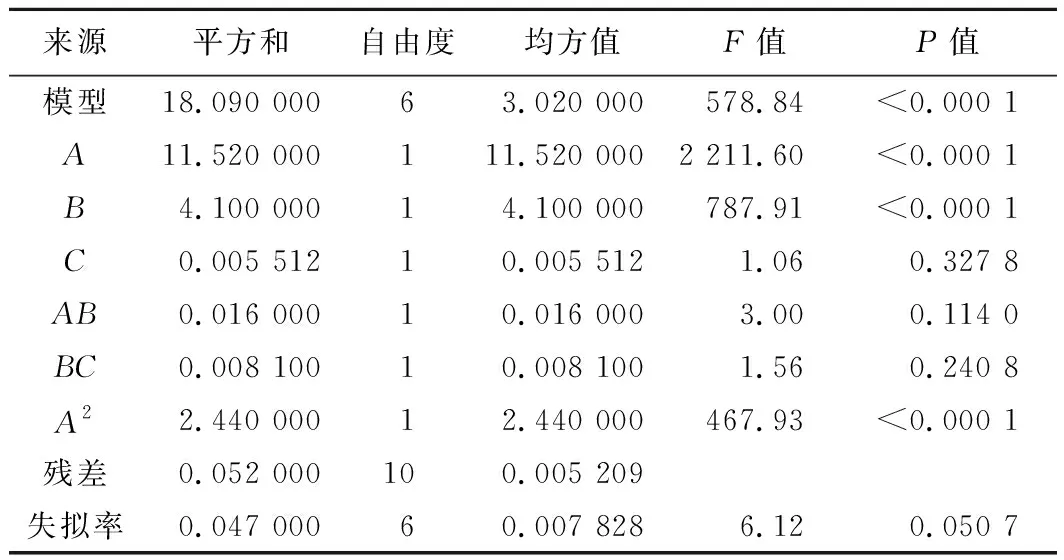
表4 最大减薄率y1方差分析

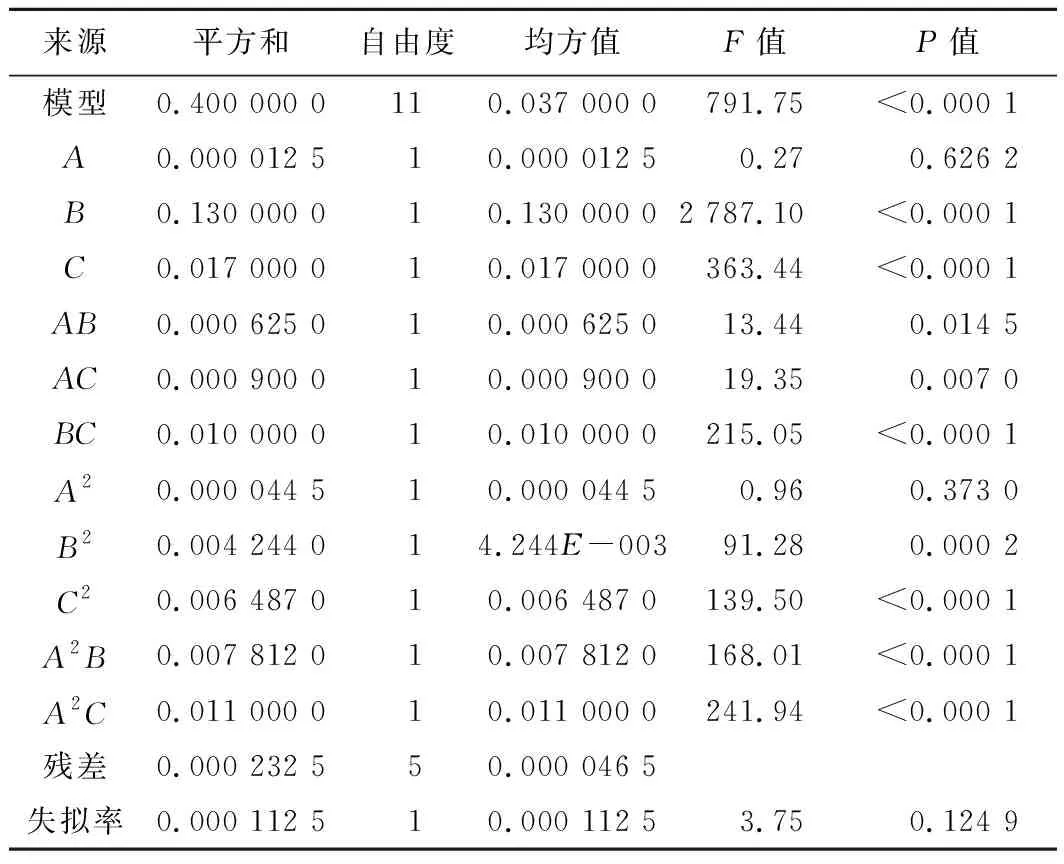
表5 最大增厚率y2方差分析

对影响最显著的交互因素进行分析，影响y1的交互因素最显著的为A和B，影响y2的交互因素最显著的为B和C，三维响应面与等高线图如图3～4所示。由图3可看出，当C=0.787 5 mm时，圆角半径减小及压边力增大的情况下，减薄率显著增大，这是因为随着压边力增大，板料与压边圈以及凹模之间的摩擦阻力随之增大，材料的流动会受到更大的阻力，使得材料开裂倾向增大。圆角半径对零件成形质量的影响很关键，圆角半径减小增加了材料进入凹模的阻力，便增加了一些危险位置的开裂趋势；圆角半径过大，会使得零件成形不完整。由图4可知，当A=11 mm时，模具间隙和压边力增大时，最大增厚率减小，且压边力的影响作用更大。工艺参数对减薄率和增厚率的影响规律不同，为保证零件具有较好的成形质量同时使得y1和y2尽可能小，需要对多目标进一步优化以得到最佳工艺参数。

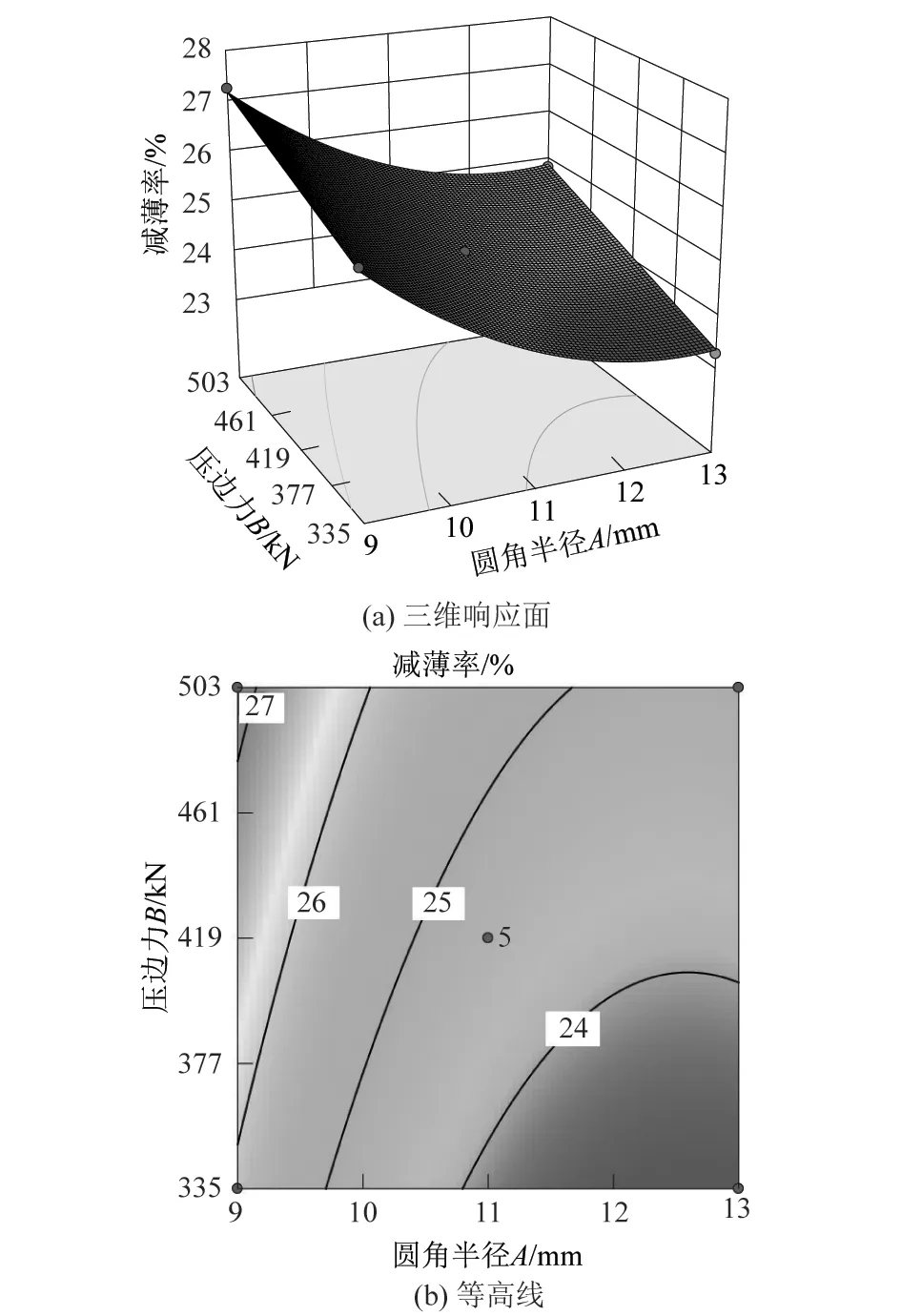
图3 C=0.787 5 mm时，A和B交互作用下y1的三维响应面和等高线图Figure 3 Three-dimensional response surface diagram and contour diagram of y1 under interaction of A and B at C=0.787 5 mm

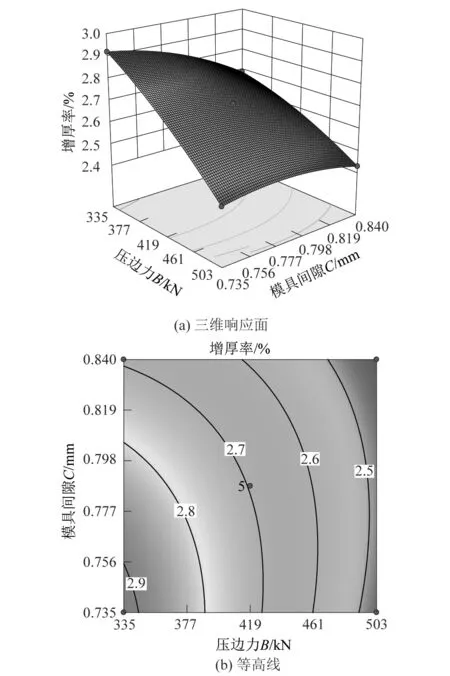
图4 A=11 mm时，B和C交互作下y2的三维响应面和等高线图Figure 4 Three-dimensional response surface diagram and contour diagram of y2 under interaction of B and C at A=11 mm

3 优化设计及试验验证

3.1 多目标遗传算法Pareto最优解集

遗传算法(genetic algo rithm，GA)是由美国的Holland教授提出的，是通过模拟生物界的进化过程并在种群中寻找最优解的优化方法。然而最优解通常是一个解集，且解与解之间有时是无法进行权衡的，可能对于一个目标函数而言为最优解，却对另一目标函数并非最优。对于多目标优化问题，根据以上定义在遗传算法基础上引入Pareto概念，提供可行解区域中的一些折中解[11-12]。

为使得成形后的零件最大减薄率和最大增厚率符合零件厚度减薄要求，同时也符合成形质量要求，根据响应面y1,y2目标函数,建立多目标优化模型和模型约束条件：

Fmin[y1(%),y2(%)]

(8)

约束条件：

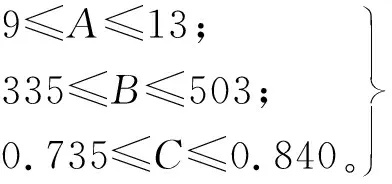
(9)

3.2 带精英策略的改进型多目标遗传算法(NSGA-Ⅱ)优化

NSGA-Ⅱ是NSGA的改进型遗传算法，提出快速非支配排序算法，采用拥挤度和拥挤度比较算子，使解集中的个体均匀扩散到整个Pareto域，同时引入精英策略扩大采样空间，提高种族水平，广泛应用于多目标优化。采用MATLAB软件设计，对目标函数及约束条件进行NSGA-Ⅱ优化设计，其中遗传算法相关参数设置为：种群规模200，迭代次数50，交叉概率0.9，变异概率1/3。运行得到如图5所示的NSGA-Ⅱ的Pareto优化前沿。

根据图5所示，NSGA-Ⅱ预测的结果显示，整体趋势上减薄率会随着增厚率的减小而增大。在Ⅰ区中，增厚率和减薄率的关系呈近似反比例函数关系，前期增厚率减少量大，而减薄率增量小，当减薄率为23.4%后，增厚率减少放缓；在Ⅱ区中，减薄率增大和增厚率降低的趋势呈线性关系。预测的增厚率数值较小，同时变化量较小，引起起皱的可能性较小，而开裂是燃气灶外壳零件的主要成形缺陷，因此，在Pareto最优解集中，选取减薄率最小的优化结果如表6所示。

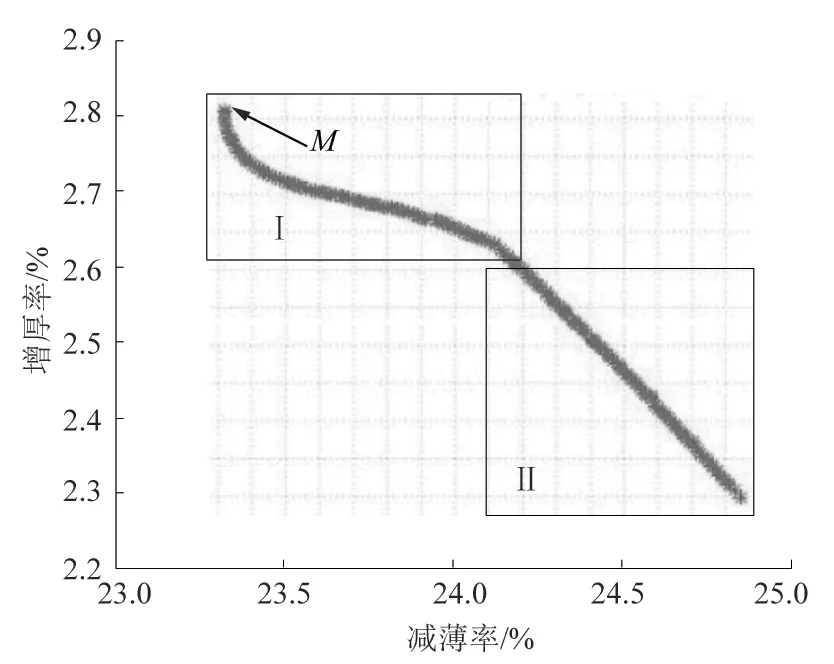
图5 NSGA-Ⅱ多目标优化Pareto前沿Figure 5 Pareto frontier of NSGA-Ⅱ multi-objective optimization

表6 NSGA-Ⅱ部分解的取值

3.3 验证

由表6可知，NSGA-Ⅱ预测的最大减薄率为23.32%，最大增厚率为2.8%，减薄率满足工程上低于30%的要求。因此将工艺参数取整：圆角半径为13 mm；压边力为335 kN；模具间隙为0.84 mm。

将优化后的工艺参数导入DYNAFORM软件进行验证，成形极限图(foming limit diagram, FLD)和减薄率云图如图6(a)和图6(b)所示。由图6(a)可知，拉深件内部为安全区域，边缘上有起皱，成形后的燃气灶外壳零件无开裂缺陷；由图6(b)可知，减薄率最小区域为底部圆角部分，在凸缘部分为增厚区域，数值模拟的y1为23.39%，与NSGA-Ⅱ预测值相差0.09%，y2为2.96%，与预测值差0.16%,说明NSGA-Ⅱ具有良好的全局优化和预测能力。

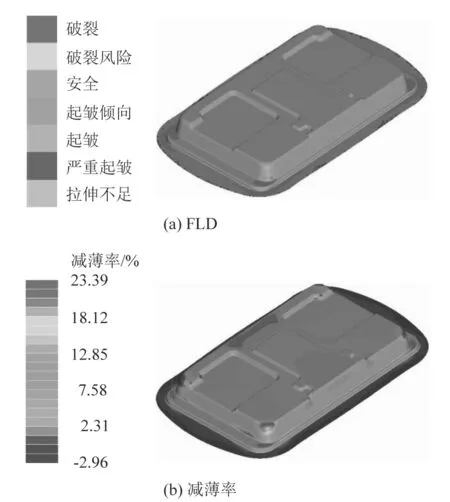
图6 优化后成形结果Figure 6 Optimized forming results

4 结语

1) 针对燃气灶外壳零件的厚度变化问题，课题组采用DYNAFORM6.0对其成形及优化过程进行有限元仿真。

2) 课题组利用RSM设计试验，分析几种工艺参数对燃气灶外壳零件最大减薄率和最大增厚率的影响规律。最大减薄率y1交互作用最显著的为A和B，随着压边力减小和圆角半径增大时，减薄率随之降低；最大增厚率y2的交互作用最显著的是B和C，y2随着压边力和模具间隙的增大而减小，并得到基于最大减薄率和最大增厚率多目标优化的响应目标函数y1和y2。

3) 课题组应用遗传算法设计NSGA-Ⅱ程序对响应目标函数建立多目标优化模型，得到Pareto多目标优化最优解集，选择合理优化工艺参数组合：圆角半径为13 mm；压边力为335 kN；模具间隙为0.84 mm。并通过仿真结果验证该试验方案的可靠性，为此类外壳零件的成形优化提供参考。