改进粒子群算法优化SVR水质预测模型研究
孟 滔
(四川大学锦城学院智能制造学院,四川 成都 611731)
引言
饮水安全越来越受到人们的关注。目前,我国农村在饮水安全上存在着众多的问题[1],随着越来越多的工厂建在农村,严重污染了农村的自然水源,导致大多数水源都受到了不同程度的污染。并且农村大多数自来水厂规模小,处理原水能力弱。目前农村自来水厂大多采用在线水质监测预警系统对原水和出厂水进行监测,但仅仅监测是不够的,需要对原水水质进行预测,提前知道原水水质情况,做好相应的应对措施,以降低自来水厂出厂水不达标的情况。
对于水质预测的方法,目前国内外采用主要有人工神经网络算法[2-4]、贝叶斯网络算法[5,6]、支持向量回归SVR算法[7]等。其中,SVR算法比人工神经网络算法、贝叶斯网络算法更适用于小样本数据,并且具有更好的泛化性,特别适用于规模较小的自来水厂进行原水水质预测。使用SVR进行原水水质预测时,需要先建立原水水质预测模型,其中核参数g和惩罚参数C是影响原水水质预测模型预测精度的关键。针对这2个参数,传统方法是使用网格搜索法进行参数寻优,但是其寻优时间特别长。针对这个问题,薛同来、赵冬晖等人[8]提出基于GA优化的SVR水质预测模型,该方法利用遗传算法对SVR的参数进行寻优,减少了参数寻优的时间;但由于SVR的最佳参数范围不定,当参数的寻优范围设置过大时,存在训练时间过长,当参数的寻优范围设置过小时,存在预测精度不高的情况。对于SVR参数寻优,柯声明[9]提出使用粒子群搜索方法优化SVR参数对CODMn进行预测,同样的由于SVR最佳参数范围不定,导致训练时间过长或者预测精度不高。
本文优化现有的粒子群搜索算法对SVR的核参数g和惩罚参数C的寻优范围。在一个较大的范围内通过网格搜索算法迅速得到一组最佳参数的粗值,根据得到的粗值减小粒子群搜索算法的寻优范围。实验表明,该改进算法比网格搜索算法、遗传算法、粒子群算法具有更短的训练时间,而且预测精度和网格搜索算法、遗传算法、粒子群算法相当。
1 支持向量回归SVR
支持向量回归SVR是支持向量机SVM中一个重要分支,用于解决预测问题。SVM是由Corters、Vapnik等人[10]在1995年提出的一种监督学习,适用于解决分类问题,后衍生用于解决数据回归预测问题。其核心思想是基于误差的结构风险最小化原则,在高维空间找出一条曲线来表示输入数据与输出数据之间的关系,通过该曲线的函数式就可以得到想要的预测值。该曲线函数可表示:
f(x)=wT·φ(x)+b
(1)
式中,w表示高维空间中的特征向量;φ(x)表示低维数据到高维空间的非线性映射。
对于公式(1)可构建公式(2)的代价函数:
(2)
式中,C表示惩罚参数,决定预测模型对数据的拟合程度。
对于公式(2)根据结构化风险最小原则和引入拉格朗日函数以及一些拉格朗日因子,得到最终水质预测的拟合函数表达式:
(3)
式中,K(xi,xj)是核函数,本文采用径向基核函数。
2 改进粒子群优化算法
粒子群算法(PSO)是基于对鸟类捕食行为的研究发展而来的,其基本思想是利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的最优解。将粒子群算法引入到SVR参数寻优当中,比传统的网格搜索算法具有更快的训练速度,并且当参数的寻优范围设置恰当时,其预测精度和网格搜索法基本相当。
2.1 传统粒子群算法
传统的粒子群算法对SVR参数的寻优范围往往是基于自身经验来进行设定的。如果参数的寻优范围设置过小,有可能会使得到的核参数g和惩罚参数C不是最佳的,影响预测精度。如果参数的寻优范围设置过大,那么就会存在寻优时间过长的问题。如何解决这个参数的设置范围是解决寻优时间过长的关键。
2.2 改进粒子群算法
通过传统网格搜索算法对某水厂耗氧量数据进行回归训练,结果如图1所示。

图1 网格搜索法寻优结果
从图1中可以看出,只有在比较小的范围内得到的均方误差MSE才是比较小的,所以如果可以在设置参数寻优时就得到此范围,那么使用粒子群算法时可以极大地缩短训练时间,并且得到的预测精度也不会降低。针对以上问题,可以使用传统网格搜索法在大范围内使用较大的步长对核参数g和惩罚参数C进行粗寻优,得到的一组最佳的粗值。然后通过适当放大和缩小该组粗值作为粒子群算法的参数寻优范围,该方法不仅可以减少建立SVR水质预测模型的时间而且不必对不同水质因子重新设置SVR参数的寻优范围,一样可以得到最佳的核参数g和惩罚参数C。在使用该方法得到核参数g和惩罚参数C较小范围内使用网格搜索算法进行回归训练,结果如图2所示,可以看出在比较大的范围内均方误差MSE都比较小。
改进粒子群算法具体实现如下:对水质数据进行预处理,异常和缺失数据使用单一插值法;对水质数据划分为训练数据和预测数据,并做归一化处理。
(4)
式中,xmin表示该列中的最小值;xmax表示该列中的最大值;y表示归一化后的数据。
设定惩罚参数C和核参数g在一个较大的范围。利用网格搜索法,初步求出(C,g)的粗值。此值作为粒子群算法参数C和g的基准值。根据得到的基准值放大和缩小2倍作为粒子群算法参数C和g的寻优范围。利用其建立的水质预测模型,对水质进行预测。

图2 优化后网格搜索法寻优结果
3 实验仿真结果分析
计算机平台为windows 10(64位)系统,处理器为i5-4210M,内存为16GB。使用软件仿真平台为matlab2010b,工具包采用使用较广泛的LIBSVM进行测试。SVR中核函数选用径向基核函数(RBF)。其中数据来自某自来水厂连续642组原水数据,该数据每天采集1次,包含4种水质因子数据:氨氮、耗氧量、浑浊度、总大肠菌群。其中,前635组数据作为训练数据,后7组数据作为预测数据。对这些数据分别采用网格搜索法、遗传算法(GA-SVR)、粒子群算法(PSO-SVR)、改进粒子群算法(IPSO-SVR)进行对比实验。
为保证全面对比各个算法的性能,实验中采用3种评价指标来说明算法的性能。第1个评价指标为均方根误差(Root Mean Squared Error,RMSE),定义为公式(5);第2个评价指标为平均相对误差(Mean Relative Error,MRE),定义为公式(6);第3个评价指标为最大相对误差(Biggest Relative Error,BRE),即相对误差的最大值。
(5)
(6)
4种算法对4种水质因子训练时间和预测性能如表1和表2所示。为保证实验的有效性,表中GA-SVR、PSO-SVR、IPSO-SVR实验结果取20次的平均值,网格搜索算法的实验结果取8次的平均值。

表1 训练时间
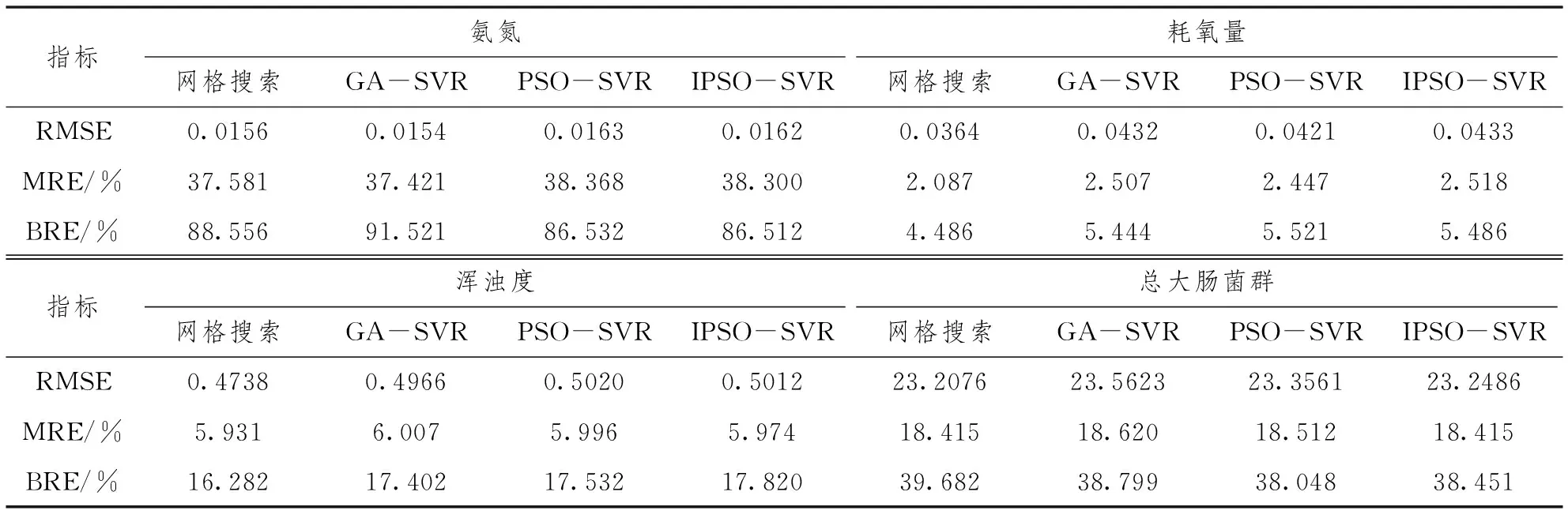
表2 4种方法预测性能
分析表1可知,对4种水质因子建立水质预测模型,网格搜索法建立水质预测模型花费的时间比其它3种算法都长,改进后的粒子群算法建立水质预测模型花费的时间最短。
这是因为网格搜索法需要对参数范围内的所有点进行计算,导致其寻找最佳参数组耗时最长。改进后的粒子群算法因为事先通过网格搜索法进行粗寻优后参数范围大大减小了,所以其寻找最佳参数组耗时最短。比网格搜索法时间最大大约缩短16.5倍,比遗传算法时间最大大约缩短6倍,比粒子群算法时间最大大约缩短1.4倍。
分析表2可知,对4种水质因子进行预测,4种方法的性能基本一致,这是因为在相同的参数寻优范围内,4种方法都能得到较好的参数组建立水质预测模型,这也说明了本文通过网格搜索法缩小参数寻优范围是可行的。
4 结论
针对使用粒子群算法建立SVR水质预测模型,其参数范围设置不确定,导致建立水质预测模型时间过长的问题。本文通过网格搜索算法缩小粒子群算法参数寻优范围,从而更快地建立水质预测模型。实验表明,使用该改进算法不仅可以有效地减少建立水质预测模型的时间,并且其预测精度和网格搜索法、遗传算法、粒子群算法相当。

