出行者对出行方式服务属性的感知差异研究

常四铁，严 飞，左 康

(武汉市规划研究院，湖北 武汉 430014)

0 引 言

随着我国社会经济持续快速发展，城市的机动化水平稳步提升。2017年，全国千人机动车拥有量达到156辆，近10年年均增长率约12%。机动化水平提升带来包括拥堵、停车、尾气排放、噪音污染等问题日渐突出。为缓解这一系列交通问题，有效降低私家车的出行比例，各地方政府纷纷实施了公共交通优先发展的战略，并加快公共交通线网和枢纽的建设。但是，实施效果始终未能达到预期，其本质是公共交通服务水平未能满足出行者需求。因此，亟需探究出行者出行方式选择行为，以支撑城市交通资源配置优化和公共交通运营服务水平提升。

既有研究表明，出行费用、行程时间及其可靠性、车内拥挤度是影响出行者方式选择的主要因素。相比于出行费用，行程时间、可靠性和车内拥挤度具有明显的不确定性。出行者一般基于主观感受对这两个因素做出判断，易造成主观感知的差异。感知差异性是指相同的服务属性水平对出行者选择效用产生差异化的影响[1]。在出行方式选择模型中忽略出行者对服务属性的感知差异会造成模型在需求预测中失准，导致公共交通资源错配。因此，有必要开展出行者对不同出行方式行程时间及其可靠性的感知差异性研究。

国内外对出行方式服务属性感知差异的研究已有一定基础。其中，以行程时间感知差异的研究成果最多，M.WARDMAN[2]、J.D.SHIRES等[3]、A.L.ABRANTES等[4]先后对相关研究进行了综述，均得出私家车出行的时间价值(value of time,Vt)显著高于公共交通出行Vt的结论。其次，邵敏华等[5]、L.HAYWOOD等[6]、A.TIRACHINI等[7]进一步探究了不同拥挤程度下，出行者对行程时间的感知差异，发现Vt随着拥挤程度增加而升高。丁月明等[8]、H.LI等[1,9]则分析了行程时间可靠性的感知差异，结果均表明轨道交通出行的可靠性价值(value of reliability,Vr)显著高于其他方式出行的Vr。

聚焦出行者对私家车、地铁、常规公交的行程时间及其可靠性、车内拥挤度的感知差异研究，基于上海市居民出行意愿(stated preference, SP)调查，建立考虑行程时间与车内拥挤度交叉项的出行方式选择行为模型；根据模型通用参数(generic parameters)估计结果，研究不同车内拥挤程度下的行程时间感知差异；并通过选项特定参数(mode-specific parameters)的估计，揭示出行者对不同出行方式的行程时间、可靠性的感知差异。

1 数据采集

以上海市为例，通过SP调查获取出行者在不同情景下的选择行为数据。在SP问卷中，受访者被要求在假设情景中选择合适的出行方式，备选方案包括私家车出行、地铁出行、常规公交出行3种常用的通勤交通方式。每一种被选方案中考虑出行费用、行程时间、可靠性及车内拥挤度4个影响因素。其中，私家车出行的费用主要包括燃油费、停车费和过路过桥费；其余两种出行方式的费用为票面价格。车内拥挤程度分为不拥挤有座(S)、拥挤有座(Cs)和拥挤无座(Cns)。对不同出行方式的各影响因素分别设置3个变化水平，以供受访者权衡决策，水平设置情况汇总如表1。

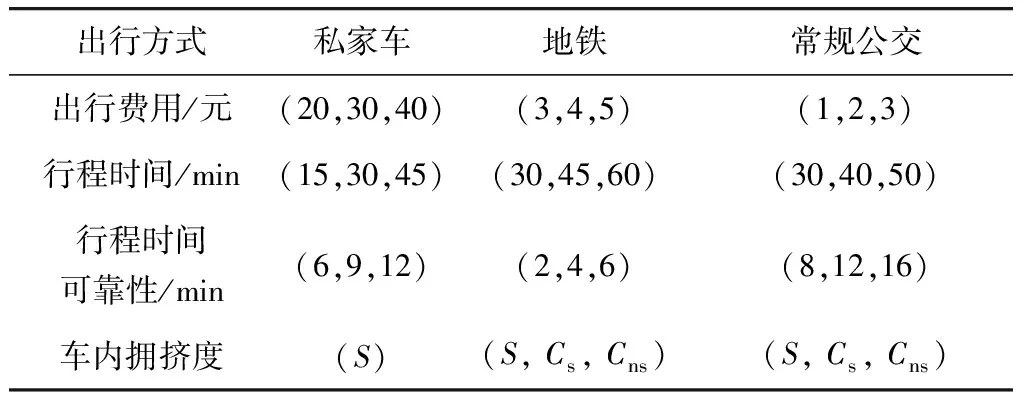
表1 SP情景的影响因素及其水平设置情况

行程时间及其可靠性分别被定义为行程时间分布的平均值μ和标准差σ。在实际调查过程中，考虑到受访者可能缺乏相关的数理统计知识，故采用向受访者展示4组行程时间范围及其发生的可能性，使其分辨备选方案行程时间可靠性的形式。为方便4组行程时间范围的设置，假设行程时间服从正态分布，设置4组行程时间范围分别为：≤(μ-σ)、(μ-σ)～μ、μ～(μ+σ)、>(μ+σ)。根据正态分布的统计特性，这4组时间范围发生的可能性分别为16%、34%、34%、16%。以地铁出行，行程时间30 min，行程时间可靠性6 min为例，SP情景中的展示如图1。

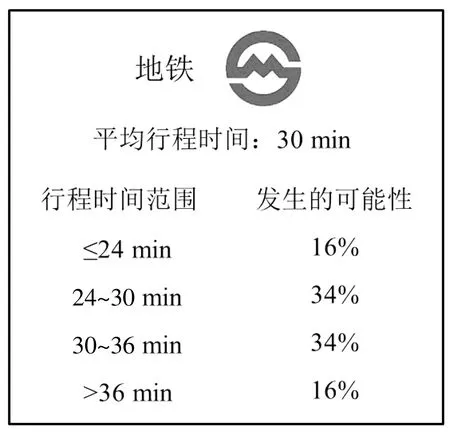
图1 SP场景中行程时间及其可靠性展示

根据表1中的影响因素及其水平设置，采用软件Ngene，基于D-efficient设计实现每个场景中各个选项因素水平的组合。为将每位受访者的问卷填写时间控制在5～10 min，每张问卷中假设情景的数量设为9个。课题组于2018年10月11—13日采用随机抽样对上海市居民开展为期3天的问卷调查。调查内容除SP情景选择外，还包括年龄、性别、年收入、私家车拥有情况等基本信息。调查最终回收462份问卷，其中有效问卷366份，共3 294组假设情景，其余问卷均有不同程度的内容缺失。有效样本数据的基本统计如表2。

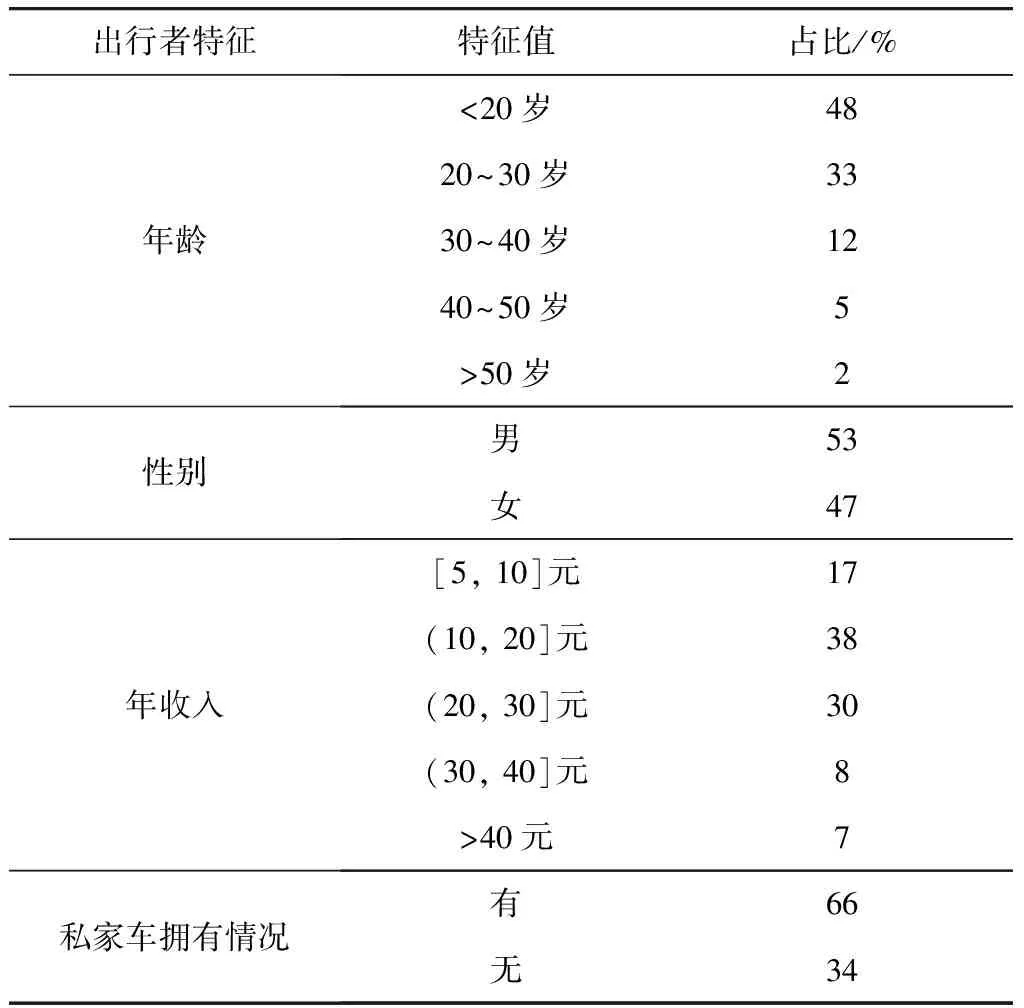
表2 样本数据基本统计情况

2 模型构建

2.1 模型理论

以基于随机效用最大化(random utility maximiza-tion, RUM)的离散选择模型为主要分析工具，研究出行者选择行为特征。RUM理论从微观经济学的理性假设出发，认为出行者面对效用具有差异性的备选出行方式时，会根据认知选择能够最大程度满足其需求的方案。基于此，假设出行者n的备选出行方式集合为An，出行方式i对出行者n的效用为Ui,n，则出行者n选择出行方式i的条件为：

Ui,n>Uj,n(∀i≠j∈An)

(1)

Ui,n可以表示为可观测的确定项Vi,n和不可观测的随机项εi,n之和：

Ui,n=Vi,n+εi,n

(2)

基于式(2)中不可观测项εi,n服从二重指数分布的假设即推导得到Logit模型。Logit模型包括MNL(multinomial logit)模型和ML(mixed logit)模型等。其中，MNL模型的应用最为广泛，其优点在于模型结构简单，参数估计方法成熟。MNL模型假设各备选方案的不可观测项εi,n服从独立同分布，故具有各备选方案独立不相关(independence of irrelevant alternatives, IIA)特性，无法刻画备选方案之间的关联性。ML模型假设变量参数为服从某一特定分布的随机参数来捕捉被调查者之间的异质性，且放松了不可观测项εi,n独立同分布的假设，因而能够有效克服MNL模型的IIA特性。

计算出行者为改善服务水平的支付意愿是Logit模型的主要应用之一。其中，出行者为缩短一单位行程时间和提高一单位可靠性的支付意愿分别称为Vt和Vr。Vt和Vr是评估基础设施建设、交通政策实施和服务水平提升等收益的重要参数，两个指标的计算公式分别为：

(3)

(4)

式中：C、T、R分别为费用、行程时间和可靠性。

2.2 效用函数构建

当前，离散选择模型中最常用的效用形式为LPLA(linear in the parameters, linear in the attributes)形式。LPLA形式假设各解释变量对选择效用的影响是相互独立的。但实际情况中，一个变量对选择效用的影响可能取决于另一个变量水平，即这两个变量对选择效用的影响表现为交互影响。引入交叉项的效用形式能够弥补LPLA形式无法解释变量交互影响的不足[10]。既有研究表明，出行者对行程时间的感知受车内拥挤程度的影响。因此，有必要引入车内拥挤度与行程时间的交叉项(即式(5)中的Csi,n×Ti,n和Cnsi,n×Tin)，以探究不同拥挤程度下，出行者对行程时间感知的差异。最终，效用函数构建如下：

Vi,n=αi+βi,c×Ci,n+(βi,t+βi,cs×Csi,n+βi,cns×Cnsi,n)×Ti,n+βi,r×Ri,n

(5)

式中：Ci,n、Ti,n、Ri,n、αi分别为出行方式i(i=1,2,3分别为私家车出行、地铁出行和常规公交出行)的费用、时间、可靠性和常数项。Cs、Cns均为车内拥挤度的虚拟变量：当车内拥挤程度为拥挤有座时，Cs=1，否则Cs=0；当车内拥挤程度为拥挤无座时，Cns=1，否则Cns=0；当车内拥挤程度为不拥挤时，Cs=Cns=0。βi,c、βi,t、βi,cs、βi,cns、βi,r分别为相应的待估计系数。

分别采用MNL模型和ML模型对上述效用函数进行参数估计，并且将MNL模型的参数估计结果设置为ML模型的初始默认值，从而提高ML模型的参数估计精度和减少估计的运行时间[11]。进行ML模型参数估计时，先将效用中涉及的参数均设为随机参数，随机参数假设服从正态分布。根据模型的估计结果，判断随机参数标准差的T-检验值是否大于在90%置信水平下的临界值(1.64)。并将标准差的T-检验值小于1.64的参数逐一退化为固定参数。模型参数估计均采用Nlogit 5专业软件。下一节中将针对模型参数估计结果进行分析。

3 结果分析

通用参数是指不区分不同出行方式同一变量的待估计参数，其估计结果能够反映出行者对出行方式服务属性的平均支付意愿。选项特定参数是指区分不同出行方式的同一变量的待估计参数，其显著性估计结果体现出行者对不同出行方式同一服务属性变量的感知差异。

首先对构建的效用函数进行通用参数估计，从整体上分析出行者Vt和Vr的平均水平以及不同拥挤条件下的Vt差异。在此基础上，区分不同出行方式的行程时间和可靠性的待估计参数，解析出行者对不同出行方式中这两个变量的感知差异。

3.1 通用参数估计

基于MNL模型和ML模型的通用参数估计结果如表3。

从表3可知，MNL模型和ML模型的McFadden系数均大于0.2，表明两类模型均能较好的解释出行者出行方式的选择行为。其次，似然比检验结果显示ML模型显著优于MNL模型，即似然比指标值(-2×(LL(β)ML-LL(β)MNL)=4.36)远大于自由度为2的卡方分布在95%置信水平下的临界值(0.103)[10]。因此，笔者将采用ML模型的估计结果进一步分析出行者的Vr/Vt，并量化不同车内拥挤程度下的行程时间感知差异。

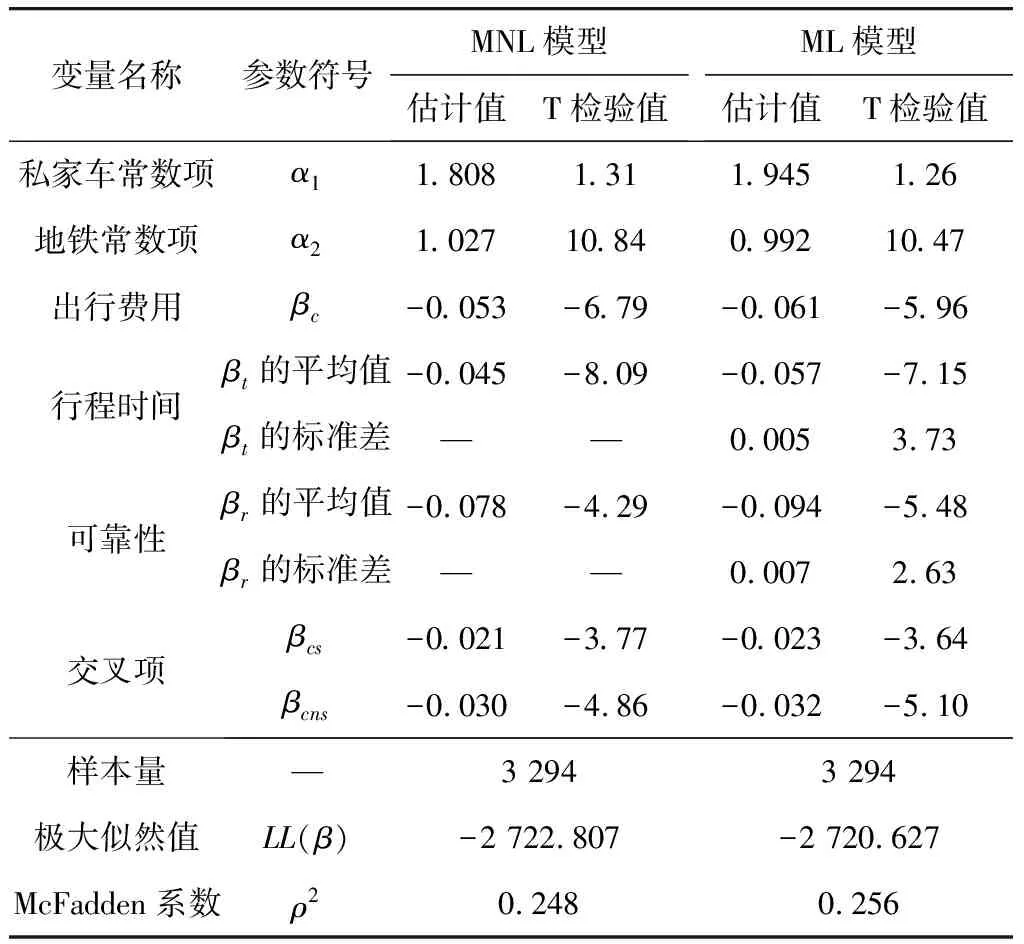
表3 通用参数估计结果

从参数估计结果可知，车内拥挤度变量(Cs和Cns)与行程时间的交叉项显著，表明出行者在不同车内拥挤程度下对行程时间的感知存在显著差异。这一差异可用不同车内拥挤程度下的Vt比值进行量化。根据Vt的计算公式，车内拥挤程度为S、Cs、Cns时的Vt分别为56.1、78.9、87.5元/h，即车内拥挤程度为Cs时的Vt是车内拥挤程度为S时Vt的1.41倍，车内拥挤程度为Cns时的Vt是车内拥挤程度为S时Vt的1.56倍。而出行者Vr为92.5元/h，Vr与不同车内拥挤程度下的Vt的比值分别为1.65、1.17、1.06。这一结果符合文献[12]得出的Vr与Vt的比值在0.7～2.0范围的结论。其次，Vr与Vt的比值均大于1，说明相比于行程时间，出行者在出行方式选择时更加重视行程时间的可靠性。

3.2 选项特定参数估计

基于MNL模型和ML模型的选项特定参数估计结果如表4。

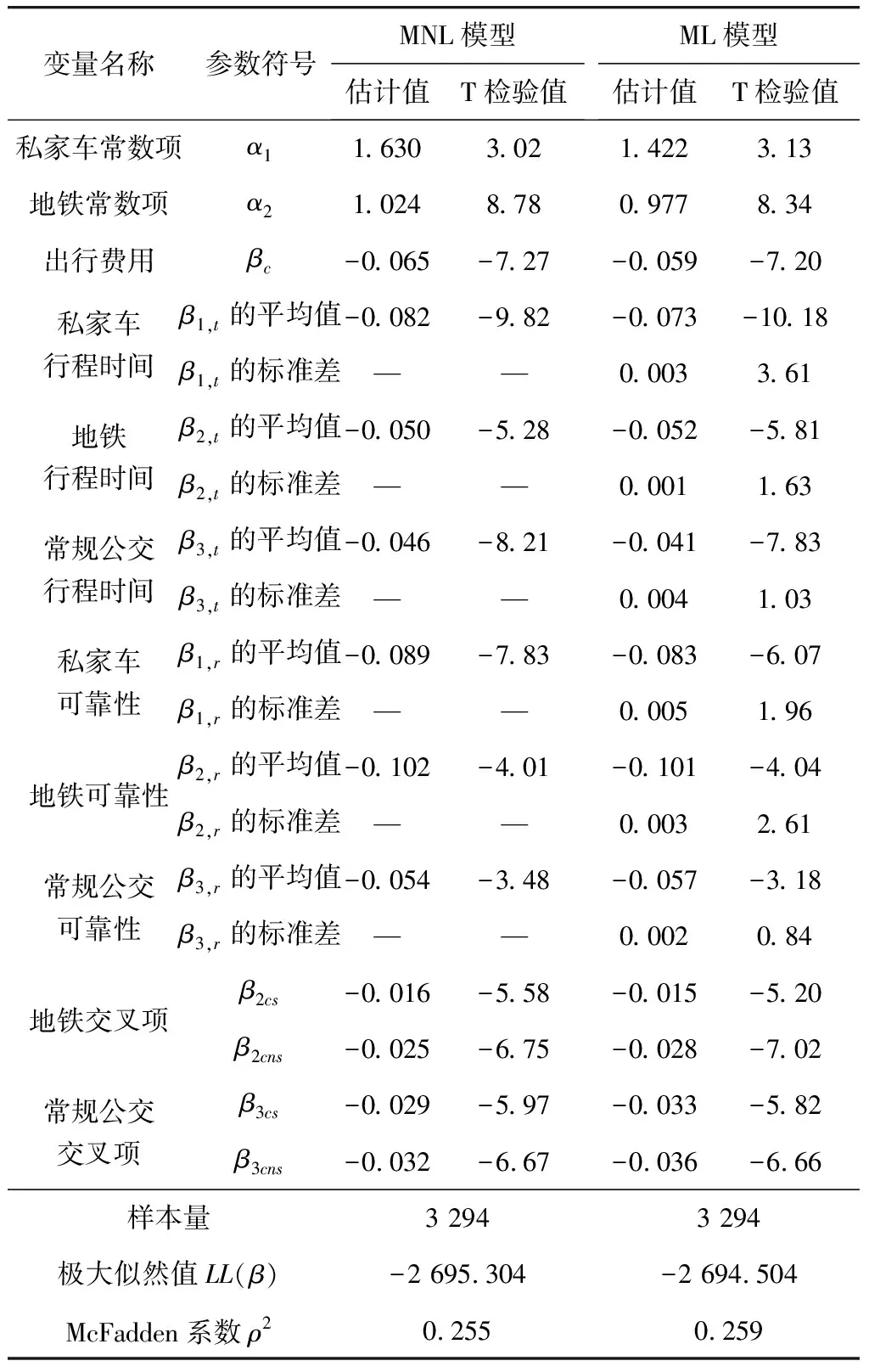
表4 选项特定参数估计结果

从表4可知，ML模型与MNL模型的似然比指标值：-2×[LL(β)ML-LL(β)MNL]=1.60，小于自由度为6的卡方分布在95%置信水平下的临界值(1.635)。因此，未能有效证明ML模型显著优于MNL模型，笔者将采用MNL模型的估计结果分析出行者对不同出行方式行程时间和可靠性的感知差异。

根据选项特定参数估计，基于式(3)、式(4)，得到基于选项特定参数估计的Vt和Vr测算结果，如表5。表5中结果显示，私家车出行、地铁出行和常规公交出行的Vr分别为82.2、94.2、49.8元/h。这一结果表明，出行者对不同出行方式行程时间可靠性存在显著的感知差异性，具体表现为，同样的可靠性水平对出行者选择地铁产生的负效用影响大于私家车出行和常规公交出行。这可能是由于，当前地铁出行的行程时间可靠性优于其他两种出行方式，故出行者对地铁出行的可靠性水平具有较高要求，而当可靠性水平未能达到其预期时，将大大提升出行者选择地铁出行的负效用。

表5 基于选项特定参数估计结果WTP测算

当车内拥挤程度为S时，私家车出行、地铁出行和常规公交出行的Vt分别为75.7、46.2、42.5元/h，说明私家车出行的Vt远高于地铁出行和常规公交出行。而当车内拥挤程度为Cs时，地铁出行和常规公交出行的Vt分别为60.9、69.2元/h；当车内拥挤程度为Cns时，地铁出行和常规公交出行的Vt分别为69.2、72.0元/h。这些结果表明：在拥挤情况下，常规公交出行的Vt大于地铁出行，即在拥挤时，相比于常规公交，出行者更倾向于选择地铁出行。因此，结果显示了出行者对不同出行方式行程时间存在显著的感知差异性

4 结 语

基于上海市居民出行意愿调查，采用离散选择理论探究出行者对私家车、地铁、常规公交的行程时间及其可靠性、车内拥挤度的感知差异，主要结论包括：在不同车内拥挤程度下，出行者对同一出行方式行程时间的感知存在显著差异，表现为车内拥挤有座时的Vt是车内不拥挤有座时Vr的1.41倍，车内拥挤无座时的Vt是车内不拥挤有座Vt的1.56倍；相比于行程时间，出行者在出行方式选择时更加重视行程时间的可靠性，说明改善公共交通的行程可靠性相对于减少行程时间能够更有效吸引出行者使用公共交通；出行者对不同出行方式行程时间可靠性存在显著的感知差异性，家车出行、地铁出行和常规公交出行的Vr分别为82.2、94.2、49.8元/h，说明同样的可靠性水平对出行者选择地铁产生的负效用影响远大于私家车出行和常规公交出行；同一车内拥挤程度水平下，常规公交出行的Vt大于地铁出行，即相同的车内拥挤程度时，相比于常规公交，出行者更倾向于选择地铁出行。