因素空间理论下银行信用卡违约预测

刘晓同，曾繁慧，刘晓娟

（1. 辽宁工程技术大学 理学院，辽宁 阜新 123000；2. 辽宁工程技术大学 智能工程与数学研究院，辽宁 阜新 123000； 3. 阜新市产业技术研究院 高学历人才管理部，辽宁 阜新 123000）

0 引言

近年来，中国许多商业银行在信用卡应用中采用了数据挖掘技术，并在预测模型的开发中使用了许多工具，例如线性回归分析、神经网络、支持向量机、决策树和其他数据挖掘方法[1-3].在这个信息多样化的时代，金融行业及其他各个领域的信息和数据量急剧增加，基于因素库的知识发现和知识约减是从海量数据中提取有效信息的重要方法[4-6].因素空间是智能信息处理的一个重要数学理论，为知识表示提供数学框架.世界上的一切事物都不能与因素分开，事物之间的比较和划分也离不开因素.因素空间作为信息描述的基本数学框架，是信息的载体和信息统计分析的基础，该理论成为数据科学的理论基础.崔铁军[7-8]将汪培庄提出的逆向逻辑归纳思想应用于空间故障树理论的研究.本文将对这一思想作出更明确的数学描述，同时，引入背景分布和模糊背景关系，提出逆向因果分析逻辑算法，并将其应用于银行卡的信用分析，创建基于逆向因果分析法的银行信用卡违约预测模型，对评定用户的信贷风险、推动中国金融业销售市场平稳发展有一定实际意义.

1 预备知识

1.1 因素空间

1.2 因果分析

定义3 给定因果空间，称（D，F={f1, …,fn;g}）为因果分析.见表1，行表示论域，第2列表示条件因素.最后一列为结果因素，第i行第j列元素是第i个对象在第j个因素下的值态.

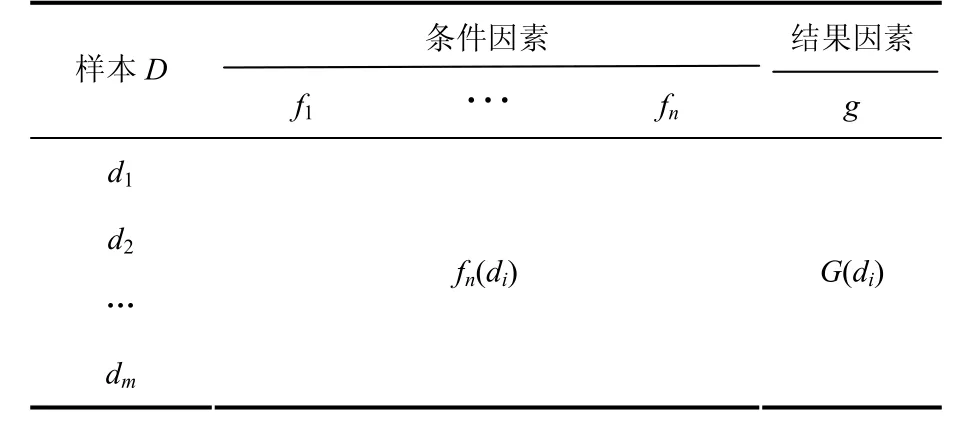
表1 因果分析 Tab.1 causal analysis

1.3 决定度

1.4 因素空间的背景分布

2 逆向因果分析逻辑算法

2.1 算法原理

在因素空间的理论下，各因素之间的联系变得更加密切，因素之间的联系方式成为探求目标，因果分析就是探求因素之间联系的重要手段之一，有两种不同的方向，一个是从因到果的正向因果分析，另一个是从果到因的逆向因果分析.本文采用逆向的角度来分析因果之间的联系，建立逆向因果树.

逆向因果分析的主要过程分为以下个步骤.

步骤1从结果出发，用结果进行分类，每一类按照因果分析表对条件进行组合，形成一一对应的因果句，将同一类的因果句连接起来形成析取范式，通过逻辑化简求得最小式即为因果之间的推理规则.

步骤2根据样本类求得每一句因果句的概率分布，因果句的概率分布影响该因果句产生的规则的强弱.

步骤3利用求得的最小式转换成因果推理规则，根据各因素的决定度建立因果反向树.

2.2 基本算法

如何快速提取逆向因果分析法的推理句，步骤如下.

输入 因果分析表U,F,G；

输出 推理句L.

（1）置原始分类C: =[U],条件因素F: = {f1,f2,… ,fn}和结果因素I(g)={G1=真，G2=假}，G: = {G1，G2}，规则集L:=∅，称q: = {q1,q2,… ,qn}为每个条件因素的类别个数.

I=I(f1) + … +I(fn) (+表示不交并)称为字集.对每个单字，若不在假的所有属性组合中出现，则由该字必可推出真.在检查由两个字所组成的字组，若不在假集中的所有项中出现，则由此两字的合取，必可推出真.

若 xa⊆ L[ Hi]，则xa→ga= G .

3 逆向因果分析信用卡违约预测模型

3.1 数据重构与分析

（1）数据说明

数据集来源于UCI网站，共有30 000个信用卡用条记录户，其包含了23个描述用户特征的条件因素，1个为次月违约情况的结果因素，其值态分为：“0”为履约和“1”为违约，见表2.

针对比较集中的数据进行清理和预处理.例如，如果教育水平是5、6，则是异常数据，需要在建模期间消除.异常检测方法可以通过绘制数据集的箱形图来完成.处理方法通常可以包含以下方法：① 若处于正常状态下的数据，则以保留；② 若数据是离群点，建立模型时需要删掉；③ 在对数据进行整理重构时，可应用中位值或是平均值更换.

表2 信用卡用户样本数据集的因素描述 Tab.2 factor description of credit card user sample data set

（2）因素的统计性分析

首先将数据进行清洗和重构，利用统计学相关知识对原始数据集做一个初步了解和分析.选取部分条件因素进行描述性统计分析.图1展示了信用卡客户性别分布情况，从中可以得到，包含约60%的女性客户，40%的男性客户，男女比例为3 2∶，并且没有其他异常值出现.

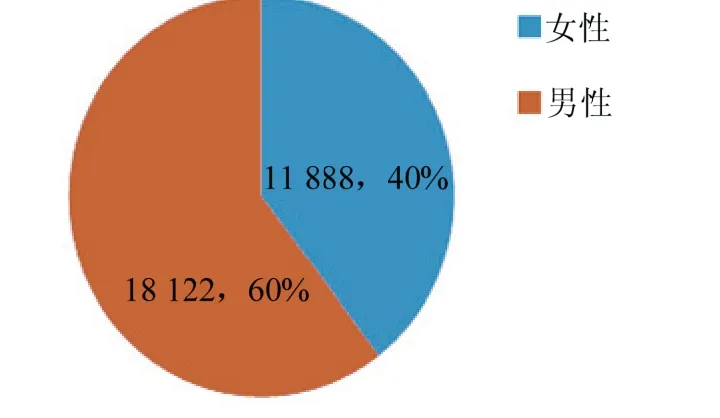
图1 信用卡用户性别分布情况 Fig.1 gender distribution of credit card users

图2 是信用卡客户教育程度情况，大部分信用卡客户的学历都集中在高校，拥有大学本科及本科以上学历的客户占绝大部分.拥有硕士研究生及以上学历的用户数要显著高于高中文凭及以下的用户数.

图2 教育水平分布 Fig.2 distribution of education level

如图3，信用卡客户配婚状况非常复杂，图中显示信息的仅是客户申请信用卡时填写的配婚信息，单身客户超过了己婚和其他用户总数.

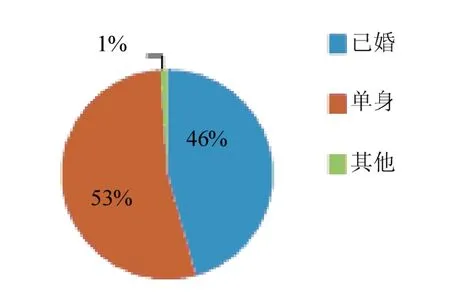
图3 婚配统计 Fig.3 marriage statistics

见图4，信用卡用户的年龄分布状况，在20岁和50岁中间的群体达到总人数的约 80%.根据世界卫生组织对于年龄段的划分标准，18岁至45岁为青年，46岁至59岁为中年人，60岁以上为老年人.因此青年客户显著超过中年人和老年人客户.随着年龄的上升，用户数逐渐呈下降趋势.从现实情况来看，这也是符合常规的数据分布状况.

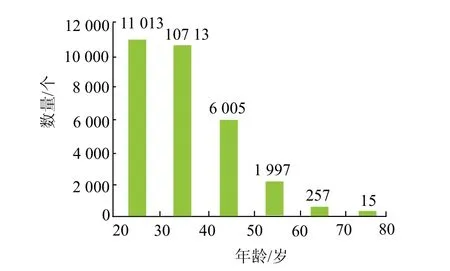
图4 年龄分布 Fig.4 age distribution

图5 为10个标值型因素的描述性统计结果，从折线统计图能够看出，每个月月度账单结算金额平均值相对较为轻缓且处于逐渐增长的趋势，表明越来越多的人在使用信用卡.

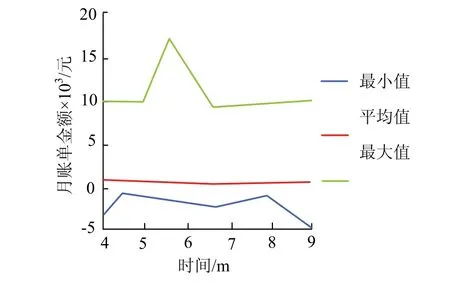
图5 2005年4月-2005年9月月度账单结算金额 Fig.5 monthly bill settlement amount from April 2005 to September 2005

如图6，每个月的月度支付金额则处于5 000台币左右，与月度账单结算金额差别极大，表明有一部分客户选择了分期还款或是有延期还款情况.

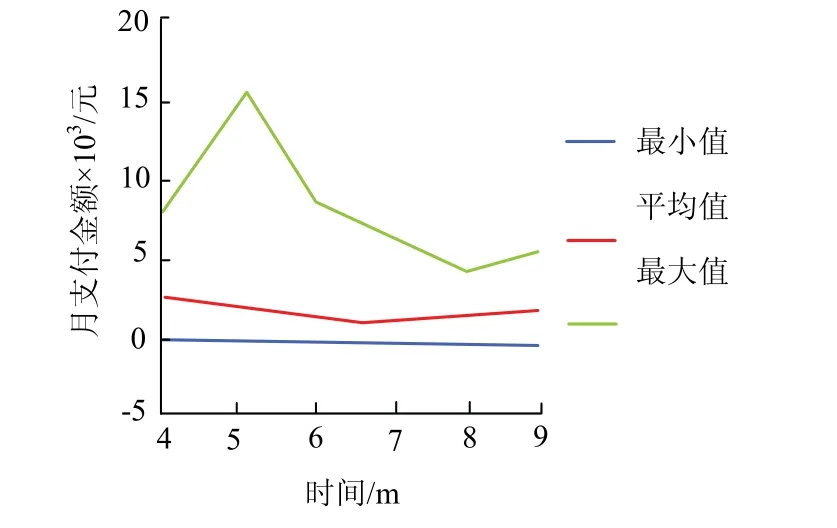
图6 2005年4月-2005年9月度支付金额 Fig.6 monthly payment amount from April 2005 to September 2005

（3）因素的相关性分析

利用R语言软件中的相关程序得到各个条件因素之间的相关性，同时对因素相关性分析结果做可视化处理，见表3，每个条件因素和其他因素均具有关联性信息内容，而每一个因素和它自身因为具备明确关联性，所以和本身关联性的研究并无实际意义.

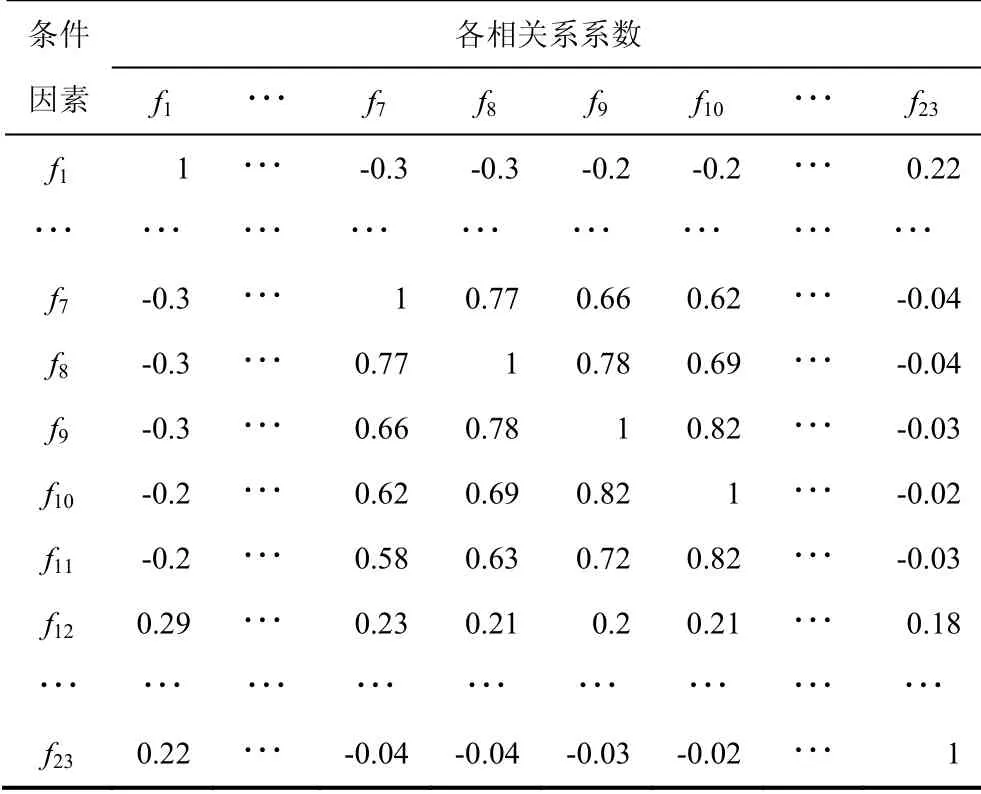
表3 相关系数 Tab.3 correlation coefficient

图7中f1到f23分别代表：信用卡额度、性别、教育程度、婚姻状况、年龄、2005年4月至2005年9月还款情况.f6到f11分别表示2005年4月至2005年9月度账单结算金额，f12～f17分别表示2005年4月至2005年9月月度支付金额，f18～f23分别表示2005年4月～2005年9月月度支付金额.通过研究相关系数矩阵可以发现存在高度相关的变量，其中2005年9月度支付金额与2005年4月、2005年5月、2005年6月、2005年7月、2005年8月月度支付金额之间的相关系数为分别为0.8、0.83、0.86、0.89、0.95，呈现高度相关，因此将后两者剔除，只保留2005年9月度支付金额宏观因素.

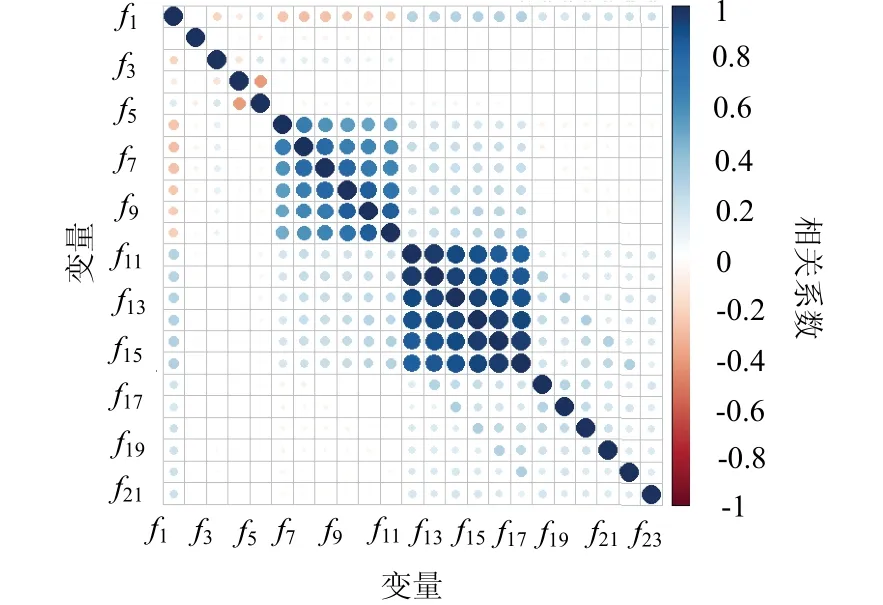
图7 变量之间的相关性 Fig.7 correlation between variables

图7应用不一样的色调表明了关联性的高低水平，参照图形右边的色调带，越贴近鲜红色，因素之间的关联性越低，而反过来的越贴近深蓝色表明关联性水平越高.图7中渲染色调的部分区域的大小还可以体现关联性的强弱.

通过以上方式，本文筛选出了所有相关系数较高的因素组合，保证因果分析表中各个条件因素相互之间具有一定的相对独立性.

（4）因素离散化处理

为了便于逆向因果分析法的应用，需要对条件因素做相应的离散化处理，或采用分段函数的形式对数据的不同分布区度进行定性处理.本文选取以下6个影响因素进行研究：信用卡额度、教育水平、年龄、还款情况、账单、支付金额.每个影响因素有不同的特征表现，为研究方便，本文依据现有的数据，结合逆向因果分析法，进行因素的离散化处理.

① 信用卡额度

信用卡额度f1是按照银行给定用户的信贷金额大小划分的类型.根据文中数据不同的分布区度，采用分段函数的方式进行处理，可划分为三个类，即

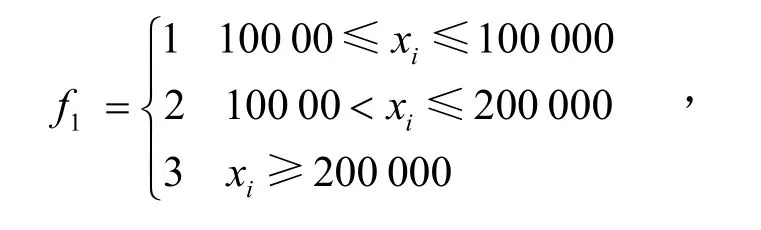
式中，当f1为1时，信用卡额度低；当f1为2时，时，信用卡额度低中；当f1为3时，为信用卡额度低高.

② 教育水平

教育水平f2是指信用卡用户的教育程度，研究生及以上为1；本科生为2；高中及以下为3.

③ 年龄

年龄f3将不同信用卡用户人群按年龄分段，老年为1；中年为2；青年为3.

④ 还款情况

还款情况f4是指持卡人1个月的付款历史，1为好；中为2；差为3.

⑤ 账单

账单f5为月度帐单金额，好为1；中为2；差为3.

⑥ 支付金额

支付金额f6为6个月月均支付金额，差为1；中为2；好为3.

⑦ 是否违约

其中是否违约g取值为0或1，履约为0；违约为1.

按上述数据离散化定性处理规划，得到因果分析法背景样本见表4，频率等同于因素空间里的背景分布，表示该样本在论域内出现的次数与样本总数的比值.

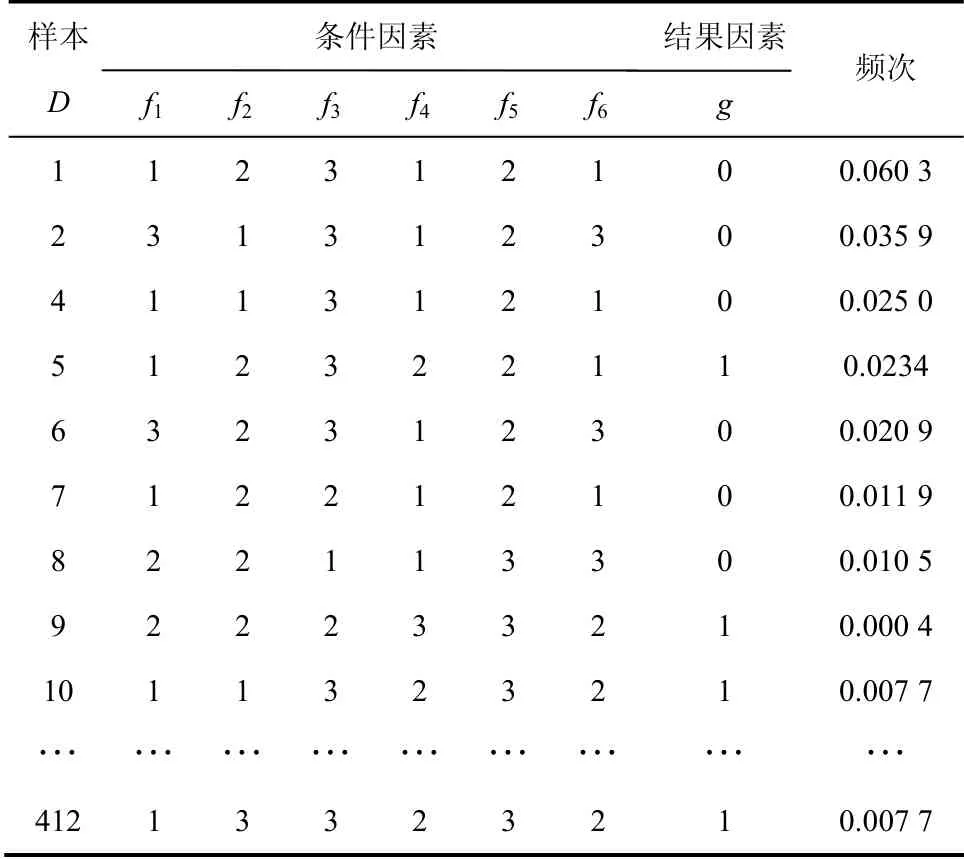
表4 信用卡数据的因果分析 Tab.4 causal analysis of credit card data

因果分析表包括6个条件因素和一个结果因素，每个条件因素有3个取值，因此共有36×2=1 458种样本类，而在原始29 963 条记录中有412种样本类可使用，进而得到背景分布.其中违约用户共106人，履约客户共306人.用样本类构造因果分析表才能使预测的结果更贴近实际情况，使算法更具备实际应用价值.

3.2 实验结果分析

针对因素空间理论在连续型数据集适用性问题，结合数据离散化方法利用因素空间理论下逆向因果分析法，选取信用卡额度、教育水平等6个指标作为条件因素，将是否违约作为结果因素，建立基于因素空间的银行信用卡违约预测模型.根据已知样本数据变量特征，利用逆向因果分析法产生的推理规则，对待测样本进行银行信用卡违约预测，并与真实情况进行比较，概率由表4的频次测算出来，代表预测结果的正确与否的程度，见表5.

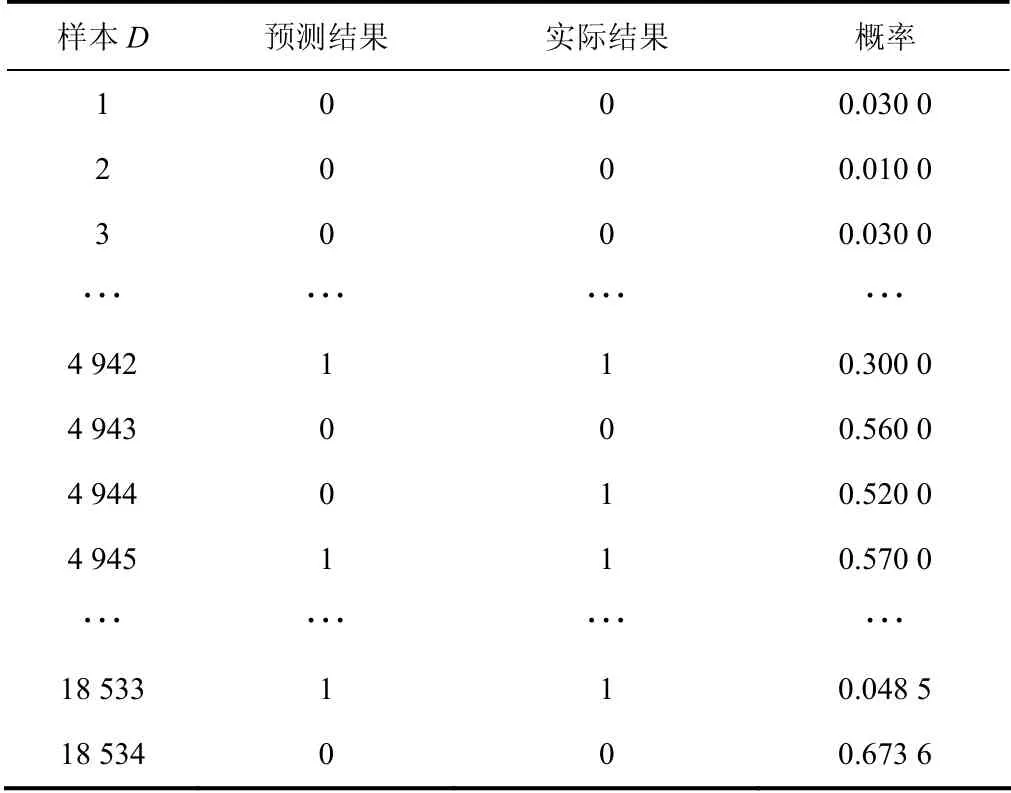
表5 银行信用卡违约预测结果 Tab.5 bank credit card default prediction results

3.3 模型评价

（1）评价指标

为验证所建模型的准确性，必须采用合理的评价方法，并且针对不同类型的模型，采用不同的评价方法.

选用混淆矩阵和依据混淆矩阵衍化出的3个指标值来进行模型的评价，分别为履约分类准确率（Accuracy _P）、违约分类准确率（Accuracy _D）、整体分类准确率（Accuracy）.

在各种机器学习算法中，混淆矩阵，也可以被称作误差矩阵，作为一种呈现模型特性的数据分析工具，非常适用监督学习，是评价指标体系精度的一种规范格式，通过构建一个方阵，将预测分析的分类结果和具体分类结果同时展现出来.文中的混淆矩阵为一个2×2的矩阵，其中，行：实际的分类类别样本数目，列：预测的分类类别样本数目，见表6.

表6 混淆矩阵 Tab. 6 confusion matrix

各评价指标的计算公式为

（2）银行信用卡违约预测模型

在逆向因果分析逻辑算法中，选取的条件因素的个数会影响分类的结果，规则的普适度关键取决于训练样本的完备性，样本类能够反映覆盖母体整体样本的水平.依据因素空间中以背景关系为母体的样本理论，逆向因果分析法的逻辑推理方式具备普遍意义.经计算，得到逆向因果分析法的混淆矩阵见表7.

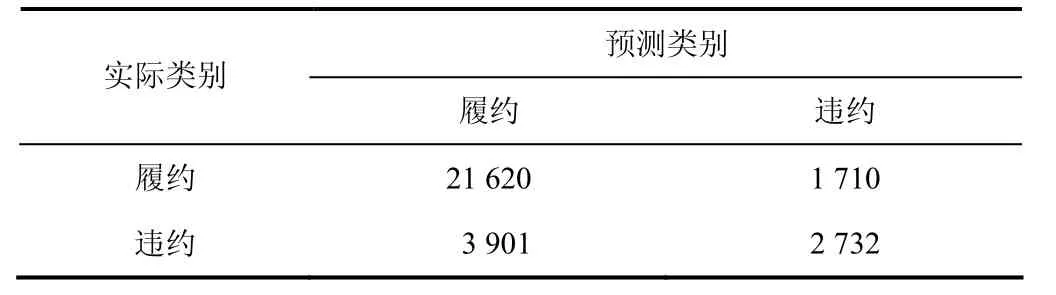
表7 逆向因果分析法的混淆矩阵 Tab.7 confounding matrix of reverse causality analysis

由表7得到Accuracy _P为92.670 4%、Accuracy _D为41.188 0%、Accuracy为81.300 0%.基于逆向因果分析法的银行信用卡违约预测模型对于整体的分类准确率与履约类别的分类准确率较高，相比之下，对于违约类别的分类准确率较低.

（3）模型比较

基于一个信用卡实际数据集，将经过预处理的数据读取到Matlab的工作空间中，应用正向因果分析法、决策树和逆向因果分析法分别结合样本数据建立了分类模型.通过对比表8中各模型的预测结果，可知逆向因果分析法的分类准确率整体上要高于决策树和正向因果分析法.

从履约类别由高到低排序为：逆向因果分析法，正向因果分析法，决策树.

从违约类别由高到低排序为：决策树，逆向因果分析法，正向因果分析法.

因此，实际应用表明，逆向因果分析法预测信用卡用户违约具有一定可行性.且在一定程度上分类的准确率要高于其他两种方法.

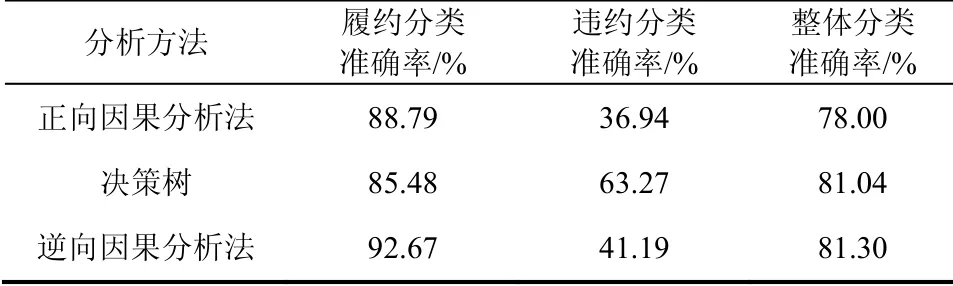
表8 模型比较 Tab.8 model comparison

4 结论

（1）将因素空间中的逆向因果分析法引入银行信用卡违约预测，引入背景分布计算各因果句的概率分布，能够较好地利用信用卡用户的实测数据，防止预测分析中主观性强的缺陷.该预测方法具备较好的自适应性，算法简单易行.

（2）模型的实证分析采用混淆矩阵和若干分类准确度相关评价指标来完成.预测结果表明，基于因素空间的银行信用卡违约预测方法能得到更加准确的违约预测结果和更完全的因果推理规则.