层次分析法在电池供应商评价体系的应用

陈汉武，陈欣麟，窦贤云，谢远锋

（1. 泛亚汽车技术中心有限公司，上海 浦东 200120；2. 湖北省蓄电池产品质量监督检验中心，湖北 襄阳 441000）

0 引言

供应链管理的思想从上世纪 90 年代传入中国以来，便受到各个企业的普遍关注。供应商管理则是供应链管理中一个很重要的环节。当今社会经济的迅猛发展，客户需求的多变，使得供应商的评价与选择成了供应商管理的热点话题。对于制造企业来说，只有挑选出符合企业自身发展战略要求的供应商，才能保证企业在残酷的市场竞争中实现长足发展。

起动用铅酸蓄电池的选型需要考虑的因素很多，一般由发动机类型、排量、气候因素和车载电器的多少来确定，而起动机的功率是选择蓄电池的主要因素。笔者不考虑选型中的因素，而是在市场上购买甲、乙、丙、丁四家供应商的电池，根据国家标准进行检测，通过国家标准中的测试数据对电池的性能做客观评价，选取性价比最高的供应商。选择的 4 个厂家的产品质量水平很接近，在国内都属于一线品牌，所以电池的性能相差不是很悬殊，只是各有偏重。这给评价方法的选择带来很大的难度，很难用“好”、“较好”、“一般”、“差”、“较差”常规的五分制原则确定各等级。因此，笔者采用层次分析法作为该项目的基本评价方法。

1 层次分析法建立综合评价数学模型的建立

层次分析法（AHP）是运筹学家 T. L. Satty 等人提出一种定量与定性相结合的综合评价方法。具体来讲，就是将与决策有关的因素分解成若干个层次，一般来讲分为方案层、准则层和目标层，并在进行定量和定性分析的决策方法。其基本思想就是把复杂问题分解为若干层次，由低层次通过成对比较法确定各目标权重，再通过对上一层的因素排序得出权值，最后进行层次总排序，确定优选次序列，作为决策依据。

1.1 明确问题

首先对问题要有明确的认识，弄清问题的所包含的范围、因素及因素之间的相互关系、需要得到的解答，通过对系统的深刻认识，确定该系统的总目标。

1.2 建立层次结构

按目标的不同、实现功能的差异，将系统分为几个等级层次，如目标层、准则层、方案层等，用框图的形式说明层次的递阶结构与因素的从属关系（参见图 1）。当某个层次包含的因素较多时，可将该层次进一步划分为若干子层次。层次分析模型是层次分析法赖以建立的基础，是层次分析法的第一个基本特征[1]。

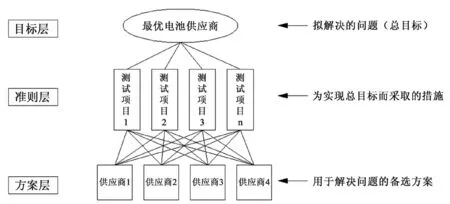
图1 层次结构示意图

1.3 构造判断矩阵

层次分析模型建立之后，每一层次中各因素相对重要性需要给出判断，在各层元素中进行两两比较，构造出比较判断矩阵。通常采用 1 – 9 标度及其倒数的标度方法，引入合适的标度用数值表示出来，写出判断矩阵，使决策判断定量化。层次取两个因素Ci和Cj，用Cij表示性能指标Ci和Cj对电池性能的重要性程度之比，全部比较结果可用比较矩阵A表示。A=（Cij）m×n，Cij> 0，Cij= 1/Cji。为了从判断矩阵中提炼出有用的信息，达到对事物的规律性认识，就需要通过两两对比按照重要性等级赋值，然后计算每个判断矩阵的权重向量，从而完成从定性分析到定量分析的过度，这是层次分析法的第二个基本特征。表 1 中，Cij赋值这些数字是根据人们定性分析的直觉和判断力而定的，表示重要度等级，介于Cij= {1,3,5,7,9,1/3,1/5,1/7,1/9} 重要度等级赋值的可以用Cij= {2,4,6,8,1/2,1/4,1/6,1/8} 赋值。

表1 判断矩阵标度 1–9 尺度及 Cij 的含义[2]

1.4 层次单排序及其一致性检验

判断矩阵A的特征根问题AW=λmaxW的解W，经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值，这一过程为层次单排序[3]。为了能用矩阵A的对应特征根λ的特征向量W作为被比较的权向量，需要进行一致性检验。当n= 1,2 时，A总为一致阵；当n> 3 时，如果CR=CI/RI＜0.1，则可以认为A的一致性程度在允许范围之内，其特征向量可用作为权向量，否则需要重新比较。注：W为所求的特征向量；λmax为最大特征根；n为阶数，CI= (λmax-n)/(n- 1)；CI为矩阵A不一致程度的指标；CR为矩阵A随机一致性比率，CR=CI/RI；RI为 1–9 阶矩阵的平均随机一致性指标（见表 2）。

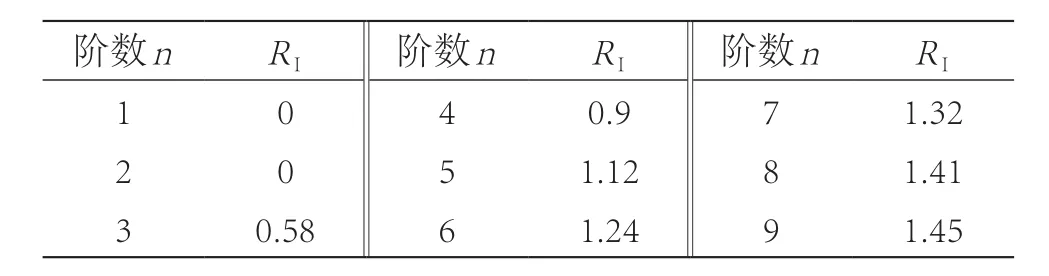
表2 矩阵的随机一致性指标[2]

1.5 层次总排序

系统中各层元素对总目标的合成权重的计算：通过判断矩阵，计算准则层对目标层的权向量W1；通过方案层中两两比较，计算方案层对准则层的权向量W2；由方案层对目标层的权向量W3=W2W1，进行总排序，来确定系统中最底层各个元素在总目标中的重要程度[3]。

1.6 相应的决策

通过W3的计算结果，寻找最优供应商。

2 实例验证

2.1 明确问题

从甲、乙、丙、丁四个厂家各购买了 14 只 45 Ah电池，通过 9 个试验项目的测试，系统评估各家电池的优势和劣势，总目标为从中选择性价比最好的电池。

2.2 建立层次结构

先将蓄电池综合评价模型分为 3 个层次：最上层为目标层，即最优供应商；最下层为方案层，即4 个可选供应商；中间层为指标层，即本项目中的检测项目（包括容量、-18 ℃ 低温起动能力、荷电保持能力、耐振动性能、循环耐久能力、水损耗等指标）。各层次间的联系用相连的直线表示，见图2。通过判断矩阵得出指标层间的权重，通过指标层的测试结果比对得到方案层的权重，根据指标层和方案层综合评价目标层的权重，确定蓄电池性能指数。根据性价比的定义，将蓄电池的价格进行归一化处理，最后求出电池的性价比，得出最优供应商。

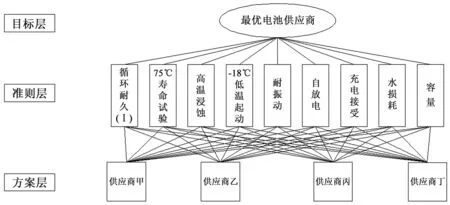
图2 电池供应商评价层次分析法结构示意图

2.3 构造判断矩阵

判断矩阵标度 1–9 尺度对应的因素有 9 个。表 3 中：C1表示循环耐久(I)；C2表示 75 ℃ 循环寿命；C3表示高温侵蚀；C4表示 -18 ℃ 低温起动能力；C5表示耐振动性能；C6表示自放电；C7表示充电接受能力；C8表示水损耗；C9表示容量。

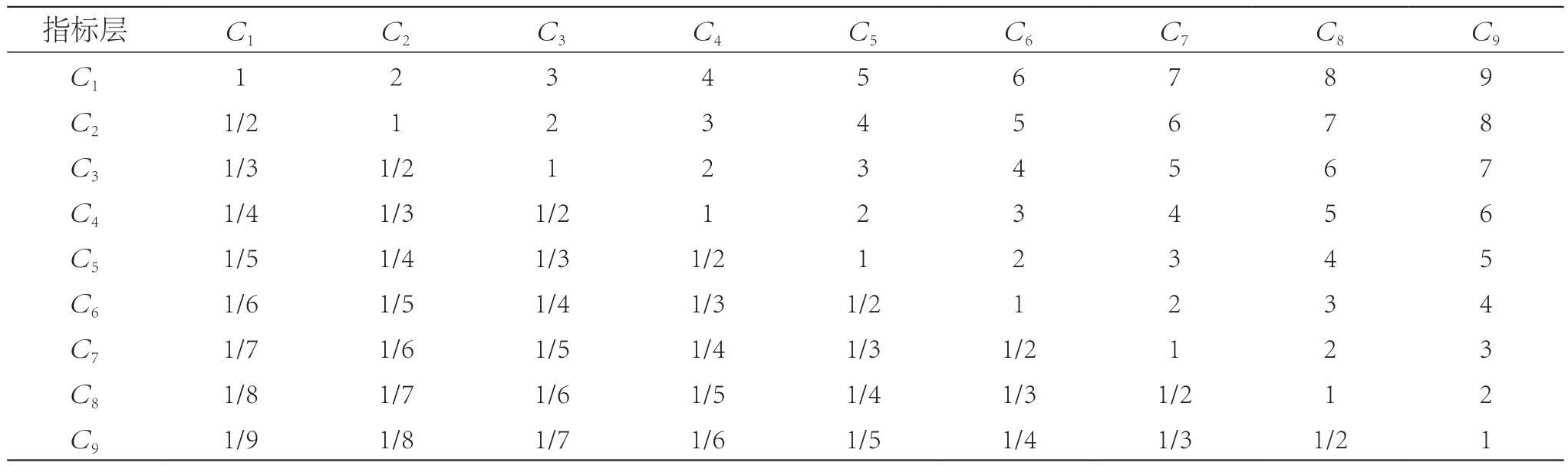
表3 电池测试项目判断矩阵

2.4 层次单排序及其一致性检验

通过计算得到，一致性指数CR= 0.0345，最大特征根λmax= 9.4005，CI= 0.0501，RI= 1.45。由于CR=CI/RI= 0.0501/1.45＜0.1，A的不一致性程度在允许范围之内，所以可用其归一化特征向量可作为权向量[4]（见表 4）。指标层相对于目标层的权向量：W1= (0.308119, 0.223483, 0.156995, 0.108415,0.074296, 0.050914, 0.035159，0.024699, 0.017914)T。W1权向量的计算由 DPS 数据处理系统软件计算得来；T为该向量矩阵的转置矩阵。将指标层电池性能的重要性进行单项排序：C1＞C2＞C3＞C4＞C5＞C6＞C7＞C8＞C9。

表4 方案层间的权向量

2.5 层次总排序

在构造第 3 层方案层对第 2 层指标层的各性能指标的成对比较矩阵时，可直接根据各指标的测试结果进行两两比较来构造矩阵，即B= (bij)m×n式中bij为方案Pi与Pj中各指标的测试结果比值。先求出权向量W2= (W甲，W乙，W丙，W丁)。W2权向量的计算，由各厂家方案层各测试指标均值的比值归一化处理得来，具体见表 5。再求出方案层相对于目标层的组合向量W3=W2W1= (0.226237 0.297682 0.213761 0.262418)。

表5 供应商电池市场价格归一化处理

2.6 根据计算结果，考虑相应的决策

由价格工程理论构建的性价比模型，性价比APRI 指标就等于A/V=（性能指数A/价格指数V）×100 %。其中：A为W3向量，V为四个供应商市场价归一化处理后的向量。甲的 APRI 是 A/V =(0.226237/0.2477) ×100 % = 91.34 %；乙的 APRI 是A/V = (0.297682/0.2068) × 100 % = 143.95 %；丙的 APRI是 A/V = (0.213761/0.2809) ×100 % = 76.10 %；丁的APRI 是 A/V = (0.262418/0.2647) ×100 % = 99.14%。因此按性价比 APRI 排序就是：乙＞丁＞甲＞丙。

3 结论

在本文中，笔者运用层次分析法构建了以电池产品质量性能为基础的供应商评价体系，将电池检测中的各个性能指标有机结合起来，将人们的思维过程数学化、模型化、系统化、规范化，便于人们接受，并且建立了性价比模型，把性能指标和价格指标综合起来，通过计算得出供应商甲的性价比最高。

通过本项目可以看出，层次分析法能把一个多指标多厂家的复杂评价问题表示为有序的递阶层次结构，这种方法能够统一处理决策中的定性和定量因素，具有系统性、实用性、简明性等优点[5]。但是，这种评价方法也有不足之处，就是他完全依靠主观分析做出指标层间各性能指标的权重判断，受主观影响较大。